无人艇动稳性试验与数值验证

冯月卫，王 辉，周 杰

(1.南通中远川崎船舶工程有限公司，江苏 南通226000;2.哈尔滨工程大学，黑龙江 哈尔滨150001)

0 引 言

21世纪是一个竞争的世纪，人类利益争夺的触角已经投向遥远的太空、宇宙以及广阔的海洋。其中海洋所蕴藏的巨大经济利益以及在政治上的重要地位，使得各国对海洋权利的争夺日趋激烈［1］。在信息科技革命中新兴的各种智能化设备是人们借以征服海洋的利器，而处在最前沿的依然是智能化武备。本文要研究的对象就是这样一种自主航行并执行各种任务的水面航行器——无人艇(USV)［2］。

无人艇在军事领域的应用涉及到情报、侦察和监视(ISR)、水雷战、反潜战、反舰战、力量保护、港口安全、精确打击、海上拦截和封锁、特种作战支持等。各国海军对于无人艇的一系列前沿应用表现出越来越浓厚的兴趣，无人艇研究项目持续推进，新船型应用逐渐增多，自主性不断提高。

无人艇的动稳性是一个重要的性能指标［3］。国内外关于滑行艇动稳性的研究和实验很少，尚未形成可以参考的理论成果。在无人艇动稳性方面展开研究和试验是具有开创性和挑战性的一个方向。

1 模型试验

关于滑行表面的水动力计算研究起源于20世纪40年代NACA 在兰利的拖曳实验［4］，基于这些实验后续的许多相关研究才得以展开。无人艇的水动力系数具有非线性，要准确确定这些水动力系数可靠的方法是通过模型试验获得。无人艇模型试验主要测量高速航行横倾的航行姿态，横向恢复力和力矩。期望通过调整、确定无人艇部分参数，建立参数对稳性、抗倾覆性能、浮态恢复效果的数学关系模型，为布局优化提供支撑和参考。对于高速横倾航行的船舶模型试验，据目前资料显示，类似的试验只有英国南安普顿大学的水池实验室做过，如图1所示，该研究横倾航行的船舶模型试验主要用于帆船的设计。对于高速航行横倾时滑行艇水动力系数测量的模型试验，难度系数更高，此试验在国内尚属首次，在试验装置的设计和试验方案的确定等方面都是试验的困难所在。

图1 Wolfson Unit模型试验图Fig.1 Model test of Wolfson Unit

1.1 试验方案

本试验中滑行艇试验模型与实船的比例关系为1∶2.5，主要对滑行艇的强迫横倾进行试验研究，试验是在中国特种飞行器设计研究所的高速拖曳水池进行的。该试验模型的主要参数如下:

模型如图2所示。

图2 无人艇试验模型Fig.2 Experimental model of USV

在本试验中需要固定无人艇模型横向角度，保持其他方向自由度自由运动，以傅汝德换算速度拖曳模型，测量相应状态的恢复力矩，同时测量纵倾角、升沉。试验测量几个不同角度的相应数值。为了保证实现该功能，设计了横倾固定的辅助试验装置，如图3所示。该装置由以下几部分构成:横倾角固定装置、导杆装置、滑杆装置、砝码。横倾角固定装置保证了固定横倾角状态;导杆和滑杆装置实现了垂向的无约束滑动;砝码是为了抵消装置自身重力对于试验的影响。

图3 横倾固定装置与安装图Fig.3 Heeling fixtures and installation drawing

试验主要由2 部分组成:试验可靠性验证和固定横倾角高速直航试验。试验可靠性验证是对比固定横倾角装置与传统拖线方式2 种情况下测量的无横倾角直航状态下的航态参数，以说明本试验装置的测量数据的可靠性程度。

1.2 试验可靠性验证

由于本试验是首次使用自行设计的横倾固定装置对无人艇的阻力、纵倾角、升沉、恢复力矩等数据进行测量，为验证这些试验数据的可靠性，在此之前先进行正常拖曳式阻力试验，通过对比得到固定横倾装置试验数据的可靠性程度。

表1 设计装置与拖线方式试验数据Tab.1 Experiment data of design device and towing method

图4 阻力曲线对比Fig.4 Resistance curve contrast

图5 纵倾角曲线对比Fig.5 Trim Angle curve contrast

图6 升沉曲线对比Fig.6 Heave curve contrast

从拖线式船模阻力试验和固定横倾装置阻力试验2 组数据对比中可以得到，纵倾角和升沉除了在个别点之外，整体趋势和测量数值都是十分吻合的，数据可信。阻力值在变化趋势上是相同的，整体误差在11%左右，需要对数据进行一定的处理之后才能进一步使用。阻力值在测量上存在误差可能是由以下原因造成的:六分力天平量程过大(300kgf)引起的精度损失;直航过程中在套杆处产生的惯性力引起的滑动摩擦力增大。

1.3 固定横倾角高速直航试验

试验中无人艇固定横倾角实际测量值分别为4.5°，11°，18°，试验结果见表2、表3和表4。

2 试验数值验证

本节采用Fluent 软件对横倾试验进行数值模拟，并将计算值和试验值进行对比。试验中无人艇固定横倾角实际测量值分别为4.5°，11°，18°，在本节中对横倾角为4.5°，11°，18°的滑行艇在航速为2 m/s，4 m/s，6 m/s，8 m/s 时的情况进行模拟，共计12 种工况。

2.1 计算模型

计算模型的尺寸和试验船模的尺寸比例为1∶1。图7为采用Gambit 软件建立的该滑行艇三维计算模型。

图7 滑行艇三维计算模型Fig.7 Three-dimensional calculation model of USV

2.2 计算域的选取及边界条件的设置

计算域后端距艇尾11 m，前端距艇首5.5 m，底部距艇底3.6 m，侧面距艇中4 m，顶部距甲板1.9 m。其边界条件为:计算域右端为速度入口，计算域左端为压力出口，其余边界条件为壁面边界条件。

2.3 网格的划分

如何生成高品质的计算网格是CFD的一个重要课题［5］，划分网格是建立计算模型中难度最大的部分，网格单元划分的好坏不仅决定了能否得到正确解，还决定了求解时间的长短［6－7］。由于计算域范围较大，而计算主要关心的滑行艇附近的流场，所以滑行艇附近网格较密，远离滑行艇的计算区域逐渐变疏，但要注意网格疏密过渡时的连续性。在本文中网格的划分采用如下方法:先在滑行艇周围建立一个小域包围滑行艇，并将滑行艇分成前后2 部分，前面部分适当加密，用以模拟滑行艇船首飞溅，由于艇体艇型较复杂，所以其表面全采用三角形网格，如图8所示;小域内采用的是四面体的非结构化网格;计算域的其他地方都采用的是六面体结构化网格，网格划分如图9所示。

图8 艇体表面网格Fig.8 The hull surface grid of USV

图9 网格划分Fig.9 Meshing of calculation area

2.4 数值模拟结果

表2、表3和表4为试验值与计算值的对比。

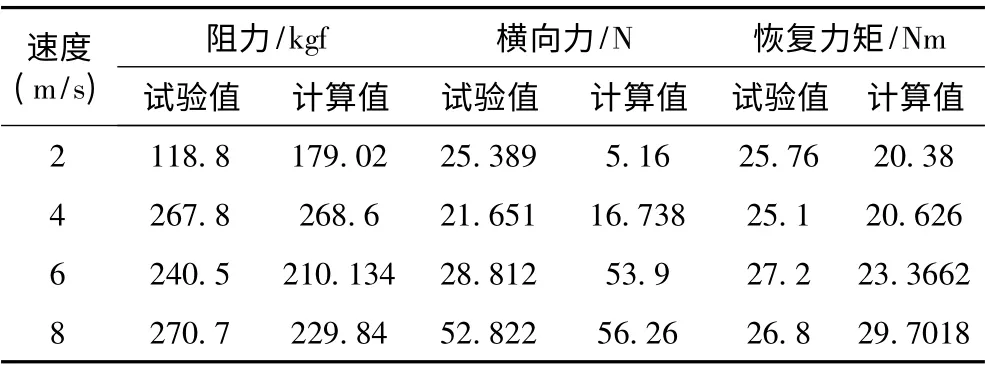
表2 横倾角为4.5°Tab.2 Heeling Angle is 4.5°

表3 横倾角为11°Tab.3 Heeling Angle is 11°

表4 横倾角为18°Tab.4 Heeling Angle is 18°

3 结 语

设计了无人艇横倾直航试验并验证了试验装置的可靠性。测量了横倾角为4.5°，11°，18°时的阻力、横向力、恢复力矩等水动力参数，并且采用Fluent 软件对其中的12 种工况进行了数值模拟，数值结果与试验结果符合度较好。数值计算方法能为船模试验提供技术参考，为布局优化问题的进一步探索提供了有利依据。

［1］徐玉如，苏玉民，庞永杰.海洋空间智能无人运载器技术发展展望［J］.中国舰船研究，2006，3(1):1673－3185 XU Yu-ru，SU Yu-min，PANG Yong-jie.Expectation of the development in the technology on ocean space intelligent unmanned vehicles［J］.Chinese Journal of Ship Research，2006，1(3):1673－3185.

［2］谢毅.水面无人艇抗倾覆系统分析及仿真研究［D］.哈尔滨:哈尔滨工程大学，2008.XIE Yi.The study on USV anti-sunk system analysis and simulation［D］.Harbin:Harbin Engineering University，2008.

［3］刘维华.无人艇稳性及浮态恢复性能研究［D］.哈尔滨:哈尔滨工程大学，2011.LIU Wei-hua.The study on USV performance about stability and float capability ［D］.Harbin:Harbin Engineering University，2011.

［4］CHAMBLISS D B，BOYD G M.The planning characteristics of two V-shaped prismatic surfaces having angles of deadrise of 20° and 40° ［R］.Langley Aeronautical Laboratory，NACA.Tech .Note 2876.Washington，1953.

［5］MARVIN J G.Perspective on Computational Fluid Dynamics Validation［J］.AIAA Journal，1995.

［6］常煜，张志荣，赵峰.多块结构化网格在含附体水面船模粘性流场数值计算中的应用［J］.船舶力学，2004，8(1):19－25.CHANG Yu，ZHANG Zhi-rong，ZHAO Feng.Application of multi-block structured grid to computation of viscous flow around a ship with appendage［J］.Journal of ship mechanics，2004，8(1):19－25.

［7］张怀新，刘应中，缪国平.带自由面三维船体周围粘性流场的数值模拟［J］.上海:上海交通大学学报，2001，35(10):1429－1432.ZHANG Huai-xin，LIU Ying-zhong，MIAO Guo-ping.Numerical simulation of three-dimensional viscous flow with free surface about a ship［J］.Journal of Shanghai Jiaotong University，2001，35(10):1429－1432..