对转导管螺旋桨的水动力设计与分析
2014-12-07周军伟倪豪良
周军伟,倪豪良
(哈尔滨工业大学(威海)船舶与海洋工程学院,山东 威海264209)
0 引 言
为适应高速、高推力情况对船舶推进器性能的要求,采用对转螺旋桨是一种选择,这是因为对转螺旋桨能够减小甚至消除尾流中的旋流,提高推力系数;采用导管螺旋桨是另外一种选择,它同时具有高效率、高推力和低噪音的优点。结合对转螺旋桨和导管螺旋桨的特点,可以构造出对转导管螺旋桨,有可能进一步提高推进器的性能。
对转螺旋桨的结构相比传统螺旋桨要复杂的多,其结构形式主要有套轴结构、吊舱结构与双驱动结构形式[1]。这3 种结构都能够与导管配合,构成对转导管螺旋桨,如图1所示。随着叶环电力驱动导管螺旋桨技术的发展[2-5],对转导管螺旋桨的结构能够变得更为简单,也使船舶采用对转导管螺旋桨作为推进器逐渐成为可能。
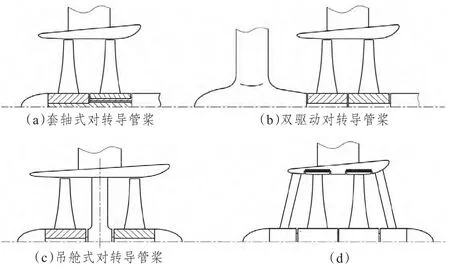
图1 对转导管螺旋桨的几种可行的结构形式Fig.1 Several feasible structures of contra-rotating ducted propeller
水动力设计是对转导管螺旋桨设计中的关键问题之一。虽然以往也有许多针对对转螺旋桨水动力性能的 研究,如Yang与Davide 等[7-8]基于升力面法对对转螺旋桨的定常性能预报,Zhang与王展智等[9-10]对对转螺旋桨流场的CFD 模拟,但仍然没有一个较为方便的对转螺旋桨水动力设计方法,就更不要提对转导管螺旋桨的水动力设计了。
本文基于叶栅理论提出一种对转导管螺旋桨中对转转子的设计方法,并基于现有的Ka4-55 系列螺旋桨设计1 部对转导管螺旋桨。其导管在现有的19A 导管翼型上略做改动,以满足对转转子对导管长度的要求。
1 对转转子的叶栅理论
导管螺旋桨的转子工作在导管形成的管道内,因而可认为是工作在内流环境中。因为在内流环境中,螺旋桨桨盘使管道内流动增压,但不能改变桨盘前后轴向速度。忽略导管内流动的旋流成分,则可以用激盘模型来模拟桨盘的工作状态,如图2所示。激盘前后参数满足关系
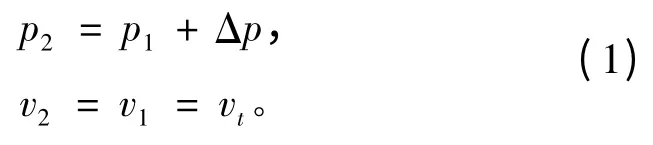
式中:Δp为桨盘压升;vt为喉部轴向速度。
从导管流动的激盘模型可看出,改变激盘的压升Δp 能够改变喉部轴向速度vt,这2个参数之间的关系仅与导管的几何相关。根据导管几何确定合适的Δp与vt后,可依此进行对转转子的设计。Δp与vt的确定方法与对转转子的设计无关。

图2 导管/激盘模型Fig.2 The duct/actuator-disc model
1.1 压升与速度的关系
对转导管桨在工作过程中,第一级转子对流动做功,根据动量矩定理,其尾流中必然存在一定的旋流;第二级转子反向旋转,因而其对流动施加一个反向旋转的的作用。在理想状态下,对转转子能够保证其尾流中不存在旋流。对转转子的速度三角形如图3所示,图中,ΔVθ为二级转子中间旋流在绝对坐标系下的周向速度分量,U为当地半径处翼型的切向运动速度。图中1,2,3 分别表示第一级转子前、二级转子中间和第二级转子后的3个位置,1.5与2.5 分别表示第一级和第二级转子的中间位置。

图3 对转转子的速度三角形Fig.3 Velocity triangle of the contra-rotating rotors
根据动量矩定理,并假设螺旋桨转子内流线都沿圆柱面,即流线经过转子后半径不变,则螺旋桨转子总压升ΔPt与动量矩的关系可表示为

对于第一级转子而言,由于尾流中的旋流会导致静压下降,所以第一级转子静压升为
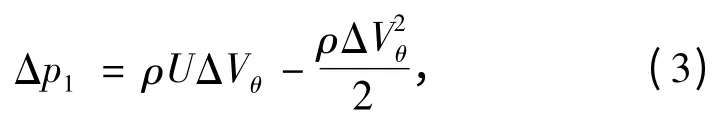
第二级转子由于回收了第一级转子尾流中的旋流损失,因而产生的压升要高于第一级
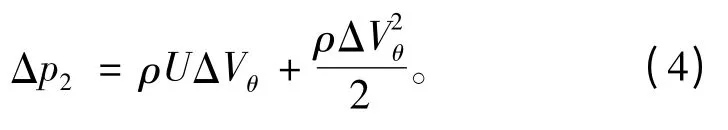
1.2 速度与转子几何的关系
根据导管喉部轴向速度Vt和二级转子中间旋流切线速度ΔVθ可确定螺旋桨对转转子的水动力螺距角。二级转子的相对进出口水动力螺距角分别表示为

式中:角度下标分别对应图3 中的位置标示,其中21,22 分别表示在第一级与第二级转子的相对转动坐标系下。
根据叶栅实验研究,水动力螺距角与几何螺距角之间总是存在一定的差值Δθ,即滑脱角。滑脱角主要与翼型及螺旋桨盘面比相关。在已知所选用翼型及盘面比的情况下,可确定不同半径处的滑脱角,进而得出桨叶的几何螺距角为

2 对转导管螺旋桨的设计
本文中的对转导管螺旋桨是在已有单转子导管螺旋桨19A/Ka4-55的基础上发展而来的。二者采用同样的翼型、盘面比与导管翼型,而螺距角分布则根据上一节中对转转子的水动力原理重新设计。为了便于二者对比,单转子导管螺旋桨的转子采用对转转子的第一级替换。
2.1 导管设计
单转子导管螺旋桨仍采用原有的19A 导管翼型,如图4所示。对转转子由于轴向长度增加,因而必须增加导管长度以保证能够容纳2个转子。将19A 导管的内壁面从0.5 弦长位置截断,分别向前后移动0.25 弦长;而后,在保证前后缘导圆的情况下用直线连接导管外壁面,得到新的加长导管(定义为19AL),作为对转导管螺旋桨的导管。

图4 19A 导管与加长后得到的19AL 导管Fig.4 The 19A duct and the lengthened 19AL duct
2.2 转子设计
对转导管螺旋桨的初步设计要求如表1所示。

表1 对转转子的设计参数Tab.1 The design parameters of the contra-rotating rotors
根据前期对19A与19AL 导管的分析,当喉部速度与来流速度之比在1.4 左右时,导管螺旋桨能够达到最高效率,因而本文选取导管喉部速度Vt=20 m/s。
根据推力系数要求,可得第一级转子前后压差近似为
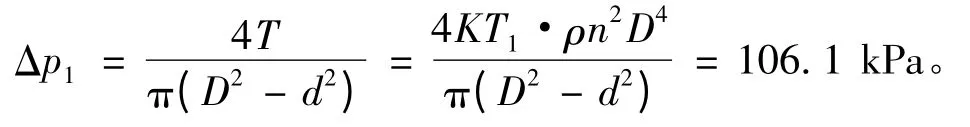
从式(3)~式(4)可看出,同样的压升要求,当处于较小的半径位置时,由于切线速度U 变小,因而需要较大的ΔVθ;在U 非常小的情况下,ΔVθ无解。为了避免这种情况出现,本文适当降低轮毂附近桨叶压升。实际设计中不同半径处的压升如图5所示。已知压升,根据式(3)~式(5)可 得 不 同 半 径 处ΔVθ,θ1,θ21,θ22,θ3,如表2所示。
根据前期对导管螺旋桨19A/Ka4-55的流场分析发现,在不同进速系数下,该螺旋桨桨叶的滑脱角沿半径的分布曲线几乎一样。图6 给出了本文中采用的滑脱角沿半径的分布曲线。采用Ka 系列翼型,得到盘面比为0.55的4 叶对转导管桨和单转子导管桨如图7所示。
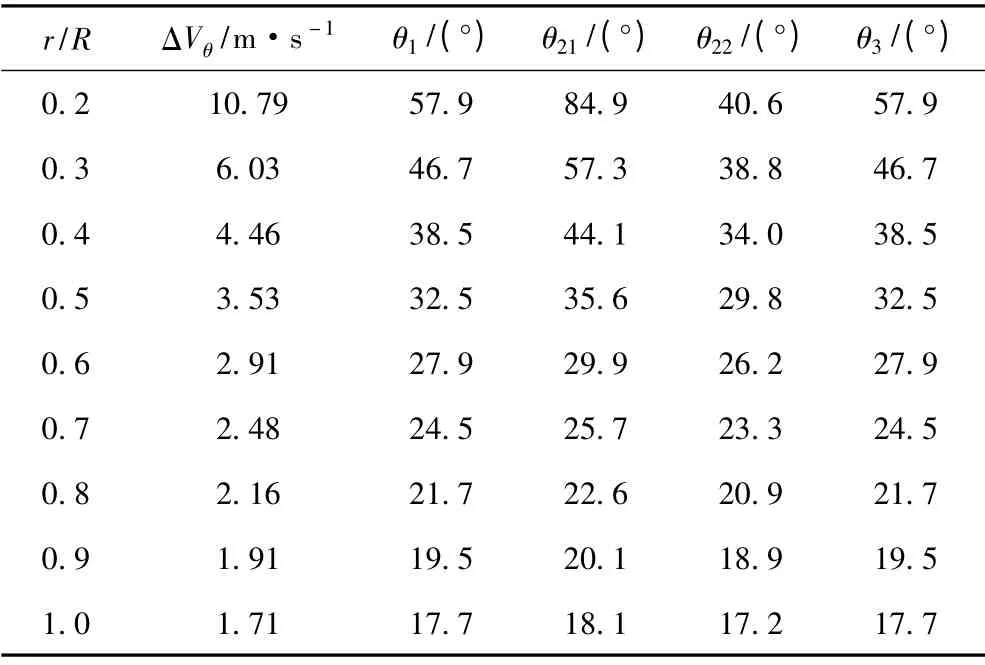
表2 不同半径处的水动力参数Tab.2 The hydrodynamic parameters at different radius
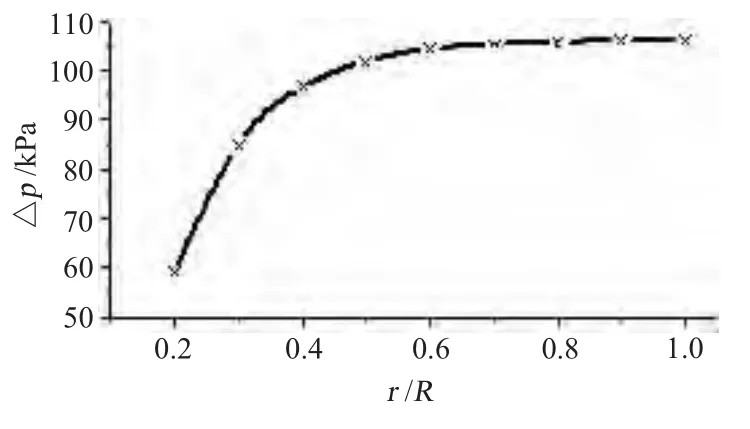
图5 不同半径处的设计压升Fig.5 The designed pressure rise at different radius

图6 Ka4-55 导管桨滑脱角沿半径的分布曲线Fig.6 The slip angle of the ducted propeller Ka4-55 at different radius

图7 单转子导管桨与对转导管桨的外观Fig.7 Views of the single rotor ducted propeller and the contra-rotating ducted propeller
3 数值方法
采用适用的商用软件CFX[11-12]对单转子导管螺旋桨和对转导管螺旋桨的流场进行求解。计算中仅对1/4 流域进行求解,以节约计算时间。单转子导管桨的流域划分为静止域与转动域,分别在静止坐标系和转动坐标系下进行求解;转静交界面采用Frozen Roter 转静边界条件连接。由于流动近似为定常,因此采用定常求解方法。对转导管桨的流域划分为静止域、第一级转子的转动域与第二级转子的转动域,分别在各自的坐标系下进行求解;前后2 组转静交界面采用Frozen Rotor转静边界条件,二级转子之间的转静交界面采用Transient Rotor Stator 转静边界条件;由于不同时刻二级转子间的干扰情况不同,因而采用非定常的求解方法。
对转导管螺旋桨的网格与边界条件分别如图8与图9所示。由于单转子导管桨与对转导管桨具有类似的几何,其网格与边界条件不重复介绍。二者的进口都给定轴向来流速度,出口给定静压条件。数值方法已经在以往的工作中得到校验[13]。
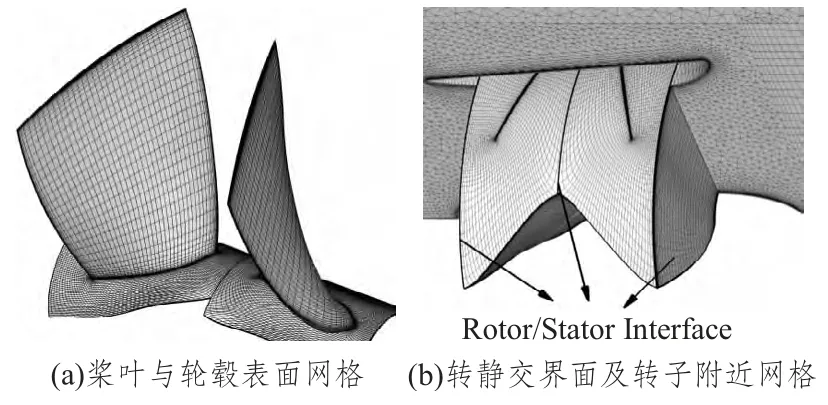
图8 对转导管桨的网格与流域划分Fig.8 Mesh and flow region divide of the contra-rotating ducted propeller

图9 对转导管桨流域网格与边界条件Fig.9 Mesh of far field and the boundary condition around the contra-rotating ducted propeller
4 结果与分析
4.1 性能对比
图10 中对比了单转子导管桨与对转导管桨的性能曲线。图中SR 表示单转子,CR 表示对转转子。可以看出,不论推力还是扭矩,对转导管桨都要高于单转子导管桨。对比总推力系数KT与导管推力系数KTn 可以看出,二者的总推力系数KT 相差较大,而导管推力系数KTn 相差较小,这表明对转转子的压升要大于单转子。二者的效率曲线非常接近,其最高效率点都出现在J=0.7 附近,但对转导管桨的最高效率比单转子导管桨低了大约3%。为了探索对转导管桨效率降低的原因,以下将分析对转转子内的流动情况。
图11 给出了对转导管桨在J =0.7 时第一级转子与第二级转子尾流中切向速度周向平均值的分布曲线,分别用下标2和3 表示。可以看出,第二级转子尾流中的切向速度分量明显小于第一级,这说明第二级转子的确能够回收第一级转子尾流中的大部分旋流损失。在尾流中旋流损失回收的情况下,对转导管桨的效率仍然降低,可以推断,第二级转子的桨叶表面摩擦损失大于所回收的尾流中的旋流损失。

图10 单转子导管桨与对转导管桨的性能曲线Fig.10 Performance curves of the single rotor and the contra-rotating ducted propeller

图11 J=0.7 时对转导管桨两级之间及出口位置的周向速度分布曲线Fig.11 Tangential velocity at different radius of position 2 and 3 at J=0.7
4.2 设计参数校验
1)单转子导管桨
图12 中给出了单转子导管桨在3个进速系数下不同截面位置处轴向速度沿半径方向的分布曲线。速度下标1,1.5,2 分别表示桨盘前、桨盘中间和桨盘后截面位置。从图3 中第一级转子的位置标示可以看出,在进速系数J=0.7 时,桨盘后位置轴向速度与喉部设计速度十分接近。随着进速系数的降低,桨盘负荷增大,为了产生较大攻角,轴向速度降低,反之则提高。
在桨盘前位置,由于流道截面积增大,所以轴向速度略低。在靠近导管内壁附近的区域,由于导管存在曲率,所以有流动加速现象。这种流动加速现象十分明显,以进速系数J =0.7 时为例,轮毂附近轴向速度比约为0.95,而在导管内壁附近,轴向速度比可达1.1。导管的这种加速效应会影响转子的设计,即实际中喉部速度沿半径的分布并非常值,在转子的优化设计中必须予以考虑。
图13 给出了3个进速系数下单转子导管桨桨盘前及桨盘后旋流分量的分布曲线。可以看出,桨盘前旋流分量几乎为0,而桨盘后旋流分量随进速系数的降低而增大。根据式(2)不难理解,在较低的进速系数下,螺旋桨转子做功更多,根据动量定理,其旋流分量必然增大。

图12 不同进速系数下单转子导管桨3个位置的轴向速度分布曲线Fig.12 Axial velocity at different radius of position 1,1.5 and 2 at different advanced coefficient
2)对转导管桨
图14 给出了进速系数J =0.4与J =0.7 两种情况下截面位置2,3的轴向速度分布曲线。从图中可看出,与单转子相比,对转转子的实际轴向速度明显大于设计喉部速度。从图10 中的性能曲线对比来看,在J=0.7 时,对转导管桨的推力系数明显大于单转子导管桨,而二者在导管上的推力相差很小,这表明对转转子压升要大于单转子,即对转转子激盘模型的前后压差更大,因而其轴向速度更大。

图13 不同进速系数下单转子导管桨进出口的周向速度分布曲线Fig.13 Tangential velocity at different radius of position 1 and 2 in the single rotor ducted propeller at different advanced coefficient

图14 不同进速系数下对转转子间及出口位置的轴向速度分布曲线Fig.14 Axial velocity at different radius of position 2 and 3 in the contra-rotating rotors at different advanced coefficient
4.3 对转转子间的匹配
图15 给出了对转转子的推力系数和扭矩系数的对比。可以看出,第一级转子的推力系数与扭矩系数随进速系数的变化都要平缓的多,而第二级的则对进速系数更为敏感。对转转子的等扭矩大致出现在J=0.43的位置,此时第一级转子的推力小于第二级,这与式(3)和式(4)中描述的一致。对转转子等扭矩点位置的推力系数并没有达到设计的0.2,这是由于设计中降低了轮毂附近的压升值。

图15 对转转子的推力与扭矩对比Fig.15 Comparison of thrust and torque of the contra-rotating rotors
由于对转的2个转子之间的相位在不断发生变化,其受力也必然随时间变化。图16 给出了J=0.7与J =0.4 两个进速系数下对转转子推力、扭矩与导管推力随时间的变化。可以看出,对转转子的推力与扭矩脉动几乎总是同相位。尽管在不同进速系数下二者推力与扭矩脉动的平均值发生变化,但脉动幅度基本不变。推力系数的脉动幅度约为ΔKT =0.04,扭矩系数的脉动幅度约为ΔKQ =0.007。在今后的设计中,可以考虑通过改变对转转子的叶片数来降低推力与扭矩的脉动量。
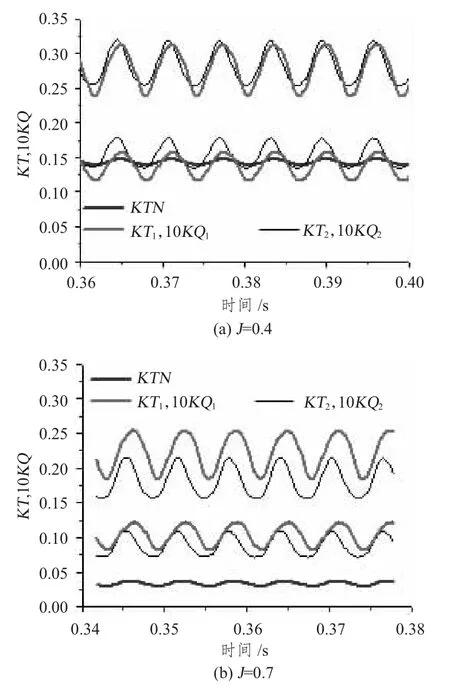
图16 不同进速系数下对转导管桨桨叶与导管的受力脉动Fig.16 Thrust and torque fluctuation of the contra-rotating rotors and the duct at different advanced coefficient
5 结 语
本文基于叶栅理论初步设计了1 部对转导管螺旋桨。同时将对转导管桨的第一级转子单独与导管配合,构造了1 台单转子导管桨,用于与对转导管桨进行对比。采用CFD 方法得到了2个导管桨的性能曲线与流场特征,分析发现:
1)2个导管桨的最佳效率点几乎在同样的进速系数下,由此可见导管桨的效率曲线受转子的影响较小,主要与导管几何相关;
2)对转导管桨的推力与扭矩较单转子导管桨的高,但效率略低;分析发现,对转导管桨的确能够削弱尾流中的旋流,因而推断:对转导管桨效率降低的主要原因是对转转子增加了叶片表面摩擦损失;
3)按照叶栅理论设计的桨叶,其性能基本能够与设计值符合;在对转导管桨中,为了实现设计推力,其设计点向左偏移,并不在最高效率点位置,这是因为文中没有考虑对转转子与导管的匹配。
4)从对转转子之间的匹配性来看,对转转子中第一级转子的推力和扭矩随进速系数的改变较为平缓,第二级转子反之;二者的推力与扭矩脉动幅度相当,且在不同进速系数下其脉动幅度基本不发生变化。
[1]聂延生,韩学胜,曾鸿,等.对转螺旋桨的结构原理及特点分析[J].船电技术,2005(2):50-52.NIE Yan-sheng,HAN Xue-sheng,ZENG Hong,et al.Analysis about the construction principle and characteristics of contra rotating propeller [J].Marine Electric &Electronic Engineering,2005(2):50-52.
[2]沈武铮.全回 转导管型对转桨推进装置[P].专利,2010.SHEN Wu-zheng.Gyration ducted contra-rotating propeller propulsion system[P].Patent,2010.
[3]TAYLOR O S,REPP J R,BROWN D W.Submersible electric propulsion motor with propeller integrated concentrically with motor rotor[P].US Patents,1989,4831297 A.
[4]DINE P V,FRANCO A,et al.Rim-driven propulsion pod arrangement[P].US Patents,2005,6837757 B2.
[5]SHU Hau-lai.Design optimisation of a slotless brushless permanent magnet DC motor with helically-wound laminations for underwater rim-driven thrusters [D].Doctoral Thesis,University of Southampton,2006.
[6]曹庆明,洪方文,胡芳琳.梢部驱动推进器的研究与进展[C]//第九届全国水动力学学术会议暨第二十二届全国水动力学研讨会文集,2009.CAO Qing-ming,HONG Fang-wen,HU Fang-ling.Research and development of rim-driven propeller[C]//Proceedings of the 22nd National Conference on Hydrodynamics,2009.
[7]YANG C J,TAMASHIMA M,et al.Prediction of the steady performance of contra-rotating propellers by lifting surface theory[J].Transactions of the West-Japan Society of Naval Architects,1991(82):17-31.
[8]GRASSI D,BRIZZOLARA S,VIVIANI M,et al.Design and analysis of counter-rotating propellers-comparison of numerical and experimental results [J].Journal of Hydrodynamics,2010,22(5):570-576.
[9]ZHANG Tao,YANG Chen-jun,SONG Bao-wei,et al.CFD simulation of the unsteady performance of contra-rotating propellers[J].Journal of Ship Mechanics,2011,15(6):605-615.
[10]王展智,熊鹰,齐万江.对转螺旋桨敞水性能数值预报[J].华中科技大学学报(自然科学版),2012,40(11):77-88.WANG Zhan-zhi,XIONG Ying,QI Wan-jiang.Numerical prediction of contra-rotating propellers' open water performance[J].Journal of Huazhong University of Science and Technology (Nature Science Edition),2012,40(11):77-88.
[11]LONG Yu,GREVE M,DRUCKENBROD M,et al.Numerical analysis of ducted propeller performance under open water test condition[J].Journal of Marine Science and Technology,2013,18(3):381-394.
[12]CAO Qing-ming,HONG Fang-wen,TANG Deng-hai,et al.Prediction of loading distribution and hydrodynamic measurements for propeller blades in a rim driven thruster[J].Journal of Hydrodynamics,2012,24(1):50-57.
[13]周军伟,王大政.导管螺旋桨不同桨叶的叶梢泄露涡分析[J].哈尔滨工业大学学报,2014,46(7):14-19.ZHOU Jun-wei,WANG Da-zheng.Analysis of tip leakage vortex of different blade in ducted propeller[J].Journal of Harbin Institute of Technology,2014,46(7):14-19.
