基于局部应力应变Neuber法的舵板寿命分析

郑帮涛，马 永

(1.海军装备部，北京100161;2.中国船舶重工集团公司 第七一三研究所，河南 郑州450015)

0 引 言

舵板是训练模拟系统的重要组成部分，通过流体驱动实现展开动作，进而使弹体产生横向推力，实现水平位移。当舵板展开至极限位置时，舵板结构会产生很大的冲击应力及应变。出于安全性考虑，需要评估舵板在多次过载冲击后的剩余寿命。

对于高周、低应力(弹性范围)疲劳问题，尽管国际上已研究了相当长时间，但目前仍主要以实测为主，采用基于名义应力的雨流技术法和疲劳累积损伤理论进行寿命预测，以有限元仿真和理论模型预测为辅［1－2］。从已发表的相关文献看，目前的理论预测精度与实测仍有较大差距，不能完全替代实验［3］。对小能量冲击疲劳问题［4］，在我国20世纪60－70年代有研究，主要采用专门的摆锤冲击实验;对于大能量多次冲击的研究尚未发现有关技术资料。课题所涉及的问题属于多次间歇性过载冲击下的疲劳寿命预估问题。既不同于高周、低应力、交变或脉动载荷下的疲劳问题，也不同于低周、低应力、小能量冲击载荷下的冲击疲劳问题，本课题在每次冲击中都可能包括塑性变形和残余应力，且总的寿命(次数)也远远小于通常意义的“疲劳”寿命。

本文在借鉴传统高周、低应力疲劳理论预测和低能量冲击实验基础上，开展了材料的循环应力应变试验，基于静态拉伸试验数据估算了材料的疲劳寿命参数，给出了几种材料应变寿命曲线估算及修正方法，应用局部应力应变Neuber 近似法对舵板的疲劳寿命进行了预计。

1 局部应力应变Neuber 方法

近代在应变分析和低周疲劳的基础上，采用一种新的疲劳寿命估算方法——局部应力应变法。它的设计思路是:零构件的疲劳破坏都是从应变集中部位的最大应变处起始，并且在裂纹萌生以前都要产生一定的塑性变形，局部塑性变形是疲劳裂纹萌生和扩展的先决条件。因此，决定零构件疲劳强度和寿命的是应变集中处的最大局部应力和应变。其基本假设是:若同种材料制成构件的危险部位的最大应力应变历程与一个光滑试件的应力应变历程相同，则它们的疲劳寿命就相同。

因此有应力集中零部件的疲劳寿命，可以使用局部应力应变相同的光滑试件的应变－寿命曲线进行计算，也可使用局部应力应变相同的光滑试件进行疲劳试验来模拟。

用局部应力应变法估算谱载荷下的疲劳寿命［1］，可以使用载荷－应变标定曲线法、修正Neuber法和能量密度法等，本文采用常用的修正Neuber法，它是一个近似的经验方法。

图1 Neuber 近似法Fig.1 Neuber rule

该方法需要的原始数据包括:名义应力谱Si-n，疲劳缺口系数Kf(联系光滑试件与缺口试件疲劳强度的静态参数，与很多因素有关，目前尚无精确计算方法)，弹性模量E，循环应力－应变曲线Δσi=fi(Δεi)。其求解步骤如下:

2)由可用性系数F和循环应力应变曲线求出响应的双倍Δσ - Δε 曲线;

3)求交点Pi(Δσi，Δεi);

4)修改可用性系数;

5)得此应力应变在绝对坐标系(σ，ε)中的值σi和εi，并返回1)。

2 材料力学性能试验分析

2.1 循环应力应变试验

舵板材料为18Cr2Ni4WA，实验按照GB/T228.1－2010《金属材料拉伸试验 第1 部分:室温试验方法》进行拉伸加载及卸载。试验采用美国MTS Landmark 电液伺服试验系统，最大拉伸力500 kN。应变测试系统为DH3821 准静态应变测试采集系统。拉伸试验试件尺寸及照片，如图2所示。

图2 循环应力应变试件尺寸及照片Fig.2 Dimensions and pictures of cyclic stress-strain test specimens

通过试验数据可得到材料的弹性模量E 、屈服强度σs、抗拉强度σb和真实断裂强度σf等参数。试验件界面收缩情况如图3所示。断面收缩率Ψ 由试件断口面积及初始面积计算得到，真实断裂延性εf则根据断面收缩率计算得到，结果如表1所示。

表1 18Cr2Ni4WA的拉伸工况材料参数Tab.1 Materila's parametric based on tension test of 18Cr2Ni4WA

图3 拉伸试件界面收缩情况Fig.3 Shrink of the tension test specimen's interface

假设应变幅值与应力幅值关系曲线符合方程:

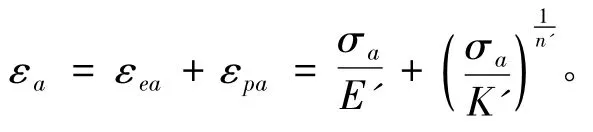
可拟合出3个待定系数循环弹性模量E′ 、循环强化系数K′和循环应变硬化指数n′ 分别为:110.29 GPa，1.2073 GPa和0.0409。

2.2 应变－寿命曲线

通常采用Δε - N 曲线描述材料的应变和寿命之间的关系。在所有Δε - N 曲线中，Manson-coffin 经验公式应用最广，其表达式包括弹性应变和塑性应变两部分:

式中:σ′f为疲劳强度系数;ε′f为疲劳延续系数;b为疲劳强度指数;c为疲劳延续指数。

本文没有直接采用疲劳实验获取应变－寿命曲线，而是前述材料的静态拉伸实验近似估算材料的疲劳性能数据。通用斜率法、四点关联法及改进的四点关联法等3 种方法估算材料的应变－寿命曲线，见表2和表3。

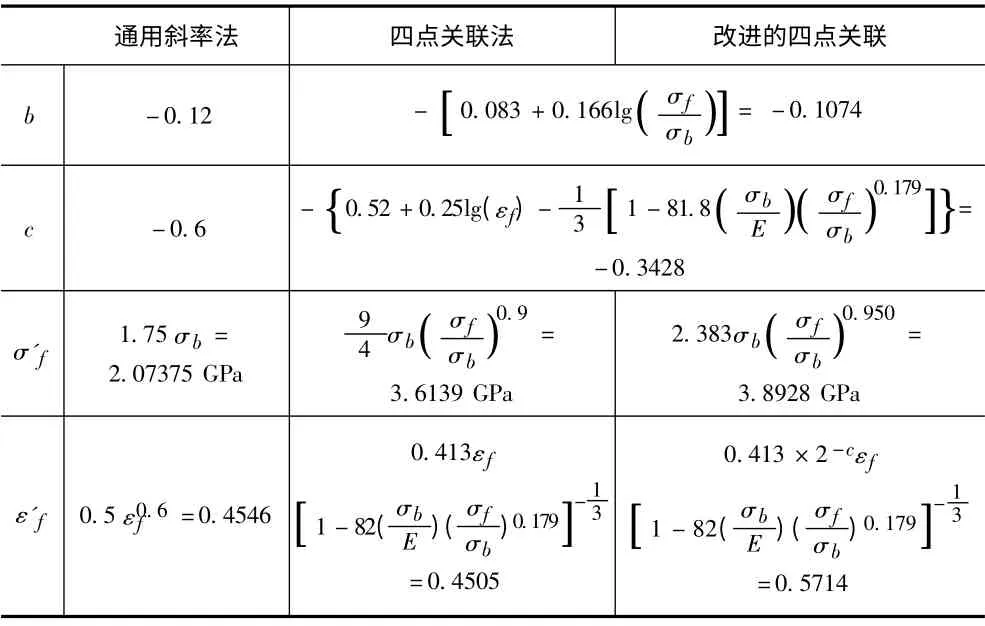
表2 Manson-coffin 公式中疲劳常数估算方法Tab.2 Fatigue parametric' estimation methods of Manson-coffin formula

根据表2 中的方程待定系数，分别给出18Cr2Ni4WA 材料的3 种评估方法的公式，如表3所示。并据此绘制出应变－寿命曲线，如图4所示。

表3 三种估算公式(Δε - N)Tab.3 Three estimation formulas of Δε - N

图4 18Cr2Ni4WA 应变－寿命曲线Fig.4 Δε - N curves of 18Cr2Ni4WA

由图4 可知，通用斜率法得到的S-N 曲线安全系数最大。

上述应变－寿命曲线以Re= - 1 时的应变幅为参数描述材料的寿命特性，当Re≠- 1 时需要对曲线进行修正。本文的Re= 0 ，为非对称应变循环，相应的Manson-Coffin 公式有多种修正方法。

1)Morrow 弹性应力线性方法

用Morrow 弹性应变线形方法对Manson-Coffin 公式修正为:

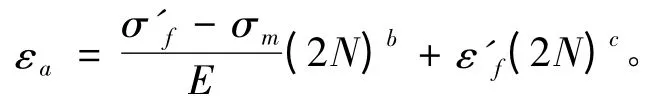
相应的应力－寿命曲线估算公式，如表4所示。

表4 用Morrow 弹性应力线性方法修正后的Δε - N 估算公式Tab.4 Δε - N revised estimation formulas by Morrow linear elastic stress method

2)Gerber 弹性应力曲率方法

用Gerber 弹性应力曲率方法对3 种Manson-Coffin 公式修正为:

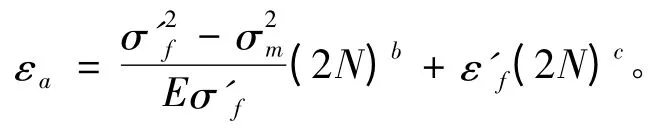
相应的应力－寿命曲线估算公式，如表5所示。

表5 用Gerber 弹性应力曲率方法修正后的Δε - N 估算公式Tab.5 Δε - N revised estimation formulas by Gerber linear elastic stress method

3)Morrow 总应变法

用Morrow 总应变法对3 种Manson-Coffin 公式修正为:

相应的应力－寿命曲线估算公式，如表6所示。

表6 用Morrow 总应变法修正后的Δε - N 估算公式Tab.6 Δε - N revised estimation formulas by Morrow strain method

4)Sachs 弹性法

用Sachs 弹性法对3 种Manson-Coffin 公式修正为:

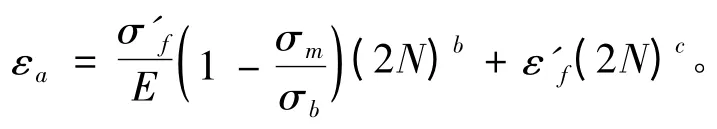
相应的应力－寿命曲线估算公式，如表7所示。

表7 用Sachs 弹性法修正后的Δε - N 估算公式Tab.7 Δε - N revised estimation formulas by Sachs linear elastic stress method

将表4～表7 中应用4 种修正方法对3 种寿命估算方法的结果绘制成曲线，如图5所示。

图5 四种修正结果对比Fig.5 The Δε - N curves by four revised methods

由图5 知，使用Morrow 总应变修正方法得到的S－N 曲线安全系数最大。

3 危险点的应力应变载荷曲线

舵板在训练模拟系统弹体上的位置，如图6所示。根据舵板冲击仿真分析研究的仿真结果，提取与实测速度最为接近工况下的危险测点应力时间历程，作为寿命评估的载荷谱［5］。

从仿真分析结果中直接提取舵板上对应图7的多个危险点Von Mises 等效应力的时间历程响应，结果如图8所示。该方案中只考虑一个舵板、忽略了舵板在弹体上的不同排列顺序、且有限元网格左右对称，No.1和No.2的应力响应完全一致。No.3选在舵板上和弹体耳座上时，应力差别较大，说明该处的应力梯度大。

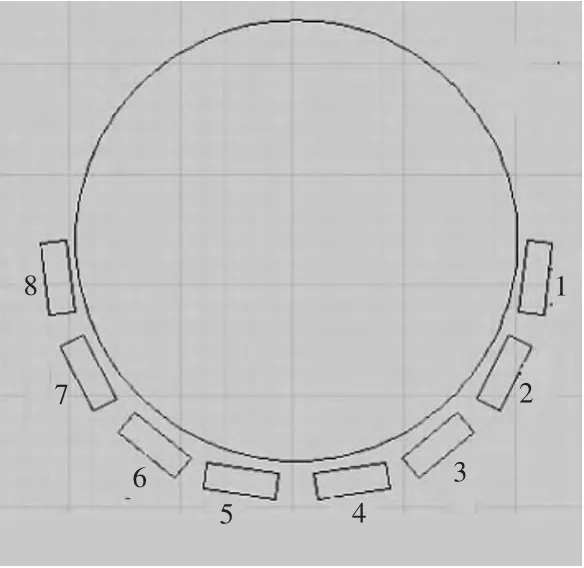
图6 舵板编号及其在弹体上的位置Fig.6 The helm's serial number and it's location on the missile bodies

图7 测点(No.1～No.3)的位置Fig.7 Gauging points' location (No.1～No.3)

4 舵板结构冲击疲劳寿命预测

根据危险点等效应力－时间历程曲线，应用雨流计数法和疲劳累积损伤理论进行寿命预测方法如下:每一循环过程所引起的损伤计算均基于应变－寿命关系曲线。由于目前尚不存在适用于各种工况的最佳损伤计算公式，本文选用2 种常用的损伤计算方法分别计算，并进行比较，从中选择较安全的结果。

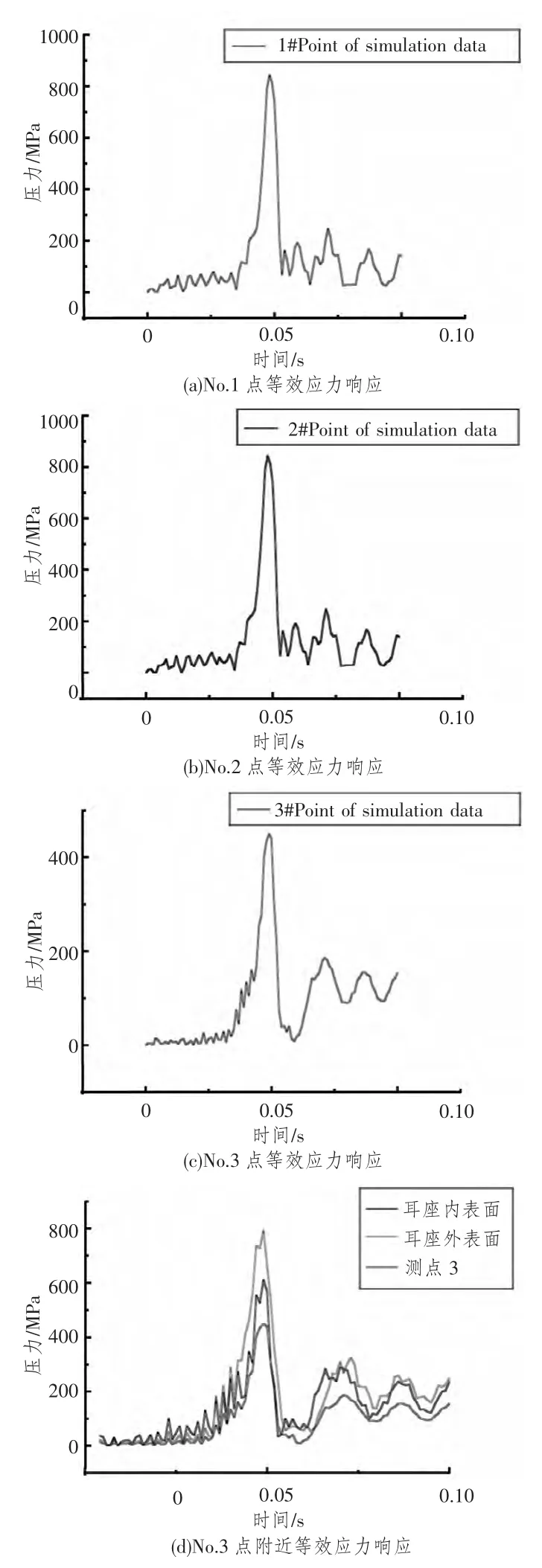
图8 舵板危险点的应力－时间历程Fig.8 Stress time history of hem' dangerous point

1)道林(Dowling)损伤计算公式

当εp＞εe时，按塑性应变分量计算:

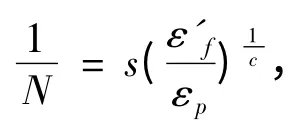
当εp＞εe时，按弹性应变分量计算:

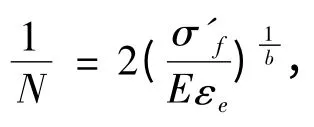
若考虑平均应力，则

2)兰德格拉夫(Landgraf)公式

考虑平均应力的影响进行修正后，相应的损伤公式为:

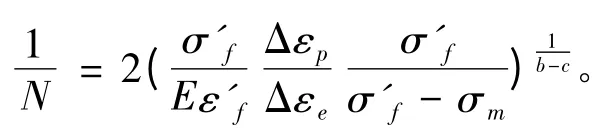
应用上述公式确定疲劳损伤后，根据疲劳累积损伤理论可计算出寿命。目前已提出几十个疲劳累积损伤理论，其中应用较多的是迈因纳(Miner)线性累积理论。该理论假定:1)相同应变幅值和平均应力的各次循环造成的损伤可线性叠加;2)损伤累积到1 时，疲劳破坏发生，即

该法则忽略了加载次序和剩余应力非线性的影响，对有些问题精度较低，但实施简单，只需等幅冲击实验即可。应用2 种损伤预测公式预测结果见表9。

表9 疲劳寿命预测结果(通用斜率法)Tab.9 Fatigue-life's estimation results (universally gradient method)

表9 中2 种损伤公式计算结果均显示:冲击疲劳寿命主要取决于峰值较大的少数几次应力时间历程造成的损伤，如D1和D2;因此舵板冲击峰值的大小直接影响寿命预测的准确性，其中兰德格拉夫损伤公式预测的寿命偏安全，为12 次。

5 结 语

本文主要针对舵板材料18Cr2Ni4WA和舵板冲击仿真分析研究中舵板关键部位的等效应力－时间历程曲线，通过材料实验获取相关数据后，应用局部应力－应变法对舵板结构冲击疲劳寿命进行了预测，得出结论:

1)对低周大能量冲击疲劳工况，取件位置对拉伸和冲击实验结果几乎没有影响。

2)该材料表现出轻微的循环软化现象，即:随着冲击次数的增加，在相同冲击载荷作用下，产生的总应变会越来越大，每次冲击带来的损伤不均等。直接应用传统的线性累积损伤理论会带来误差，需要适当修正。

3)在仿真结果提供的载荷谱作用下，按安全系数为3 计算，应用通用斜率法和兰德格拉夫损伤计算公式得到的冲击次数为12 次。

［1］姚卫星.结构疲劳寿命分析［M］.北京:国防工业出版社，2003.

［2］舒陶，任宏光，郭克平.局部应力应变Neuber法与有限元求法的比较［J］.弹箭与制导学报，2009，29(1):267－269.SHU Tao，REN Hong-guang，GUO Ke-ping.Comparison of neuber's rule and FEM for local stress-strain［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2009，29(1):267－269.

［3］邹远鹏，胡光立.小能量冲击疲劳研究的新进展［J］.机械强度，1991，13(1):52－56.

［4］赵少汴.局部应力应变法及其设计数据［J］.机械设计，2000，17(2):1－4.ZHAO Shao-bian.Partial stress-strain approach and its design data［J］.Journal of Machine Design，2000，17(2):1－4.

［5］孙凌玉.基于流固耦合的舵板冲击仿真计算［R］.中船重工第七一三研究所，2007.