有限元模型修正中处理不完备实测模态参数的方法研究

张 淼，徐慕奇，许鑫鑫，陈钱钱

（1.长春工程学院理学院；2.长春工程学院国际教育学院，长春130012）

0 引言

有限元模态修正时，在准备好有限元计算的解析模态参数与实验模态参数这2种数据后，接下来就要进行模型的匹配了，这是因为实测的模态参数多数情况下都是不完备的。一般来说，试验的测量网点与有限元模型的节点并不能完全对应。首先，实验时的某个测量点未必能与有限元模型的某一节点对应，但只要解析模型的建立者与试验方案的设计者之间进行足够的沟通即可避免这个问题。其次，有限元模型通常含有比实测的自由度多得多的自由度，而对于大多数的有限元模型修正的常用技术来说，都要求确保解析模型和实验模型的自由度必须完全匹配。为了解决这种网点的不一致性，要么必须减少解析模型的系统矩阵维数，使之与实验设置的自由度数相等，要么必须将实验数据扩展至有限元解析模型所需要的自由度数，这就需要进行不完备实测模态参数的处理。本文在综述过程中所使用的符号依据如下2个原则，第1个是在对多个参考文献的内容进行综述时尽量使各参考文献中所使用的符号在本文中能够得到一定程度上的统一，在不产生歧义的情况下以便于读者阅读；第2个是没有完全使用独立于参考文献中的符号，否则将不便于读者查阅原文。

1 实模态参数与复模态参数理论［1－2］

描述自由度为N的线性阻尼离散系统的自由振动方程为

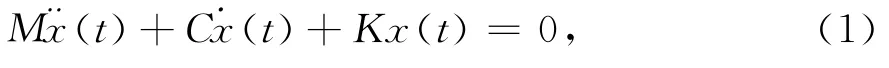
式中M、C和K ∈RN×N分别为质量、阻尼和刚度矩阵。

从有限元模型修正出发，由拉氏域的运动方程

经过特征分析而得到的方程

令λi＝－，则式（3）可化为

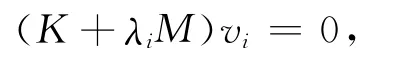
可以计算得到实频率（无阻尼固有频率）及实模态（振型）。记V ＝ ［v1，…，vN］为无阻尼规范化振型矩阵，那么此时模态质量和模态刚度矩阵分别为

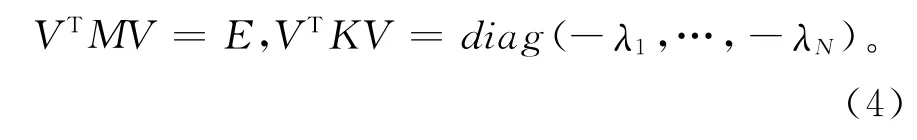
对经典阻尼系统有

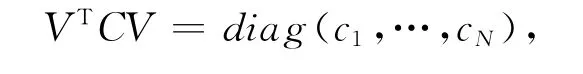
考虑含有阻尼时的系统极点及复模态对（si，ui）（i＝1，2，…，2 N）满足方程

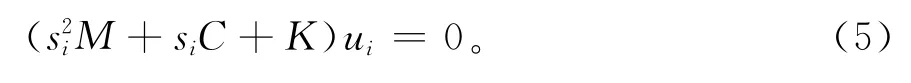
对于N自由度振动系统，特征方程det［s2M＋sC＋K］＝0有2 N个呈复共轭对出现的特征值s1，s2，…，s2N（其中si＋1为si的共轭（i＝1，3，…，2 N －1）），称为系统的复频率。这些复频率对应着一组呈复共轭对出现的特征向量ui∈CN称为系统（1）与si相对应的第i个模态向量。将u1，u2，…，u2N（其中ui＋1为ui的共轭（i＝1，3，…，2 N－1））称为复模态，复频率和复模态统称为复模态参数。它们的正交条件的形式有很多，常用的形式为

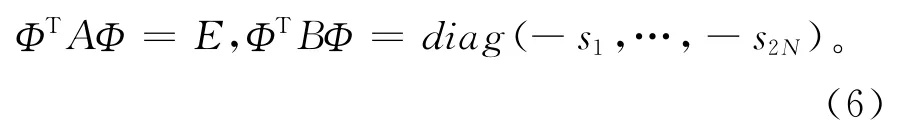
其中状态向量矩阵为Φ ＝ ［φ1，φ2，…，φ2N］，状态向量为φi＝ ［uisiui］T（i＝1，2，…，2 N），且

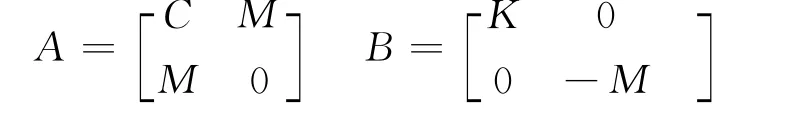
下文讨论中用到的均为规范正交化后的实模态vi（i＝1，2，…，N）和复模态ui（i＝1，2，…，2 N）（见式（2）和式（6））。

2 模态参数的识别与估计

系统按阻尼比的大小可分成过阻尼系统（ξ＞1），临界阻尼（ξ＝1）和欠阻尼（ξ＜1）系统，过阻尼系统的响应只有衰减成分，而没有振荡趋势，而欠阻尼系统的响应是一种衰减振荡，临界阻尼是过阻尼与欠阻尼的一种分界。实际系统的阻尼比很少有大于10%的，除非这些系统设置有很强的阻尼机制，因此多数情况下，我们只研究欠阻尼系统的情形。实测主要针对无阻尼固有频率及振型，而测量阻尼比的目的之一是当阻尼比很小时，实测频率才与无阻尼固有频率一致。

根据实验目的的不同，我们可以选择不同的参数估计方法，估计复模态或纯模态。如果要进行模型修正，那么实验模态就应当是实模态。一般来说，一个系统的动态响应是它的若干阶模态振型的迭加，但如果假定在给定的频带内只有一个模态是重要的，那么该模态参数可以单独确定。以这一假定为根据的就是所谓的模态参数识别方法。就系统矩阵而言，模态振型向量服从正交性条件，这些正交性条件又决定了模态比例因子。时域方法——直接以输入和输出信号时间历程估计参数；频域方法——以输入和输出信号在频域中的关系为依据估计参数。均匀离散的信号经由傅丽叶变换可以很容易地在时域和频域之间变来变去。

如果模态分析实验的目的是为了得到实模态，那么分析者应该选择能够估计这类模态的方法，例如最小二乘频域方法（近似方法）和频域直接参数识别方法（精确方法）。比例阻尼时，特征值与无阻尼时的特征值稍有不同，特征向量与无阻尼时的特征向量完全相同［3］。比例阻尼或无阻尼系统的极点都是复值的，而且为纯虚的，它们的模态为实模态，然而非比例阻尼系统具有复值极点和复值模态振型。一般对于欠阻尼结构，假定它是比例阻尼还是非比例阻尼差别并不大。对于阻尼较大的结构，特别是那些具有集总阻尼部件的结构（例如装备完善的汽车），多半认为是非比例阻尼的。如需实模态分析（K＋λ2M）v＝0，则实测出ωr，vr，其中λr＝iωr，如需复模态分析（s2M＋sC＋K）u＝0，实测出sr＝δr＋iνr，ur也能测得。如果无阻尼或阻尼比很小时，ωr＝νr。

3 模型缩聚

解决测量自由度远小于有限元模型解析自由度这一矛盾的一个途径是模型减缩，即将模型的位移基缩聚到测量自由度上。事实上，要鉴别与每一个实验自由度相对应的解析自由度，这一操作的具体过程就是定义一组“有效”自由度，而其他的解析自由度叫做“废弃”自由度。仅仅得到解析自由度与实验自由度的相应关系后，实验模态与解析模态及系统矩阵的维数仍然是不相同的，因此要通过缩减方法来解决尺寸不一致的问题。

缩减技术是通过一个变换矩阵TD或TF定义有效自由度与废弃自由度之间的一种关系：

式中：XA是有效自由度；XD是废弃自由度；XF是全部自由度；TF用于压缩系统的质量和刚度矩阵。

有很多的减缩方法可供使用，其中经典的方法之一是静力缩聚，或 Guyan－Irons减缩［4］。我们选测量自由度为主坐标（有效自由度）xm，其余的自由度为副坐标（废弃自由度）xs，于是位移基（全部自由度）缩聚到主坐标上

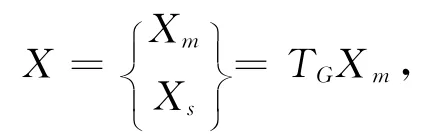
将M与K也同理进行分块，分块后的运动方程（2）可写成

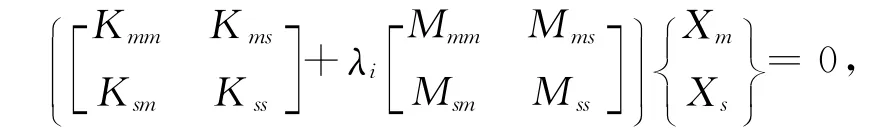
式中Guyan减缩矩阵为

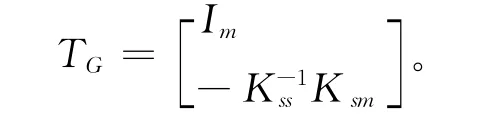
式中Im是m×m的单位矩阵，常把Csm＝－称为原始模型的约束模态。Guyan减缩有多种改进，比如O'Callahan的改进是引入惯性项作为准静态力［5］，它的缩聚矩阵是

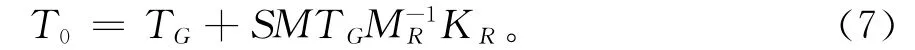
其中

式中MR，KR是压缩质量矩阵和压缩刚度矩阵。

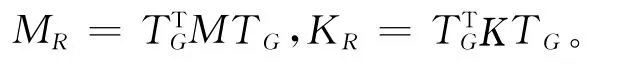
还有一种方法是利用原模型计算特征向量［6］，再去生成主、副坐标之间的变换，以φ表示有限元模型计算的前r阶解析特征向量，按主、副坐标的分块形式是

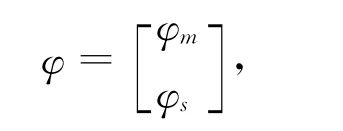
利用模态缩聚变换，得到

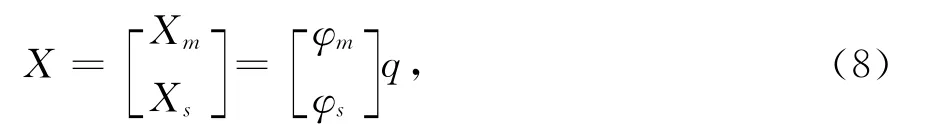
由第一分块式得

式中的广义逆矩阵（当主坐标个数大于实测模态个数时）为

把方程（9）代入式（8），可得到压缩阵为

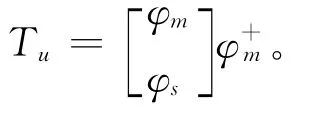
至今已有很多模型缩聚方法，除上述提到的几种之外，比较成熟的有矩量匹配法、代价分析法（Cost Analysis）、最优投影法（Optimal Projection）、平衡降阶法（Balanced Reduction）以及这些方法的组合。在大规模动力系统的降阶建模中，克雷洛夫子空间技术（Krylov Subspace Tecnique）得到人们的极大关注，它已经在各种动力系统，包括二阶和非线性系统中获得了广泛的应用并取得了巨大进展。

另一种得到广泛应用的是Kidder模型缩聚法［7］，它能保留式（7）中的惯性量，并能获得较高精度的模型修正结果。这里简要介绍运用Kidder原理缩减解析模型的刚度和质量矩阵，使得它们与实测的振型分量φm的维数保持一致，设得到结构动力模型的所有节点上的振型分量为

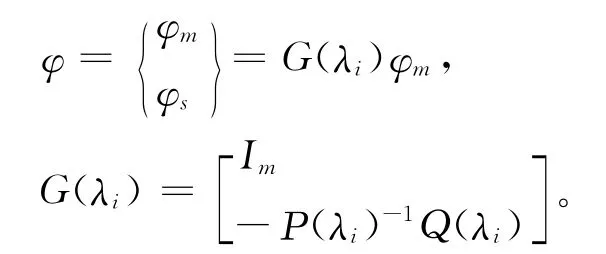
式中Im是m×m维的单位矩阵，逆矩阵P（λi）－1和矩阵Q（λi）通过式（10）～ （11）得到

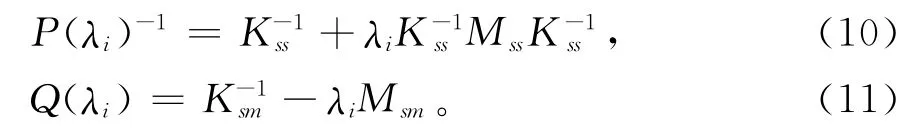
因此，缩减后的刚度和质量矩阵分别为

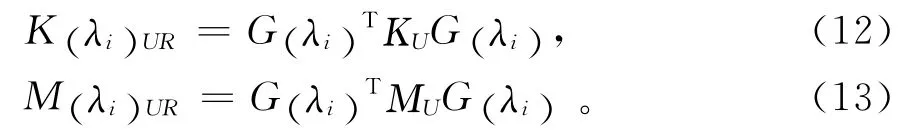
式（12）～（13）中的刚度和质量矩阵必须满足如下的正则方程

式中：Λ是t×t维的由实测频率构成的对角阵；φm是对应的m×t维的实测振型矩阵；t为测量数据的个数。

有限元解析模型的缩减过程就是把废弃自由度从解析模态振型及系统矩阵中剔除。模态振型的压缩思想极为直截了当，从模态振型中把废弃自由度抹掉就可以了，但针对系统矩阵的缩减就不那么简单了，必须采用上述的缩减技术。在实际中各种缩减技术的正确性都会受到一定的限制。压缩后的系统矩阵只是在一个或若干个特定的频率上能准确描述有效自由度的动态特性。除此之外，系统矩阵一旦经过压缩，它的连通性就会受到破坏。然而由于压缩技术针对的是比较整体的测量数据，并且这种压缩结果在特定的频率上具有明确的物理意义，因此使用压缩解析系统矩阵方法常常比使用扩展实验模态振型方法在处理不完备实测模态参数时要更具有优越性［8］。

4 模型扩展

有限元解析模型的自由度数一般总是大大超过实验测量的自由度数，有限元建模分析要求细密的节点网格作为支撑，但是在实际结构上测出所有对应的自由度是不现实的，甚至是不可能的，这是因为：首先许多有限元节点处于结构的内部，无法进行测量，其次转动自由度确实难以测量，最后对于实验模态分析来说，细密的测量网格是不必要的，常常也是不实际的。然而大多数的模型修正方法都要求解析自由度与实验自由度之间具有一一对应关系。对这样的2组数据，自由度的数目及位置必须相同。

对于大型结构来说，要想在所有自由度上测全数据是很难的。但在进行结构动态设计时，由于给出的目标振型是理想振型，不存在误差平滑问题，故可采用振型自由度的直接扩展方法。扩展技术是把测量得到的模态振型扩充到有限元解析模型的全套自由度上。大多数扩充技术都采用的是把有限元模型的计算振型数据用来扩展实测模态振型的数据。但应用时一定要注意不要偏离实测模态振型数据所给出的信息。

实测模态振型中的未知废弃自由度的估算常常是以解析模型中有效自由度与废弃自由度之间的关系为依据进行的。因此各种压缩技术都可以被用作扩展技术，因为压缩技术定义的是解析模型的有效自由度与废弃自由度之间的一种关系：

同样的变换矩阵可用于实验模态振型

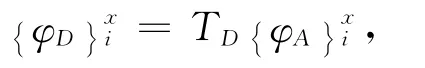
注脚x表示实测数据。

下面针对实模态参数介绍一种扩展技术［9］。假定系统有限元模型第i阶振型为φi，当实测自由度小于解析模型自由度时，将振型分块为

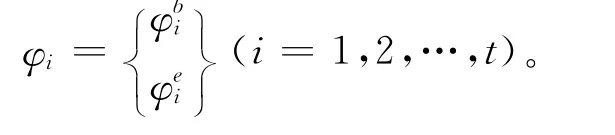
于是，将M与K也同理进行分块，分块后方程（2）可写成：

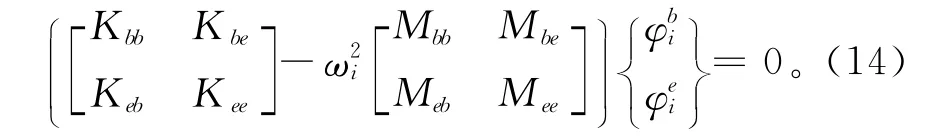
式中：ωi为第i阶实测固有频率为第i阶不完备的实测振型。

将式（14）展开，由第2行得

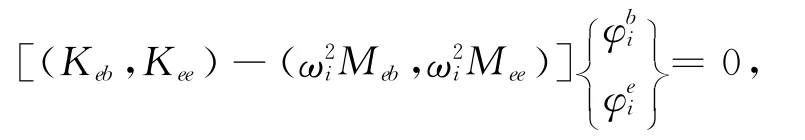
即

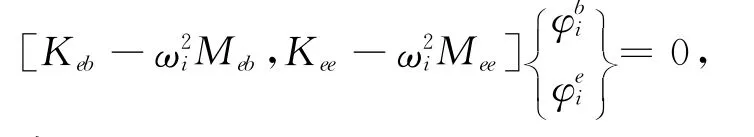
那么有

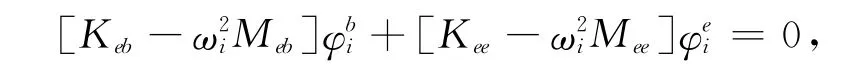
可得：

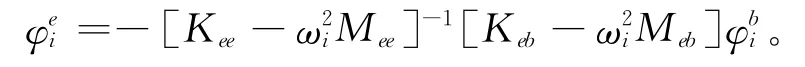
因此，

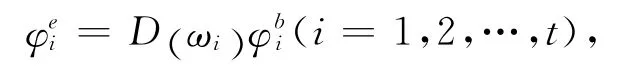
其中：

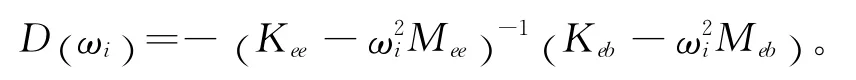
令

则有实测振型的扩展式：

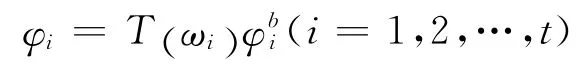
现有的修正方法，特别是参数型修正方法，一般都只考虑实模态的情况，但在实际结构中，复模态情况更为普通，虽然Ibrahim曾提出过从复模态中提取实模态参数的方法［10］，但由于其结果的唯一性没有解决而不便实用。

近年来文献［11］提出了一种利用不完备复模态参数修正结构有限元模型的迭代修正方法，认为结构有限元模型误差主要来源于某些形状或物理性质太复杂的局部，其结构质量与刚度矩阵的误差可直接由这些局部的几何、材料参数来修正，质量、刚度矩阵的误差同时又影响阻尼矩阵，将阻尼阵表达为质量、刚度矩阵的多项式，再通过修正多项式系数来修正阻尼矩阵。文中还讨论了复模态振型的扩充问题。当测试自由度小于解析模型的自由度时，将第i阶复振型Ψi按已测量与未测量自由度进行分块：

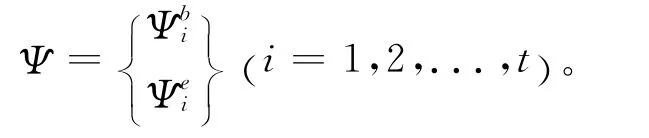
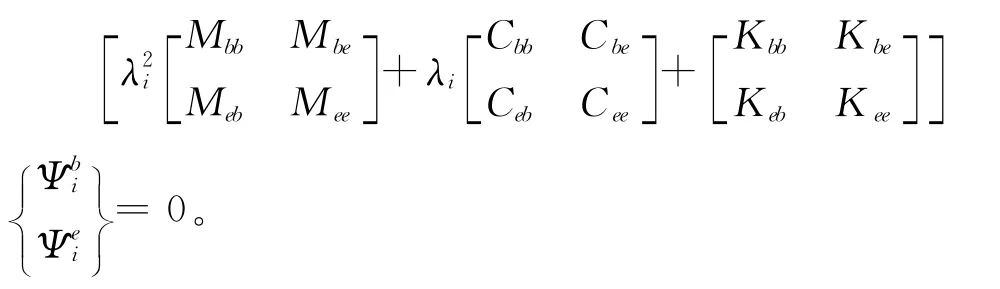
由上式第2行可得：

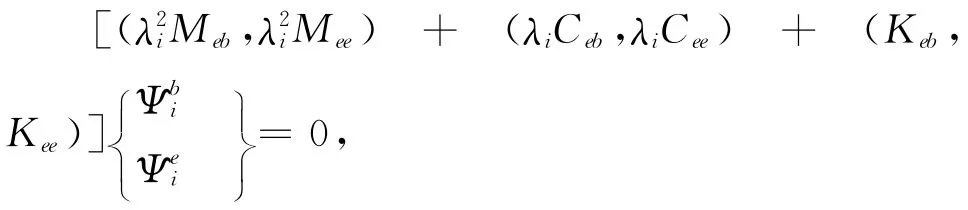
即

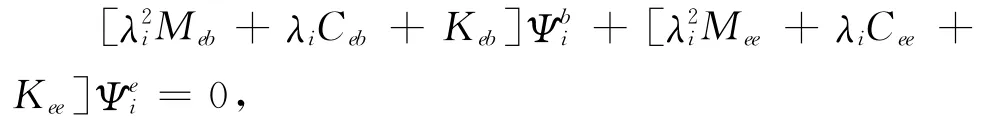
那么

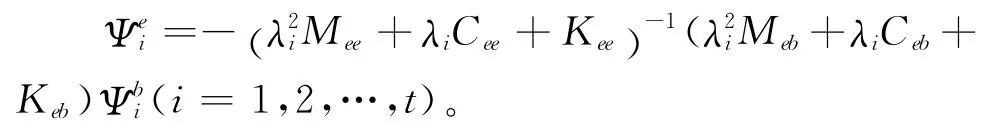
简记上式为：

则有实测振型的扩展式

利用式（15），可对第i阶复振型进行扩展，即通过已测量自由度上的复振型计算未测量自由度上的复振型。

再讨论另外几种扩展技术：

特征向量混合法是把相应的解析模态振型的值填补到实验模态振型中所缺失的自由度上

填补之前，解析模态振型和实验模态振型必须加以比例换算，使二者长度相等：

注脚a表示解析数据。

模态坐标法是把实测模态振型定义为解析模态振型的线性组合，该线性组合的系数根据有效自由度来计算：

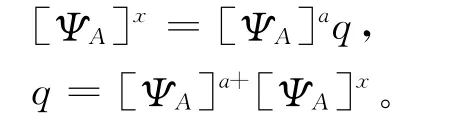
然后利用矩阵q来估计实测振型中所缺失的自由度：

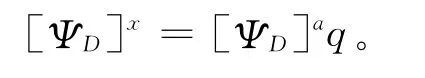
对于有效自由度来说，原来的测量值可以保留，也可以用它们在解析模态振型组合上的投影代替，这样做对实验模态振型来说具有平滑的效果。

插值法也可以用来估计缺失的自由度，插值法的一个优点是，扩展实验模态振型时不必用解析数据，该方法在很大程度上依靠的是不同自由度之间的连通性，因此每个插值绝不可能独立，这就使它的实际应用变得相当困难。实践中，插值法的应用只限于一维部件所组成的结构。当有效自由度组仅由直线自由度组成时，用插值法对转动自由度的估计也是一种数值上不稳定的过程。

近年来文献［12］利用动态扩充法进行模态扩展进而进行模型修正时，提出了一种新的迭代方法，在模型修正过程中考虑了误差项，并将其以修正项的形式添加到模型修正当中，同时该方法没有限定所使用模型修正的方法，具有一定的通用性。如果将模型缩聚直接应用到模型修正中，模型缩聚的近似带来的误差会影响到模型修正的精度。因此文献［13］提出将模型缩聚和模型修正之间关系进行整合，将模型缩聚技术与模型修正过程有效结合，提高了模型修正的精度。主要方法是在用修正元的线性组合式和为拟修正系数）表示出有限元模型的刚度、质量阵与物理模型的刚度、质量阵之间的关系ΔK＝Ka－Kt和ΔM＝Ma－Mt后，事实上得到了模型修正方程，然后提出了物理模型和有限元模型的缩聚矩阵的概念，认为多数修正方法都令这2个缩聚矩阵是相等的，但当有限元模型与物理模型差别较大时，该恒等假设所带来的误差会较大，进而影响修正的精度，因此文献提出在修正过程中打破这种恒等假设，形成新的修正系数的迭代方程。

5 位置矩阵法［14］

当结构比较复杂时，只能测量得到部分信息，在这种不完备信息的情况下，修正矩阵中的修正元ΔM，ΔC，ΔK没有唯一解，这里将质量、阻尼和刚度矩阵的修正量局部化，利用位置矩阵将修正量集中在测量自由度上，则有

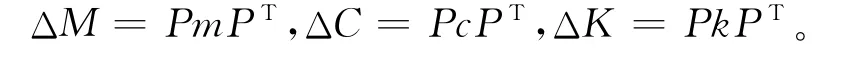
式中：m，c，k均为r×r阶的实对称矩阵；r为测量自由度数目；P∈Rn×r称为位置矩阵，它是由n阶单位阵划去非测量自由度对应列所构成的矩阵。

6 利用实测复模态计算解析实模态［10，15］

在实际结构中，阻尼矩阵一般为非比例阻尼，且实测模态的数目小于结构自由度，即实际情况中多为不完备复模态条件，对于线性结构来说，识别后得到复模态满足

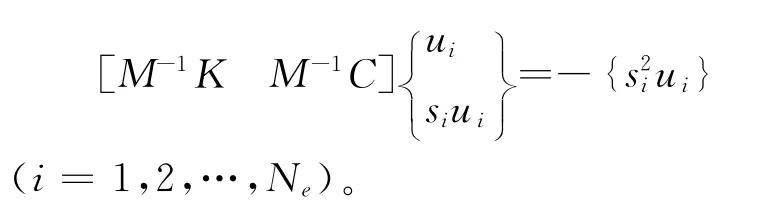
（si，ui）（i＝1，2，…，Ne）为实测复模态参数，由于实测自由度数目Ne与有限元结构自由度数目N不符，因此上述方程不能解出M－1K，为此补充解析高阶复模态所满足的那部分方程

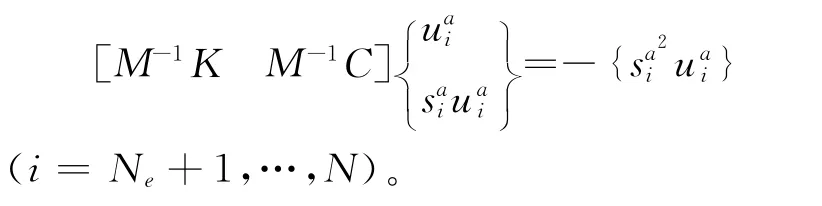
用最小二乘法解出M－1K，再用解析方法

7 结语

本文通过把有限元模型修正中处理不完备实测模态参数有关的基本知识、常用方法及最新进展进行综述，展示了这一应用领域中所包含的技术基础、内在联系和应用特点，为相应的有限元模型修正的前期数据处理提供了良好的技术支持。

［1］张淼，陈庆文.两种常见的状态方程及其特征向量的正交性［J］.长春工程学院学报（自然科学版），2011，12（2）：122－125.

［2］张淼，周福全，王震.工程中广义特征问题的讨论［J］.长春工程学院学报（自然科学版），2013，14（4）：5－10.

［3］张淼，于澜，鞠伟.复模态正交性理论的异常现象及对策分析［J］.应用数学和力学，2014，35（10）：1081－1091.

［4］Friswell M I，Penny J E T，Garvey S D.Using linear model reduction to investigate the dynamics of structures with local non－linearity［J］.Mechanical System and Signal Processing，1995，9（3）：317－328.

［5］朱宏平，徐斌，黄玉盈.结构动力模型修正方法的比较研究与评估［J］.力学进展，2002，32（4）：513－525.

［6］宋汉文，王丽炜，王文亮.有限元模型修正中若干重要问题［J］.振动与冲击，2003，22（4）：68－71.

［7］Kidder R L.Reduction of stiffness and mass matrices［J］.AIAA Journal，1997，3（11）：892－898.

［8］Ward H，Stefan L，Paul S.Modal Analysis Theory and Testing［M］.Brussel，Belgium：Katholieke Universiteit Levven，1997.

［9］徐静，董雁，李静敏，等.有限元模型修正法在结构动态设计中的应用［J］.浙江海洋学院学报（自然科学版），2001，20（2）：139－142.

［10］Ibrahim S R.Computation of normal modes from identified complex modes［J］.AIAA Journal，1983，21（3）：446－451.

［11］冯文贤，陈新.基于实验复模态参数的有限元模型修正［J］.航空学报，1999，20（1）：11－15.

［12］李伟明，洪嘉振，张以帅.新的模型修正与模态扩展迭代方法［J］.振动与冲击，2010，29（6）：4－7.

［13］张以帅，洪嘉振，李伟明.模型缩聚——模型修正迭代方法的研究［J］.振动与冲击，2009，28（12）：23－26.

［14］朱凼凼，冯咬齐，宋海丰.一种基于加速度频响函数的动力学模型修正方法［J］.固体力学学报，2005，26（3）：329－332.

［15］祁泉泉，辛克贵.基于不完备复模态的有限元结构模型修正［J］.清华大学学报（自然科学版），2011，51（6）：750－754.