软土深基坑变形性状的时间效应研究

王继东，储勇，肖建勋

（1.无锡市水利设计研究院有限公司，江苏 无锡 214000；2.南京军区合肥房地产管理处，安徽 合肥 230001；3.江苏省地质工程有限公司，江苏 南京 210018）

0 前 言

开挖问题与岩土工程中其它问题的主要区别在于，土方开挖使坑底土体应力处于释放状态，由于卸荷而在坑底土体中产生超静负孔压。另外，挖方通常是分层、分阶段进行的，施工过程和边界条件的改变使问题的研究更加复杂。

在软粘土地基中进行的深开挖工程具有时间效应。开挖期间基坑性状的改变是由开挖卸荷所致，而开挖间歇期内的变化一般是由于土体的固结和蠕变所引起的。本文所要研究的是土体的固结及蠕变对基坑开挖的影响。

1 软土的固结理论

1.1 比奥(Biot)固结理论

无论是单向还是准三维固结理论，都只研究了土体中超静孔压的消散过程，而并没有涉及到与位移场的耦合作用。为了能将土骨架变形和孔隙水渗透(或孔压消散)同时考虑，1941年，Biot推导了真正意义上的真三维固结方程：

方程式（1）和（2）即为Biot三维静力固结方程，也是有效应力(静力)分析法的控制方程。

1.2 Biot三维固结有限元基本方程

Biot三维固结有限元方程的推导可分为两步：先对Biot三维固结方程进行空间离散，然后再进行时间离散：

1.3 Biot三维固结问题的有限元法求解过程

前文已得到Biot三维固结有限元基本方程和计算公式，现进一步对用有限元法求解三维固结问题的整个过程作一简单描述：

①空间和时间离散；

②固结有限元方程的整体组装；

③引入边界条件；

④求解线性方程组；

⑤计算当前节点位移和孔压；

⑥计算节点应力；

⑦时段循环。

1.4 比奥(Biot)固结理论的推广

Biot固结理论是针对线弹性土体建立起来的，但也可以推广应用于建立在非线性基础上的粘弹塑性。Biot固结理论中力的平衡方程、体积变化连续性方程，均与土的应力-应变关系无直接联系，故无需作任何变动即可解决饱和流变土体的固结问题。

2 工程实例

南京佳兆业城市广场基坑长269m、宽19.64m，采用地下连续墙，墙厚600mm，深25m，加钢管内支撑(Ф609)，标准段处的支撑和标高如图1所示。具体施工过程为：首次开挖两道撑的深度，开挖标高为-5.6m，无支撑暴露时间控制在16h，开挖时间为10d；第二次开挖到第三道支撑标高处，无支撑暴露时间控制在12h，开挖时间为15d；第三次开挖到第四道支撑处，无支撑暴露时间控制在8h，开挖时间为12d；第四次开挖至坑底标高，且在2d内开始浇筑垫层及底板，开挖时间为6d。

2.1 有限元模型的建立

2.1.1 计算区域的确定

基坑开挖高度均为12.3m，降水影响范围以库萨金公式求得的最大降水影响半径和工程经验值为参考，并在实际建模中作调整。本文取降水影响半径为100m。所以，取计算范围长为200m，计算深度为85m。

2.1.2 土的模型、单元划分及边界条件

土的本构模型采用考虑蠕变的扩展Drucker-Prager蠕变模型进行计算。其中：β 为材料的内摩擦角；d 为材料的内聚力；A、n、m为材料的蠕变特性参数。在地下连续墙与土体之间设置接触面，接触面无厚度，小滑移。接触面的本构关系为：切线方向采用Mohr-Coulomb摩擦模型，μ=0.2，法线方向为刚性，即不允许接触面的相互嵌入。考虑人工填土以下土层中孔隙水影响。土体采用减缩积分的四节点平面应变孔压实体单元CPE4RP，共划分了7727个单元。地下连续墙采用四节点平面应变单元CPE4R，支撑采用杆单元T2D2，地下连续墙共划分了100个单元，边界条件为：计算域左右两侧水平方向位移约束，为定水头边界，底面水平和竖直方向均约束，底面边界为不透水边界，每步开挖结束后基坑底面孔压为零。

2.2 计算结果及分析

土体的孔隙比和土节点上作用的孔压在初始条件中输入，使用命令：*initial conditions，type=pore pressure。不考虑地下连续墙施工引起土体孔隙水压力的变化。此时孔压为静水压力，不存在超静孔压、孔压分布和重力场平衡，所以不会发生渗流。降水后土体中产生负的超静孔隙水压力，同时开挖后基坑内外产生水头差变化，开挖卸载在土体中也产生负的超静孔隙水压力，土中水在重力势(水头差)和压力势(超静孔压)的共同作用下发生渗流，在每步开挖结束之后，坑内外一定范围内土体的总水压力为负值，而且在开挖间歇期末坑内的超静孔隙水压力仍未消散完毕。

图1为地下连续墙水平位移变化图，从图中可以看出考虑时间效应计算结果与实际较相符。图2为墙体发生最大水平位移处的位移随时间产生的变化情况，当考虑时间效应时，有限元计算值为110.1mm，而墙体水平位移的检测值为101.46mm，与计算值仅相差8.64mm，可见计算结果与实际情况相符。而不考虑时间效应的计算值为82.3mm，与检测值相差19.16mm，明显小于检测值，与实际情况相差较多。可见，在软土地基中开挖深基坑有必要考虑软土的时间效应。

3 结 语

本文简单介绍了比奥(Biot)固结理论及其有限元解法，并对理论进行了推广，使其可以考虑土体的蠕变效应。基坑的时间效应是土体固结和蠕变共同作用的结果。应用大型有限元软件ABAQUS对工程算例及实例进行有限元分析。分析中考虑了土体固结及蠕变的耦合作用。由工程实例分析可知，考虑土体蠕变和固结耦合作用后得出的结果更接近于工程实际。

图1 墙体水平变形图

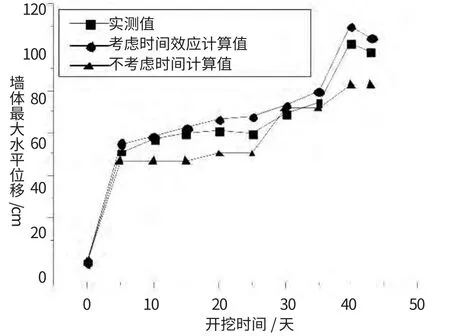
图2 墙体水平位移最大值处变化规律

[1]吴兴龙,朱碧堂.深基坑开挖坑周土体变形时空效应初探[J].土工基础,1999(13).

[2]Lee,F H.K Y Yong,K CNQuan and K T Chee(1998).Effects of corners in excavations:field monitoring and case histories[J].Journal of the Soil Mechanics and Foundations Division,ASCE,124(4).

[3]孙均.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999.

[4]高文华,杨林德.软土深基坑围护结构变形的三维有限元分析[J].岩土力学,2000(2).

[5]陈晓平,等.软土变形时效特性的试验研究[J].岩石力学与工程学报,2005(12).