一种辨识磨粒群分形无标度区的新算法

张怀亮 邹佰文 肖 雷

中南大学，长沙，410083

0 引言

机械设备在运转过程中产生的磨粒群包含丰富的摩擦磨损信息，对磨粒群特征进行提取，可用于设备的状态监测和故障诊断。研究表明，磨粒群在一定尺度上表现出分形特性，传统基于欧氏几何的参数无法准确描述磨粒群特征［1－2］。分形维数是表征磨粒群分形特性的一个重要参数，因而提高磨粒群分形维数的计算精度，对于磨粒群特征的提取和设备磨损状态监测有重要意义。由于产生机制复杂，磨粒群的分形自相似特性是近似或统计意义上的，即在一定尺度范围内的自相似，这个尺度范围即称为无标度区，在无标度区外讨论磨粒群的分形特性没有意义，因此，无标度区的准确辨识是磨粒群分形维数计算中必须解决的关键问题之一。

辨识无标度区的常用方法有以下几类：①基于r～N（r）（尺度～测度）双对数曲线的人工识别法［3］；②基于r～N（r）点对相关性检验的排序逼近法［4－8］；③基于三折线、曲线－直线－曲线、反 S等模型的模型拟合法［9－11］。人工识别法主观性强，排序逼近法在r～N（r）点对较多时计算量很大且较易出现局部最优，模型拟合法在模型的选取方面缺乏理论依据，应用时有一定局限性。因而，Yang等［12］利用无标度区一阶导数近似不变的特点提出应用聚类分析理论辨识无标度区的算法；Ji等［13］在此基础上结合K－means和点斜率误差法提高了算法的精度；王成栋等［14］根据无标度区二阶导数在0附近波动的特点提出了一种自动辨识方法，这类利用r～N（r）双对数曲线导数特点的辨识算法几何意义明确，计算量较小，但大多对初始值敏感，容易出现局部最优，可能导致辨识出来的无标度区虽然相关性检验参数符合要求，但并不是完整的无标度区，甚至不在真实无标度区内，即无标度区的局部最优。本文结合模拟退火和K－means算法对双对数曲线的一阶、二阶导数进行全局聚类，可有效避免陷入局部最优，从而提高磨粒群分形维数的计算精度。

1 磨粒群分形维数计算理论

磨粒群分散于设备的润滑油中，通过铁谱仪可将润滑油样中的磨粒群分离出来，制成铁谱片，经铁谱显微镜拍照成像，得到磨粒群的图像（图1a），原始图像背景复杂，通过背景去噪、阈值分割等图像预处理过程，得到磨粒群的二值图像（图1b），磨粒群分形维数的计算过程基于其二值图像。实际应用中，为保证状态监测数据的可比性，获取磨粒群图片时应遵守同样的取样倍数及视场选取规范。

分形维数的定义包括相似维、Hausdorff维、信息维、计盒维数等多种，其中，计盒维数（boxcounting dimension）由于其物理意义明确，便于程序化计算等优点，广泛应用于图像分形特征的表征。计盒维数的计算原理如下：将边长为r的方形网格覆盖所需测量的图形，测算与图形重叠的网格数目为测度N（r），不断改变网格边长，重复上述过程，得到一组不同尺度r下的测度N（r），那么计盒维数即为

图1 磨粒群原始图像及二值图像

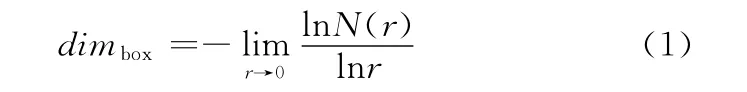
根据计盒维数的定义，磨粒群分形维数计算的一般过程如下：假设磨粒群图像的分辨率为M×M，以边长为r个像素的网格不断覆盖磨粒群图像并统计重叠网格数目N（r），其中r的取值范围为｛r｜1≤r＜ M／2，r＝1，2，4，…，2n｝［15］，根据r～N（r）点对序列绘出双对数曲线，将曲线中的直线部分作为无标度区间，在无标度区间内对r～N（r）点对进行线性回归，取分形维数D＝－α，其中α为回归直线的斜率。

在磨粒群分形维数的计算过程中，无标度区的辨识结果直接影响磨粒群分形维数的计算精度，辨识出来的无标度区若出现偏离、过短或过长等误差，会导致无法正确评估磨粒群的分形维数。而应用已有的无标度区辨识方法计算磨粒群的分形维数时，往往会出现局部最优的现象，如图2所示。图2中的数据点为磨粒群图像（图1）应用计盒维数算法得到的r～N（r）点对，A、B、C、D 4个区为不同的无标度区辨识结果，其中，A区、B区、C区数据点的线性相关系数均大于0.99，D区为0.97，将D区作为无标度区不严格，C区lnN（r）几乎为定值，即分形维数为0，显然不合理，B区虽然相关性符合要求，但长度太短，A区是较合理的无标度区。相对于A区、B区、C区为无标度区辨识过程中出现的两种典型的局部最优情况，即辨识结果虽在真实无标度区内，但长度过短和偏离真实无标度区，4个区内计算分形维数的结果为1.650、1.603、0.011、1.723，差异很大，所以，无标度区的准确辨识是磨粒群分形维数计算的关键环节。

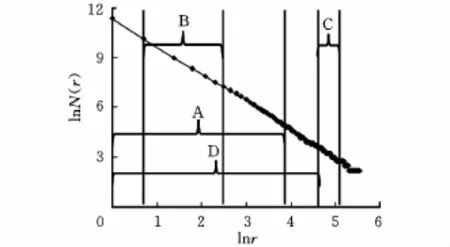
图2 无标度辨识中的局部最优

2 分形无标度区辨识新算法

为避免无标度区辨识算法陷入局部最优，将K－means聚类算法与全局搜索算法模拟退火算法相结合，从r～N（r）双对数曲线中准确辨识磨粒群无标度区。

2.1 模拟退火K－means算法

K－means算法是一种基于距离的聚类算法，该算法以距离为相似性指标，将观察对象分为k类［16］。基本过程如下：首先从研究对象中随机选择k个对象作为聚类中心，其余的对象根据它们到聚类中心的距离划分到最近的聚类。然后，以各聚类中所有对象的平均值作为新的聚类中心，重复上述划分过程，直到准则函数收敛。应用K－means算法对双对数曲线的导数进行聚类，可分离出无标度区，但是从K－means的聚类过程可以看出，算法对初始聚类中心的选择依赖很大，初始聚类中心选择不当，可能出现局部最优，将它应用到磨粒群无标度区的识别可能会出现无标度区过短等现象。

模拟退火算法是由Kirkpatrick提出的一种启发式、随机优化算法［17］。该算法与初始值无关，算法求得的解与初始解状态无关，具有渐近收敛性，已在理论上被证明是一种以概率1收敛于全局最优解的全局优化算法。因而，利用模拟退火算法能够弥补K－means算法依赖初始聚类中心的缺点，跳出局部最优。

模拟退火K－means算法以K－means聚类的结果作为模拟退火算法的初始解，通过随机改变聚类中某个元素的类别产生新解，目标函数为当前聚类划分的总类间离散度：

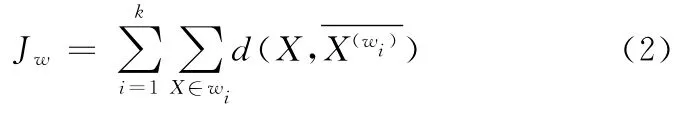
模拟退火K－means算法的实现步骤如下：

（1）将数据样本的K－means聚类结果作为初始解w，根据式（2）计算目标函数值Jw。

（2）初始化温度t0，t0＝Jw，初始化退火速度a和最大退火次数。

（3）在某一温度t，迭代进行步骤（4）～ 步骤（6），直到最大迭代次数跳到步骤（7）。

（4）通过随机改变一个聚类样本的当前所属类别产生新解w′，计算新的目标函数值J′w。

（5）判断J′w是否为最优目标函数值，若是，则保存聚类划分w′为最优聚类划分、J′w为最优目标函数值；否则跳到下一步。

（6）计算新的目标函数值与当前目标函数值的差ΔJ。判断ΔJ是否小于0：若ΔJ＜0，则接受新解，即将新解作为当前解；若ΔJ≥0，则根据Metropolis准 则，以 概 率 p（p ＝ eΔJ／（kt））接 受新解。

（7）判断是否达到最大退火次数，若是则结束算法，输出最优聚类划分；否则对温度t进行退火，返回步骤（3）继续迭代。

2.2 无标度区辨识新算法

在计算磨粒群分形维数时，辨识无标度区可简化为提取r～N（r）双对数曲线的直线部分。由于直线的一阶导数是常数，不随自变量的改变而变化，而曲线的一阶导数随着自变量改变而变化，直线的二阶导数为0，曲线的二阶导数不为0，利用这个性质，可以通过双对数曲线的一阶、二阶导数特点识别出曲线的线性部分，作为无标度区。实际计算得到的并不是连续的曲线，而是离散的r～N（r）点对序列，因而定义双对数曲线的一阶、二阶局部导数分别为

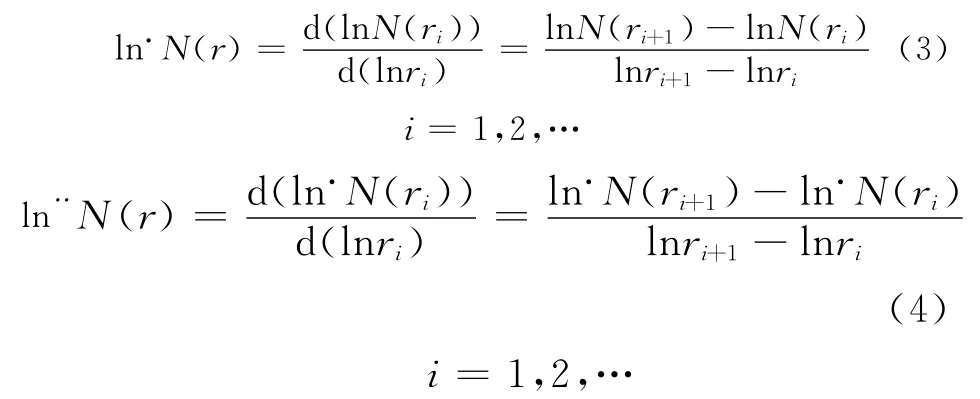
理论上，无标度区内点的一阶局部导数为常数，但磨粒群并不是完全理想的分形图形，所以实际计算中，无标度区内点的一阶局部导数在一个常数附近做微小波动，而无标度区外点的波动幅度较大；无标度区内点的二阶局部导数在0附近作微小波动，而无标度区外的点偏离0较远。因而，应用模拟退火K－means算法对双对数的一阶局部导数聚类，分离出无标度区的大致范围，对其二阶局部导数聚类，辨识出无标度区的准确区间。磨粒群分形无标度区辨识的新算法如下：

首先，应用模拟退火K－means算法对磨粒群分形维数计算中的双对数曲线进行一阶导数聚类，结果如图3a所示。经过聚类，双对数曲线一阶局部导数被分为两类（图中ln·N（r）group1和ln·N（r）group2），两类离散点交错分布，将初始的双对数曲线分成了许多段区间（图3a中竖线分割），各区间长短不一。其中，当lnr较大时，出现了多段一阶导数连续为0点区间，这是由于采用计盒法计算时，当盒子尺寸较大时，盒子尺寸的改变量相对盒子本身尺寸很小，覆盖磨粒群的盒子个数并不随盒子尺寸的变化而改变，这些区间不符合无标度区的定义，应予以剔除。剩下的区间中，多为较短的区间，甚至只有一个点，由于磨粒群的分形无标度区一般较宽，因而选取包含连续点最多的区间作为无标度区，识别结果如图3b所示。需要指出的是，虽然从图3b上看，被剔除的区间较短，但由于双对数曲线的压缩特性，实际被剔除的点的数量是很大的，而这些点都明显不属于无标度区，说明计算过程中r的取值范围可以进一步缩小以提高分形维数计算效率。在磨粒群分形维数计算过程中，如果对这些点不加以剔除，计算结果将出现很大的偏差。

通过上述的识别过程，无标度区的大概范围已被确定，但区间还存在一些波动相对较大的部分（一阶导数右端），为精确确定无标度区，还需进一步剔除这些点。由于一阶导数在常数附近波动，其二阶导数应该在0附近作微小波动，若二阶导数偏离0的幅度较大，则表明其一阶导数波动剧烈，因而，对其二阶导数进行模拟退火K－means联合聚类，结果如图3c所示，一阶导数的波动在二阶导数上表现得更明显，与一阶导数类似，通过聚类，区间分割，选取包含连续点数最多的区间，最终得到的无标度区如图3d所示。磨粒群无标度区识别结果中，双对数曲线二阶导数在0附近作微小起伏，说明双对数曲线在该区间内接近直线，即磨粒群的无标度区。

对识别的无标度区内的点进行线性回归，相关系数R＝0.9994，说明无标度区内r～N（r）双对数曲线线性相关性很强，符合无标度区的定义。同时，整个辨识磨粒群分形无标度区的过程中，未出现辨识结果过短或落在无标度区外等局部最优现象，在保证通过相关性检验的前提下尽可能选取了较长的区间，有效地避免了陷入局部最优。对无标度区内的点进行最小二乘拟合，即可得到直线的斜率α，根据盒维数的定义，取D＝－α，作为磨粒群的分形维数。

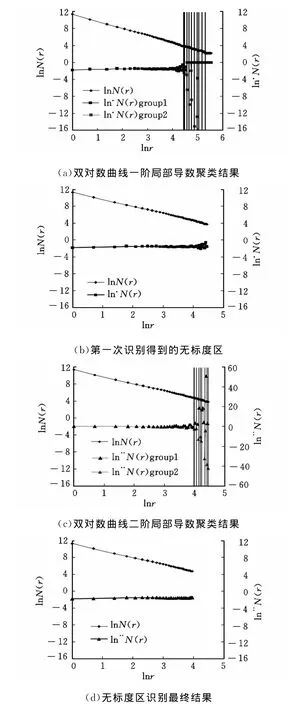
图3 磨粒群分形无标度区辨识过程

2.3 方法检验及结果分析

为检验新方法对无标度区识别的准确性及精度，选取Koch曲线、Sierpinski三角形、Sierpinski方毯三个已知理论分形维数的图形作为测试对象，三个图形的大小一致，采用计盒法获取三个图形的r～N（r）双对数曲线，利用新方法识别相应的无标度区，对无标度区内的点进行最小二乘拟合，确定图形的分形维数。同时，为了对比研究本文无标度区识别方法的精度，同时用人工识别法和文献［14］提出的二阶导数法对三个图形无标度区进行了识别，计算结果如表1所示，图4示出了三种方法计算结果与理论值的误差。

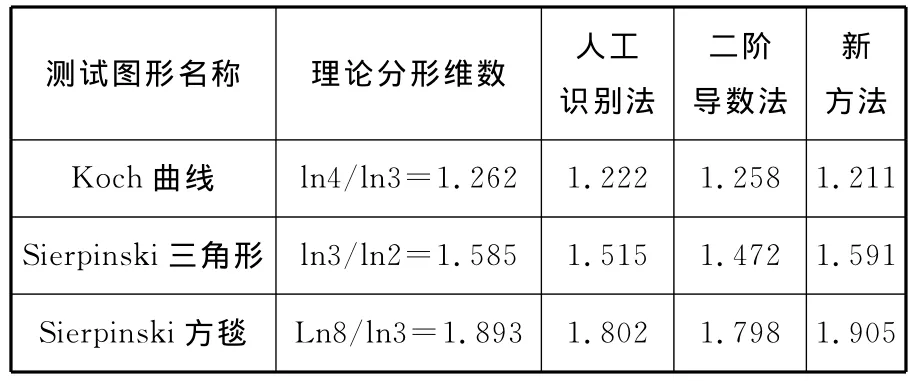
表1 测试图形分形维数计算结果

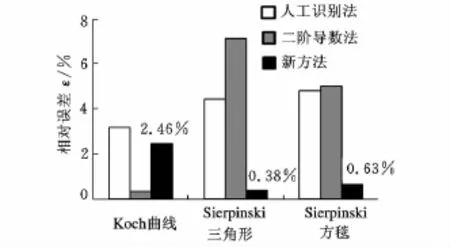
图4 三种无标度区识别方法相对误差

应用新方法辨识三个图形无标度区的过程中均出现局部最优现象，图4表明，人工识别法在三个图形的无标度区识别中都取得了较好的效果，平均误差在3%～5%之间，但是人工识别法需与计算机进行交互操作，无法进行自动识别，且不同观察者一般得到不同的结论，主观性强；二阶导数法对Koch曲线的识别效果很好，但对其他两个图形的无标度区识别效果较差；本文提出的识别方法虽对Koch曲线的识别效果与人工识别法效果相当，但对Sierpinski三角形和Sierpinski方毯的识别误差均在1%以下，由于Sierpinski三角形和Sierpinski方毯的特点与磨粒群的特点相似，都是一种多孔结构，因而应用本文提出的方法对磨粒群分形无标度区的识别是合理的，分形维数的计算结果是可信的。

3 磨粒群的分形无标度区辨识

为分析新方法对磨粒群无标度区的辨识能力，应用新方法计算了正常磨损、切削磨损、滚动疲劳磨损、滚动和滑动复合磨损及严重滑动磨损的磨粒群分形维数，磨粒群图片来自文献［18］，图片大小为400像素×400像素，盒子尺寸增长方式为 ｛r｜1≤r＜M／2，r＝1，2，4，…，2n｝，计算程序基于MATLAB开发，计算机CPU主频为3.00GHz，计算结果如表2所示，其中，无标度区中的数值范围表示r～N（r）双对数曲线中识别的无标度区取点范围。

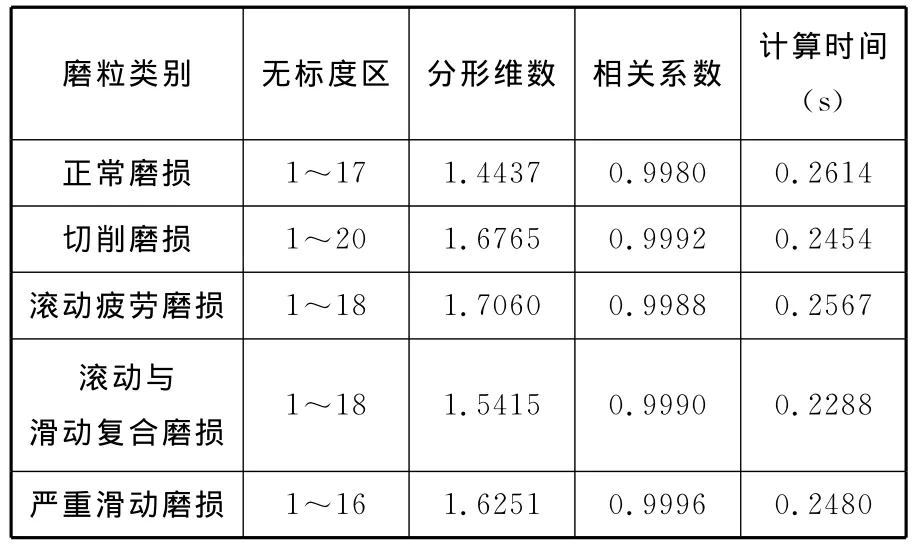
表2 应用新方法计算磨粒群分形维数结果

计算结果表明，在图片大小为400像素×400像素，盒子尺寸增长方式为1，2，4，…，2n时，磨粒群的分形无标度区大约为1～20个点之间，取此区间内的点对进行拟合，可以得到较精确的磨粒群分形维数，这段区间内，点对的线性相关系数大于0.99，同时区间长度占整个双对数曲线的50%左右，未出现无标度区辨识的局部最优。另外，试验中不同磨损状态的磨粒群分形维数差异较大，从1.44到1.71，这表明磨粒群的分形维数可作为摩擦副磨损状态识别的一个判据。新算法对给定条件下磨粒群无标度区进行识别所耗用CPU时间约为0.24s，同样条件下应用文献［8］、［13］和［14］提出的方法对磨粒群无标度区进行识别所用CPU 时间分别为0.3s、0.25s、0.8s左右，相对于已有算法，新算法在保持较高的无标度区识别精度的同时，识别效率也略有提高。

4 结论

（1）基于模拟退火K－means算法提出了一种辨识磨粒群分形无标度区的新算法，新算法能有效地避免无标度区辨识过程中陷入局部最优，从而准确辨识磨粒群的分形无标度区，提高分形维数的计算精度。

（2）新算法对磨粒群图像、Sierpinski方毯等多孔状图形无标度区辨识精度高，辨识得到的磨粒群分形无标度区较宽，区间内点对的线性相关性好。

［1］Podsiadlo P，Stachowiak G W.Scale－invariant Analysis of Wear Particle Surface Morphology：II.Fractal Dimension［J］.Wear，2000，242（1／2）：180－188.

［2］Yuan C Q，Li J，Yan X P，et al.The Use of the Fractal Description to Characterize Engineering Surfaces and Wear Particles［J］.Wear，2003，255（1／6）：315－326.

［3］郭中领，符素华，张学会，等.土壤粒径重量分布分形特征的无标度区间［J］.土壤通报，2010，41（3）：537－541.Guo Zhongling，Fu Suhua，Zhang Xuehui，et al.Scale－free Domain of Fractal Characteristic of the Soil Particle－size Distribution［J］.Chinese Journal of Soil Science，2010，41（3）：537－541.

［4］Tang G J，Du B Q，Wang S L.Scaleless Band Automatic Identification for Fractal Fault Diagnosis of Rotor System［J］.J.Power Eng.，2009，29：440－444.

［5］秦海勤，徐可君，江龙平.分形理论应用中无标度区自动识别方法［J］.机械工程学报，2006，42（12）：106－109.Qin Haiqin，Xu Kejun，Jiang Longping.Fractal Scaleless Band Automatic Identification for Fractal Theory Application［J］.Chinese Journal of Mechanical Engineering，2006，42（12）：106－109

［6］Fang Zhijun，Zhou Yuanhua，Zou Daowen，et al.Efficient Scheme for Determining Fractal Scaleless Range［J］.Journal of Infrared and Millimeter Waves，2004，23（5）：321－324.

［7］党建武，施怡，黄建国.分形研究中无标度区的计算机识别［J］.计算机工程与应用，2003，39（12）：25－27.Dang Jianwu，Shi Yi，Huang Jianguo.The Identification of Fractal Scaleless Band in the Study of Fractal with Computers［J］.Computer Engineering And Applications，2003，39（12）：25－27.

［8］巫兆聪.分形分析中的无标度区确定问题［J］.测绘学报，2002，31（3）：240－244.Wu Zhaochong.Determination of Fractal Scaleless Range［J］.Acta Geodaetica Et Cartographica Sinica，2002，31（3）：240－244.

［9］庞茂，吴瑞明，谢明祥.关联维数快速算法及其在机械故障诊断中的应用［J］.振动与冲击，2010，29（12）：106－109.Pang Mao，Wu Ruiming，Xie Jingxiang.Improved Correlation Dimension Algorithm with Its Application to Mechanical Fault Diagnosis［J］.Journal of Vibration and Shock，2010，29（12）：106－109.

［10］栾海军，汪小钦.多源遥感影像分形特征分析［J］.遥感信息，2010，3：7－12.Luan Haijun，Wang Xiaoqin.Fractal Features Analysis of Multi－source Remote Sensing Images［J］.Remote Sensing Information，2010，3：7－12.

［11］蔡金华，龙毅，毋河海，等.基于反S数学模型的地图目标分形无标度区自动确定［J］.武汉大学学报（信息科学版），2004，29（3）：249－253.Cai Jinhua，Long Yi，Wu Hehai，et al.Automatic Determination of Fractal Non－scale Interval of Map Objects Based on Inverse‘S’Mathematical Model［J］.Geomatics and Information Science of Wuhan University，2004，29（3）：249－253.

［12］Yang H Y，Ye H，Wang G Z.Identification of Scaling Regime in Chaotic Correlation Dimension Calculation［C］／／3rd IEEE Conferenceon Industrial Electronics and Applications.ICIEA，2008：1383－1387.

［13］Ji C C，Zhu H，Jiang W.A Novel Method to Identify the Scaling Region for Chaotic Time Series Correlation Dimension Calculation［J］.Chinese Science Bull，2011，56：925－932.

［14］王成栋，凌丹，苗强.分形无标度区的一种自动识别方法［J］.计算机工程与应用，2012，48（6）：9－12，27.Wang Chengdong，Ling Dan，Miao Qiang.Automatic Identification Method of Fractal Scaling Region［J］.Computer Engineering and Applications，2012，48（6）：9－12，27.

［15］Ajay K B，Jibitesh M.On Calculation of Fractaldimension of Images［J］.Pattern Recognition Letters，2001，22（6）：631－637.

［16］Kalyani S，Swarup K S.Particle Swarm Optimization Based K－means Clustering Approach for Security Assessment in Power Systems［J］.Expert Systems with Applications，2011，38（9）：10839－10846.

［17］Vasan A，Raju K S.Comparative Analysis of Simulated Annealing，Simulated Quenching and Genetic Algorithms for Optimal Reservoir Operation［J］.Applied Soft Computing，2009，9（1）：274－281.

［18］金元生.铁谱技术及在磨损研究中的应用［M］.北京：机械工业出版社，1991.