基于CFD的VIV刚性圆管纵横比与雷诺数的作用效应

刘桢兵

(中国船级社 舟山办事处，浙江 舟山316000)

0 引 言

海洋天然气和石油能源作为陆地能源的首要替代品，正日益受到全球科学界的重视，面对大规模的开采，首当其冲的问题是克服流体介质所带来的影响。作为一种圆管结构，面对复杂海况，其所受载荷的状况以及附近流场的分布备受关注。圆管在洋流作用下会产生涡激振动，并在流动方向的2 个切点呈现周期性分离，最后在圆管的背流面产生涡的脱落，形成涡街现象［1］。以往的研究往往是针对二维模型进行数值模拟，早期的Koopman 在低雷诺数下发现了涡脱落频率与振动频率的吻合条件［2］，随后的 Ayoub ＆Karamcheti［3］针对三维流场提出了许多研究性和工程实际应用上的宝贵结论，丰富的实验数据极大地带动了这一领域的发展。为了更好地观察两端固定于刚性壁端的圆管方向各个切面的流场信息，本文采用三维模型进行分析，因此引入了圆管长度/圆管半径纵横比Aspect Ratio 这个概念，即AR=L/D，二维模型所模拟的效果反映的是AR 趋向无限值。本文使用AR 均为模拟长度与直径具有可比性的情形。作者根据有限体积法，利用Fluent，Gambit，Matlab 以及Tecplot 等软件对多种模型和流场情形进行数值模拟，并得出最终结论。

1 模型构建以及方法论

1.1 计算模型

图1 为模拟的三维流场图，表1 对流场图的边界和介质进行说明和阐述，表2 为Gambit 网格划分后和优化后的网格数目情况，经过与实验数据及先前研究结果比对(见1.2 中无限AR 下的模拟结果)该模型模拟结果符合要求。其中周界尺寸如下:

X－方向:上游长度(左)=5D=5cm;下游长度(右)=25D=25cm。

Y－方向:流场宽度(前后)=5D=5cm。

Z－方向:流场深度(圆管长度)=4D/8D/10D=4cm/8cm/10cm。

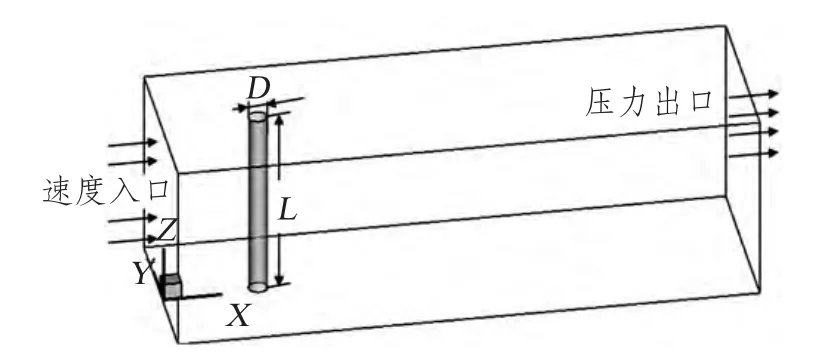
图1 三维模型图Fig.1 3D model

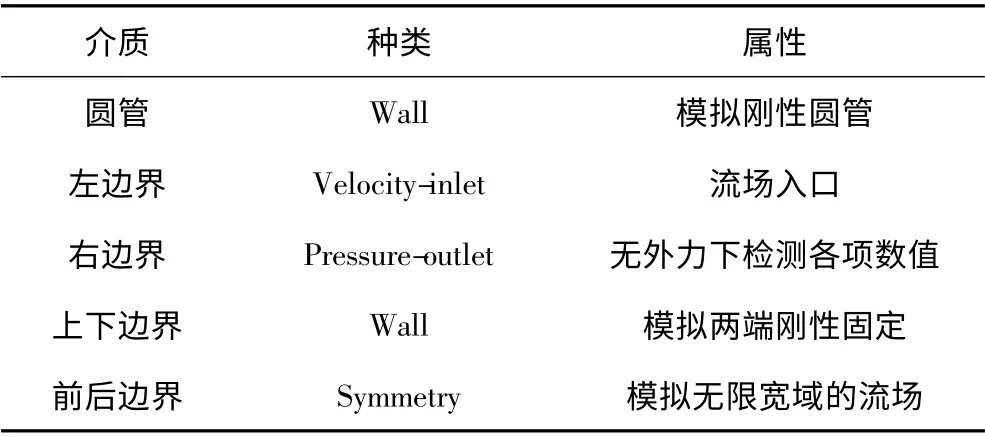
表1 边界类型Tab.1 Boundary type

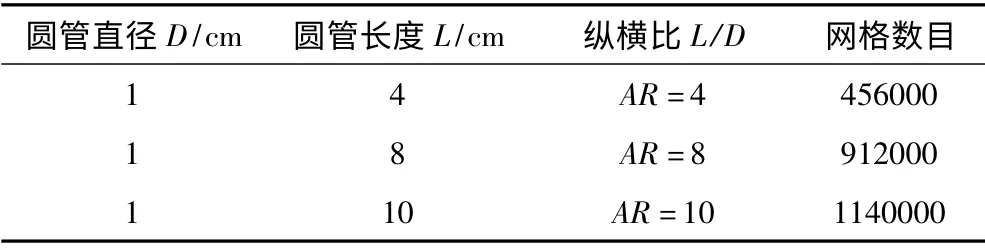
表2 不同纵横比下三维模型网格数目Tab.2 Mesh number of 3D model under different aspect ratio

表3 不同雷诺数下对应的流速Tab.3 Flow speed under different Reynolds number

1.2 数值计算方法

使用Fluent 12.1 对三维流场进行模拟运算，遵循纳维－斯托克斯方程和连续方程这两大守恒方程，针对Re 在300 以内的情况均使用层流粘性模型

阻力系数和升力系数的数值取决于圆管表面粘性状态以及作用力分布，根据以下公式计算所得

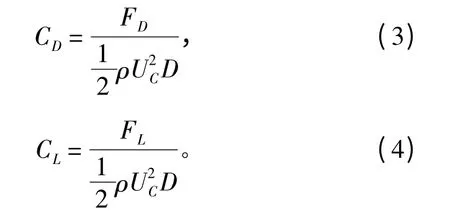
式中FD和FL为作用于圆管上的单位长度受力值，具体计算公式如下

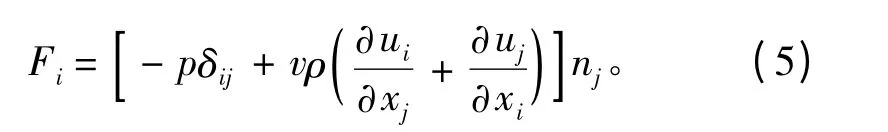
斯特罗哈数反映涡脱落现象，主要基于升力系数的主频率

层流经过圆管后的涡间距是圆管的伴流波长来定义的，根据式(7)计算所得

式中:U 为名义流速;fc为指涡脱落频率;Cd，Cl 以及fc对应的数值可在Fluent 中的FFT 功能获取。

1.3 CFD 模型系数及参数设置

Versions:Fluent 12.1－3D

Solver:Pressure based

Formulation:Implicit

Time model:Unsteady

Unsteady formulation:2nd－order implicit

Viscous model:Laminar ＆ Large Eddy Simulation

Pressure-Velocity Coupling:SIMPLE

Discretization of Pressure:Standard

Discretization of Momentum:2nd－oder upwind

Residual Absolute Criteria:1.0e－3

Reference Values:Area(L* D m* m)，Density(1 024.73kg/m3)，Length(D)，Temperature(288.16K)velocity(Given in Tab.3)and viscosity(0.00 108 Ns/m2)

2 计算实例

2.1 模拟无限AR 下的流场

在Re=100 下的无限AR 三维数值模拟计算如图2和图3所示。经过数值和涡街图样比较，与B.N.Rajani et al.［4］，CHANG et al.［5］和BAI et al.［6］结果基本一致，因此可用于本文所用模型计算。

图2 3D 切片示意图Fig.2 3D－division slices

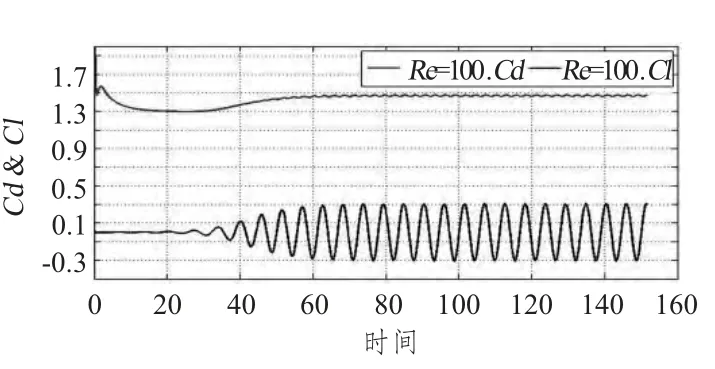
图3 阻力系数和升力系数变化图Fig.3 Time history curves of drag coefficients and lift coefficients

2.2 数值模拟计算

切面位置取3 处，分别为中部和端部1/8L(AR=4)，1/16L(AR=8)，1/20L(AR=10)，切面图如图4 ～图6所示，频率分布与关系曲线如图7 ～图9所示，阻力系数与升力系数的对比如图10所示，处理后数据结果如表4所示。

图4 AR=4:不同Re 下切面图(Ratio=4)Fig.4 AR=4:3D－division slices under different Reynolds number(Ratio=4)

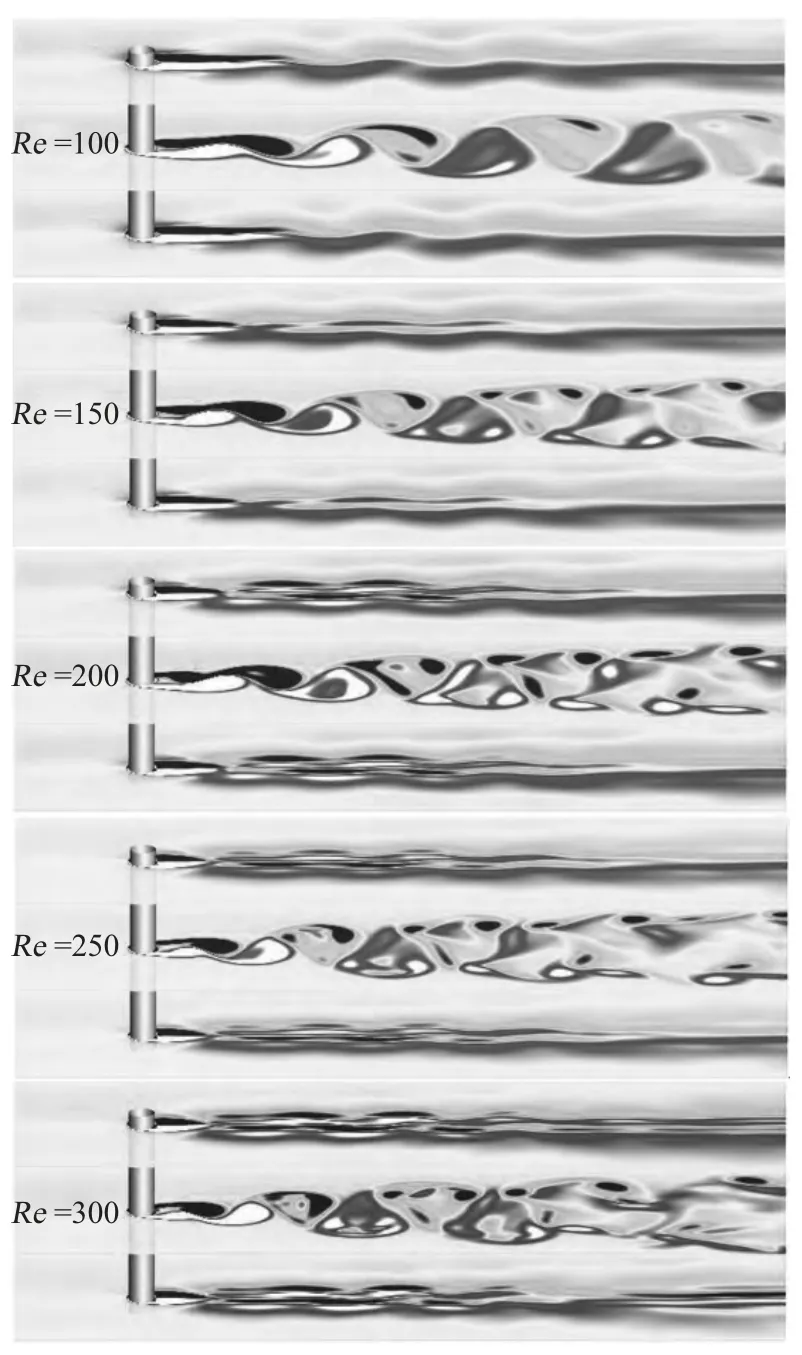
图5 AR=8:不同Re 下切面图(Ratio=8)Fig.5 AR=8:3D－Division slices under different Reynolds number(Ratio=8)

图6 AR=10:不同Re 下切面图(Ratio=10)Fig.6 AR=10:3D－Division slices under different Reynolds number(Ratio=10)

图7 AR=4:涡脱落频率分布图及雷诺数－斯特罗哈数对应关系图Fig.7 AR=4:Vortex shedding frequency map and Re－St relational graph

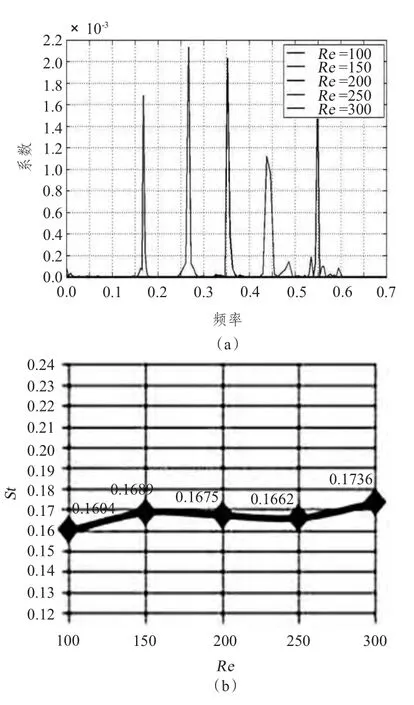
图8 AR=8:涡脱落频率分布图及雷诺数－斯特罗哈数对应关系图Fig.8 AR=8:Vortex shedding frequency map and Re－St relational graph

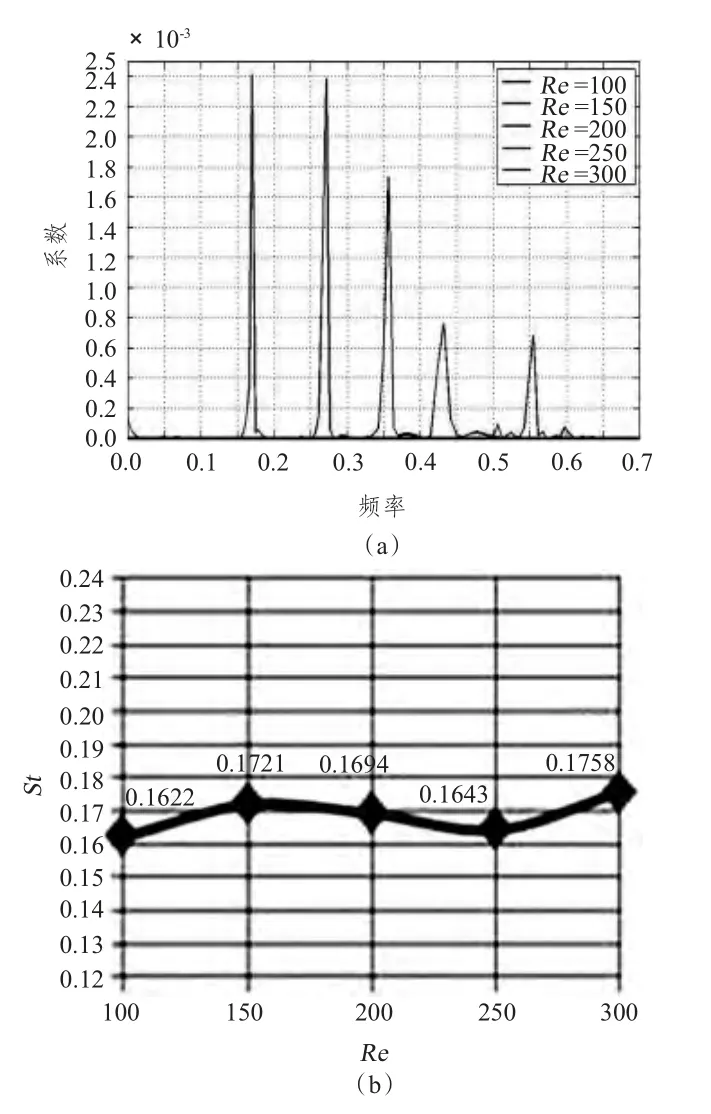
图9 AR=10:涡脱落频率分布图及雷诺数－斯特罗哈数对应关系图Fig.9 AR=10:Vortex shedding frequency map and Re－St relational graph

表4 Fluent 软件综合处理后数据结果Tab.4 Data ＆ result analyzed by Fluent

图10 不同AR 与Re 下阻力系数和升力系数的对比图Fig.10 Comparison diagram of drag coefficients and lift coefficients under different AR and Re

3 结 语

从上述数据图中可以发现，在相同纵横比下，涡脱落的频率随着雷诺数的增加呈现递增趋势，对以往的实验数据和模拟结果进行佐证。在相同雷诺数下，小的纵横比具有更大的涡脱落频率，涡的变化形态更为复杂。阻力系数随着雷诺数的增加呈现递减趋势，在低纵横比工况下尤为明显，相同雷诺数下，以Re=200 为分界点，随纵横比增加由递减转而递增。升力系数随雷诺数也呈现相同的递减趋势，仅在雷诺数小于200 区域内出现不稳定过渡状况，随着雷诺数增加至200 后，变化趋势趋于明显，相同雷诺数下，纵横比与升力系数成正比。由此发现，层流模式下，流场基本属于稳定形态，唯独Re=200 是一个特殊临界值，而伴流长度也在该处产生趋势变化，这也是为何以往研究往往会涉及这一特殊工况，在无限AR 工况下，该雷诺数下的涡街极为明显，而当纵横比被限定后，往往会有不可预见的变化产生，值得发掘并利用，对于近海开采以及SPAR 平台的油气开采具有指导意义。在今后的发展中，对洋流多自由度激励工况以及圆管的柔性运动要加以研究，以获得更好的工程应用经验。

［1］ARVIND S K，SHANKAR K V V，VIGNESH S．Renewable energy from vortex induced vibrations in a slow moving fluid［C］．International Conference on Environmental Engineering and Applications，2010．

［2］KOOPMAN G H．The vortex wakes of vibrating cylinders at low Reynolds numbers［J］．J．Fluid Mech，1967，28:501－512．

［3］ALFRED A，KARAMCHETI K．An experiment on the flow past a finite circular cylinder at high subcritical and super critical Reynolds numbers［J］．J．Fluid Mech．1982，118:1－26．

［4］RAJANI B N，KANDASAMY A，SEKHAR M．Numerical simulation of laminar flow past a circular cylinder［J］．Applied Mathematical Modelling，2009，33:1228－1247．

［5］CHANG Shu-ping，WANG Yong-sheng，PANG Zhi-yang．Numerical simulation of flow around circular cylinder using SST DES model［J］．Ship Science and Technology，2009，31(2):30－33．

［6］BAI Hua，LI Jia-wu，XIA Yong．Numerical simulation and control measures of flow around circular cylinders at low reynolds number［J］．Journal of Architecture and Civil Engineering．2010，27(4)．