混响干扰下的潜艇目标尺度识别

董仲臣，李亚安，刘望生

(1.西北工业大学 航海学院，陕西 西安710072;2.中国人民解放军91388 部队，广东 湛江524022;3.浙江理工大学 机械与控制学院，浙江 杭州310018)

0 引 言

鱼雷自导系统在工作时，有2 种海洋背景干扰［1］:一种与鱼雷发射信号无关，由鱼雷自噪声和海洋环境噪声形成的噪声;另一种与鱼雷发射信号有关，是海洋中大量无规则散射体对入射信号产生的散射波在接收点叠加而形成的混响［1-2］。对于鱼雷主动自导系统，在浅海环境下，混响成为主要的背景干扰，严重影响了自导系统的性能［1，3］。并且，潜艇可以使用各种类型的水声对抗器材对鱼雷的攻击实施对抗，大大降低了鱼雷的攻击能力。所以，鱼雷自导系统应该具备混响干扰下对潜艇目标和诱饵进行识别的能力，从而能正确地对真实目标进行打击［4］。

本文在建立混响条件下潜艇目标亮点模型的基础上，提出一种混响干扰下潜艇目标识别方法。该方法用自身多普勒抑制技术对带有混响的回波进行混响抑制，并采用MUSIC 算法对潜艇目标亮点进行方位估计，从而实现对潜艇目标的尺度识别。仿真结果表明，该方法能够很好地实现对潜艇目标的尺度识别。

1 混响干扰下的潜艇目标亮点模型

1.1 混响信号仿真

为了体现鱼雷运动对混响信号的影响，本文对单元散射混响模型［2，5］进行改进，把产生混响的海底划分成若干散射单元，每个散射单元都能散射出具有一定多普勒频移的散射波，则混响信号等于发射信号通过各个散射单元产生响应的总和。利用该方法进行仿真，可以根据需要把散射单元划分到足够小，因此鱼雷相对每个散射单元的多普勒频移相同，从而比较准确的体现鱼雷运动对混响信号的影响。散射单元的划分如图1所示。

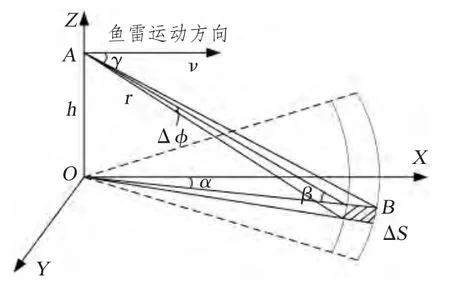
图1 散射单元划分示意图Fig.1 Scatteringunit classification diagram

t 时刻，对混响有贡献的区域为如图1 中圆环。把此圆环分割成若干散射单元，鱼雷到散射单元的距离为r，散射单元的面积为ΔS，散射单元对应的圆心角为Δφ。鱼雷以速度v 沿着X 轴运动，鱼雷距离海底为h，散射单元与鱼雷速度方向的夹角为γ，相对于鱼雷的仰俯角为β，与X轴的夹角为α。

散射单元的面积ΔS 可由式(1)求得:

其中:AB2=cτ/2，r=(c(t－τ))/2，τ 为鱼雷主动声脉冲宽度。

第i 个散射单元的响应为:

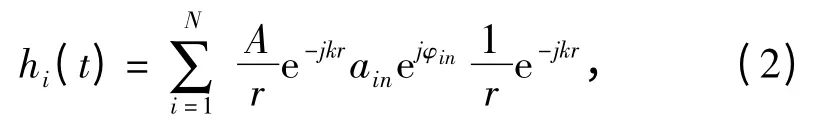
对式(2)进行整理得:

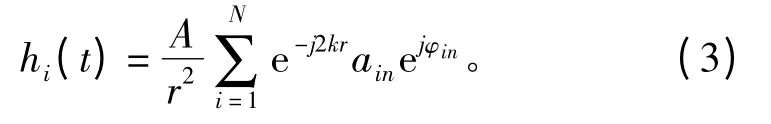
式中:A 为发射信号强度;N 为单元内散射体的数量;k 为波数，k=2πf/c;为散射体的散射系数，随机振幅ain和随机相位φin都按高斯分布［5］。

N 可由式(4)求得:

其中ρ 为单位面积散射体的数量。

考虑鱼雷运动带来的多普勒频移时，假定散射单元足够小，所以对于每个散射单元，散射波的多普勒频移相同，多普勒频移为:

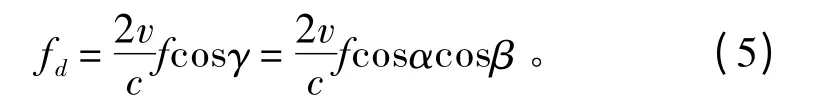
式中:f 为入射波频率;c 为水中声速。当海区条件为浅海时，鱼雷到海底的距离h 很小，所以此时把β近似为0 可以简化仿真，则式(5)变为:

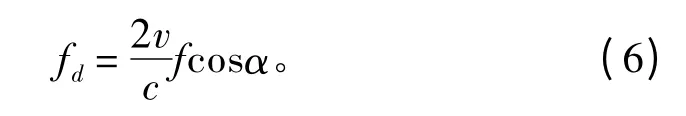
设鱼雷发射的主动信号为s(t)，在每个散射单元上产生的混响为:

其中⊗为卷积运算。

则t 时刻产生的混响为发射信号通过各个系统的叠加:

式中:Ns为散射单元的数量;ψ 为鱼雷自导系统方位角束宽。

1.2 潜艇目标亮点模型

理论分析和实验结果表明，在高频情况下，任何一个目标的回波都是由若干个子回波迭加而成，而每个子回波都可认为是从某个散射点发出的，这个散射点就是亮点。亮点可以真实存在，也可以是等效。这样，任何一个目标都可以等效成若干个亮点的组合，每个亮点产生一个回波，所以，目标总的回波是这些亮点回波的迭加［6-7］。

在目标回波中有3 个重要的特征，即目标回波的时间展宽、目标回波的亮点起伏和目标回波空间方位分布。这3 个特征是对目标进行识别的重要依据，且在实验中已证实了它们的存在。所以，1 个完整的目标回波模型可以由幅度因子、时延和相位跳变3 个参量确定［6-8］。单个亮点的传递函数可表示为:

式中:r 为鱼雷到目标亮点的距离;Ai(r，θ，ψ)为该亮点回波的幅度，它与目标的距离r 和声波入射方向，即照射角θ 和俯仰角ψ 有关;τi为该亮点的时延，由等效声中心相对于某个参考点的声程决定，且是θ 的函数;ω(v)为由于目标的相对运动，造成回波的中心频率与入射波的中心频率相差一个多普勒频移;φ 为回波形成时的相位跳变。

因此，潜艇目标总的传递函数为:

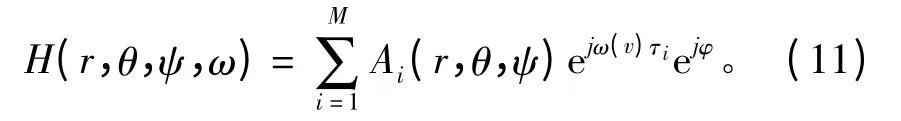
其中M 为目标亮点的个数。

设鱼雷发射的窄带脉冲信号为

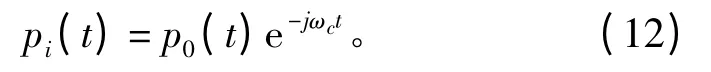
式中:ωc为载频;p0(t)为包络，它只在脉冲持续时间内有值。

无论目标多么复杂，在远场中散射波都以exp(jkr)/r 的规律扩展，k 为波数。取目标亮点个数为3，得到的回波为:

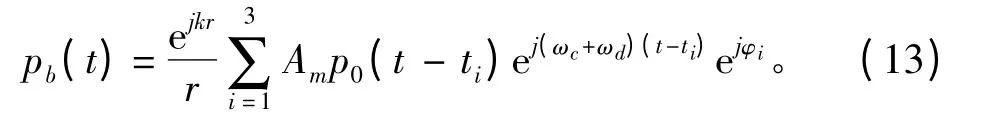
其中ωd为潜艇和鱼雷相对运动产生的多普勒频移。由于鱼雷已经对自身运动产生的多普勒进行了补偿，因此只需考虑潜艇运动产生的多普勒频移:

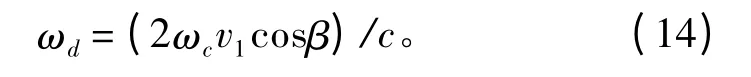
其中v1为潜艇运动速度。

对于潜艇上曲率面积较小的反射点，由于目标强度较小，仿真时可以随机噪声n(t)来代替。则式(14)变为:

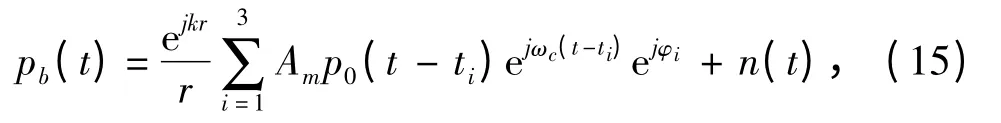
亮点回波的幅度为

假设声波以照射角θ入射时，由于鱼雷的声脉冲发射周期很短，可认为在一个声脉冲发射周期内鱼雷与潜艇的相对距离不变。则第i 个亮点的时延为:

式中:r 为鱼雷与潜艇距离，即鱼雷与代表舰首的亮点距离;θ 为照射角;li为亮点与舰首的距离。

由于入射声波遇到亮点后反射，在回波信号中引入相位跳变φi，它是一个在(0，2π)中均匀分布的随机变量，则混响干扰下的潜艇目标亮点回波信号为:

2 混响干扰下的目标尺度识别

对于带有混响信号的回波信号，本文先用自身多普勒抑制技术行混响抑制，然后采用MUSIC 算法，对潜艇的目标亮点进行方位估计，从而实现对潜艇目标的尺度识别［9-11］。

2.1 混响抑制

对鱼雷来讲，自身多普勒抑制技术是行之有效的抗混响技术，它主要是利用混响信号与目标回波多普勒频移的差异来对混响进行抑制。

分布于海洋中和界面上的散射体都是混响的来源。这些散射体都有一个共同特征，即均为固定不动或者运动速度很小。因此在浅海环境下，混响信号与目标回波多普勒频移量的差别是抗混响可利用的信息。

混响信号的频率与速度为0 时的目标回波频率相近，而鱼雷所攻击的目标一般具有一定的运动速度，所以，利用混响频率与目标回波频率的差别设计一多普勒门，当接收信号频率未达到一定范围时，多普勒门关闭，使混响难以通过，从而达到抑制混响的目的。多普勒门的实现可以通过设计特性频率响应的滤波器来实现。

2.2 目标尺度识别

为了对混响抑制后的潜艇目标回波进行方位估计，现 采 用 MUSIC 算 法 ( Multiple Signal Classification Algorithm)来实现潜艇目标的尺度识别。MUSIC 算法通常又称多重信号分类方法，是根据接收数据的协方差矩阵，分离出信号子空间和噪声子空间，利用信号方向向量与噪声子空间的正交性，来构成空间扫描谱，实现信号的方位估计。

对于一个由M 个阵元组成的已知任意集合形状矩阵，假设有D(D ＜M)个远场窄带信号(中心频率为f0)，信号源从D 个方向ΘD=［φ1，φ2，…，φD］入射到该基阵。这M 个阵元的接收信号写成矩阵形式为

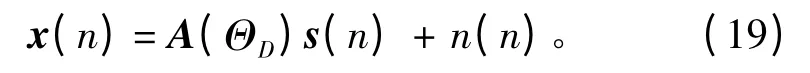
式中:A(ΘD)=［a(φ1)，a(φ2)，…，a(φD)］为M ×D 维阵列流行矩阵;s(n)=［s1(n)，s2(n)，…，sD(n)］为D ×1 维信号源向量;n(n)为M ×1 维噪声向量。

数据协方差矩阵可以表示为

其中Rs和Rn分别为D ×D 维信号协方差矩阵与M ×M 维噪声协方差矩阵，即

对协方差矩阵Rx进行特征分解，可将

式中:Λ 为降序排列的特征值构成的对角阵;E=［Es，En］为对应的特征值，Es与En分别是由较大的D 个特征值和较小的M－D 个特征值对应的特征向量组成的信号子空间和噪声子空间。

阵元域MUSIC 方位谱函数为

其中φ ∈Θ，Θ 表示观察扇面。

让φ 在观察扇面Θ 内扫描，计算出式(24)在各扫描方位对应的函数值，该函数出现峰值的方位，即为信号方位估计值。3 个亮点的回波对鱼雷来说相当于3 个信号源，根据窄带阵元域MUSIC 方位估计原理，对潜艇目标亮点进行方位估计，从而实现对潜艇目标的识别。

3 仿真结果及分析

3.1 计算机仿真

假设鱼雷自导系统发出的信号为梯形脉冲信号，仿真计算潜艇目标3 个亮点的回波信号的方位谱。仿真条件如下:鱼雷发射信号载波频率为30 kHz，采样频率为200 kHz。鱼雷到潜艇的距离为500 m，舰桥和舰尾到舰首的距离L1和L2分别为75 m 和125 m，潜艇速度为5 m/s，声速1 500 m/s。接收基阵为半波长间隔均匀线列阵，阵元个数M=10，混响为主要背景干扰，单位面积散射体的个数ρ=1。

自身多普勒抑制所用的滤波器的频率响应如图2所示，混响抑制效果如图3所示。

图2 滤波器的频率响应Fig.2 The frequency response of the filter

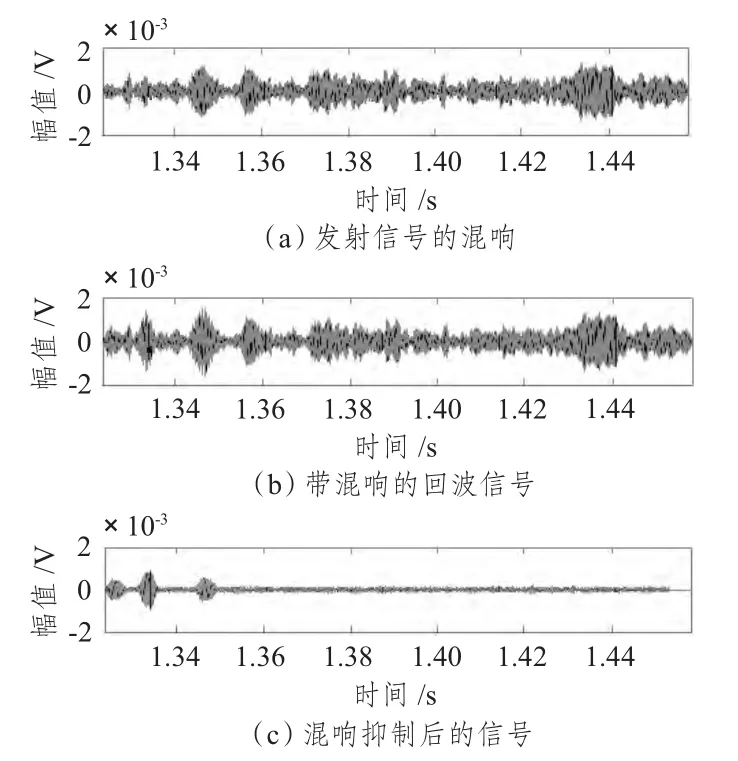
图3 混响抑制效果Fig.3 Effect of reverberation suppression

把混响抑制后的回波信号，用MUSIC 算法进行目标亮点的方位估计。取不同的照射角θ 进行仿真，仿真结果如图4 ～图7所示。

图4 θ=0° 时方位谱Fig.4 The azimuth spectrum of θ=0°

图5 θ=10° 时方位谱Fig.5 The azimuth spectrum of θ=10°

3.2 结果分析

当鱼雷相对潜艇的照射角θ 取不同值时，仿真产生的潜艇亮点回波的方位谱不同。图4 是θ=0°时的方位谱，此时方位谱函数有1 个峰值，无法对3 个亮点进行识别。图5 是θ=10°时的方位谱，此时方位谱函数有2 个峰值，只能对2 个亮点进行识别。图6 是θ=20°时的方位谱，此时方位谱函数有3 个峰值，能够对3 个亮点进行识别。图7 是θ=90° 时的方位谱，此时鱼雷位于潜艇的正横方向，方位谱函数有3 个峰值，识别效果最好。这里只给出了θ ∈［0，90°］时典型角度的方位谱，当θ ∈(90°，180°］时，情况相似。

图6 θ=20° 时方位谱Fig.6 The azimuth spectrum of θ=20°

图7 θ=90° 时方位谱Fig.7 The azimuth spectrum of θ=90°

本文只给出θ 取几个典型值时的方位谱，在具体仿真中，θ 的取值间隔可以无限小。由仿真可以得出，当照射角θ∈［10°，170°］时，可以区分2 个亮点，能够对潜艇尺度进行识别;当照射角θ ∈［20°，160°］时，可以区分3 个亮点，对潜艇目标的识别达到很好的效果;而在潜艇舰首和舰尾区即θ ∈［0°，10°)和θ ∈(170°，0°］时，不能对潜艇进行尺度识别。

4 结 语

在本文提出的潜艇目标尺度识别方法中，在建立混响条件下潜艇目标亮点模型的基础上，用自身多普勒抑制技术对带有混响的回波进行混响抑制，然后采用MUSIC 算法，对潜艇目标亮点的方位进行精确估计。仿真结果表明，该方法能够很好地实现混响干扰下对潜艇目标的尺度识别，具有很高的理论价值和现实意义。

［1］刘伯胜，雷家煜.水声学原理［M］.哈尔滨:哈尔滨工程大学出版社，1993.

［2］苏绍璟，郭熙业，王跃科.一种海底混响时间序列仿真方法研究［J］.系统仿真学报，2010，88(8):1853-1861.

SU Shao-jing，GUO Xi-ye，WANG Yue-ke.A bottom reverberation time sequence simulation method research［J］.Journal of System Simulation，2010，88(8):1853-1861.

［3］陈文剑，孙辉，朱建军，等.基于分数阶傅里叶变换混响抑制的目标回波检测方法［J］.声学学报，2009.34(5):408-415.

［4］董阳泽，刘平香.声自导鱼雷反水声对抗仿真研究［J］.系统仿真学报，2008，20(3):767-776.

［5］蔡平，梁国龙，葛凤翔，等.界面混响信号的仿真研究［J］.哈尔滨工程大学学报，2000，21(4):31-35.

［6］汤渭霖.声呐目标回波的亮点模型［J］.声学学报，1994，9(2):92-100.

TANG Wei-lin.Sonar target echo highlight model［J］.Chinese Journal of Acoustics，1994，19(2):92-100.

［7］徐瑜，苑秉成，唐波.基于亮点模型的潜艇目标回声过渡特性分析［J］.鱼雷技术，2012，20(2):153-156.

［8］王明洲，黄晓文，郝重阳.基于声学亮点特征的水下目标回波模型［J］.系统仿真学报，2003，15(1):21-25.

［9］何心怡，蒋兴舟.浅海混响与鱼雷抗混响［J］.鱼雷技术，2001，9(4):13-16.

HE Xin-yi，JIANG Xing-zhou.Reverberation in shallow sea and anti-reverberation for torpedo［J］.Torpedo Technology，2001，9(4):13-16.

［10］刘朝晖，马国强.水下声自导武器目标识别技术综述［J］.声学与电子工程，2004，75(3):25-30.

LIU Chao-hui，MA Guo-qiang.Underwater homing weapon target identification technology［J］.Acoustics and Electronics Engineering，2004，75(3):25-30.

［11］徐枫，严冰，王海陆，等.鱼雷垂直目标亮点高分辨算法仿真与试验研究［J］.鱼雷技术，2009，17(6):35-40.

XU Feng，YAN Bing，WANG Hai-lu，et al.Torpedo vertical highlights high resolution algorithm simulation and test research［J］.Torpedo Technology，2009，17(6):35-40.