基于块体单元法的白鹤滩左岸边坡稳定性分析
2014-12-04郑惠峰吴关叶徐建荣
郑惠峰,吴关叶,徐建荣
(中国电建集团 华东勘测设计研究院有限公司,杭州 310014)
1 工程地质条件
白鹤滩水电站位于金沙江下游四川省宁南县和云南省巧家县境内,上游与乌东德水电站相接,下游与溪洛渡水电站相连。电站初拟装机容量14 000 MW,是西电东送骨干电源点之一。电站枢纽由拦河坝、泄洪消能设施、引水发电系统等主要建筑物组成。拦河坝为混凝土双曲拱坝,坝顶高程834 m,最大坝高289 m。泄洪设施由坝身6个表孔及7个深孔和左岸3条无压直泄洪隧洞组成,坝下设水垫塘、二道坝。地下厂房采用首部开发方式布置,左右岸各布置8台百万千瓦机组。
白鹤滩水电站坝址左岸谷肩以上总体表现为斜坡地形,谷肩以下为陡壁与缓坡相间地形,陡壁间有较窄的缓坡台地相连,缓坡台地顺岩流层面发育,其上堆积有上级陡壁岩体的崩积物(图1)。左岸谷肩以下综合地形坡度42°左右。左岸谷肩以下自然边坡高度200~440 m。金沙江由南向北流经坝址区。
左岸边坡主要为二叠系上统峨眉山组玄武岩(P2β),为第2至第4岩流层(P2β2至 P2β4),为单斜构造,岩流层产状 N40°~50°E,SE∠15°~20°,倾向上游偏右岸,岩层走向与河流流向约呈45°斜交,属于斜顺向坡。
左岸边坡断裂构造发育,主要发育2组N W向(N30°W,N60°W)陡倾角断层,其中规模较大并对岸坡发展有一定控制作用的断层有F13,f114,F14,F16(N60°W),F33,f108(N30°W)等。NE向断层规模较大的为F17断层,自上游谷肩部位,斜切左坝肩抗力体边坡的中部,延伸至勘Ⅹ线的坡底(河中),将左岸上游部分坡体一分为二。
层间错动带C3-1,C3发育于左岸坡的中上部,形成宽50~70 m的斜坡地形,对左岸上部边坡的发展形成一定的控制作用。其上盘P2β4层坡体内,层内错动带较发育,但大多规模小,性状不稳定,连续性差,一般仅对局部边坡起影响作用。层间错动带C3-1下盘层坡体内,层内错动带不发育,坡面多为陡壁地形;其下层柱状节理玄武岩层内错动带发育,且与岩流层小角度相交,其中规模最大的为LS337,由于其性状差,分布范围广,局部范围倾角大(30°),对左岸边坡稳定起重要的控制作用。
左岸边坡卸荷裂隙主要表现为拉裂缝,宽度大于10 c m的卸荷裂隙有15条。边坡长大卸荷裂隙走向以NS向为主,与河流流向基本平行,且主要分布于勘Ⅰ线至勘Ⅹ1线720 m高程以上,断层F14下游和LS337上盘范围内岸坡。其中以J110规模最大,宽5~30 c m,延伸长度165 m,距坡面最大水平距离为106 m,由数条雁行式排列的拉裂缝连接而成。

图1 白鹤滩左岸边坡地质平面图Fig.1 Geological plan of the left bank slope of Baihetan
2 左岸边坡变形特征及变形机理
左岸边坡岩体变形主要表现为岩体中产生卸荷裂隙和边坡表层岩体的整体松弛。具有以下几个方面的特征:①左岸坎状地形平缓地带均沿缓倾错动带形成,反映了岸坡改造过程中错动带的底滑面作用,缓倾角错动带是边坡稳定的控制性因素;②在铅直方向上,卸荷裂隙大部分止于缓倾角错动带。C3-1,LS337均限制了卸荷裂隙的向下发展。说明缓倾角错动带是边坡岩体变形的控制性结构面;③大型陡崖均呈NW向,沿NW向断层发育,表明规模较大的N W向断层是边坡变形的侧向控制边界,断层下游侧一定范围岩体的变形发展速率要明显大于断层的上游侧。如NW向断层F14的上下游侧岩体风化与卸荷强度差异明显,上游侧卸荷深度明显小于下游侧;④同一缓倾角错动带上盘的卸荷裂隙,在一定范围内表现出水平发育深度下游大于上游的特点,C3-1上盘和LS337上盘长大卸荷裂隙发育均有此特点,表明变形有从下游向上游渐进式发展的特点。这种渐进式发展会受到NW向断层如F14的局部控制。
由左岸边坡变形特征分析可以认为缓倾角错动带和N W向断层是左岸边坡变形的主要控制因素。边坡变形机理如下:随着河谷的下切,边坡岩体产生向临空方向的卸荷变形,包括地应力释放而产生的岩石回弹变形、结构面的张开变形和沿错动带的剪切变形等;边坡形成后,由于应力释放,首先在边坡前缘坡顶形成应力松弛区或拉应力区,从而形成卸荷裂隙(即拉裂缝);当缓倾角错动带在坡脚出露时,沿错动带产生剪切变形,剪切变形会弱化错动带的工程地质性状,其上盘岩体由于应力松弛而出现裂隙张开,该变形破坏机制是比较典型的“蠕滑拉裂”型;随着时间的推移,卸荷裂隙逐渐连通并与NW向结构面组合形成可动块体,沿缓倾角错动带产生滑动破坏或解体破坏;对于缓倾角错动带来说,越靠近临空面(前缘),剪切变形越大,卸荷、风化、地下水作用越强烈,错动带的工程地质性状也越差。所以破坏往往是从前缘开始,向后缘发展。由于岩层产状倾向上游偏右岸,缓倾角错动带临空是由下游开始,向上游发展,故边坡变形自下游向上游渐进式发展。NW向结构面尤其是规模较大的断层,对左岸边坡由下游向上游发展的变形也起到一定的限制作用,即NW向结构面下游侧岩体变形明显大于上游侧,规模较大的NW向断层如F14,F12,F13等都是边坡变形的侧缘控制边界。
综上所述,坝区与左岸边坡走向近平行的断层不发育,规模较小,且倾角近直立,不会在边坡面上临空出露,因此不会产生沿陡倾角结构面的平面滑动破坏;坝区缓倾角结构面与边坡走向斜交,因此也不会产生沿缓倾角结构面的平面型滑动。以缓倾角层间层内错动带作为底滑面,NW向断层为侧滑面,NN W向断层及顺河向长大裂隙为后缘面的结构面组合块体滑动破坏为左岸边坡主要的失稳模式。
3 岩石边坡稳定分析的块体单元法
3.1 边坡稳定分析方法的一般认识
在岩体力学分析方法中,能否合理反映结构面的影响,成为衡量该方法是否适用于岩体变形和稳定性分析的重要标准。从最初的刚体极限平衡法[1],到基于连续介质力学的有限单元法[2-4]等,以及基于非连续介质力学离散单元法[5]、DDA方法[6]、刚体-弹簧元法[7]、块体单元法[8-10]等,直至介于二者之间的数值流行方法[11],计算岩体力学中各种分析方法提出的初衷和发展的方向均以模拟岩体二元结构下的不连续变形和稳定问题。
针对白鹤滩左岸边坡块体系统稳定性分析,传统的刚体极限平衡法主要的局限在于如何准确地描述复杂的结构面。连续介质力学方法同时存在复杂地形面、大量结构面的建模问题和岩石块体间不连续变形的适应性问题。因此采用不连续岩体力学方法更为合适,其中三维弹黏塑性块体单元法(BEM)具有独特的优势。
3.2 块体单元法基本原理
块体单元法以块体系统自动识别方法[12]作为前处理器。只需要给出结构面的产状和出露位置即可自动生成计算区域内的块体系统,其应用于岩石边坡等被大量结构面切割的复杂岩体结构的信息自动识别,能大为降低前处理工程量和准确性。
块体单元法首先假定块体之间是面-面接触,同时常规的弹黏塑性块体单元法还假定岩石块体为刚体,只考虑结构面的变形和强度特性。岩体结构块体系统位移与稳定分析的基本方程由块体系统的平衡方程、结构面变形与块体位移的几何相容方程、以及结构面上的弹黏塑性本构方程构成。
块体单元法对块体或块体组合安全系数的评价可采用2种方式:一种通过降低块体组合相关结构面强度参数(f,c)推求块体组合的强度储备安全系数;另一种将块体单元法计算所得的块体的应力结果应用于刚体极限平衡法,直接用力的平衡条件计算块体组合的安全系数。本文中的块体安全系数是通过第一种方式计算得到。
4 白鹤滩左岸边坡块体系统稳定分析
4.1 左岸边坡三维块体系统建立
运用块体系统识别方法,将左岸边坡大多数结构面(层间层内错动带、断层、裂隙等)纳入考虑后,成功地进行了白鹤滩坝区左岸边坡块体切割,建立了左岸边坡块体系统模型(图2)。块体系统模型共包含结构面74条,共形成546个块体单元。其中,规模较大的主要可动块体基本特征见表1。

图2 左岸块体系统局部分解Fig.2 Partial decomposition of block system of the left bank slope

表1 左岸边坡主要可动块体基本特征Table 1 Basic characteristics of movable blocks of the left bank slope
4.2 左岸边坡块体稳定性分析
在建立左岸三维块体系统模型基础上,采用弹黏塑性块体单元法(BEM)计算边坡块体或块体组合强度储备稳定安全系数。表2为稳定性计算中主要结构面参数物理力学参数。
采用常规的三维刚体极限平衡法进行块体稳定性计算,计算成果见表3。从左岸强卸荷边坡主要块体持久工况下稳定安全系数对比可以看出,2种方法计算成果基本一致。同时块体单元法分析表明,在对左岸块体系统进行整体分析的情况下,与深部卸荷裂隙J110和缓倾角层内错动带LS337相关的1-1#块体稳定安全系数最小,且1-1#块体位于边坡前缘,因此,可以认为,1-1#块体为左岸边坡的控制性块体(或关键块体),是边坡加固的重点部位。
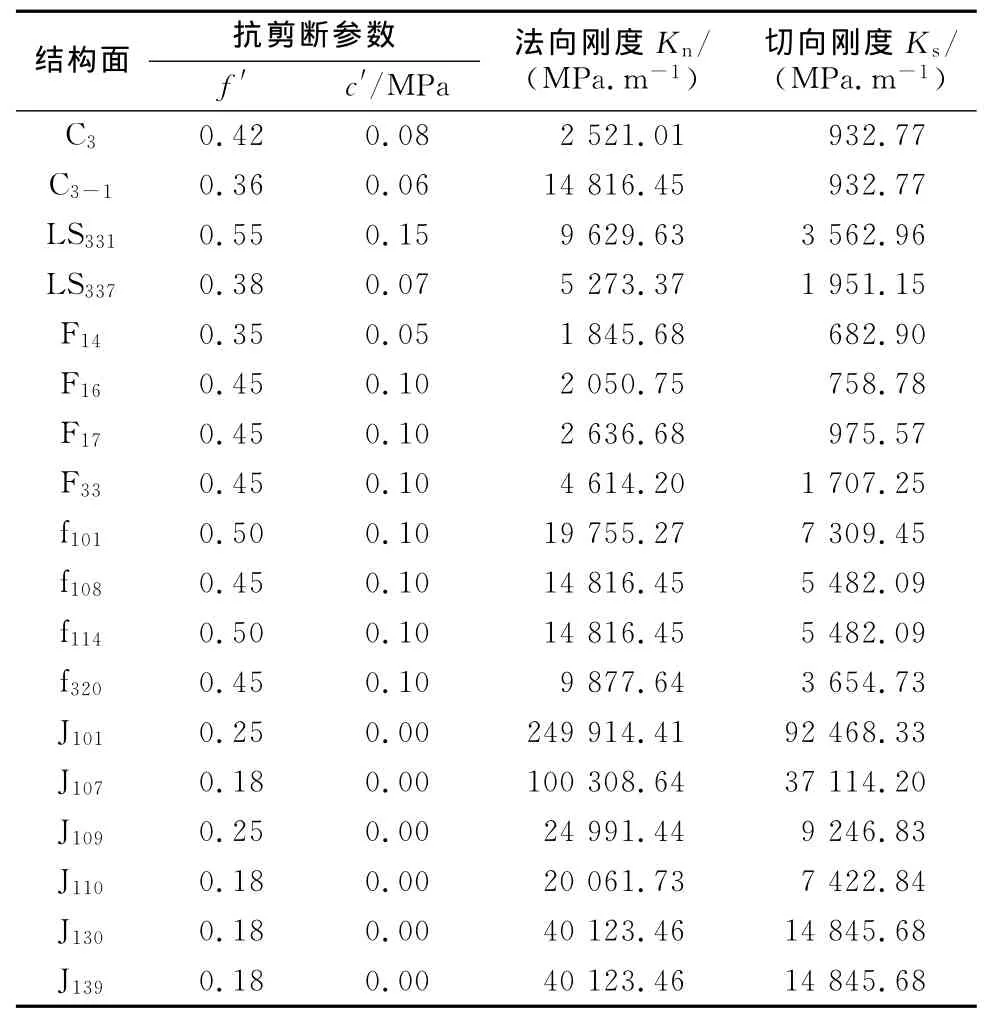
表2 主要结构面物理力学参数Table 2 Physical and mechanical properties of discontinuities

表3 左岸边坡主要特定块体稳定性分析成果Table 3 Results of stability analysis for movable blocks of the left bank slope
4.3 地质力学模型试验验证
为进一步研究白鹤滩左岸边坡稳定安全度,采用二维地质力学模型试验方法,进行边坡块体稳定性评价。试验模型主要模拟 LS337,C3-1,J110,J136,f101,J108等结构面,试验中主要对缓倾角错动带LS337,C3-1进行降强,然后再对块体系统进行适当超载,以研究边坡的破坏过程、破坏形态和破坏机理的同时,提出边坡的稳定安全系数。
模式试验表明,1-1#块体安全系数为1.059,2#块体稳定安全系数为1.078。地质力学模型试验成果与块体单元法(BEM)计算结论基本一致。
图3为模型最终的破坏形态。
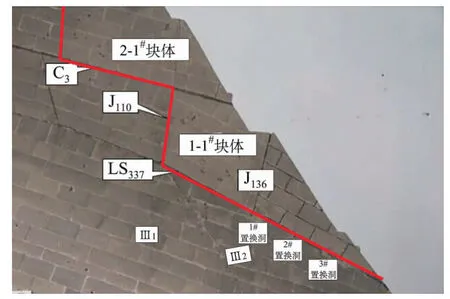
图3 左岸边坡模型最终破坏的形态Fig.3 Final f ailure mode of the left bank slope model
5 结 论
本文分析了白鹤滩水电站左岸强卸荷发育边坡基本地形地质条件、边坡变形特征及变形机理。以缓倾角层间层内错动带作为底滑面,NW向断层为侧滑面,NN W向断层及顺河向长大裂隙为后缘面的结构面组合块体滑动破坏为边坡主要失稳模式。
采用块体单元法(BEM)进行白鹤滩左岸边坡块体系统稳定性分析,计算了各特定块体各工况下强度储备安全系数。分析表明:
(1)1-1#块体天然条件下稳定安全系数略大于1.0,处于基本稳定状态,2#块体稳定性安全系数也较低。因此,1-1#和2#块体均需进行加固处理。
(2)左岸特定块体安全系数对比可以看出,以层内错动带LS337为底滑面的1-1#,2#,3#块体稳定安全系数明显小于其他块体,可以认为LS337对左岸边坡块体稳定的控制性作用。
(3)由1-1#,2#,3#块体间实际存在的空间关系可以看出,2#,3#块体位于1-1#块体后缘,尚不具备临空条件,只有在1-1#块体已经滑动失稳的条件下,2#块体和3#块体前缘才处于临空状态,具备滑动失稳的条件。从3个块体的稳定安全系数来看,处于前缘的1-1#块体安全系数最小,因此,可以认为1-1#块体为左岸边坡的关键块体,是左岸边坡加固处理的重点区域。
块体单元法(BEM)稳定安全系数计算成果与常规刚体极限平衡法及地质力学模式试验成果基本一致。同时地质力学模型试验也表明处于边坡前缘的1-1#块体为左岸块体系统边坡的关键块体。
[1]陈祖煜,弥宏亮,汪小刚.边坡稳定三维分析的极限平衡法 [J].岩 土 工 程 学 报,2001,23(5):525-529.(CHEN Zu-yu,MI Hong-liang,WANG Xiao-gang.A Three-di mensional Li mit Equilibriu m Method f or Slope Stability Analysis[J].Chinese Jour nal of Geotechnical Engineering,2001,23(5):525-529.(in Chinese))
[2]BENKO B.Numerical Modeling of Complex Slope Defor mations[R].Saskatoon,Canada:Depart ment of Geological Sciences,University of Saskatachewan,1997:366-372.
[3]EBERHARDT E,STEAD D,COGGAN J,et al.An Integrated Numerical Analysis Approach to the Randa Rock Slide[C]//Proceedings of the 1st European Conference on Landslides.Prague,Czech Republic,June 24-26,2002:355-362.
[4]DA WSON E M,ROT H W H,DRESCHER A.Slope Stability Analysis by Strength Reduction[J].Geotechnique,1999,49(6):835-840.
[5]PRIEST S D,SA MANIEGO J A.A Model for the A-nalysis of Discontinuity Characteristics in Two Di mensions[C]//Proceedings of the 5th ISRM Congress.Melbourne,April 10-15,1983:199-207.
[6]吴建宏,大四有三,石根华,等.三维非连续变形分析理论及其在岩石边坡数值仿真中的应用[J].岩石力学与工程 学 报,2003,22(6):937-942.(WU Jian-hong,OHNISHI Y,SHI Gen-hua.Three-dimensional Discontinuous Defor mation Analysis and Its Application to the Rock Slope Toppling[J].Chinese Journal of Geotechnical Engineering,2003,22(6):937-942.(in Chinese))
[7]KAWAI T.A New Discrete Model for Analysis of Solid Mechanics Problem[J].Science Kenkyn,1977,29(4):208-210.
[8]CHEN S H.A New Develop ment in Elastic-viscoplastic Block Theor y of Rock Masses[C]//Pr oceedings of the Eighth Inter national Conference on Co mputer Methods and Advances in Geo mechanics,West Virginia(USA)A.A.Balkema,May 22-28,1994:2235-2240.
[9]陈胜宏.岩体的广义弹粘塑性块体理论[J].水利学报,1996,(1):78-84.(CHEN Sheng-hong.A General For mulation of Elasticvisco-plastic Block Theor y of Rock Masses[J].Journal of Hydraulic Engineering,1996,(1):78-84.(in Chinese))
[10]郑惠峰,汪卫明,陈胜宏.弹粘塑性块体单元法在龙滩水电站右坝肩边坡稳定分析中的应用[J].岩土力学,2006,27(1):107-112.(ZHENG Hui-feng,WANG Wei-ming,CHEN Sheng-hong.Application of Elasto-viscoplastic Block Element Method to Stability Analysis of Right Abutment Slope in Longtan Hydropower Project[J].Rock and Soil Mechanics,2006,27(1):107-112.(in Chinese))
[11]石根华.数值流行方法与非连续变形分析[M].裴觉民,译,北京:清华大学出版社,1997.(SHI Gen-hua.Nu merical Manifold Method and Discontinuous Defor mation Analysis[M].Translated by PEI Jue-min.Beijing:Tsinghua University Press,1997.(in Chinese))
[12]汪卫明,陈胜宏.三维岩石块体系统的自动识别方法[J].武汉水利电力大学学报,1998,31(5):51-55.(WANG Wei-ming,CHEN Sheng-hong.Auto matic I-dentification Met hod for Three di mensional Rock Block Systems[J].Journal of Wuhan University of Hydraulic and Electric Engineering,1998,31(5):51-55.(in Chinese))
