基于瞬态动力学的主汽阀关闭强度研究
2014-12-03韩方亮胡少文
韩方亮,孙 轶,胡少文
(长动集团 武汉汽轮发电机有限公司汽轮机研究所,武汉 430074)
汽轮机主汽阀是主蒸汽进入汽轮机的总阀门,对保证汽轮机启停和运行起关键作用,其通常为一个二位阀,即只有全开和全关两种状态。在危急情况下,主汽阀要能在极短的时间内快速关闭,切断汽源,使机组迅速停机,以防止机组超速过大,从而避免事故发生。
从汽轮机的安全角度来说,主汽阀的关闭速度越快越好,这样可以最大限度避免汽轮机发生超速,但阀门关闭速度过快,阀碟和阀座之间会发生猛烈的碰撞,严重时将导致阀碟和阀座碎裂,甚至会发生汽轮机飞车事故。因此,设定合适的关闭速度,详细校核阀门关闭时的冲击强度,是设计中必须考虑的关键问题。
主汽阀关闭时,运动件以一定的速度撞向阀座,同时受到主汽阀操纵座弹簧力、蒸汽压力等多种外力的作用,因此,我们不能简单地按照静力学的方法计算所承受的力,而应该依据冲击载荷理论进行校核。我们知道,传统的理论计算方法基于多种假设和经验公式,有一定的局限性。随着有限元技术的不断发展和完善,尤其是瞬态动力学仿真技术的成熟,对于这种短时冲击载荷的计算已经很方便。本文采用有限元瞬态动力学方法,对一种侧向布置的主汽阀进行了仿真计算,能为设计人员提供设计指导。
1 部套结构和分析模型
图1为武汉汽轮发电机有限公司某型侧向布置的主汽阀和主汽阀的操纵座装配总图,该主汽阀布置在汽缸左侧,直接与汽缸蒸汽室连接,操纵座布置在主汽阀下部。

图1 部套结构简图(旋转后)
模型圆周对称,只取1/8进行仿真分析。弹簧采取刚度等效的原则进行简化,预压长度与设计值一致。网格划分局部视图如图2所示,在接触碰撞区域加密了网格。为方便后文描述,部件2、3、5、6、7、9合称为运动件。仿真的开始点为下文所述t1时刻,即阀门处于碰撞初始点,以速度V1撞向阀座。这样做是为了减少计算量和时间,当然,也可从阀门全开状态的t0时刻开始计算,但这个过程只是简单的刚体加速过程,计算时间长,没有必要。
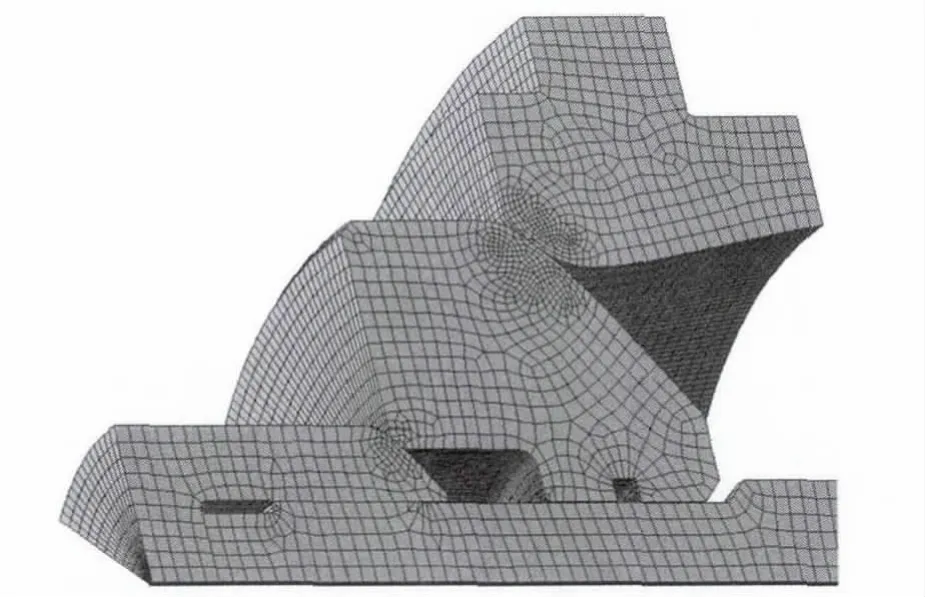
图2 1/8有限元模型及网格(旋转后)
2 理论分析
2.1 主汽阀关闭速度的讨论
t0时刻,阀门处于全开状态,油动机提升力处于开始减小的初始点。阀门运动件在向下拉的弹簧力T0、重力G、逐渐减小的油动机提升力的综合作用下开始向下变加速运动,其中弹簧力和油动机提升力都是时间的函数。t1时刻,阀碟关闭的瞬间,阀门运动件以速度V1与阀座发生碰撞。t1时刻后,碰撞冲击波在构建中震荡,并衰减直到稳定,这个时间极短。通过油动机设计特性我们知道,在阀门碰撞前,油动机会给阀门运动件一个缓冲力,使实际阀门关闭时间和速度发生了偏移,如图3所示。通过主汽阀操纵座和油动机的设计参数,可以估算阀门关闭tc≈0.2s,t1≈0.35s。
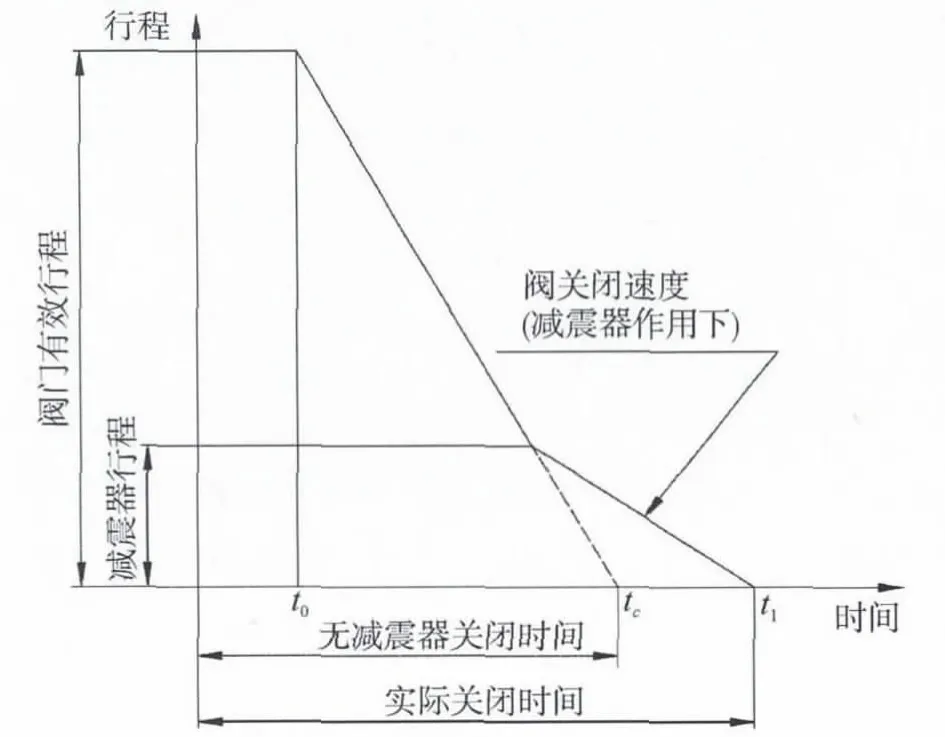
图3 阀关闭时间和速度关系图
文献[1]提出阀门关闭时速度的近似计算公式:

其中:H为阀碟开启行程100mm;t取值范围为0.2~0.35s。
综上所述,阀门运动件关闭时具有的碰撞速度V1=0.286~0.5m/s。本文取最大碰撞速度0.5m/s进行仿真计算,作为设计校核依据。
2.2 t1时刻阀门的受力分析
从以上分析可知,t1时刻,阀门运动件以速度V1与阀座发生碰撞,同时承受弹簧力T1、运动件重力G,由于此时阀门处于关闭状态,主汽阀上下腔室不连通,阀碟和预启阀还承受上部主蒸汽压力P,其中:
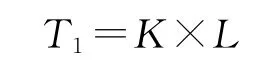
式中:K为弹簧刚度;L为预压长度。
2.3 瞬态动力学分析基础
动力学通用运动方程[2]为:

式中:[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵。
对于瞬态动力学分析,方程保持上述形式。阻尼是动力学分析的一大特点,也是一个易于引起困惑的地方,它只影响动力响应的衰减,而本文关心的是响应的极值,所以在分析时忽略了阻尼,则运动学方程简化为:

求解瞬态动力学方程有两种方法:模态叠加法和直接积分法。模态叠加法计算过程是:确定结构的固有频率,乘以正则化坐标,然后加起来计算位节点的位移解,这适用于振型n1≤n的情况。直接积分法直接用来求解运动方程,适合有效振型较多的情况,占用很大的计算资源。瞬态分析运动方程保持为时间的函数,可以通过显式或隐式方法进行求解,除了Δt要求很小的情况,隐式积分法对于大多数问题都是有效的。综合考虑求解精度和效率,本文选取隐式求解器模态叠加法进行求解。
2.4 接触形式讨论
预启阀与阀碟,阀碟与阀座碰撞不能简单地处理成线性的无摩擦接触。在构件高速碰撞的过程中,接触面不仅存在法向力的传递,还存在切向的单元滑移和变形,所以采用摩擦接触条件更接近实际情况。摩擦接触是一个多次迭代,允许法向分离和切向滑移的复杂状态变化非线性过程,系统的刚度依赖于接触状态。实际接触体是互相不穿透的,因此必须加一个强制接触协调法则,防止互相穿透。常用的接触协调方法有Pure Penalty法和Augmented Lagrange法,这两种方法都基于罚函数方程[2]:

由上式得出,接触力一定时,接触刚度越大,穿透量越小,计算依赖接触刚度的取值。而Augmented Lagrange法增加了额外因子λ,方程变为:
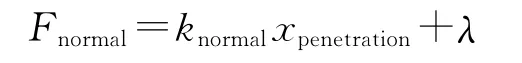
由于λ因子的加入,对于罚刚度的值变得不敏感,增加了求解的稳定性和收敛性。依据文献[3]选取摩擦系数0.13,强制接触协调法则采用Augmented Lagrange法,接触刚度随迭代次数更新。
3 计算结果和分析
3.1 计算结果
阀门关闭时的碰撞过程极短,计算初始条件取V1=0.5m/s,时间历程2ms。由于计算过程没有考虑阻尼和能量的溃散,结果呈现一个正弦分布状态,分析只截取一个周期。
如图4 所示,阀门在关闭过程中,阀碟与阀座、预启阀与阀碟的最大应力都发生在碰撞接触面,其它区域应力很小。图5、图6、图7反映了在0.5ms内阀座、阀碟、预启阀接触面应力随时间的变化趋势。图8反映了碰撞过程中弹簧的长度变化。

图4 应力分布图
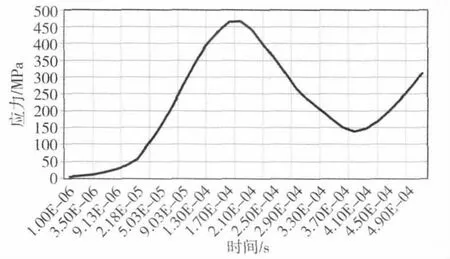
图5 阀座接触面应力分布

图6 阀碟接触面应力分布

图7 预启阀接触面应力分布
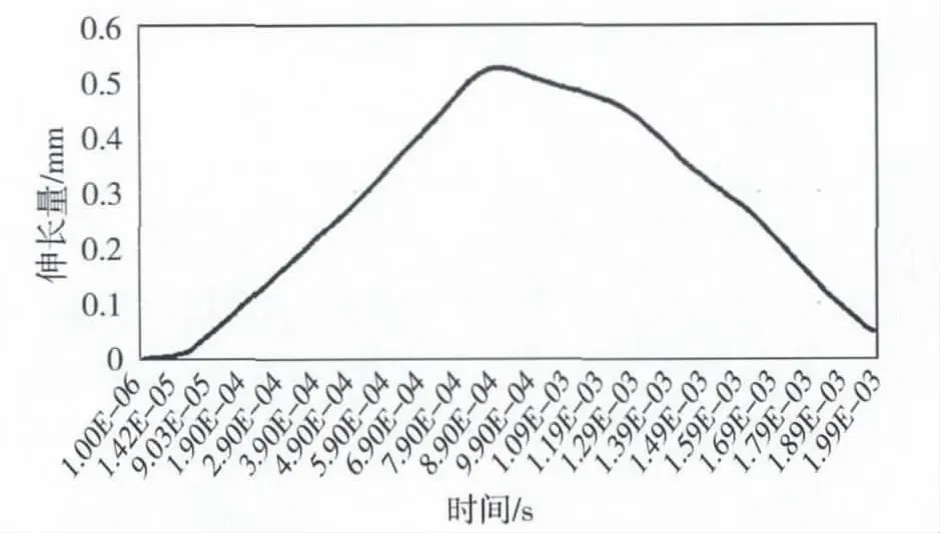
图8 2ms时间内弹簧变形量
3.2 结果分析
图5、图6显示,在0.19ms时,阀座接触面应力为467.72 MPa,对应的阀碟接触面应力为499.69MPa,达到最大值。图6和图7显示,阀碟和预启阀接触面的应力分布比阀碟与阀座应力分布滞后,因为预启阀和阀碟都是运动件,只有当阀碟与阀座发生碰撞限位后,预启阀和阀碟才会发生相对运动并碰撞,这个过程会滞后。在0.25ms时,预启阀接触面应力为304.19MPa,对应的阀碟接触面应力为306.13MPa,达到最大值。应力最大时刻即碰撞速度由V1减小到零、动能转变成构件的变形能的时刻。此后,反弹发生,冲击波在构件内部传递和震荡,应力分布呈现一个正弦分布。
图8反映了2ms内弹簧的伸长量,弹簧变形为零即弹簧为预压长度,此时阀门完全呈关闭状态。从图中可以看出,在碰撞反弹过程中,弹簧伸长量呈正弦分布,始终为正值,即阀门始终是关闭状态,不会因关闭不严而漏汽。
设计时,阀门发生碰撞的区域会焊接司太立合金以增加强度,其σ0.2=515MPa。表1 显示,阀碟与阀座碰撞接触面安全系数偏小,需要对设计进行优化,减小阀碟关闭时的应力。
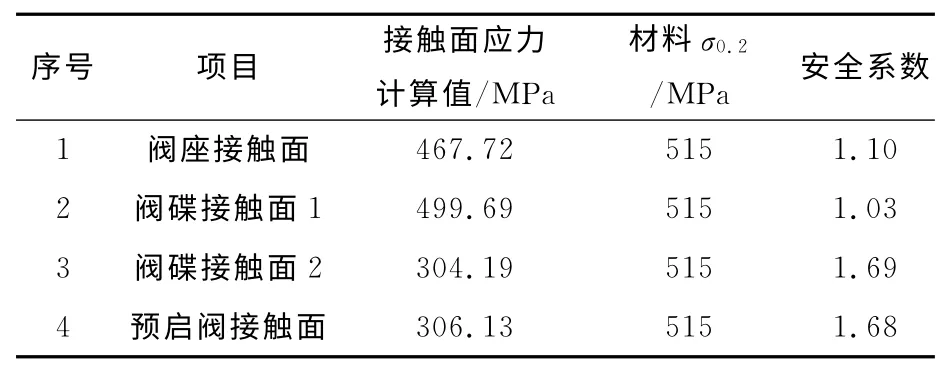
表1 接触面强度校核表
4 优化设计
4.1 优化方案
通过理论分析,阀门关闭时,阀碟与阀座接触面应力值偏大是因为运动件动能都被阀碟和阀座吸收[4],针对这种情况,可以在阀碟上开一个弹性卸载槽来分担部分冲击能量。优化方案见图9。
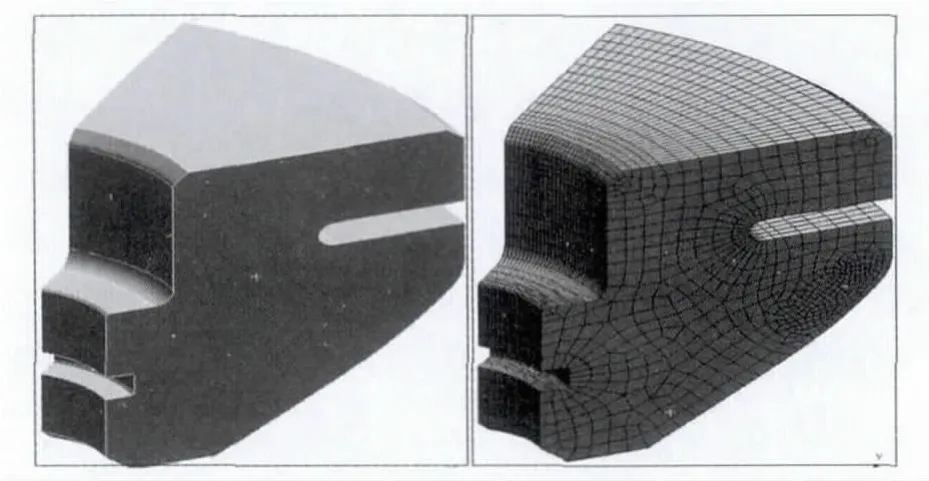
图9 阀碟优化方案
4.2 计算结果和讨论
其它边界条件不变,对阀碟优化设计后的模型进行计算,结果如图10、图11所示。在阀碟上增加卸载槽后,阀座接触面最大应力由467.72 MPa减小到429MPa,对应阀碟接触面最大应力由499.69MPa减小到461.84MPa。在整个冲击能量转化成构建变形能的过程中,阀座和阀碟的应力均不同程度减小,证明设计上采用增加卸载槽的方案是有明显效果的。

图10 阀座接触面应力分布
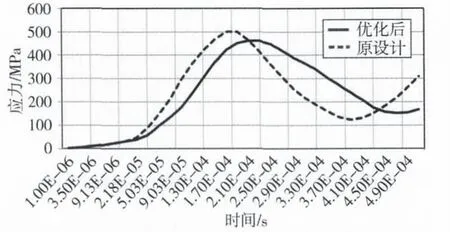
图11 阀碟接触面应力分布
5 结论
本文将瞬态动力学方法应用到汽轮机主汽阀关闭强度研究中,对瞬态动力学分析的几个主要问题进行了讨论,提出了关键步骤的选择方案,可供业内相关人员参考和借鉴。本文针对一个实际产品进行了强度分析,发现原有设计方案的阀碟和阀座接触区域的安全系数偏小。依据分析结果,本文提出了一种结构优化方案,用来指导设计工作。
阀门关闭动强度的研究将是阀门设计的一个重要研究方向。希望本文能为瞬态动力学研究方法在阀门优化设计中的工程应用起到积极的推进作用。
[1]丁有宇.汽轮机强度计算[M].北京:水利电力出版社,1985.
[2]蒲广益.ANSYS Workbench 12基础教程与实例详解[M].北京:水利水电出版社,2010.
[3]姜求志,王金瑞.火力发电厂金属材料手册[M].北京:中国电力出版社,2001:720-847.
[4]蒋浦宁.汽轮机主汽阀关闭动强度分析和研究[J].热力透平,2008,37(4):243-248.
