基于结构可靠性的涡轮叶片三维气动设计优化
2014-12-03彭茂林孙吉宏
彭茂林,刘 波,孙吉宏
(海军装备技术研究所,青岛266012)
在将高温高速燃气的热力学能转换为涡轮机械能的过程中,涡轮叶片起到至关重要的作用。能量转换的效率与叶片的形状密切相关[1],气动效率最大化一直是研究者努力追求的目标[2-4],但是气动效率提高的同时往往会牺牲其它优良性能,比如强度。因此,在对涡轮叶片进行气动设计优化的同时,如何保证叶片的强度,满足可靠性要求,已成为难点重点问题。作者在文献[5]中详细介绍了涡轮叶片的参数化建模方法,在文献[6]和文献[7]中进一步研究了涡轮叶片气动效率的计算方法和结构可靠度计算方法,在文献[8-9]中研究了基于响应面法的可靠性稳健设计优化方法,在这些工作的基础上,本文将叶片的结构系统可靠度作为基本约束条件,对某船用涡轮叶片进行了三维气动设计优化,在提高效率的同时,保证了叶片的结构可靠性,取得了较好的效果。
1 基于结构可靠性的涡轮叶片气动设计优化模型
涡轮叶片气动设计优化模型见下式:
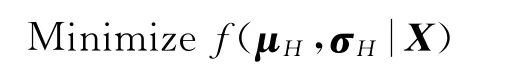
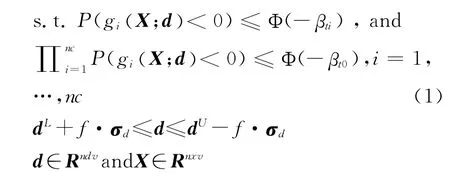
式中:f(μH,σH|X)为涡轮叶片设计优化的代价函数,μH,σH分别为结构多性能目标函数的均值、标准方差向量,X为结构的nxv维随机变量向量;d为设计变量向量;dL,dU,σd分别为设计变量d的许可上、下限以及标准方差向量;gi(X;d)为结构的第i个极限状态函数;nc,nxv,ndv和βti分别为结构可靠度约束、随机变量、设计变量的个数以及第i个失效模式对应的结构可靠度指标目标值;P(gi(X;d)<0)为gi(X;d)的概率;Φ(·)为标准正态累积概率分布函数;为连乘符号;βt0为多失效模式下的结构系统可靠度指标;f为设计变量的稳健性水平,以保证设计变量的最终优化结果超出取值范围的边界的概率小于等于Φ(-f),通常取3≤f≤6。多目标可靠性稳健设计代价函数f(μH,σH|X)为各目标函数的加权和的形式,根据目标的不同特性而分为以下几类:
第1类:对于望小特性:

第2类:对于望大特性:
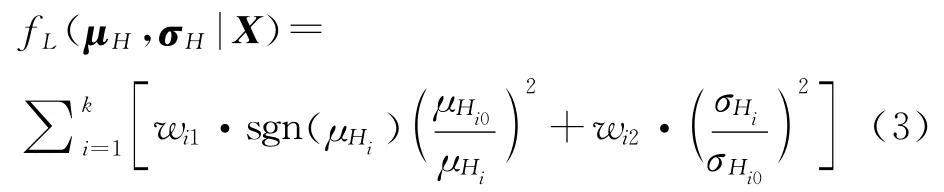
第3类:对于望目特性:

式中:hit和分别为第i个目标函数的望目特性目标函数的目标均值和初始均值。
第4类:混合型

从表达式(2)-(5)可以看出,为了解决由于各个目标函数的量纲不同的问题,代价函数的各项都通过除以其初始设计值来进行无量纲化处理。权值的大小反映了设计者对于各项性能指标的偏好程度。多目标可靠性稳健设计优化代价函数不但寻求结构性能目标均值的最优,也期望结构性能的标准方差能达到最小。而传统设计优化只追求性能目标的均值最优解,但不考虑变量的随机性。
2 涡轮叶片气动设计优化代价函数
2.1 性能目标函数的选取
1)对于静叶片的设计优化,选取静叶气动效率和静叶片质量为主要优化目标,其中,气动效率为望大特性目标函数,叶片质量为望小特性目标函数;
2)对于动叶片,由于其在高温高速气流推动下高速旋转,承受的应力应变及振动情况十分复杂,必须对其进行可靠性设计优化。因此,选取动叶片的气动效率作为望大特性目标函数,叶片质量为望小特性目标函数,结构可靠性为基本约束条件。
2.2 动叶片结构可靠性约束
静强度可靠性约束:
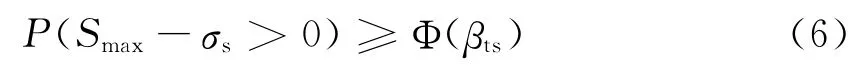
疲劳可靠性约束:

刚度可靠性约束:
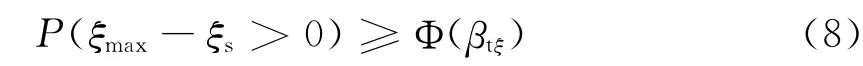
式(6)-式(8)中:Smax、εmax、ξmax分别为动叶片运行中承受的最大应力、最大应变、最大变形;σs为叶片材料工作温度下的屈服强度;ξs为叶片变形允许值;εP为涡轮设计安全寿命下概率-应力应变-疲劳寿命曲线对应的循环应变值;βts、βtP、βtξ分别为静强度、疲劳、刚度可靠度指标的目标(约束)值。
2.3 涡轮叶片气动设计优化代价函数

式中:μE、μV分别为叶片气动效率、叶片体积的均值;σE、σV分别为叶片气动效率、叶片体的标准方差;μE0、μV0分别为μE、μV在叶片初始设计参数下的取值;σE0、σV0分别为σE、σV在叶片初始设计参数下的取值。本文取w11=w12=0.9,w21=w22=0.1。
3 涡轮叶片气动设计优化方法及优化结果
3.1 优化分析方法及步骤
1)首先基于正交试验设计选取试验点并建立相应的实体及有限元模型,详细建模过程请见参考文献[5],进行热-流-固耦合有限元分析,分析流程如图1所示;
2)根据有限元分析结果得到各试验点下的叶片动能效率、最大应力应变、最大变形、体积等响应参数,采用二次多项式函数拟合各性能函数和极限状态函数对随机变量的表达式。
3)基于响应面函数,计算涡轮叶片的结构可靠度,详细分析方法参考文献[8-9]。采用多目标序列二次规划优化算法对设计参数进行寻优,得到最优设计点;
4)在最优点处再次进行热-流-固耦合有限元分析,并将分析结果加入到试验数据中,并更新响应面模型,再次计算最优设计点,如此循环迭代计算,当计算收敛到满足精度要求时,优化结果即为最优设计。
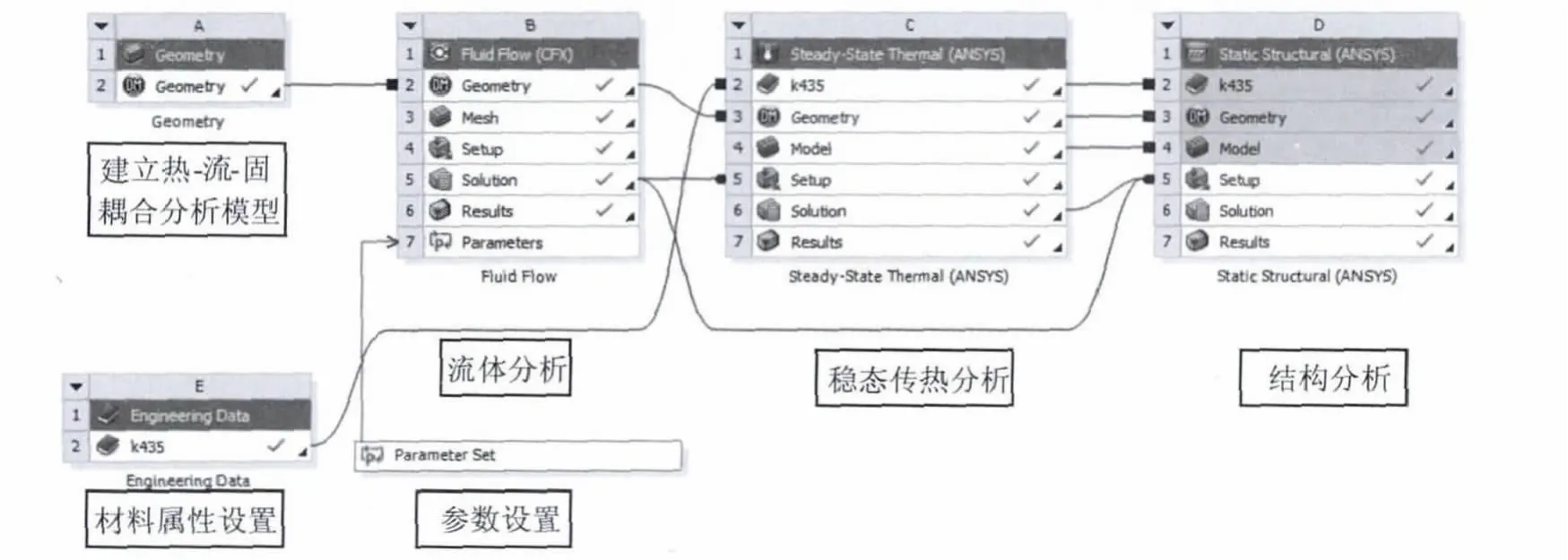
图1 涡轮叶片热-流-固耦合有限元分析流程图
3.2 优化分析结果
优化计算过程经过6次迭代,结果达到收敛要求,历时约120h。图2为气动设计优化前后流场各截面燃气压力分布对比图,从图中可以看出,优化后各截面燃气流速分布比优化前更为均匀,说明流动更平稳,流动损失就会相对减少。图3为设计优化前后50%叶高截面叶片表面湍流运动能变化对比图,湍流运动能的大小反映了流动损失的大小,从图中可以看出,经过设计优化,静动叶片的能量损失都得到明显减少,以动叶片为例,50%叶高截面表面湍流运动能最高值比优化前下降大约11.1%。图4 为设计优化前后流场及叶片模型对比图。6.61%,静、动叶片体积均值分别增加2.4%和0.64%。叶片体积增大,在制造叶片时原材料成本就会有所提高。

图2 设计优化前后流场各截面燃气压力分布对比图

图3 设计优化前后50%叶高截面叶片表面湍流运动能变化对比图

图4 设计优化前后流场及叶片模型对比图
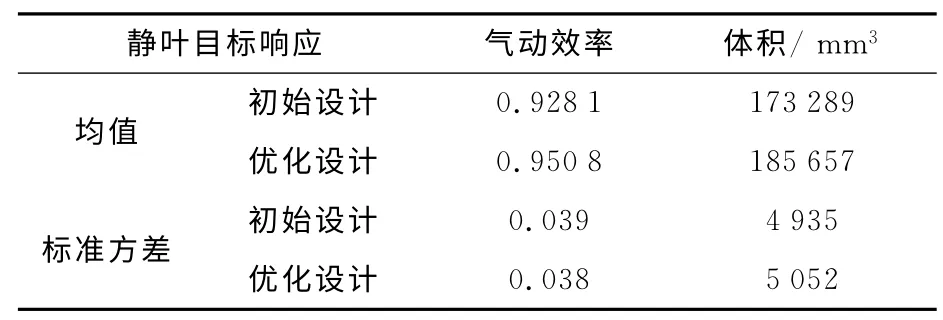
表1 涡轮静叶片性能目标设计优化结果
表1和表2分别为静、动叶片性能目标设计优化结果。从表中结果可知,经过优化后,静、动叶的气动效率均值分别提高了2.45%和6.17%,且气动效率的标准方差也有一些减小。经过设计优化,动叶片的各项结构可靠度指标都得到提高,且达到设计优化对结构可靠度的要求。优化前,动叶片的结构系统可靠度约为91.3%,而优化后动叶片的结构可靠度达到了99.87%。然而,优化后静、动叶片体积的均值和标准方差都有所增大,其中,静、动叶片体积均值分别增加7.14%和

表2 涡轮动叶片性能目标设计优化结果
4 结论
建立了涡轮叶片结构可靠性三维气动设计优化模型和代价函数,采用多学科耦合方法对叶片进行有限元分析,并给出了设计优化流程。最后,对其进行了多学科可靠性气动设计优化。结果表明,基于结构可靠性的涡轮叶片三维气动设计优化在提高叶片气动效率的同时,又可以保证叶片的结构可靠性。因此,该方法具有较高的理论及工程应用价值。但是,在保证叶片结构可靠性、提高叶片气动效率的同时,却可能要在某些性能(如叶片体积和制造成本)上付出更高的代价,因此基于结构可靠性的涡轮叶片三维气动设计优化过程也是一个权衡折中的过程。
[1]岳珠峰,李立州,王婧超.航空发动机涡轮叶片多学科设计优化[M].北京:科学出版社,2007.
[2]刘勋,周逊,温风波.F级中低热值燃料气轮机透平部分气动方案优化设计与分析[J].中国电机工程学报,2011,31(26):1-8.
[3]马洪波,朱剑,席平.基于参数化的涡轮叶片三维气动优化仿真[J].计算机仿真,2008,25(10):27-30.
[4]虞跨海,岳珠峰,杨茜.涡轮冷却叶片气动与传热设计优化[J].计算力学学报,2010,27(4):310-314.
[5]彭茂林,杨自春,曹跃云,等.基于贝赛尔曲线和粒子群算法的涡轮叶片型线参数化建模[J].中国电机工程学报,2012,32(35):101-108.
[6]彭茂林,杨自春,曹跃云.涡轮叶片三维气动分析方法研究[J].热力透平,2012,41(4):245-250.
[7]彭茂林,杨自春,曹跃云.涡轮盘片的结构可靠度计算及灵敏度分析[J].热力透平,2011,40(3):192-198.
[8]彭茂林,杨自春,曹跃云,等.涡轮叶片低周疲劳可靠性稳健设计优化研究[J].中国电机工程学报,2013,33(11):104-111.
[9]彭茂林,杨自春,曹跃云.基于响应面法的可靠性稳健设计优化方法研究[J].航空动力学报,2013,28(8):1784-1790.
