基于弹复性的第四方物流多周期网络设计

李 锐，黄 敏+，张瑞友，王兴伟

（1.东北大学 信息科学与工程学院，辽宁 沈阳 110819；2.东北大学 流程工业综合自动化国家重点实验室，辽宁 沈阳 110819）

0 引言

随着市场竞争的加剧，越来越多的企业将物流服务外包给专业的物流公司，物流公司则通过优化资源和网络来提供更有效率的物流服务。由于拥有更多的资源和大量的信息，第四方物流［1］（the Fourth Party Logistics，4PL）具有更广阔的发展前景，它依靠优秀的第三方物流（the Third Party Logistics，3PL）供应商、技术供应商、管理咨询以及其他增值服务供应商，为客户提供独特广泛的供应链解决方案，从而帮助企业有效地整合资源。

近年来，国内外学者对4PL 相关问题进行了一些研究。李秀等［2］设计了4PL 体系结构及其电子商务模式下的运作模式；Huang等［3］基于多重图和非线性整数规划研究了4PL的路径优化问题；Chen等［4］对4PL 中的活动指派问题进行了研究；王勇等［5］研究了4PL的作业整合问题。然而，物流网络对4PL系统的有效运作起关键作用。4PL 管理者需要根据客户的服务需求设计网络。4PL 网络设计问题指确定产品从供应点到需求点的网络结构，即通过选择3PL 服务节点和运输供应商来构建4PL网络。

“911”事件以来，人们越来越关注各种公共服务系统的安全性问题。由于自然灾害及人为等不安全因素的影响，4PL系统中的3PL 服务节点和运输供应商往往面临着不确定的中断风险，中断的发生可能使4PL系统的服务性能下降甚至瘫痪。因此，设计安全可靠的服务网络也是4PL 管理者必须考虑的问题。有关物流或供应链系统的安全性问题也得到学者的关注和研究。Peng等［6］对可靠的物流网络设计问题展开了研究；Meepetchdee等［7］研究了考虑鲁棒性和复杂性的物流网络设计问题；Klibi等［8］对鲁棒的供应链网络设计问题进行了很好的综述。弹复性［9-10］提供了一种研究系统安全性的新方法；Konak等［11］基于遗传算法设计弹复性的通讯网络；Wang等［12］对物流网络的弹复性进行了定义和分析，并强调网络冗余和可靠的物流线路是提高网络弹复性的重要因素；Miller-Hooks等［13］研究了运输网络的弹复性最大化问题，通过扩充故障前后线路的容量来增强网络抗击中断的能力；Liu等［14］研究了运输网络的保护问题，通过对运输线路的改造使其在故障状态下保持完好，从而改善整个网络的弹复性和鲁棒性。

目前，对物流网络可靠性设计问题的研究都只考虑单一运营周期。现实中，商品的需求量和供应量，以及3PL服务节点和运输供应商有关的成本、能力和故障概率等属性在不同时间段内往往不同，因此多周期的网络设计对4PL 更具有现实意义。一些学者已经对多周期物流网络的设计问题进行了研究。Shulman等［15］考虑有容量限制的工厂动态选址问题；Antunes等［16］通过模拟退火算法求解多周期的选址问题；Alumur等［17］研究了多周期逆向物流网络的设计问题；伍星华等［18］研究了再制造闭环物流网络的多周期优化设计问题；Ko 等［19］对3PL正反向集成的多周期物流网络设计问题进行了研究。上述关于多周期物流网络设计问题都是属于企业自营或者基于3PL的物流网络设计，并且都没有考虑网络的安全性。

本文对4PL 服务模式下的多周期物流网络设计问题进行研究，考虑3PL服务节点或运输供应商的随机中断，引入弹复性来描述网络在中断状态下的服务质量，即考虑了网络的安全性，并通过加固措施来提高网络的弹复性；建立了带有弹复性约束的多周期物流网络设计模型，选择3PL 物流服务节点和运输供应商，同时还确定是否对已选择的3PL 服务节点和运输供应商进行加固；根据问题模型的特点，设计了一种带邻域搜索的全局最好和声搜索（Neighborhood Search Global-best Harmony Search，NSGHS）算法，并通过随机生成的数值算例对算法进行测试，实验结果表明了该模型的合理性及算法的有效性。

1 问题描述

考虑4PL根据某一区域内多个周期（几个月、几个季度或者几年）的物流配送任务来构建的服务网络，包括供应节点、需求节点、3PL 服务节点（仓库、配送中心、港口等）和3PL 运输供应商。图1给出了4PL网络结构，商品通过3PL服务节点和运输供应商从供应点运输到需求点。此外，由于自然或人为因素的影响，3PL 服务节点或者运输供应商的服务可能发生中断，从而影响物流服务的质量。这里用网络的弹复性来描述系统在故障状态下的服务质量。

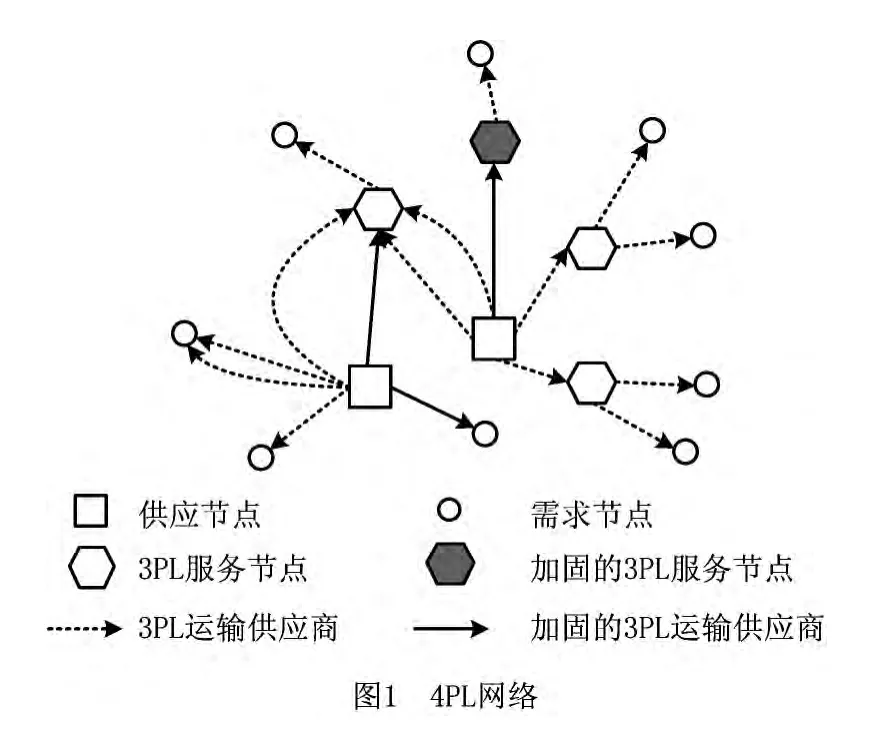
假设条件如下：

（1）3PL 服务节点具有处理费用、处理能力、构建成本、运作成本和加固成本（使其保持一定能力而投入的成本）等属性。在任意两地之间可能存在多个3PL 运输供应商，不同运输供应商的运输费用、运输能力、构建成本、运作成本和加固成本不同。3PL 服务节点和运输供应商在不同周期具有不同的属性值。

（2）3PL 服务节点和运输供应商发生故障的概率已知。另外，某周期内被加固的3PL 服务节点或者运输供应商在当前周期不会中断。

（3）每个需求点可由多个供应点提供商品。每个周期内供应点的最大供应量和需求点的需求量已知。

基于弹复性的4PL多周期网络设计问题，是指在每个周期内通过选择3PL 服务节点和运输供应商来构建物流服务网络，并同时决定是否对其进行加固，在满足一定弹复性水平要求的情况下最小化网络总成本。

2 问题建模

2.1 符号说明

已知4PL网络，V=L∪S∪U为节点集合，其中：L为需求节点的集合，S为供应节点的集合，U为3PL服务节点的集合；Kij为节点i和j之间3PL运输供应商的集合；T为周期集合。供应节点i∈S在周期t∈T的最大供应量为；需求节点j∈L在周期t∈T的需求量为。3PL 服务节点i∈U在周期t∈T的单位货物的处理成本、处理能力、固定运作成本、构建成本、加固成本和故障概率分别为和；节点i∈V和j∈V之间3PL运输供应商k∈Kij在周期t∈T的单位货物的运输成本、运输能力、固定运作成本、构建成本、加固成本和故障概率分别为和。

2.2 问题的模型

基于以上参数和变量，建立4PL 多周期弹复性网络设计模型如下：

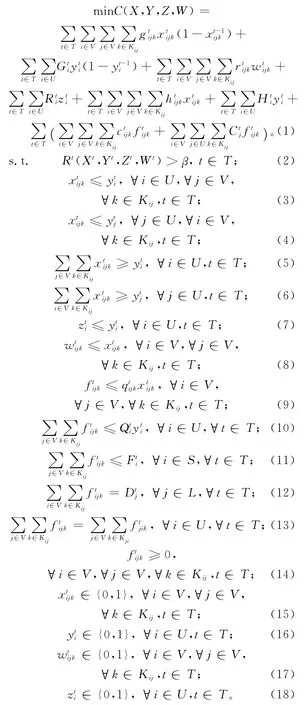
其中：目标函数（1）最小化网络的总成本，包括构建成本、加固成本、固定运作成本和运输处理成本；约束（2）确保各个周期网络的弹复性满足要求的水平β；约束（3）和约束（4）确保当3PL 服务节点没有被选择时，与其相连的3PL 运输供应商也不能被选择；约束（5）和约束（6）表示如果3PL 服务节点被选择，则必须保证至少分别有一个3PL 运输供应商运入商品和运出商品；约束（7）和约束（8）表示加固的3PL服务节点或者运输供应商必须是被选择的；约束（9）是3PL 运输供应商能力的限制；约束（10）是3PL服务节点处理能力的约束；约束（11）表示供应点的最大供应量；约束（12）表示对需求点的需求量必须得到满足；约束（13）保证3PL服务节点两端的流平衡；约束（14）是流量的非负条件；约束（15）～约束（18）表示二值的决策变量。

以上模型相比现有的多周期物流网络设计文献［15-19］，除了考虑网络的弹复性约束，还在目标函数中引入了加固成本，并同时确定网络中的3PL 服务节点和运输供应商的选择和加固。

2.3 4PL网络弹复性

弹性用来描述系统抗中断的能力，即在故障状态下系统仍然能够保持其功能的能力。在文献［11-13］中都将网络的弹性定义为网络在故障状态下对需求的满足率。4PL 网络的弹复性用来描述中断状态下对客户需求的满足能力。因此，4PL 网络在周期t的弹复性可以定义为

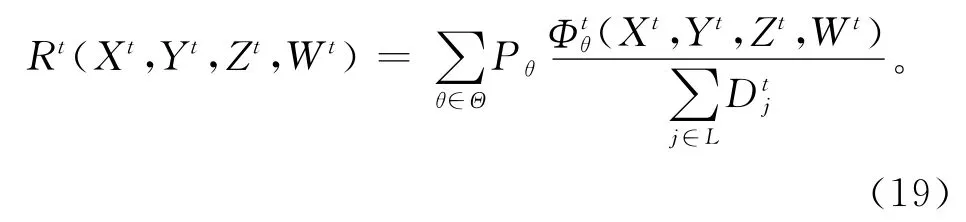
式中：Pθ表示故障状态θ发生的概率，Θ是故障状态的集合，表示故障状态θ∈Θ下网络在周期t对所有需求点的最大满足量，并通过如下模型确定：

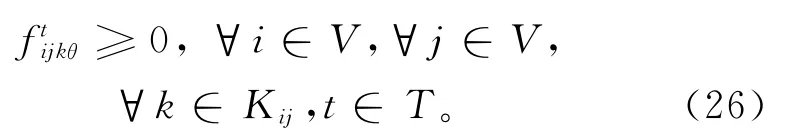
3 带邻域搜索的全局最好和声搜索算法

弹复性的4PL 多周期网络设计问题是经典网络可靠性设计问题的扩展，因此是NP-Hard的。为了有效求解大规模问题，本文设计一种NSGHS算法。

和声搜索（Harmony Search，HS）算法模拟自然界音乐演奏中寻找优美和声的过程，是由Geem等［20］提出的一种新的元启发式算法。算法首先产生M个和声放入和声记忆库；对新解的各个分量以概率PHMCR在和声记忆库内搜索，以概率1-PHMCR在分量值域中搜索，然后对在记忆库中搜索的分量以概率PPAR进行扰动，如果新和声优于记忆库中的最差和声，则替换之。如此循环，直至创作（迭代）的次数达到NI。由于HS算法具有结构简单、容易实现等特点，已经成功地解决了水资源网络设计［21］、零空闲流水线调度［22］、大学课程时间表［23］、传输网络扩容［24］和热电经济调度［25］等问题。目前HS算法的主要改进版本有改进和声搜索算法（Improved Harmony Search，IHS）［26］和全局最好和声搜索算法（Global-best Harmony Search，GHS）［27］等。IHS采用变化的扰动概率和扰动幅度，GHS则利用全局最好解扰动来改善HS搜索最优解的能力。

HS算法的性能在应用过程中已经得到了验证。因为HS算法通过逐个确定和声中的各个分量来产生新和声，更有利于对问题约束的处理，所以本文基于HS算法设计一种NSGHS算法，对问题进行求解。该算法将局部搜索引入GHS 算法，在利用GHS 算法生成新和声后，再对新和声以一定概率进行邻域搜索，从而进一步改善GHS算法的性能，能够对问题的解邻域进行有效的探索。

3.1 NSGHS算法的总体步骤

本文提出的NSGHS算法的主要步骤如下：

步骤1 初始化参数。包括和声记忆库的大小、和声记忆库考虑概率、音调微调概率和最大迭代次数。

步骤2 随机生成初始的和声记忆库，同时按照和声修复策略对和声进行修复（详见3.3节），评价记忆库中的和声（详见3.4节）。

步骤3 产生新的和声，并按照和声修复策略对和声进行修复（详见3.3节）。以概率PHMCR在记忆库中产生新和声的各个分量，以概率1-PHMCR在分量值域中进行搜索。对记忆库中产生的分量以概率PPAR取全局最优解中的对应分量。

以概率PL对新产生的和声执行邻域搜索。PL的取值随迭代次数变化，PL=PLmax-（PLmax-PLmin）×（gn／NI）。其中：gn为当前的代数，PLmax和PLmin分别表示概率的最大值和最小值。邻域搜索首先随机选择一个周期，然后随机选择下面的邻域操作之一产生新解：

邻域操作1 随机改变某一位的值；

邻域操作2 随机删除一条弧；

邻域操作3 随机删除一个点；

邻域操作4 随机插入一条弧；

邻域操作5 随机插入一个点。

步骤4 对新产生的和声进行评价，如果优于记忆库中的最坏和声，则替换最坏和声。

步骤5 若到达最大更新次数，则停止，否则转步骤3。

步骤6 对和声记忆库中最好的ω个和声（解）以大样本Monte Carlo进行仿真，重新评估网络的弹复性（详见3.5 节），从而得到最好解，算法结束。

3.2 和声的表示

如图2所示，和声（问题的解）采用2维数组表示。数组的行数为周期数，列数为所有潜在的3PL服务节点和运输供应商的数量之和。数组中的每一个数都对应某个3PL 的服务节点或运输供应商在某个周期的状态，“0”表示未选择，“1”表示选择，“2”表示选择并加固。具体来说：如果某3PL 服务节点i∈U在周期t∈T所对应的和声分量的值为“0”，则表示该节点未被选择，即；如果和声分量值为“1”，则表示该节点被选择，即如果和声分量值为“2”，则表示该节点被选择并加固，即。按照同样的方法可以确定和的值。可见，按照上述和声的表示方法进行解码得到的解（X，Y，Z，W），可自动满足约束（7）、约束（8）及约束（15）～约束（18）。

3.3 和声修复策略

为了使得到的解能够满足网络连通性约束（3）～约束（6），在初始化和声记忆库和产生新和声的过程中，需要对和声进行修复，策略如下：以供应点为起点，采用广度优先搜索依次确定和声中点和弧的对应分量的值，如果一个3PL 的服务节点j∈U有入弧、无出弧，则随机选择一个以j为起点的弧，并将和声中该弧的对应值设为1或2，即至少选择一个出弧。类似地，如果一个解中没有弧指向某需求节点j∈L，则选择类似的方法进行修复。

3.4 和声的评价函数

按上述和声的表示方法和修复策略所得到的解都满足网络的连通性约束，然后按下面方法对和声进行评价。

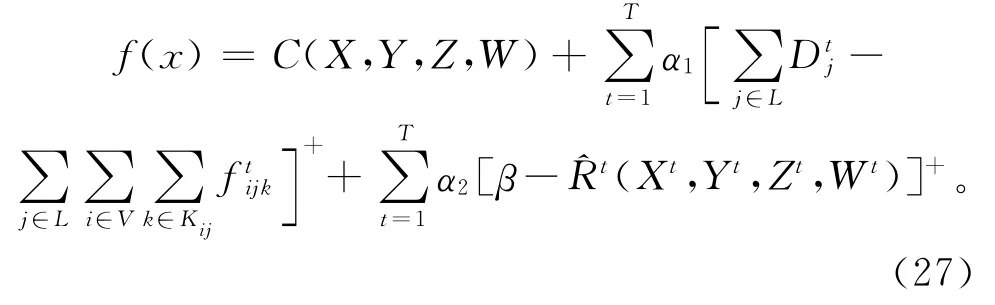
式中：C（X，Y，Z，W）为解（X，Y，Z，W）对应的目标函数值，对于每个周期，可以通过增加虚拟的起始节点和终止节点，将问题转化为网络的最小费用最大流问题，然后通过Bellman-Ford和Ford-Fulkerson相结合的方法进行求解，其中网络的流量约束（9）～约束（11）、约束（13）和约束（14）可自动满足。按照上述方法计算的过程中，新的和声只能不满足网络的弹复性约束（2）和需求满足约束（12），在评价和声时对这两个约束进行惩罚。是通过Monte Carlo仿真计算的网络弹复性的期望值（详见3.5节）；α1和α2为两个惩罚系数；（·）+表示如果括号内的值为正，则取该值，否则取0。

3.5 弹复性计算

NSGHS算法中每一次对和声进行评价，以及步骤6中对最好的ω个和声（解）进行精确评估时，都需要评估相应网络在各个周期的弹复性，这里采用Monte Carlo仿真的方法进行评估，网络在周期t的弹复性评估的具体步骤如下：

步骤1 根据周期t内3PL 服务节点和运输供应商的故障概率，产生N组相互独立的故障状态样本。

步骤2 对于每一种故障状态，基于标号法计算网络的最大流量，得到所有需求点的最大满足量。

步骤3 对各种故障状态及所有需求点的最大满足量与实际需求量的比值进行平均，得到网络在周期t的弹复性的期望值，即

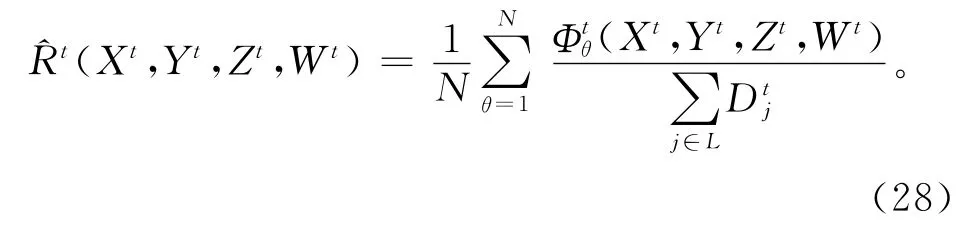
4 仿真分析

为了测试NSGHS算法的有效性，对随机产生的问题进行测试。算法采用MATLAB 语言编码，实验环境为Intel Core 2Quad 2.66GHz台式机，内存2.00GB。

4.1 实验数据的生成

随机生成小、中、大三种不同规模的10个算例进行实验，具体如表1所示。其中，问题的各个参数都按照表2中给出的均匀分布随机产生。

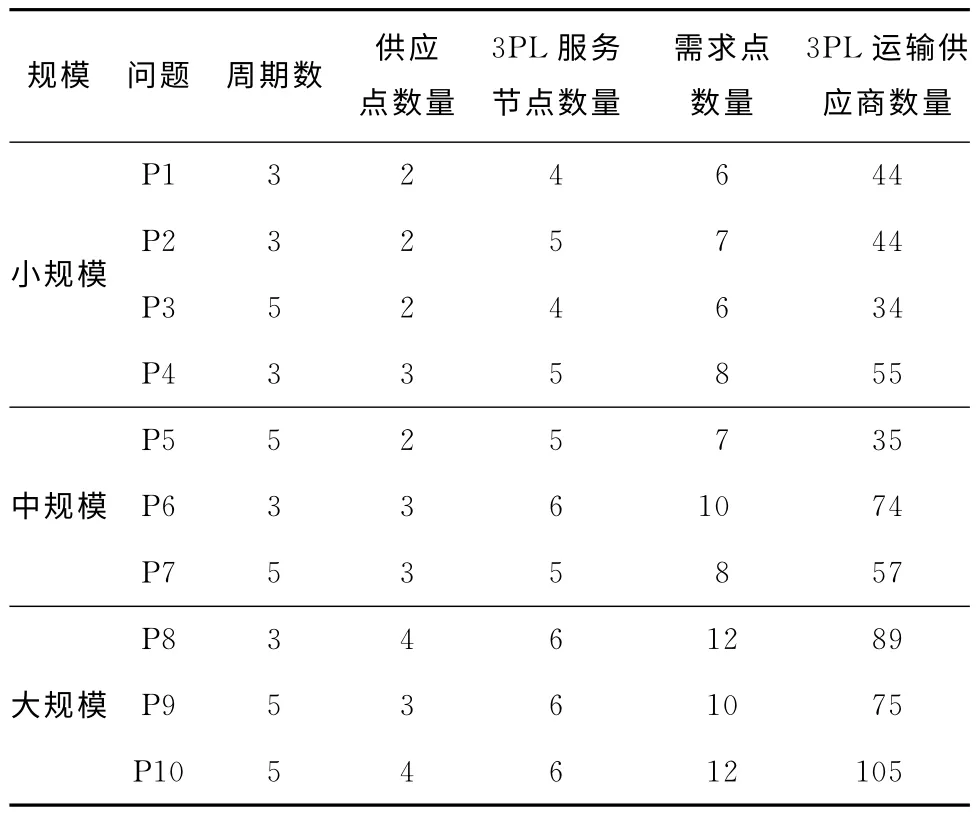
表1 问题的规模

表2 问题参数的均匀分布区间

4.2 实验结果与分析

为了测试NSGHS算法的性能，对不同规模的问题进行求解（所有问题弹复性水平取0.6），结果与传统的HS算法、IHS算法［26］、GHS算法［27］进行对比，其中所有算法均采用相同的修复策略生成新的和声。算法的参数设置如下：NSGHS 的和声记忆库的大小为20，和声记忆库考虑概率取0.98，音调微调概率取0.01，局部搜索概率的最大值和最小值分别为0.9 和0.2；HS 的和声记忆库的大小为20，和声记忆库考虑概率取0.95，音调微调概率取0.01；IHS的和声记忆库的大小为20，和声记忆库考虑概率取0.98，音调微调概率的最大值和最小值分别为0.01和0.000 1；GHS的和声记忆库的大小为20，和声记忆库考虑概率取0.98，音调微调概率取0.01；为了公平比较，各个算法取相同的迭代次数2 000。

对每个问题的每种算法分别独立运行20 次。表3给出了算法运行结果的对比。其中，任一算法的平均值改进率定义为

从表3 可见，对于所有问题，NSGHS 的最好值、最差值、平均值、平均值改进率和平均偏差率都优于其他算法，而几种算法的标准差百分比和CPU运行时间则没有明显差别。此外，随着问题规模的增大，NSGHS的平均值改进率有上升的趋势，平均偏差率也没有出现下滑的趋势。可见，随着问题规模的增大，NSGHS 算法仍然能够保持稳定的性能。

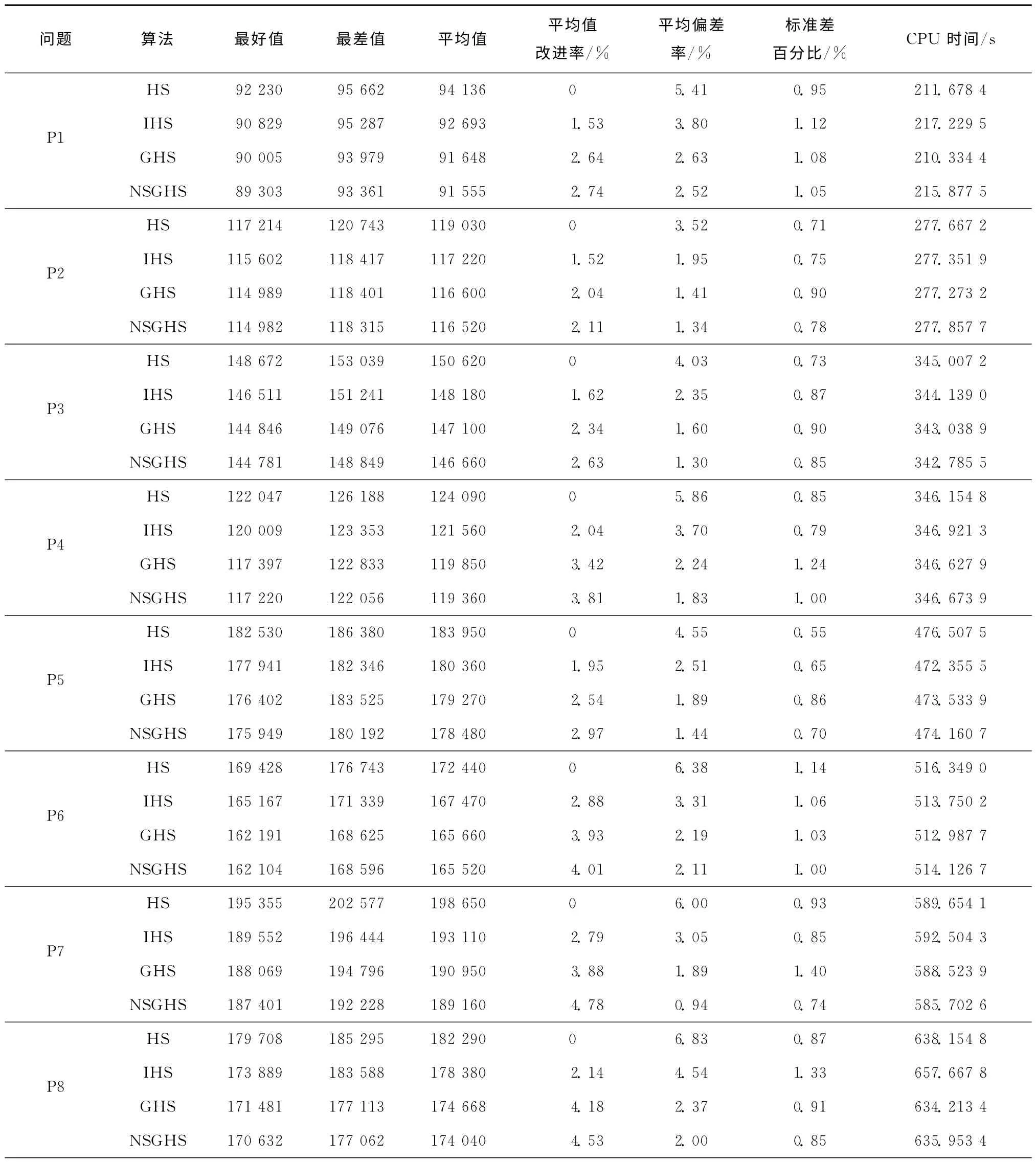
表3 求解规模不同问题的算法对比结果

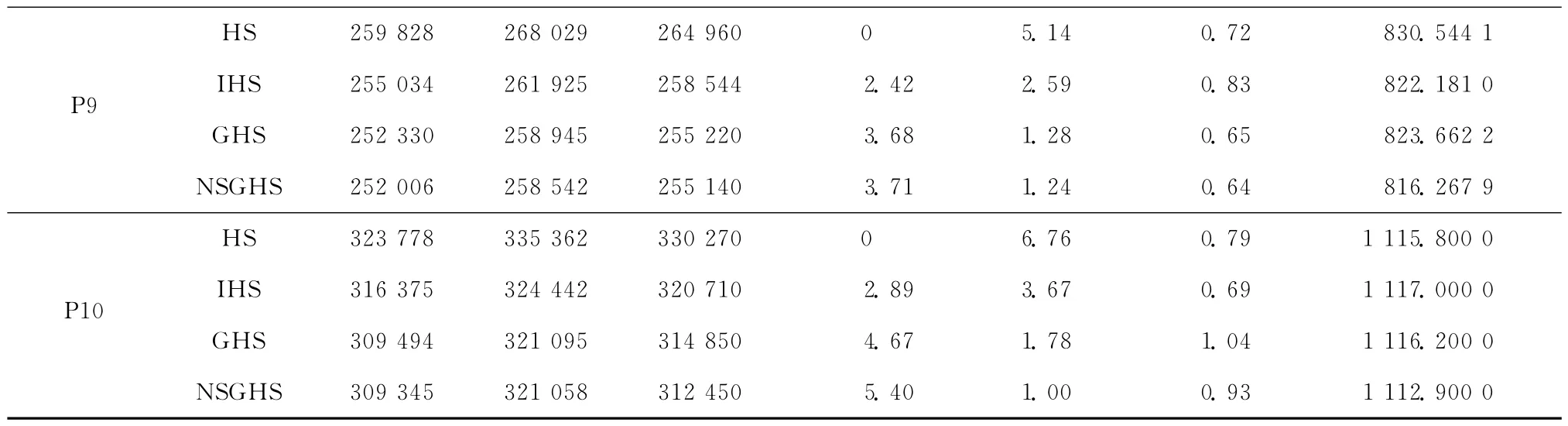
续表3

图3所示为对求解问题P3各个算法运行20次的最优解的目标均值随迭代次数变化的曲线。由图3可见，随着迭代次数的变化，GHS算法与IHS算法的性能接近，而NSGHS算法的性能明显优于其他算法。

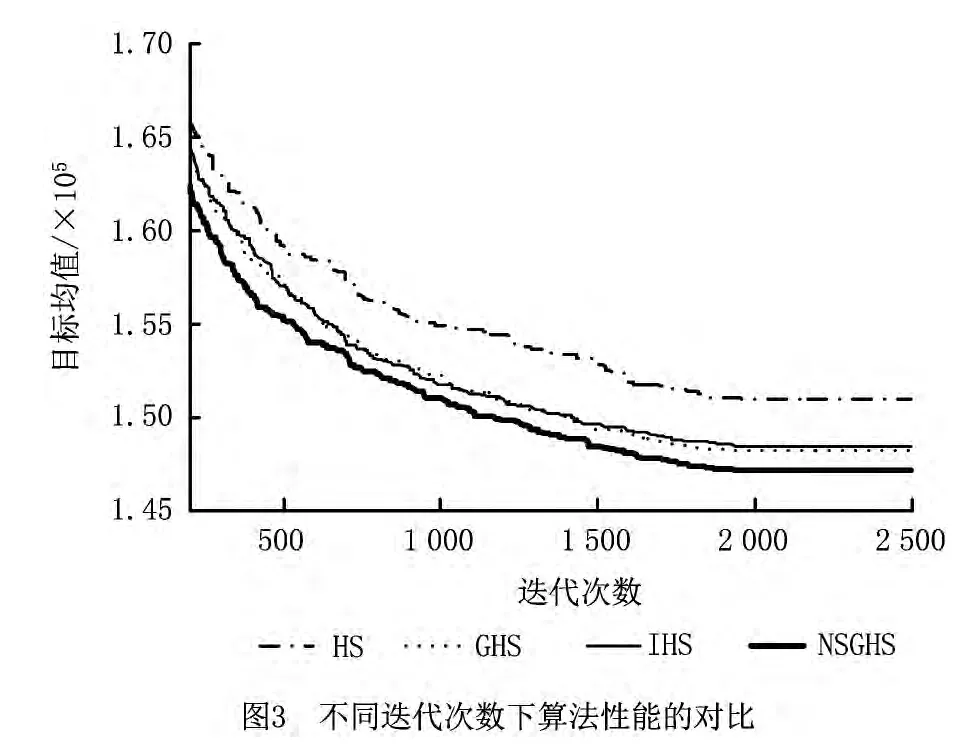
表4所示为问题P3在不同弹复性指标下的详细结果，包括目标值、构建成本、加固成本、运作成本和运输和处理成本。从表4可见，随着弹复性值的增大，构建成本、加固成本和运作成本都增加，运输和处理成本并不随弹复性的增大而增加。

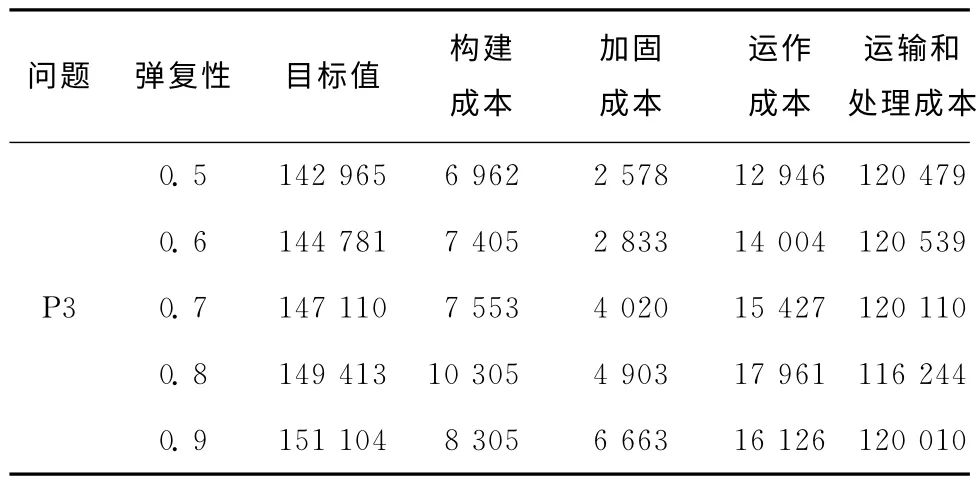
表4 问题P3在不同弹复性下的结果

为了分析NSGHS的参数对算法性能的影响，针对问题P3，对影响算法性能的主要参数进行测试，包括和声记忆库考虑概率PHMCR、记忆库大小M和局部搜索概率PL。将算法20 次运行的平均偏差率作为性能指标，其中平均偏差率定义为（平均值-最好值）／最好值×100%。图4所示为PHMCR对性能的影响。其中：PHMCR取值为0.9～0.99，平均值偏差率随PHMCR的增大而减小，当PHMCR为0.98时，平均值偏差率达到最小值。图5所示为记忆库大小对算法性能的影响。可见，随着记忆库规模的增大，平均偏差率变大。表5所示为局部搜索概率对算法性能的影响。可见，当局部搜索概率的最大值和最小值分别为0.9和0.2时，平均偏差率最小。

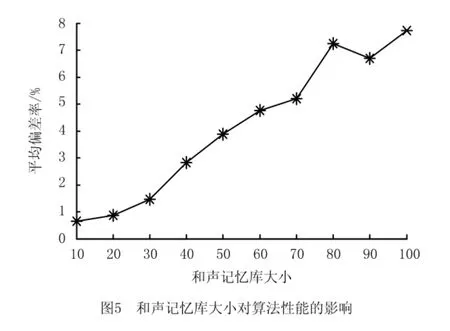
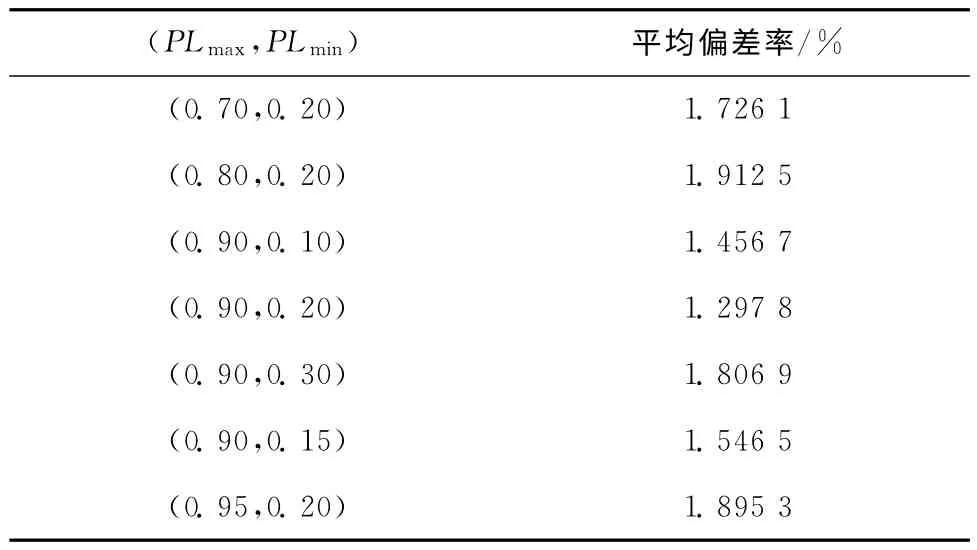
表5 局部搜索概率对算法性能影响

5 结束语

本文研究基于弹复性的4PL 多周期网络设计问题，给出了考虑弹复性的4PL 多周期网络设计模型，在一定的弹复性要求下最小化网络总成本。根据问题模型的特点，设计了一种NSGHS算法，通过数值仿真实例验证了模型的合理性和算法的有效性，表明NSGHS算法的性能优于传统HS算法、文献［26］中的IHS算法和文献［27］中的GHS算法，同时也分析了NSGHS的参数对其性能的影响。

随着4PL 的发展，未来研究可能考虑多商品、多种中断类型，以及更复杂的网络结构。

［1］GATTORNA J.Strategic supply chain alignment：best practice in supply chain management［M］.Hampshire，UK：Gower Publishing Company，1998：425-445.

［2］LI Xiu，YING Weiyun，LIU Wenhuang，et al.Research on architecture and operation of 4PL［J］.Computer Integrated Manufacturing Systems，2004，10（10）：1233-1237（in Chinese）.［李 秀，应维云，刘文煌，等.第四方物流的体系结构和运作模式研究［J］.计算机集成制造系统，2004，10（10）：1233-1237.］

［3］HUANG M，TONG W，WANG Q，et al.Immune algorithm based routing optimization in fourth-party logistics［C］／／Proceedings of IEEE Congress on Evolutionary Computation.Washington，D.C.，USA：IEEE，2006：3029-3034.

［4］CHEN K H，SU C T.Activity assigning of fourth party logistics by particle swarm optimization-based preemptive fuzzy integer goal programming［J］.Expert System with Application，2010，37（5）：3630-3637.

［5］WANG Yong，ZHAO Hua，LI Yong.Tabu search algorithm for optimization model of integration of job of 4th party logistics［J］.Journal of Systems Engineering，2006，21（4）：143-149（in Chinese）.［王 勇，赵 骅，李 勇.用禁忌算法求解第四方物流作业整合优化模型［J］.系统工程学报，2006，21（4）：143-149.］

［6］PENG P，SNYDER L V，LIM A，et al.Reliable logistics networks design with facility disruptions［J］.Transportation Research：Part B，2011，45（8）：1190-1211.

［7］MEEPETCHDEE Y，SHAH N.Logistical network design with robustness and complexity considerations［J］.International Journal of Physical Distribution &Logistics Management，2007，37（3）：201-222.

［8］KLIBI W，MARTEL A，GUITOUNI A.The design of robust value-creating supply chain networks：a critical review［J］.European Journal of Operational Research，2010，203（2）：283-293.

［9］HOLLNAGEL E，WOODS D D，LEVESON N.Resilience engineering：concepts and precepts［M］.Aldershot，UK：Ashgate Publishing Company，2006：35-41.

［10］MADNI A M，JACKSON S.Towards a conceptual framework for resilience engineering［J］.IEEE System Journal，2009，3（2）：181-191.

［11］KONAK A，BARTOLACCI M R.Designing survivable resilient networks：a stochastic hybrid genetic algorithm approach［J］.Omega-International Journal of Management Science，2007，35（6）：645-658.

［12］WANG D W，IP W H.Evaluation and analysis of logistics network resilience with application to aircraft servicing［J］.IEEE System Journal，2008，3（2）：166-173.

［13］MILLER-HOOKS E，ZHANG X，FATURECHI R.Measuring and maximizing resilience of freight transportation networks［J］.Computers &Operations Research，2012，39（7）：1633-1643.

［14］LIU C，FAN Y，ORDÓÑEZ F.A two-stage stochastic programming model for transportation network protection［J］.Computers &Operations Research，2009，36（5）：1582-1590.

［15］SHULMAN A.An algorithm for solving dynamic capacitated plant location problems with discrete expansion sizes［J］.Operations Research，1991，39（3）：423-436.

［16］ANTUNES A，PEETERS D.On solving complex multi-period location models using simulated annealing［J］.European Journal of Operational Research，2001，130（1）：190-201.

［17］ALUMUR S A，NICKEL S，SALDANHA-DA-GAMA F，et al.Multi-period reverse logistics network design［J］.European Journal of Operational Research，2012，220（1）：67-78.

［18］WU Xinghua，WANG Xu，DAI Ying，et al.Multi-period optimal design model for closed loop remanufacturing logistics network［J］.Computer Integrated Manufacturing Systems，2011，17（9）：2015-2021（in Chinese）.［伍星华，王 旭，代应，等.再制造闭环物流网络的多周期优化设计模型［J］.计算机集成制造系统，2011，17（9）：2015-2021.］

［19］KO H J，EVANS G W.A genetic algorithm-based heuristic for the dynamic integrated forward／reverse logistics network for 3PLs［J］.Computers and Operations Research，2007，34（2）：346-366.

［20］GEEM Z，KIM J，LOGANATHAN G.A new heuristic optimization algorithm：harmony search［J］.Simulation，2001，76（2）：60-68.

［21］GEEM Z W.Optimal cost design of water distribution networks using harmony search［J］.Engineering Optimization，2006，38（3）：259-277.

［22］WU Lei，PAN Quanke，SANG Hongyan，et al.Harmony search algorithms for no-idle flow shop scheduling problems［J］.Computer Integrated Manufacturing Systems，2009，15（10）：1960-1967（in Chinese）.［武 磊，潘全科，桑红燕，等.求解零空闲流水线调度问题的和声搜索算法［J］.计算机集成制造系统，2009，15（10）：1960-1967.］

［23］AL-BETAR M A，KHADER A T.A harmony search algorithm for university course timetabling［J］.Annals of Operations Research，2012，194（1）：3-31.

［24］VERMA A，PANIGRAHI B K，BIJWE P R.Harmony search algorithm for transmission network expansion planning［J］.Generation，Transmission &Distribution，2010，4（6）：663-673.

［25］KHORRAM E，JABERIPOUR M.Harmony search algorithm for solving combined heat and power economic dispatch problems［J］.Energy Conversion and Management，2011，52（2）：1550-1554.

［26］MAHDAVI M，FESANGHARY M，DAMANGIR E.An improved harmony search algorithm for solving optimization problems［J］.Applied Mathematics and Computation，2007，188（2）：1567-1579.

［27］OMRAN M G H，MAHDAVI M.Global-best harmony search［J］.Applied Mathematics and Computation，2008，198（2）：643-656.