双向随机多策略变异的自适应差分进化算法

孔祥勇，高立群，欧阳海滨，邵煜博

（东北大学 信息科学与工程学院，辽宁 沈阳 110004）

0 引言

差分进化（Differential Evolution，DE）［1］算法是近年来发展起来的一种基于群体智能的进化算法，该算法借助种群内个体间的差异，通过合作和竞争实现种群进化。DE 算法最初为解决切比雪夫多项式问题而提出，其后在复杂函数优化方面表现出了很强的优势，得到了广泛的关注和应用［2-5］。DE主要包括变异、交叉和选择操作，与遗传算法相比，DE采用实数编码，降低了遗传操作的复杂性，其原理简单，受控参数少，易于理解和实现，能够随机、并行、直接地在连续空间中进行启发式搜索。由于采用贪婪选择方式，与其他进化算法一样，DE 在搜索的后期，随着种群多样性的下降，容易出现早熟、陷入局部最优和收敛精度不高的问题。

为提高算法性能，许多学者对DE 进行了改进，主要包括以下几方面：设计新变异算子、自适应调整参数、引入高效搜索策略、与其他优化算法结合、实现多策略多种群并行搜索等。现有的变异算子或全局搜索能力强，或局部搜索能力强，或适于解决变量可分离函数，或适于解决变量耦合的复杂函数，都有其局限性，仅适用于一定的范围，而实际工程问题十分复杂，内部性质无法预知，很难选择合适的变异算子。多变异策略及参数的自适应调整能够根据问题和搜索过程实时调整相关操作，使其满足进化的需要，现已成为差分进化算法发展的趋势。

Qin等［6］2009年提出一种自适应差分进化算法（Self-adaptive DE，SaDE），通过对之前的个体进行学习，自适应地选择合适的变异策略和参数，从而提高算法的优化性能。Mallipeddi等［7］于2011 年提出EPSDE（DE with an ensemble of mutation strategies and control parameters）算法，将一系列不同的变异策略和参数进行组合，构建了一个候选变异策略库，进化过程中不同变异策略与参数并存，通过竞争产生子代个体。Wang 等［8］于2011 年经过深入研究现有变异算子和参数的性质，将复合策略应用到DE中，提出复合差分进化算法（Composite DE，CoDE）。CoDE随机选择三种不同变异策略中的一种进行变异操作，产生子代个体。虽然EPSED 和CoDE算法采用了多算子变异策略，但缺乏必要的学习过程，不能根据进化过程进行相关策略的自适应选择。SaDE 算法能够根据之前的经验适时调整变异策略和参数的选择概率，但该算法的学习过程较复杂，同时在实际应用过程中的参数设置比较困难。

针对以上多策略变异算法的不足，通过深入分析现有变异算子的特点和不足，提出双向随机多策略变异的自适应差分进化算法（Adaptive DE with Bidirectional Randomly Multi-mutation strategy，ADE-BRM）。ADE-BRM 算法主要包含以下三方面的改进：①提出一种新的多策略变异算子，借助符号函数将几种典型变异算子进行融合，在进化过程中充分发挥各算子的优势；②将原有变异率用-1～1之间的随机数取代，使搜索能在两个方向上进行，从而克服进化后期种群多样性下降导致早熟误收敛的问题，同时减少了算法参数，提高了算法的实用性；③设计了交叉率的两区间选择策略，在进化过程中不断学习，从而实现自适应调整，解决了该参数设置困难的问题。与现有的典型算法进行对比实验，结果验证了ADE-BRM 算法的优越性。

1 基本差分进化算法

对于一个极小化问题，通常采用如下模型进行描述：

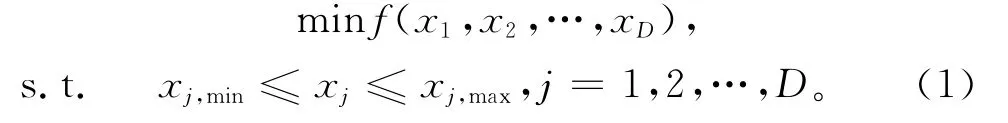
式中：D为优化问题自变量的维数，xj，max和xj，min分别表示第j维分量xj取值的上限和下限。

原始差分进化算法的具体流程如下［1］：

（1）初始化 DE 采用NP个D维向量作为 每一代的种群，初始种群应尽可能覆盖整个搜索空间，通常采用随机生成的方式。

（2）变异 DE 通过差分实现个体变异，最常用的策略是随机选取种群中的两个个体，将其向量差与变异率F相乘，而后与待变异个体xr0，g进行向量合成。

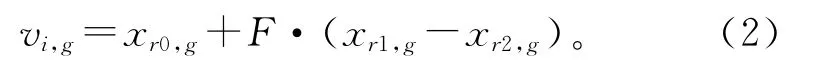
式中r0，r1，r2为｛1，2，…，NP｝中不同于i的两两互异的三个随机整数。

（3）交叉 DE将目标个体xi，g及其对应的变异个体vi，g进行交叉，进而产生子代个体ui，g，

式中：CR为交叉率，r为0～1之间的随机数，jrand为1～D之间的随机整数。

（4）选择 DE 采用贪婪原则决定是否保留子代个体进入下一代的进化过程，两者中的适应度值较大者将在下一代种群中占一席之地，从而保证下一代种群中的所有个体都不差于当前种群中的对应个体。

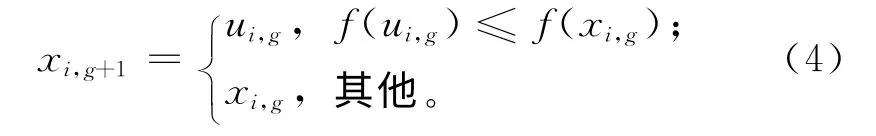
（5）终止判断 若满足终止条件，则停止搜索，输出结果；否则，继续执行变异、交叉和选择等操作。

2 双向随机多策略变异的自适应差分进化算法

通过分析现有典型变异算子的特点和不足，针对单一变异算子难以均衡局部搜索和全局搜索的问题，提出多策略变异算子，同时针对实际问题中参数设置困难的问题，从算法实用性的角度出发，设计了双向随机搜索策略和交叉率CR的两区间自适应选择策略。

2.1 多策略变异算子

变异操作是差分进化算法的主要部分，在很大程度上影响算法的性能。目前常用的四类典型变异算子有：

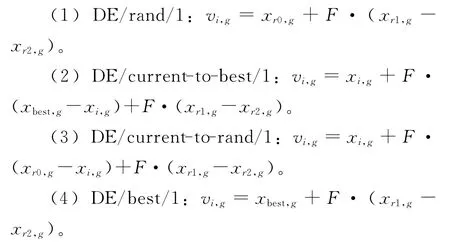
式中：r0，r1和r2为｛1，2，…，NP｝中不同于i的两两互异的三个随机整数，xi，g和xbest，g分别表示当前个体以及到目前为止找到的全局最优个体。

DE／rand／1是目前应用最成功、最广泛的一类变异算子，该算子能够随机地在全局进行寻优，但由于缺少必要的全局最优信息，其收敛性较差；DE／best／1以当前种群的全局最优个体作为基，在小范围内实现局部寻优，其收敛速度快、精度高，然而局部寻优往往导致种群陷入局部最优，很难跳出；为平衡局部寻优 和全局寻优，DE／current-to-best／1 和DE／current-to-rand／1采用半贪婪策略，在当前个体附近局部寻优，同时向全局最优个体或随机个体靠近，其跳出局部最优的能力强于DE／best／1，但全局搜索能力低于DE／rand／1。四类典型变异算子各有其特点和不足，有些算子的全局寻优能力强，但局部探索能力弱，进化后期收敛精度差；与此同时，有些算子的局部探索能力强，能在较小范围内找到精度较高的解，但该类算子的开发能力弱，容易早熟和陷入局部最优。

虽然研究者从不同角度设计了许多变异算子，取得了良好的优化效果，在一定程度上提高了算法的性能，但进化过程中全局寻优和局部寻优作为一对矛盾体，很难在单一的变异算子中得到均衡。针对以上问题，本文提出一种基于符号函数的多策略变 异（Bidirectional Randomly Multi-mutation，BRM）算子：

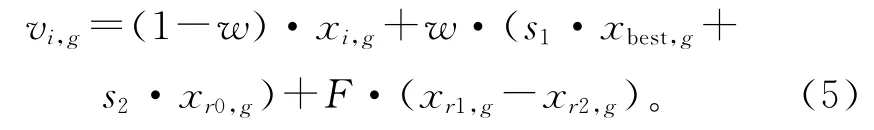
式中：w为0～1之间的随机数，s1和s2均为符号函数，定义为

BRM 算子采用算术交叉方式，将当前个体、最优个体和随机个体进行组合，外加差向量扰动，产生一个变异个体。全局最优个体能够为种群中其他个体的进化指明大致方向，加快种群的收敛；与此同时，为防止种群陷入局部最优、造成误收敛，引入一个不同于当前个体的随机个体，以增加找到更优个体和跳出局部最优的可能性。与现有的变异算子相比，BRM 算子增大了种群寻优的范围，能够很好地保持种群的多样性，进而提高算法的寻优性能，BRM 算子多策略变异的具体过程如下：

（1）当s1=s2=1时，式（6）可表示为vi，g=（1-w）·xi，g+w·（xbest，g+xr0，g）+F·（xr1，g-xr2，g）。当前个体与最优个体和随机个体构成的组合个体进行算术交叉，产生变异个体。该变异个体同时向最优个体和随机个体靠近，在收敛性和多样性上得到均衡。

（2）当s1=1，s2=0时，式（6）可以表示为vi，g=（1-w）·xi，g+w·xbest，g+F·（xr1，g-xr2，g）。BRM 算子转化为DE／current-to-best／1算子，通过向全局最优个体学习，加快算法收敛。在极限情况w=1时，DE／current-to-best／1又变为DE／best／1算子。因此，从整体上看，该算子的搜索特性类似于DE／best／1算子。

（3）当s1=0，s2=1时，式（6）可以表示为vi，g=（1-w）·xi，g+w·xr0，g+F·（xr1，g-xr2，g）。BRM算子转化为DE／current-to-rand／1 算子，通过向随机个体学习，增加种群的多样性。在极限情况w=1时，DE／current-to-rand／1变为DE／rand／1 算子。因此，从整体上看，该算子的搜索特性类似于DE／rand／1算子。

（4）当s1=s2=0时，式（6）可以表示为vi，g=（1-w）·xi，g+F·（xr1，g-xr2，g）。当前个体通过自身的伸缩产生变异个体时，在自身附近的超立方体空间中进行局部搜索能够提高解的精度。

由以上分析可知，BRM 算子中的四种变异策略包含了现有的几类典型变异算子的搜索特性，能够互相弥补各自的不足，均衡种群收敛性与多样性以及局部搜索与全局搜索之间的矛盾。与其他多策略变异相比，BRM 算子原理简单、易于实现，同时相对于固定F值，随机数w能够增加搜索范围，提高种群的多样性。

变异交叉产生的子代个体可能会跳出事先设定的变量空间，因此需要对这种越界情况进行处理。本文结合常用的随机产生法和中值法，提出一种新的变量越界处理方法。当某维变量发生越界时，在其对应的目标个体值与对应边界之间随机取值，同时针对全局最优点可能位于边界的情况，以一定概率取边界值，具体处理方法如下：

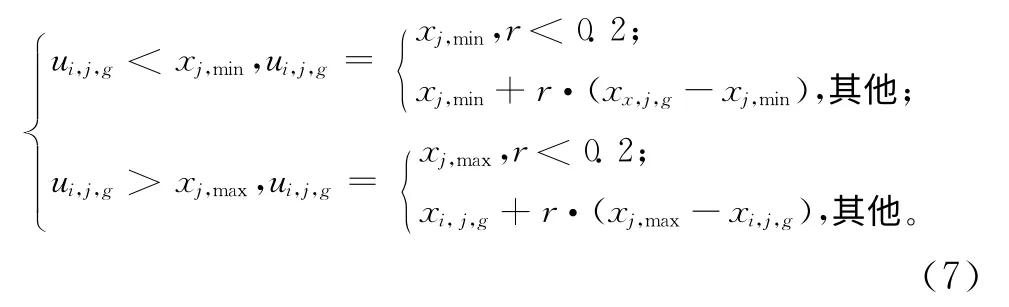
2.2 双向随机搜索策略

DE算法的优化性能在很大程度上取决于变异过程，不合适的变异策略和参数值可能导致算法误收敛和早熟。如何设置最佳参数值，使其满足进化搜索的需要，成为研究的重点之一。

作为DE算法中最重要的参数F，在进化前期应尽可能大，以扩大搜索的范围，尽快到达全局最优点附近，防止陷入局部最优；进化后期种群逐渐聚集在全局最优点附近，此时无需再进行大范围搜索，应进行小范围局部搜索，以提高解的精度，找到全局最优解，此时F值尽可能小。许多学者对F的取值进行了研究，文献［9-10］分别选择区间［0.5，1］和［0.4，0.95］作为F的最佳参考范围，而文献［1］认为F小于0.4 或大于1.0 有时也是有效的。文献［11］通过实验得出结论，F≤1 时算法通常能够快速、稳定地收敛到最优点，但F必须大于某一值，以防止种群早熟收敛到局部最优点。尽管有理论证明，将F转化为高斯随机数能使种群在有限长的时间收敛到全局最优点，但仍不能明显改善DE 算法的性能。经过分析上述F的参考范围，可得出以下结论：选取F∈［0，1］是合理的。双向随机优化理论［12］证明，如果正向搜索不能得到期望的优化效果，则反向搜索会以更高的概率使所得解得到优化，因此F值的取值范围从［0，1］扩展到［-1，1］是合理的。

由于实际问题的复杂性和不可预见性，参数的设定比较困难，而且很难判断设计的参数是否合适。为解决上述问题，本文从算法实用性的角度出发，在以往参考值的基础上提出双向随机搜索策略，舍弃了原有的变异率F值，而用-1～1的正负随机数取代。

正负随机数使搜索能够在两个方向上进行，这样可以克服进化后期种群多样性下降的问题，提高收敛到全局最优和跳出局部最优的可能性，同时简化了参数F的复杂设计过程，提高了算法的实用性。

综合式（5）、式（6）和式（8），BRM 最终可描述为

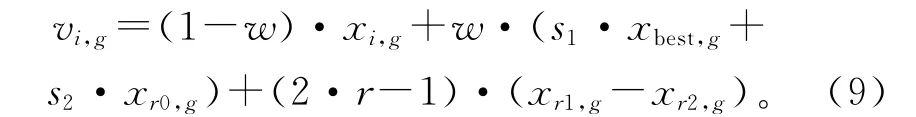
2.3 交叉率CR 的自适应选择

交叉率CR表示变量发生变异的概率，能够反映子代从父代直接继承信息的概率。较大的CR值使子代在很大程度上依赖于变异过程，而只从父代继承较少的信息，这样能够实现较大范围的全局搜索，提高跳出局部最优的可能性；反之，如果子代在父代周围进行局部搜索，则需CR取较小值，这样能够加快算法收敛，提高解的精度。

Gömperle等［11］认为，CR的最佳 取值区间在0.3～0.9之间。为适应实际需要，研究者对CR值进行了自适应设计，例如：Zhang等［13］提出自适应差分进化JADE算法（adaptive DE），将CR转化为正态随机数，在进化过程中不断调整分布的均值；Janez Brest等［14］根据随机数概率对CR随机赋值，实现了CR的自适应调整。此外，文献［10，15］从问题类型的角度指出：对于变量可分离函数，较小的CR值区间［0，0.2］有利于种群的搜索；但当变量之间相互耦合、函数为多峰值函数时，小的CR值不再奏效，CR应取［0.9，1］之间的较大值。文献［16］选择两个离散区间作为取值范围，但仅在初始取值时进行参考，在搜索过程中该参数确定不变，无法根据进化需要进行调整。

基于以上研究结果，本文提出交叉率CR的两区间自适应选择策略：设计两个正态分布并限定在一定区间内，然后通过学习自适应地更新每个区间被选择的概率，以适应问题的类型和进化搜索的需要。CR1为区间［0.05，0.15］内的正态随机分布N（0.1，0.025），CR2为区间［0.85，0.95］内的正态随机分布N（0.9，0.025）。任意一个个体产生实验个体时所使用的交叉率CR（i）由下式产生：

式中：pc表示在CR1取值的概率，其初始值为0.5，pc每隔一个学习周期（即LP代进化过程）更新一次，具体学习过程如下所述。

由式（3）和式（10）可知，变异个体和目标个体交叉时使用的交叉率是在两个区间内随机选择的，选择概率由pc决定。式（4）中，若子代个体取代父代个体进入下一代进化，则个体更新成功；反之，更新失败。一个学习周期内，分别记录交叉率在区间CR1和区间CR2内取值的次数以及个体更新成功的次数，并计算个体更新成功率，进而得到CR在每个区间取值的概率，具体计算如式（11）所示。某一学习周期内，在某个区间取值并且个体更新成功的比例越大，说明该区间的CR值更适合当前的进化环境，该区间被选择的概率就越大。

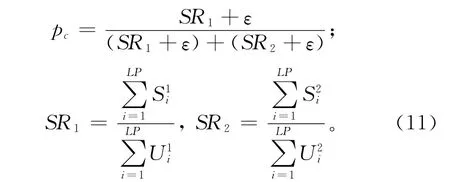
式中：SR1和SR2分别表示在CR1和CR2取值进行交叉时，个体更新成功的比例；U1i和U2i，S1i和S2i分别表示一个学习周期的第i代进化过程中，在CR1和CR2取值的次数以及个体更新成功的次数。为防止CR在某一区间取值的概率为0，在计算概率时加入了一个很小的数ε，一般可取ε=0.01。

交叉率的两区间自适应选择策略，减少了复杂的参数选取过程，能够在搜索过程中根据实际问题和进化的需要自适应地调整CR值，从而提高算法的实用性和寻优性能。

2.4 ADE-BRM 算法的具体实现步骤

综合以上对DE 的改进，双向随机多策略变异的自适应差分进化算法的具体流程如下：

步骤1 设置算法的初始参数，主要包括种群规模、学习周期、种群最大进化代数或最大函数调用次数、自变量的范围。随机生成初始种群，并设置当前进化代数t=1，当前学习代数lp=0。

步骤2 计算种群中个体的适应度值，更新最优个体。

步骤3 如果满足终止准则，则输出当前最优个体作为最优解；否则转步骤4，继续执行进化操作。

步骤4 判断当前学习代数lp是否等于学习周期LP，若满足，则执行步骤5；否则，转步骤6。

步骤5 按照2.3节的方法，更新CR区间选择概率pc，并令lp=0。

步骤6 用式（9）对当前种群进行变异操作。

步骤7 根据式（10）和式（11），每个个体生成相应的交叉概率，并分别记录交叉率在区间CR1和区间CR2内取值的次数，并用式（3）对变异后的个体进行交叉操作。

步骤8 采用贪婪准则更新种群，记录对应的更新成功的次数。

步骤9 新种群产生后，令t=t+1，lp=lp+1，转步骤2。

3 实验仿真与结果分析

为验证ADE-BRM 算法的性能，将其应用到文献［13］的13个多维标准测试函数中，优化结果与现有的几种经典多策略DE 算法进行对比，同时研究变异算子及参数对算法性能的影响，给出参数的参考取值。所有实验均采用MATLAB 7.50 实验仿真软件，在操作系统为Window XP SP3、主板CPU为Intel（R）Core 2Quad＠2.66GHz、内存为4G的电脑上独立运行。

3.1 测试函数特性简析

文献［13］中13个多维标准测试函数的全局最优值均接近或等于0，其函数特点简要介绍如下：f1～f4为单峰值函数，只有一个最优点；Rosenbrock函数f5在自变量为2～3维时是单峰函数，当自变量的维数增大时，函数f5的极小值数目随之增加，同时其全局最小值位于抛物线形的山谷中，该山谷容易找到，但由于谷内函数值变化较小，很难找到全局最小值；f6是一个非连续的单峰值阶梯函数；f7是复杂的噪声函数；f8～f13是多峰函数，有多个最优点，且最优点的个数随维数的增加呈指数趋势增加。对于一般优化算法，维数越高，越难找到多峰函数的最优点。

3.2 算法优化结果对比分析

实验中标准测试函数的维数取10 和30，选择近期提出的SaDE［6］，EPSDE［7］，CoDE［8］，ACoDE［8］与ADE-BRM 算法四种经典多策略DE算法作对比实验，进行30次独立运行，以验证其有效性。为保证对比实验的合理性，基于计算复杂性考虑，当问题的维数为D时，设定每种算法的最大函数调用次数为10 000D。实验中，四种对比算法的参数值按照原文进行设置，ADE-BRM 算法中的种群规模分别取30和60，学习周期LP=75。表1所示为相关的仿真对比结果，黑体加粗表示ADE-BRM 算法不劣于其他算法的部分。

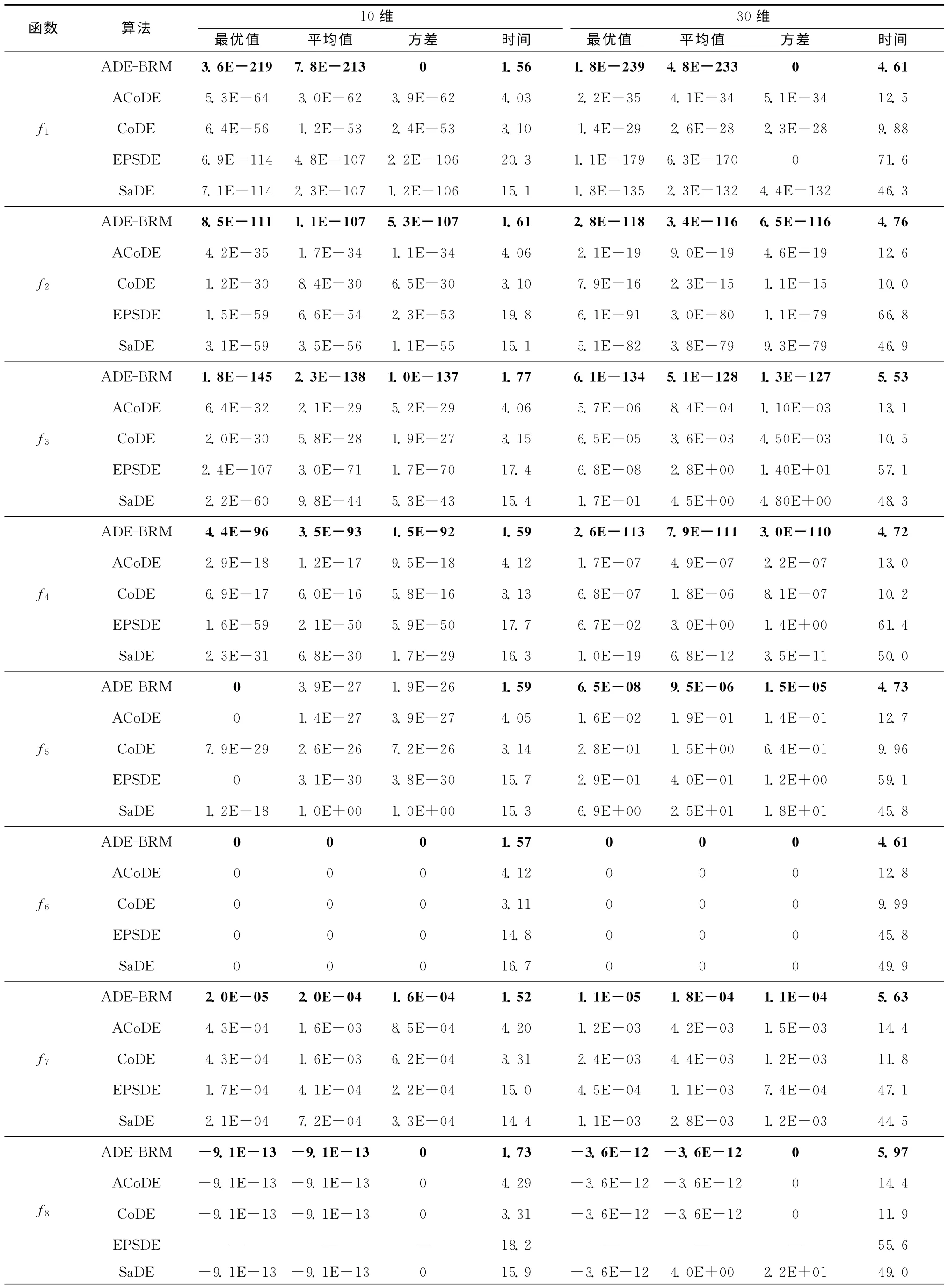
表1 不同算法仿真对比结果

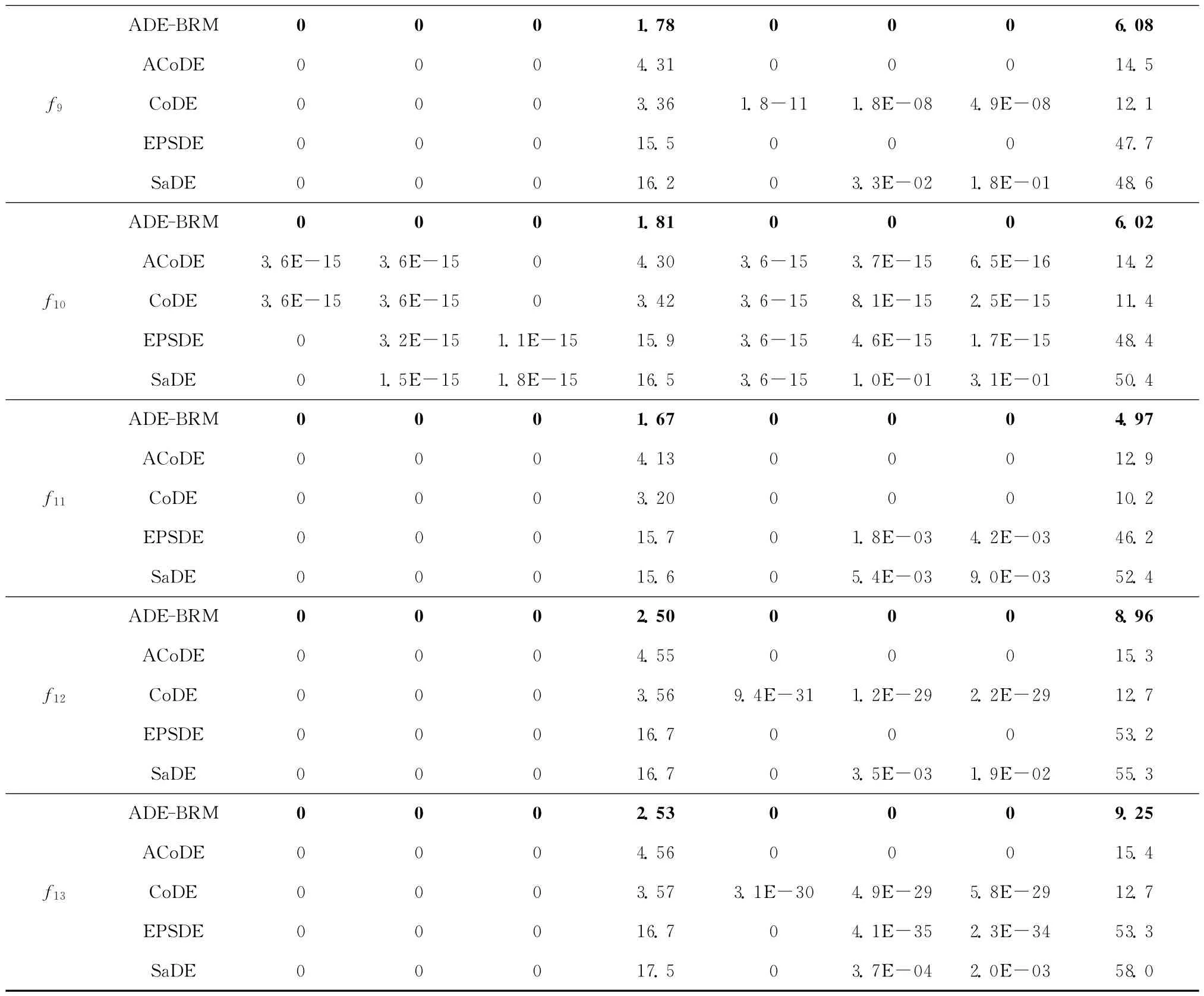
续表1

从表1可以看出，四种对比算法中，ACoDE 算法在整体性能上略高于其他三种算法，但优势并不明显。EPSDE 算法和SaDE 算法虽然在某些函数的最优值上优于ACoDE 算法和CoDE 算法，但其平均值和方差相对较差，说明算法的寻优能力较强，但稳定性不强。值得一提的是，对于相对复杂、全局最优点附近有无数局部极值点的多峰值函数f8，EPSDE算法不能正确地求解该问题，得到的解是不可行的。从整体看，四种算法的优化性能相近，均在某些方面具有局限。除函数f5和f8外，无论最优值、平均值还是方差，ADE-BRM 算法在其他11个函数上均优于其他四种算法。ADE-BRM 算法虽然能找到函数f5和f8的最优值，但在多次运行时的平均值和方差略次于ACoDE，CoDE 算法和EPS-DE算法。对于除函数f5和f8外的其他11 个函数，ADE-BRM 算法能找到包括f6和f9～f13在内的7个函数的最优值，并且方差均为0，即算法每次都能稳定地找到其最优值，说明该算法具有较强的局部搜索能力和稳定性。针对函数f1～f4和f7，ADE-BRM 算法寻优精度明显高于其他四种算法，说明该算法的收敛速度快、寻优精度高，具有更高的寻优性能。

测试函数的维数为30时，对于Rosenbrock函数f5，ADE-BRM 算法能在方向信息极少的抛物线形山谷中，尽可能地靠近全局最优点，比其他算法的精度明显高很多，说明该算法具有较强的执行能力。与其他算法相比，对于多峰值函数f9～f13，无论10维还是30维，ADE-BRM 算法均能跳出函数中存在的大量局部最优点陷阱，快速、准确、稳定地找到全局最优值，克服了由种群多样性下降引起的早熟和误收敛问题，说明该算法具有较强的全局搜索能力和跳出局部最优的能力。

从运行时间看，ADE-BRM 的运行时间最短，只有CoDE 和ACoDE 算法的一半，其余两种算法的运行时间则是前三者的5倍以上。ACoDE 算法在CoDE的基础上，采用自适应的选择变异算子，因此运行时间比CoDE 算法稍微长一些。SaDE 算法对历史信息进行学习，用以指导进化的进行，但学习过程较复杂，用时较多。ADE-BRM 无需设置F值，同时CR值的自适应学习过程简单、易于实现，因此算法运行所需的时间较少。

综上分析，ADE-BRM 算法同时具有较强的局部搜索和全局搜索能力，且算法稳定性强、运行时间短，从整体性能上优于其他四种多策略变异DE算法。

3.3 BRM 算子性能分析

为进一步分析本文所提BRM 算子的性能，在本文算法的结构框架下，选择其他四类典型的变异算子（DE／rand／1，DE／best／1，DE／current-to-rand／1，DE／current-to-best／1）进行对比实验，验证BRM算子的优越性。参数设置如下：函数维数为10，种群规模为40，学习周期为60，在最大函数调用次数为10 000D时算法停止，进行30次独立运行。表2所示为五类算子的仿真对比结果，BRM 算子不劣于其他算子的部分通过加粗部分标识。

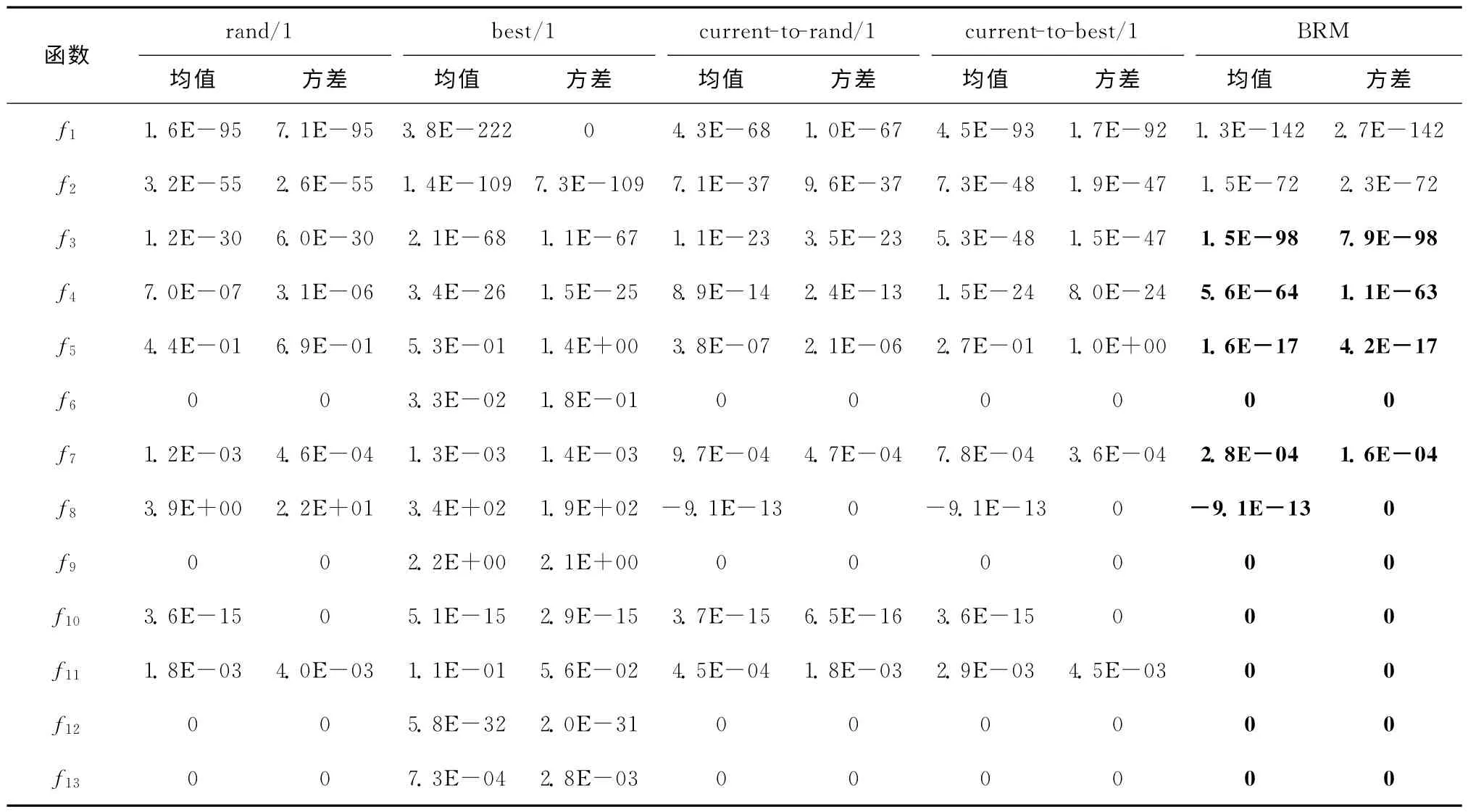
表2 不同变异算子性能比较

从表2可以看出，BRM 算子除在函数f1和f2上劣于DE／best／1 算子外，在其他11 个函数上均优于其他四种算子。函数f1和f2为单峰值函数，而DE／best／1算子的局部搜索能力强，能够很快收敛到全局最优附近，在最优个体的引导作用下，解的精度迅速提高。相对DE／best／1 算子而言，BRM算子收敛速度较慢，因此其最终解的精度低于DE／best／1算子。与此同时，由于DE／best／1算子每次均在最优个体附近搜索，很容易陷入局部最优，DE／best／1算子在解决复杂或多峰函数时性能较差，如函数f5～f13。与DE／rand／1算子在全局范围内盲目的随机搜索相比，BRM 算子能够在全局最优个体的引导下，尽可能快地收敛到全局最优，提高解的精度，这种趋势在函数f1～f5，f8和f10～f11中的表现较为明显。DE／current-to-best／1和DE／currentto-rand／1算子分别引入了最优个体和随机个体的信息，搜索过程中具有一定方向性，在解决多峰函数（如函数f8）时性能较优，虽然两算子同时具有全局寻优和局部寻优能力，但其性能均不突出。在测试的13个函数中，BRM 算子等于其他四类算子的个数分别为4，0，5和5，优于其他四类算子的个数分别为9，11，8和8，在整体性能上BRM 算子优于其他四类算子。

3.4 参数对算法性能的影响

与现有DE 算法相比，ADE-BRM 算法仅有种群规模NP和学习周期LP两个参数需要设置。为便于算法在实际中得到更好的应用，本节重点分析上述参数对算法性能的影响，同时给出参考设置。

种群规模决定了种群中个体包含的关于搜索空间信息量的大小，随着种群规模的增大，信息量逐渐增加，但在种群规模达到一定数量后，信息量的增加趋于停滞，种群规模的再次增加毫无意义。在最大函数调用次数固定的情况下，种群规模越大，进化的代数越少，算法的性能相对越差；反之，种群规模越小，进化的代数越多，但由于此时种群内个体包含的信息较少，无法给予整个种群进化提供足够有效的指导，种群进化速度缓慢，最终结果也不理想。因此，在保证种群信息充分的情况下，增加进化代数有利于提高算法性能。由于算法设计不同，各种算法种群规模的参考范围也不尽相同，Liu等［17］将种群规模设定为10D（D为优化问题的维数），Gämperle等［11］则认为种群规模在3D～8D之间最合适。除此之外，常见的参考范围还有［2D，4D］［18］，［5D，10D］［1］，［2D，40D］［15］。就ADE-BRM 算法而言，由于采用了多策略变异算子和双向随机搜索策略，相对其他算法增加了变异搜索空间，同时增加了种群的多样性，因此不需要较大的种群规模。

在其他参数固定的条件下，选取不同种群规模，进一步定量分析其对算法性能的影响。具体参数设置如下：函数维数为10，学习周期取60，在最大函数调用次数为10 000D时算法停止，进行30次独立运行。表3所示为不同种群规模时的仿真对比结果，由于函数f6和f9～f11的仿真结果均为0，没有可比性，故未列出。从表3可以看出，随着种群规模的增加，函数f1～f4解的精度逐渐降低，原因是对于单峰值函数而言，增加种群规模、减少种群进化代数后，大幅度降低了种群的开发能力。多峰函数f8，f12和f13在种群规模小于3D或大于6D时，种群均会出现误收敛的情况，类似趋势在山谷函数f5也有所体现。对于多峰函数，较小的种群容易因信息不全出现误引导而陷入局部最优，但大规模种群会因搜索范围过大而收敛较慢，因此需要选择合适的种群规模，快速准确地到达全局最优点或其附近。表3的实验结果与定性分析一致，ADE-BRM 算法一般可取种群规模为3D～6D。

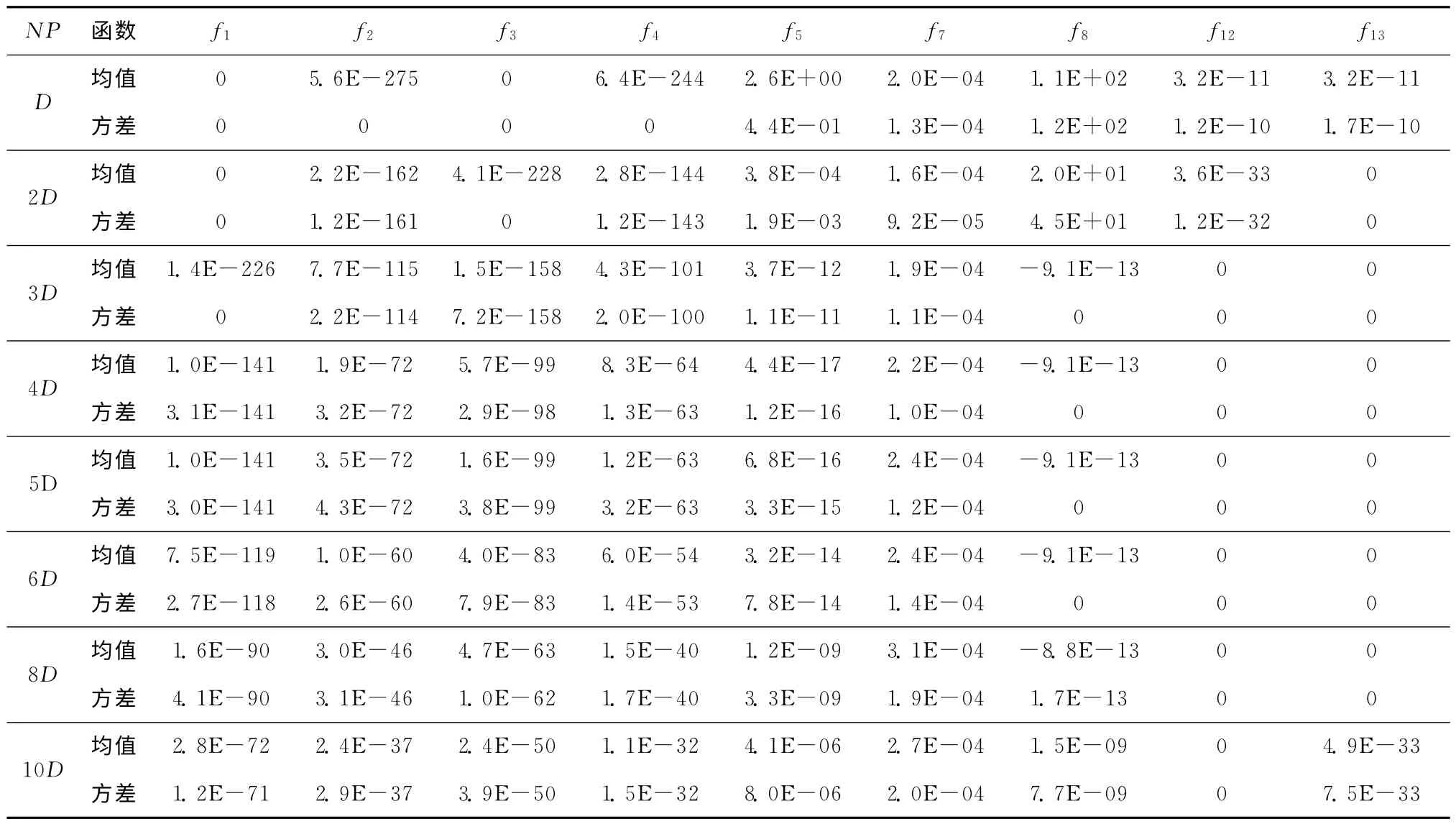
表3 种群规模NP 对算法优化性能的影响

由2.3节可知，学习周期LP表示种群对历史个体交叉过程进行学习的时间长短，即进化代数的长短。在较短的学习周期内，种群不能充分展现其进化趋势，容易造成由学习不充分引起的误引导，削弱算法的性能；反之，学习周期过长虽然能够充分了解种群的进化需要，但是由于区间选择概率的更新不及时，减缓了种群的进化。在最大函数调用次数固定的前提下，相对于种群规模，学习周期的影响较小。

在其他参数固定的情况下，选取不同大小的学习周期，进一步定量分析其对算法性能的影响。具体参数设置如下：函数维数为10，种群规模为40，在最大函数调用次数为10 000D时算法停止，进行30次独立运行。表4所示为不同学习周期时的仿真对比结果，由于函数f6和f9～f13仿真结果均为0，没有可比性，故未列出。从表4可以看出，学习周期对算法性能的整体影响较小，但对复杂的多峰函数f8的影响较为明显，在学习周期较小（＜10）或较大（＞100）时，算法均容易陷入局部极值点，出现误收敛。对于其他函数，学习周期在20～80时均值和方差的精度相对较高，因此根据以上结果可知，学习周期取20～80比较合适，通常取50即可。

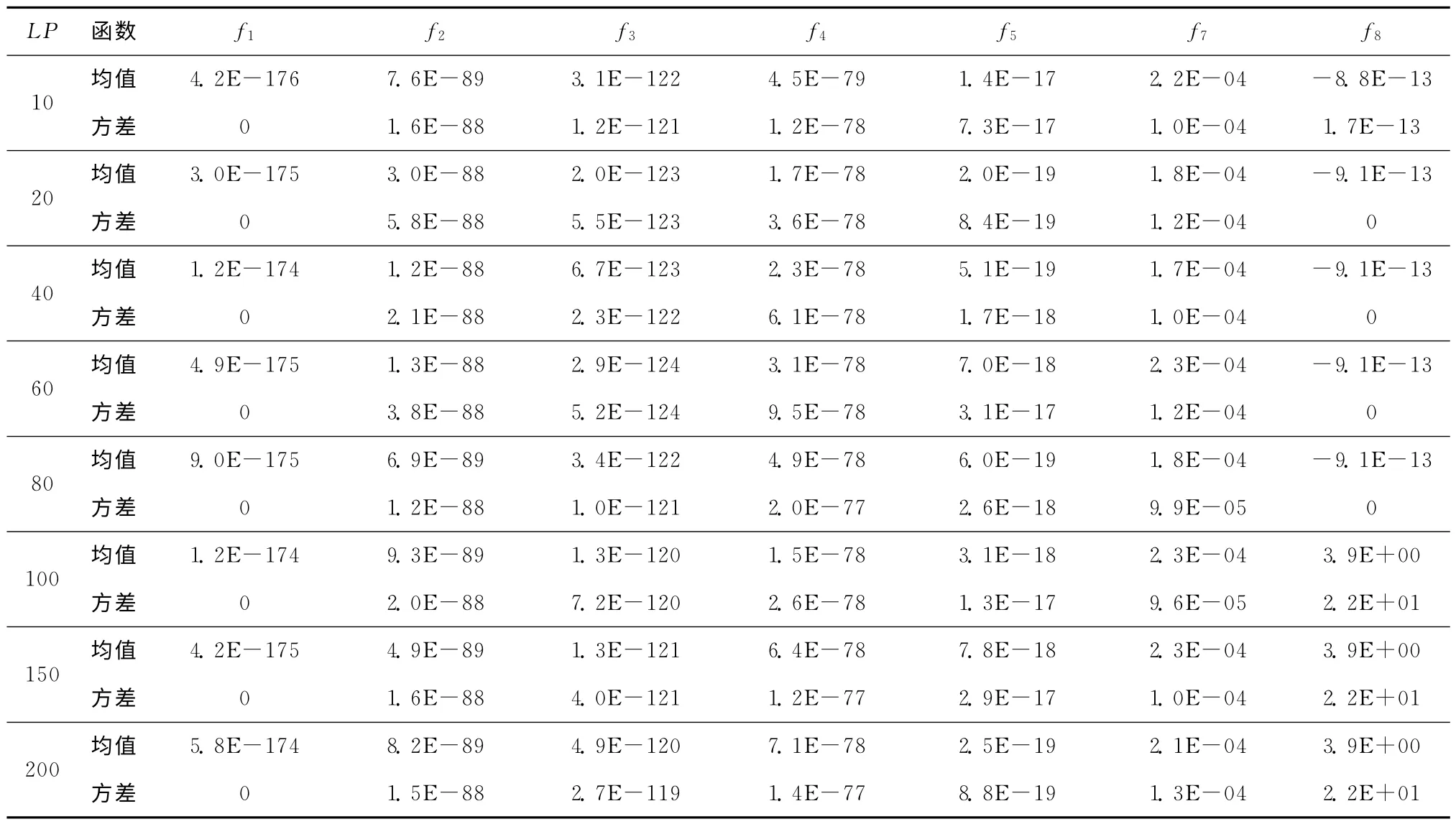
表4 学习周期LP 对算法优化性能的影响

4 结束语

差分进化算法中的单一变异算子具有局限性，同时相关参数的合理设置困难。本文从实用角度出发，提出双向随机多策略变异的自适应差分进化算法。新变异算子通过符号函数融合了现有几种典型的变异算子，使算法在保持较高种群多样性的同时，兼具较强的全局搜索能力和局部搜索能力。通过变异率的随机数化和交叉率的自适应调整策略，减少了复杂的参数选取过程，提高了算法的适用性。在标准测试函数上进行仿真对比，实验结果表明：改进算法是有效的，比其他多变异策略差分进化算法拥有更高的寻优性能和稳定性，为今后的实际工程应用提供了一条可行的途径。虽然本文算法在对比实验中显示出了相当强的优势，但其参数还只是根据实验得出的参考值，没有相关理论作指导，而实际工程相对复杂，参数选取可能对结果造成影响，因此在今后的研究中将加强算法参数设置的理论研究，同时将本文算法应用于求解实际问题。

［1］STORN R，PRICE K.Differential evolution-a simple and efficient heuristic for global optimization over continuous space［J］.Journal of Global Optimization，1997，11（4）：341-359.

［2］WANG Wanliang，WANG Lei，WANG Haiyan，et al.Dynamic Job Shop scheduling based on hybrid differential evolution algorithm［J］.Computer Integrated Manufacturing Systems，2012，18（3）：531-539（in Chinese）.［王万良，王 磊，王海燕，等.基于混合差分进化算法的作业车间动态调度［J］.计算机集成制造系统，2012，18（3）：531-539.］

［3］WANG Haiyan，ZHAO Yanwei，ZHANG Jingling，et al.Batch optimized scheduling of intermingling flow-shop based on hybrid differential evolution algorithm［J］.Computer Integrated Manufacturing Systems，2013，19（7）：1613-1625（in Chinese）.［王海燕，赵燕伟，张景玲，等.基于混合差分进化的混排Flow-shop分批优化调度［J］.计算机集成制造系统，2013，19（7）：1613-1625.］

［4］WANG Lin，CHEN Can，ZENG Yurong.Differential evolution algorithm for stochastic joint replenishment model with resource constraint［J］.Computer Integrated Manufacturing Systems，2011，17（7）：1541-1546（in Chinese）.［王 林，陈璨，曾宇容.资源约束情况下随机性联合采购模型的差分进化算法［J］.计算机集成制造系统，2011，17（7）：1541-1546.］

［5］ZHENG Jianguo，WANG Xiang.Dynamic job shop scheduling based on hybrid differential evolution algorithm［J］.Computer Integrated Manufacturing Systems，2011，17（11）：2447-2456（in Chinese）.［郑建国，王 翔.求解约束优化问题的多成员组合差分进化算法［J］.计算机集成制造系统，2011，17（11）：2447-2456.］

［6］QIN A K，HUANG V L，SUGANTHAN P N.Differential evolution algorithm with strategy adaptation for global numerical optimization［J］.IEEE Transactions on Evolution Computation，2009，13（2）：398-417.

［7］MALLIPEDDI R，SUGANTHAN P N，PAN Q K，et al.Differential evolution algorithm with ensemble of parameters and mutation strategies［J］.Applied Soft Computing，2011，11（2）：1679-1696.

［8］WANG Y，CAI Z，ZHANG Q.Differential evolution with composite trial vector generation strategies and control parameters［J］.IEEE Transactions on Evolutionary Computation，2011，15（1）：55-66.

［9］STORN R.On the usage of differential evolution for function optimization［C］／／Proceedings of the 1996Biennial Conference of the North American on Fuzzy Information Processing Society.Washington，D.C.，USA：IEEE，1996：519-523.

［10］RÖNKKÖNEN J，KUKKONEN S，PRICE K V.Real-parameter optimization with differential evolution［C］／／Proceedings of IEEE Congress on Evolutionary Computation.New Work，N.Y.，USA：IEEE，2005：506-513.

［11］GÄMPERLE R，MÜLLER S D，KOUMOUTSAKOS P.A parameter study for differential evolution［C］／／Proceedings of International Conference on Advances in Intelligent Systems，Fuzzy Systems，Evolutionary Computation.Interlaken，Switzerland：WSEAS Press，2002：293-298.

［12］NOMAN N，IBA H.Accelerating differential evolution using an adaptive local search［J］.IEEE Transaction on Evolutionary Computation，2008，12（1）：107-125.

［13］ZHANG J Q，SANDERSON A C.JADE：adaptive differential evolution with optional external archive［J］.IEEE Transactions on Evolutionary Computation，2009，13（5）：945-958.

［14］BREST J，GREINER S，BOSKOVIC B，et al.Self-adapting control parameters in differential evolution：a comparative study on numerical benchmark problems［J］.IEEE Transactions on Evolution Computation，2006，10（6）：646-657.

［15］PRICE K V，STORN R M，LAMPINEN J A.Differential evolution：apractical approach to global optimization（Natural Computing Series）［M］.Berlin，Germany：Springer-Verlag，2005.

［16］MEZURA-MONTES E，VELAZQUEZ-REYES J，COELLO COELLO C A.Modified differential evolution for constrained optimization［C］／／Proceedings of IEEE Congress on Evolutionary Computation.Washington，D.C.，USA：IEEE，2006：25-32.

［17］LIU J，LAMPINEN J.A fuzzy adaptive differential evolution algorithm［J］.Soft Computing，2005，9（6）：448-462.

［18］TEO J.Exploring dynamic self-adaptive populations in differential evolution［J］.Soft Computing，2006，10（8）：637-686.