带缓冲流水车间成组调度问题的混合微分算法
2014-12-02郑永前谢松杭钱伟俊
郑永前,谢松杭,钱伟俊
(同济大学 机械与能源工程学院,上海 201804)
0 引言
成组技术通过利用生产活动中有关事务的相似性来提高生产效率,是一种先进的生产组织理念。成组调度问题就是把成组技术的理念应用到生产调度,其基本思想为:充分利用零件在设计和加工上的相似性,将零件归类成零件组,根据生产目标优化加工顺序。成组调度问题分为组内调度和组间调度两个相关的子问题。文献[1]对成组调度问题进行了全面阐述。
本文研究的成组调度问题在流水车间的环境下,其准备时间不仅与将要加工的零件组相关,还与之前加工的零件组相关,这就是流水车间序列相关成组调度(Flow Shop sequence Dependent Group Scheduling,FSDGS)问 题。Cheng[2],Allahhverdi[3]和Zhu[4]等提供了关于这类问题的比较完整的文献综述;Scaller等[5]第一次研究了以最小化完工时间makespan为目标的FSDGS问题,提出了多种有效的启发式算法;Franca等[6]将局部搜索引入遗传算法(Genetic Algorithm,GA)和文化基因算法,以求解以最小化makespan为目标的FSDGS问题。通常,企业拥有不同的客户,每个客户的订单都需要单独配送。这种情况下,以最小化总流程时间TFT为目标比以最小化makespan为目标更有效。Garey等[7]已经证明以总流程时间为目标的多阶段流水车间调度问题是NP-hard问题,因此启发式方法是求解FSDGS问题的有效方法;Salmasi等[8]第一次以最小化总流程时间为目标构建了FSDGS问题的数学模型,采用分支定界法确定该问题的下界,使用禁忌搜索(Tabu Search,TS)算法和混合蚁群优化算法进行求解,结果表明混合蚁群算法的性能优于TS算法;Hajinejad等[9]提出一种包含个体提升邻域搜索策略的改进粒子群优化(Improved Particle Swarm Optimization,IPSO)算法,算例结果表明该算法的性能优于混合蚁群算法。上述文献都假定相邻机器之间的缓冲容量无穷大,但在现实生产环境中,由于空间和成本的限制,机器间设置的缓冲是有限的。Solimanpur等[10]将缓冲约束添加到流水车间成组调度问题,构建了组内调度和组间调度模型,并采用TS 算法求解该问题;Celano等[11]分析了序列相关准备时间对缓冲约束的影响,构建了makespan的计算公式,采用GA 求解该问题,经过与NEH(Nawaz Enscore Ham)算法[12]和TS算法的比较,证明了GA 的有效性。
综上所述,求解带缓冲的FSDGS 问题具有很强的实际应用价值,但现有文献对该问题的研究还很少。本文针对带缓冲的FSDGS 问题,以最小化总流程时间为目标建立数学模型,提出一种混合微分进化算法进行求解。
1 问题描述
1.1 问题描述及相关假设
本文研究带有限缓冲的FSDGS 问题,缓冲区采用先进先出的调度规则,当缓冲区存放的零件达到容量上限时,前一台机器加工完的零件继续留在机器上,机器停止生产,直到有零件离开缓冲区,其目标是使所有零件的完工时间之和最短。根据Pinedo[13]理论,该问题可以描述为Fm|flms,block,Splk,prmu|∑Cj。其中:Fm表示含m台机器的流水车间;flms表示成组调度问题;block 表示缓冲容量有限;Splk表示序列相关准备时间;∑Cj表示以总流程时间为评价标准。为了使问题更加明确,本文还基于以下假设:
(1)所有零件和零件组都需要按照相同的顺序在全部机器上加工。
(2)零件组在机器上的准备过程可以在组内的零件到达之前进行。
(3)零件组内的零件在机器上不需要额外的准备时间。
(4)任一零件组内的零件在加工时,不能被其他零件组内的零件打断。
1.2 数学模型
为了建立带有限缓冲FSDGS 问题的数学模型,首先定义如下变量:G为零件组数,Hg为零件组g包含的零件数(h=1,2,…,Hg),M为机器总数(m=1,2,…,M);bm表示机器m和m+1间缓冲区的容量,bm为无穷大;δ={δ(1),δ(2),…,δ(G)}表示零件组的加工顺序,δ(g)为δ中的第g个元 素,πδ(g)={πδ(g)(1),πδ(g)(2),…,πδ(g)(Hδ(g))}表示零件组δ(g)内零件的加工 顺序;Pπδ(g)(h),m表示零件πδ(g)(h)在机器m的加工时间,Rδ(g-1)δ(g),m表示机 器m加 工完零件组δ(g-1)到能够加工零件组δ(g)所需要的准备时间,Sδ(g),h,m表示零件组δ(g)内 第h个零件在机器m的开始加工时间,Dδ(g),h,m表示零件组δ(g)内第h个零件离开机器m的时间。目标是找到零件组和各零件组内零件的最优顺序,使TFT 最短。其数学模型描述如下:
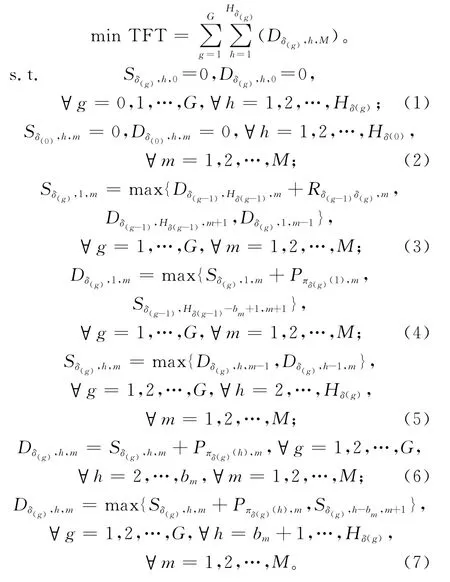
2 混合微分进化算法
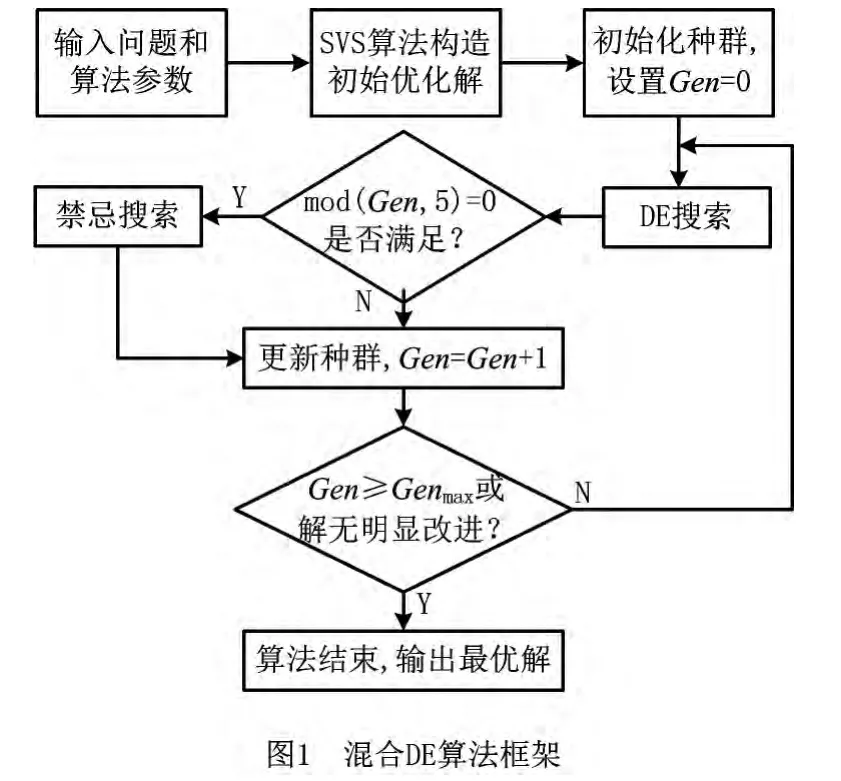
本文所提的混合微分进化算法结合了标准微分进化(Differential Evolution,DE)算法和禁忌搜索,同时对组内调度和组间调度进行求解,并利用一种有效的启发式方法(SVS算法)构造初始优化解,从而提高了求解速度,算法框架如图1所示。
2.1 SVS算法构造初始优化解
SVS算法是Solimanpur等[14]提出的一种组合启发式算法,在求解流水车间成组调度问题上,SVS算法优于其他构造算法。本文采用SVS算法构造问题的一个初始优化解,基本步骤如下:
步骤1 用NEH 算法依次产生各个零件组内零件的最优序列,记为πg,g=1,2,…,G。
步骤2 计算部分零件组序列δ1=(πi,πj)和δ2=(πj,πi)的目标函数值,其中i=1,2,…,G-1,j=i+1,…,G。
步骤3 选择一组序列,比较f(δ1)和f(δ2)的大小,若f(δ1)<f(δ2),则W(i)=W(i)+1;若f(δ1)>f(δ2),则W(j)=W(j)+1。
步骤4 判断零件组的所有两两组合是否都比较过,若是,则将零件组按W值降序排列,得到零件组的最优顺序δ;否则转步骤3。
2.2 初始化种群
对于FSDGS问题,本文用(G+1)×h的伪矩阵表示一个个体,如式(8)所示,前G行表示组内零件的顺序,最后一行表示零件组的顺序,h是零件组内最大零件数与零件组总数中的较大值。
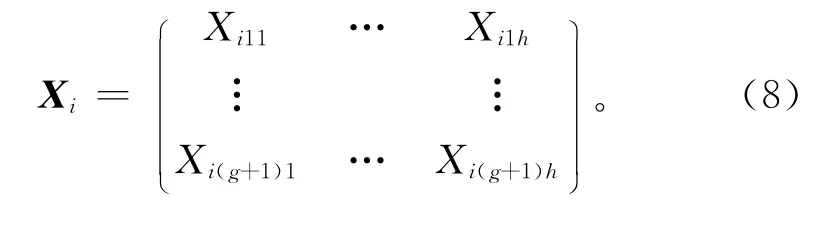
种群初始化时利用SVS算法得到的初始优化解构造其中的一个个体,种群中的其他个体根据式(9)随机生成。
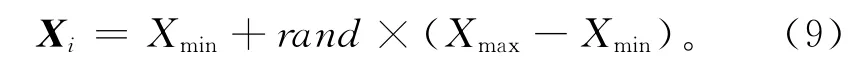
式中:i=2,3,…,PS,PS为种群数量;rand表示[0,1]的随机数;Xmax和Xmin分别为个体伪矩阵内数值的最大值和最小值。
种群中的每个个体都表示问题的一个可行解,为了计算可行解的总流程时间,采用ROV 规则将个体连续的行向量值转化成零件组和组内零件的顺序。例如,个体Xi的首个行向量Xi1=(1.06,3.98,2.77,3.14),因为第一维的值最小而排位值为1,第三维的值次之而排位值为2,所以基于ROV 规则,行向量Xi1表示的零件顺序为(1,4,2,3)。
2.3 微分进化搜索
DE算法是由Storn等[15]提出的一种新型并行搜索算法,用来求解复杂的连续优化问题,具有收敛速度快、可调参数少、鲁棒性好等优点。DE 算法包括变异、交叉和选择三种算子,可以用符号DE/X/Y/Z来区分,其中:X为确定变异个体的策略;Y为需要使用差向量的个数;Z表示交叉模式。DE算法的性能与群体规模PS、放大系数F、交叉常数CR的选择紧密相关。
2.3.1 变异算子
本文采用DE/rand-to-best/1变异算子,利用种群中任意两个个体的偏差和当前个体与最优个体的偏差生成变异个体,从而确保个体在进行变异时都能分享最佳个体的信息。
当前个体Xi(t)根据式(9)转化后得到的变异个体,记为Vi(t+1),
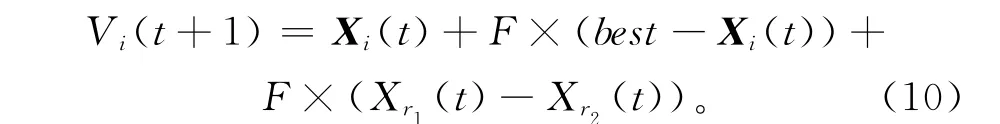
如果Vijk(t+1)<Xmin,则令Vijk(t+1)=2×Xmin-Vijk(t+1);如果Vijk(t+1)>Xmax,则令Vijk(t+1)=2×Xmax-Vijk(t+1)。
其中:r1和r2从(1,2,…,PS)随机选取;k从(1,2,…,h)中随机选取;t是当前的迭代次数;best是当代种群内的最优个体;F是放大系数,用来控制差值的放大倍数。
2.3.2 交叉算子
为增加个体的多样性,将变异个体Vi(t+1)和当前个体Xi(t)进行杂交,得到候选个体Ui(t+1)。针对个体的伪矩阵编码方式,两个个体以列为单位进行交叉,从而将个体表示成一个向量Xi=(Xi1,Xi2,…,Xih)。本文采用指数交叉算子,基本步骤如下:

2.3.3 选择算子
对候选个体Ui(t+1)进行适应度评价,根据式(11)决定是否选择新产生的个体进入下一代。
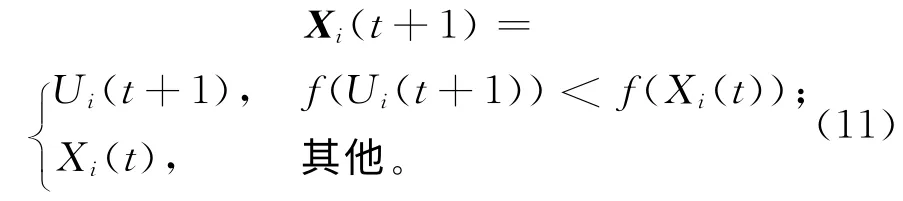
2.4 禁忌搜索
为更有效地对零件组间的邻域进行搜索,采用插入式策略,同时加入禁忌表机制,以避免发生重复移动,引导个体向更有潜力的区域进行搜索。禁忌搜索步骤如下:
步骤1 根据ROV 规则,将个体Xi的最后一行Xi,(g+1)转换成零件组的加工顺序δ。
步骤2 随机产生两个数u和v,u≠v;将δ中的第u个元素插入位置v,得到δ的一个邻域δnew。
步骤3 判断移动(u,v)是否在禁忌表中,如果存在,则转步骤2;否则转步骤4。
步骤4 如果f(δnew)<f(δ),则令δ=δnew。
步骤5 以上操作重复h×(h-1)次。
步骤6 将δ转化成Xi,(g+1),得到新个体Xi。
3 实验设计和结果分析
为验证本文所提HDE 算法的有效性,将该算法与现有文献中求解FSDGS问题最优的IPSO 算法[9]和SVS算法进行比较。选取文献[5]的实验问题作为基准问题:机器数量M=3~10,零件组数G=3~10,零件数H=10~100,零件的加工时间满足[1,10]的均匀分布。每种问题规模下生成三种序列相关的机器准备时间:短准备时间(SS)、中准备时间(MS)和长准备时间(LS),分别满足[1,20],[1,50]和[1,100]的正态分布。本文研究的FSDGS问题假设机器间的缓冲区容量都相同,设置5种缓冲区容量B为0,1,2,4和无穷大(INF)。
3.1 算法参数设置
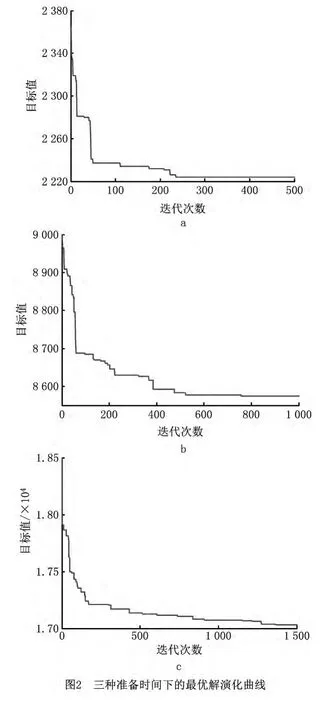
为了使本文所提算法的性能达到最优,通过数值实验确 定F,CR和PS值。F选取4种程度(0.3,0.5,0.7,0.9),CR选取3种程度(0.1,0.2,0.3),PS选取3种程度(3×G,5×G,7×G),分别对G=5,M=5和B=2的算例求解10次取平均值。考虑到三种准备时间(SS,MS,LS)对应的零件总数依次增加,问题的复杂度逐渐上升,相应的迭代次数设置为(500,1 000,1 500)。算法共运行1 080次,实验结果表明,F=0.7,CR=0.2,PS=7×G时算法的性能最优。准备时间SS,MS,LS下最优解的迭代曲线如图2所示,可见在给定迭代次数内算法能收敛到最优解。
3.2 算法性能比较
为了保证比较的公平性,所提算法和IPSO 算法的种群数量和最大迭代次数相同,三种算法均在CPU Core i3-2370@ 2.4 GHz 的计算机上,用MATLAB 7.9进行编码。表1所示为B=1和B=2时30种问题规模下三种算法得到的总流程时间TFT百分比 偏差,其中ΔF1=100×(TFTSVSTFTIPSO)/TFTSVS,ΔF2=100 ×(TFTSVS-TFTHDE)/TFTSVS,ΔF3=100 ×(TFTIPSO-TFTHDE)/TFTIPSO。从表中可以看出:在30个问题中:B=1时,本文算法得到的解都优于SVS算法,3个问题的解差于IPSO 算法,26个问题的解更优,与SVS算法相比,IPSO 和本文算法的TFT平均值改进了4.13%,4.96%,本文算法比IPSO 算法改进了0.85%;B=2时,本文算法得到的解都优于SVS算法,5个问题的解差于IPSO 算法,22个问题的解更优,与SVS算法相比,IPSO 和本文算法的TFT平均值改进了4.23%,4.99%,本文算法比IPSO 算法改进了0.78%。总体来说,在求解质量上,本文算法优于SVS算法和IPSO 算法。
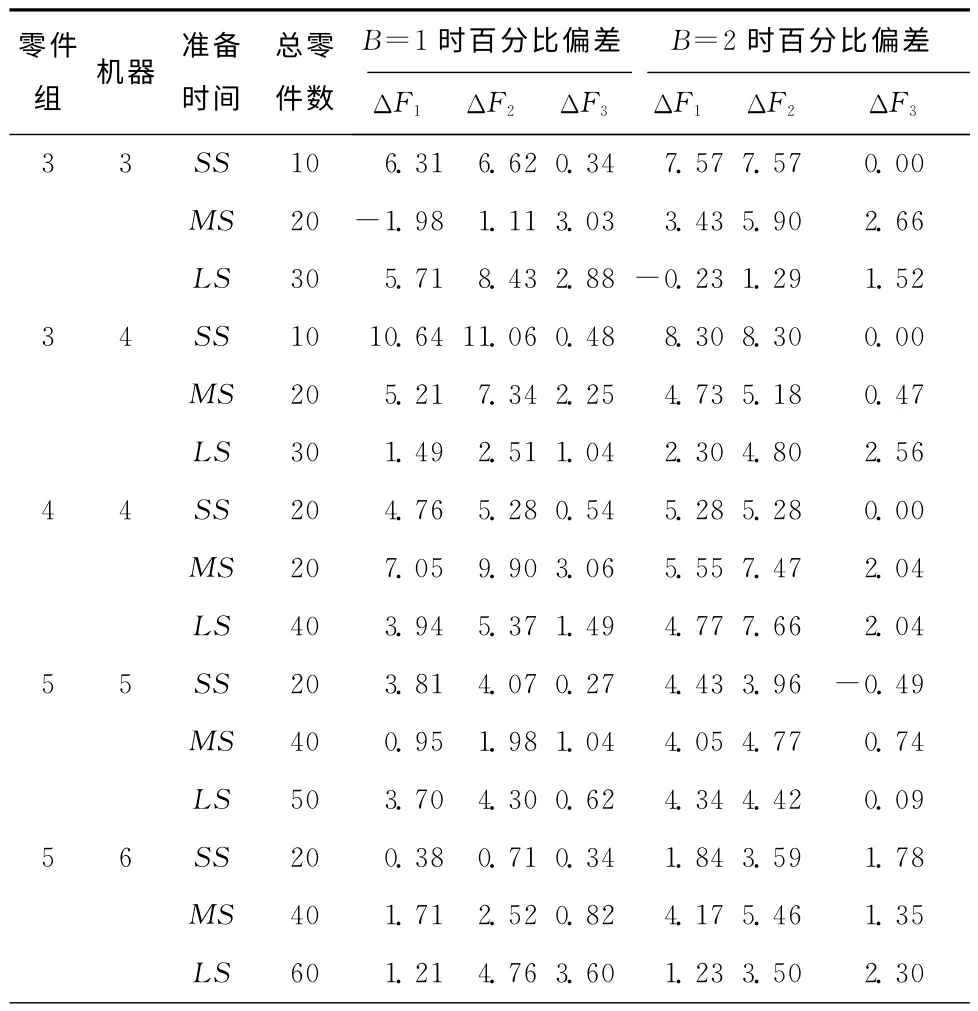
表1 各算法得到的TFT 百分比偏差
3.3 缓冲容量对总流程时间的影响
采用本文提出的混合微分算法求解不同规模问题,对实验结果进行分析后得出缓冲容量对总流程时间的影响。表2所示为不同缓冲容量下TFT的百分比偏 差,Δ1=100×(TFTB=0-TFLB=1)/TFTB=0,Δ2=100 ×(TFTB=1-TFLB=2)/TFTB=1,Δ3=100 ×(TFTB=2-TFLB=4)/TFTB=2,Δ4=100×(TFTB=4-TFLB=INF)/TFTB=4。从表中可以看出:在30个问题中,从B=0到B=1,所有问题得到的解都得到了改进,TFT平均值降低了7.45%;从B=1到B=2,28个问题的解得到改进,TFT平均值降低了1.91%;从B=2到B=4,24 个问题的解得到改进,TFT平均值降低0.99%;从B=4到B=INF,19个问题的解得到改进,TFT平均值只降低了0.5%。
从对比结果看,问题缓冲容量较小时,增加缓冲能显著降低TFT,随着缓冲容量的增加,下降幅度逐渐减小,当下降幅度趋于0时,即达到了问题的临界缓冲点。

表2 不同缓冲容量下的TFT 百分比偏差
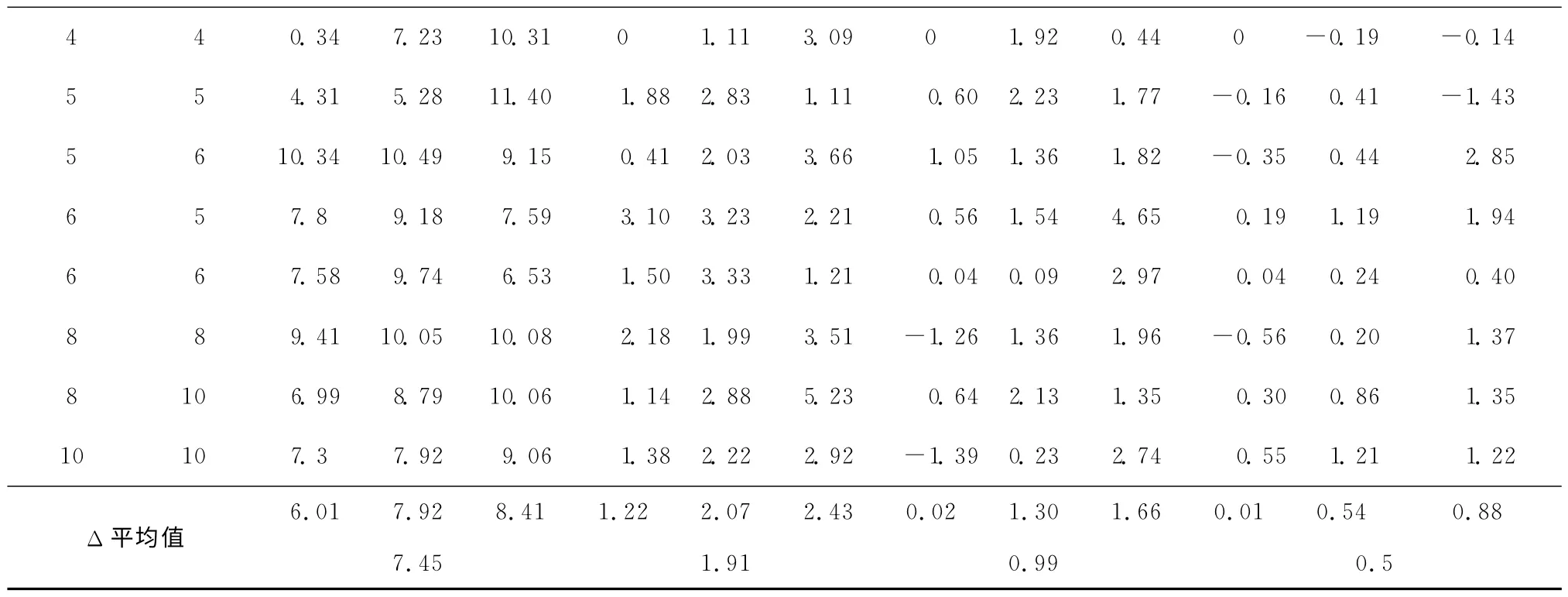
续表2
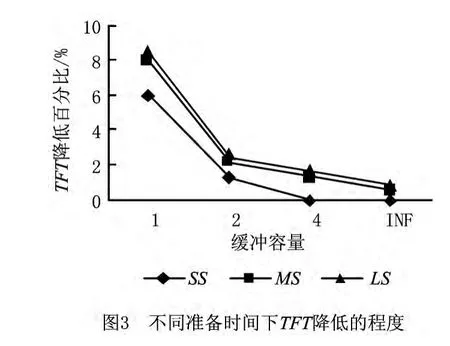
图3中,三条曲线分别表示三种准备时间下得到的总流程时间降低程度与缓冲容量的关系。从图中可以看出,在SS下,B=4时改进水平趋于0,说明B=4为临界缓冲点;在MS和LS下,B=4时改进水平分别为1.3%和1.66%,表明机器的准备时间越长,临界缓冲就越大,需要设置更多的缓冲,使总流程时间达到最短。
4 结束语
本文针对带缓冲约束的FSDGS 问题,以总流程时间最短为目标建立了数学模型,设计了一种将微分进化算法和禁忌搜索相结合的混合微分进化算法。该算法利用微分进化的并行性搜索确定各组内零件顺序,应用禁忌搜索寻找最优的零件组顺序。为了提高求解速度和精度,利用构造算法产生问题初始优化解,并通过数值实验确定算法的最优参数。选取IPSO 算法和SVS算法为比较对象,通过不同规模的算例测试,证明了本文所提算法能有效地解决带缓冲约束的FSDGS问题。
[1]WEMMERLOV U,HYER N L.Cellular manufacturing in the U.S.industry:a survey of users[J].International Journal of Production Research,1989,27(9):1511-1530.
[2]CHENG T,GUPTA J,WANG G.A review of flowshop scheduling research with setups[J].Production and Operations Management,2011,24(3):257-268.
[3]ALLAHVERDI A,CHENG T,KOVALYOV M.A survey of scheduling problems with setup times or costs[J].European Journal of Operations Research,2008,187(3):985-1032.
[4]ZHU X,WILHELM W E.Scheduling and lot sizing with sequence-dependent setups:a literature review[J].IIE Transactions,2006,38(11):987-1007.
[5]SCHALLER J E,GUPTA J,VAKHARIA A.Scheduling a flow line manufacturing cell with sequence dependent family setup time[J].European Journal of Operations Research,2000,125(2):314-339.
[6]FRANCA P M,GUPTA J,MENDES P M.Evolutionary algorithms for scheduling a flowshop manufacturing cell with sequence dependent family setups[J].Computers and Industrial Engineering,2005,48(3):491-506.
[7]GAREY M D,JOHNSON D S,SETHI R.The complexity of flowshop and jobshop scheduling[J].Mathematics of Operations Research,1976,1(2):117-129.
[8]SALMASI N,LOGENDRAN R.Total flow time minimization in a flowshop sequence-dependent group scheduling problem[J].Computers &Operations Research,2010,37(1):199-212.
[9]HAJINEJAD D,SALMASI N,MOKHTARI R.A fast hybrid partical swarm optimization algorithm for flow shop sequence dependent group scheduling problem[J].Scientia Iranica E,2011,18(3):199-212.
[10]SOLIMANPUR M,ELMI A.A tabu search approach for group scheduling in buffer-constrained flow shop cells[J].International Journal of Computer Integrated Manufactur-ing,2011,24(3):257-268.
[11]CELANO G,COSTA A,FICHERA S.Constrained scheduling of the inspection activities on semiconductor wafers grouped in families with sequence-dependent set-up times[J].International Journal of Advanced Manufacturing Technology,2010,46(5/6/7/8):695-705.
[12]NAWAZ M,ENSCORE E E J,HAM I.A heuristic algorithm for the m-machine,n-job flow shop sequencing problem[J].Omega,1983,11(1):91-95.
[13]PINEDO M.Scheduling theory,algorithms,and systems[M].3rd ed.Englewood Cliffs,N.J.,USA:Prentice Hall,2008.
[14]SOLIMANPUR M,VRAT P,SHANKAR R.A heuristic to minimize makespan of cell scheduling problem[J].International Journal of Production Economics,2004,88(3):231-241.
[15]STORN R,PRICE K.Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):341-359.
