NURBS插补中的速度规划与参数计算

王允森，杨东升，刘荫忠，孙一兰

（1.中国科学院 沈阳计算技术研究所，辽宁 沈阳 110168；2.中国科学院大学，北京 100049）

0 引言

对于复杂曲面、曲线的加工，传统数控系统采用离散化的微小直线段或圆弧段逼近曲线。这种方法容易造成进给速度轮廓的不连续和波动，破坏工件表面的光滑性，而且产生的大量程序增加了计算机辅助设计（Computer Aided Design，CAD）／计算机辅助制造（Computer Aided Manufacturing，CAM）和计算机数控系统（Computer Numerical Control，CNC）之间的通信负担，影响了插补的实时性［1］。非均匀有理B 样条（Non-Uniform Rational BSpline，NURBS）曲线是国际标准化组织规定的CAD／CAM 数据交换标准，在CAD 系统中应用广泛，但是在CNC系统中的发展相对滞后，只有一些高档数控系统如SIEMENS、FANUC 等实现了NURBS曲线插补功能。

近年来，国内外学者针对样条曲线插补做了大量研究并取得了较大的进展。Bedi等首先提出均匀参数插补算法［2］，将插补参数增量视为常数进行实时插补。该算法首次实现了样条曲线的直接插补，但是因不能控制进给速度而应用不多。Shipitalni和Yang等分别采用泰勒一阶、二阶展开式计算插补参数［3-4］，实现了恒定进给速度插补，提高了计算精度，减小了速度波动；孙海洋等提出用牛顿迭代法计算插补参数的算法［5］，进一步提高了计算精度。但是上述算法没有考虑加减速过程中的速度变化要求，难以保证插补精度，且误差难以控制。Yeh等提出一种自适应的参数曲线插补算法［6］，该算法根据加工精度的要求自动调节进给速度，使得弦高误差控制在精度允许的范围内。但是该算法没有考虑机床的实际加减速能力，加工过程中过大的加速度和加加速度会对机床造成很大冲击，从而影响加工质量［7］。Nam 等提出加速度控制算法［8］，将加速度约束考虑在内，减小了数控机床在加工过程中的震动，但是这种方法的实现比较复杂。

本文在上述研究的基础上，对NURBS插补中的速度规划和参数计算进行了研究。通过采用简化的五段S曲线加减速控制算法进行速度规划，保证了速度和加速度的连续变化，并实现了加加速度的有界变化。插补参数的计算采用抛物线插值和牛顿迭代法结合的方法，可以减小速度波动，进一步提高加工质量。仿真实验表明，本文所提的插补算法能够得到连续的速度和加速度曲线，并且能够将实时插补的速度波动控制在理想范围内，从而实现机床的平稳运行，满足高速度、高质量加工的要求。

1 NURBS曲线插补

一条k次的NURBS曲线定义为

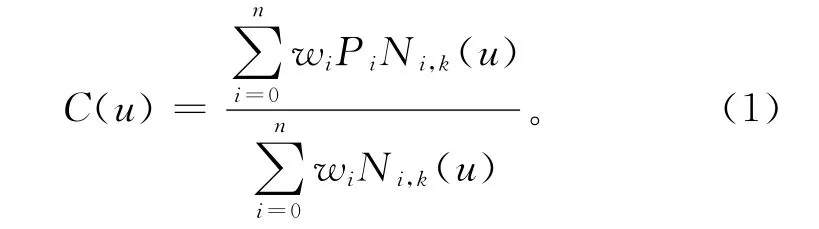
式中：u为NURBS曲线的参数；Pi为控制点；wi为每个控制点对应的权重，首末权重w0，wn＞0，其余权重wi≥0；Ni，k（u）为k次NURBS基函数，由节点矢量U=（ui，ui+1，…，ui+k）确 定，并满足Cox-de Boor递推关系式

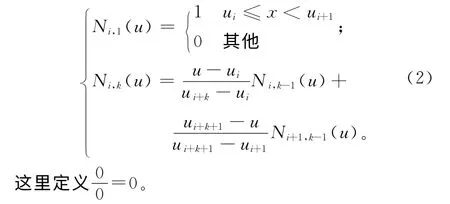
NURBS曲线插补时，通常用弦长来逼近弧长。但是因为样条曲线的弧长和参数之间的关系为非线性，所以实时插补时往往不能获得插补参数的精确值，只能获得近似值，从而使理想进给速度与实际进给速度之间存在差异，即进给速度波动，进而导致实际进给速度偏离加减速控制规划的速度，影响运动的平稳性，甚至使加速度和加加速度超出限制范围，造成运动冲击，最终影响工件表面的加工质量［9］。速度波动的大小可用速度波动率δi衡量：

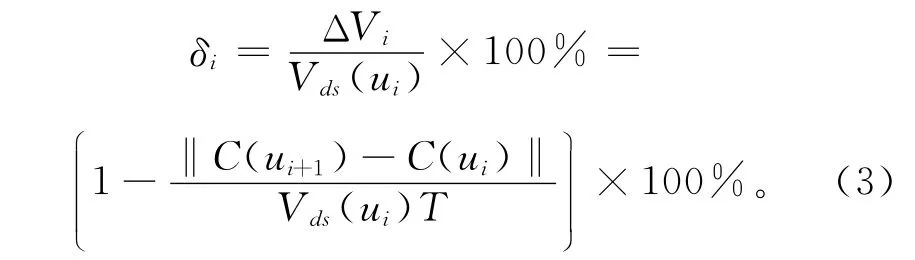
式中：Vds（ui）为插补参数ui处的理想进给速度，ΔV为理想进给速度与实际进给速度的差值，T为插补周期。

2 速度规划算法

2.1 五段S曲线速度方程推导

五段S曲线加减速控制算法将速度规划分为加加速段、减加速段、匀速段、加减速段和减减速段五个阶段。以减速过程为例，其速度曲线为二次抛物线，加速度曲线为线性直线，加加速度曲线为常数直线。减速过程的速度曲线、加速度曲线、加加速度曲线如图1所示。

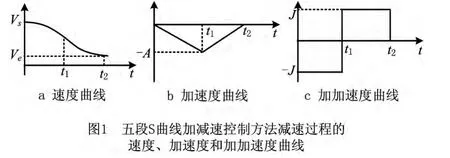
从图1可以看出，整个减速过程可以分成加减速段和减减速段两段。设加减速段的速度曲线方程为

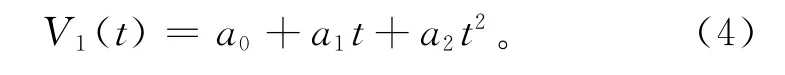
对速度方程分别求一阶导数和二阶导数，可以得到加速度和加加速度方程：

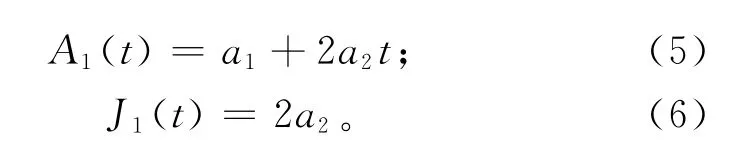
假设减速过程的开始时刻为0，起始速度为Vs，终止速度为Ve，最大加速度为A，最大加加速度为J，加减速阶段的时间为0～t1，减减速阶段时间为t1～t2。

从图1中可以看出，当t=0时，速度为Vs，加速度为0，加加速度为-J，即V（0）=Vs，A（0）=0，J（t）=-J。由以上信息可得a0=Vs，a1=0，a2=-0.5J。

因此加减速阶段的速度方程曲线为

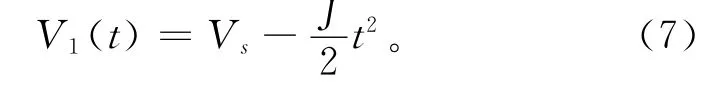
当t=t1时，A1（t1）=-Jt=-A，有

同理可得减减速阶段的速度方程为

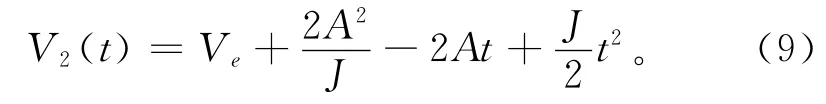
由于整条速度曲线是连续的，有

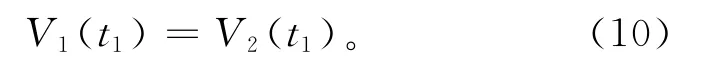
将式（7）～式（9）代入式（10），可得

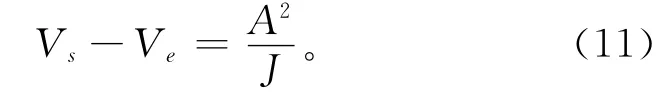
设减速阶段速度的变化量为ΔV，即ΔV=Ve-Vs，当｜ΔV｜=时，能够达到机床加工的最大加速度和最大加加速。若

则加速度无法达到最大值A，设此时达到的最大加速度为Al，由式（11）可得

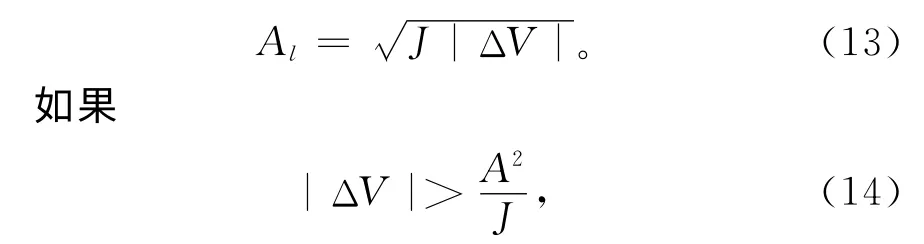
则最大加加速度无法达到J，设此时最大加加速度为Jl，由式（11）可得

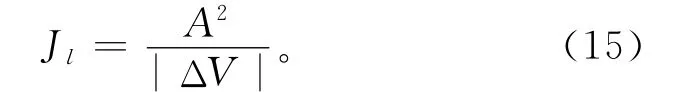
因此，在计算减速段的速度方程时，首先根据速度变化量ΔV与的大小关系，计算减速阶段能达到的最大加速度和最大加加速度，然后代入式（7）和式（9），可以分别获得加减速段和减减速段的方程，加速过程的加加速段和减加速段方程可以用相同的方法计算。

2.2 快速预插补

对加工轨迹进行快速预插补的目的是为了找出加工轨迹中的速率敏感点，从而进行有效地速度规划。

快速预插补阶段需要记录插补路径的长度，并根据加工精度的要求记录减速开始点和速度极小值点，然后计算该极小值点需要的减速距离。

在NURBS曲线插补时，通常用圆弧近似的方法计算弦高误差与进给速度及曲率间的关系，如图2所示。图中：Ei为弦高误差，ρi为曲率半径，Li为进给步长。设插补时参数u=ui处的进给速度为V（ui）。

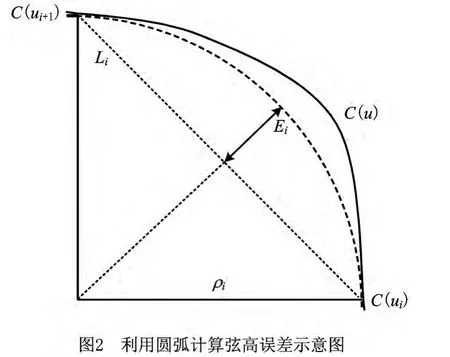
通过几何关系可以求出

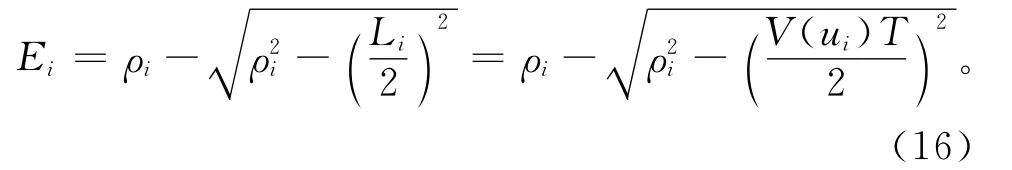
根据式（16），若假设加工所要求的最大弦高误差为ER，则该误差约束下的速度

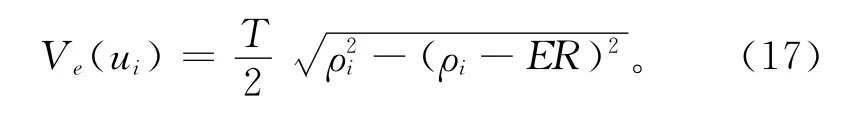
若设定加工时的最大速度为F，则插补时的进给速度

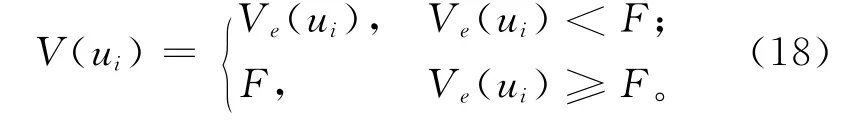
预处理阶段只是统计实时插补时所需要的数据，因此对插补参数的精度要求不是很高，可以用一阶泰勒展开法来计算，公式如下：

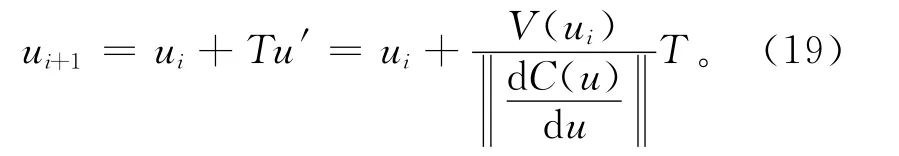
假设在参数u=um处，按加工精度要求，加工的速度开始递减，此时速度为Vm，而在u=un处速度达到极小值Vn，此时加工路径长度为ln。

为了确定该减速段的速度方程，首先计算减速过程的最大加速度A和最大加加速度J能否达到，即比较Vm-Vn和的大小，若满足Vm-Vn=，则最大加速度A和最大加加速度能够达到；若Vm，则加速度无法达到最大值A，按照式（13）计算实际能达到的最大加速度Al；若Vm-Vn，则最大加加速度无法达到J，按照式（15）计算实际能达到的最大加加速度Jl。

根据加减速段的速度方程式（7），积分后可以求出加减速段的位移曲线方程

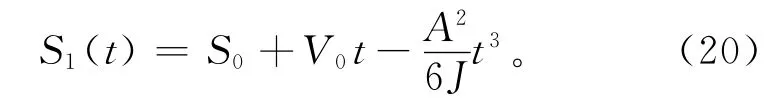
因此加减速段的位移量为

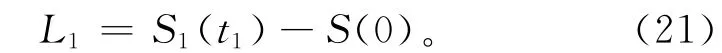
同理，可以获得减减速段的位移量为L2，故该减速段的位移量

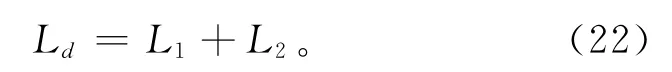
在得到减速距离Ld后，向前依次寻找插补参数，直至找到参数uk，其对应的路径lk满足

比较um和uk的大小，若um＜uk，则记录um为实际减速段的起点参数，否则记录uk的值为减速起点参数。

快速预插补结束时，得到一个加减速段数组ACC＿DEC［］数组中每个数据的结构如下：

3 实时插补

3.1 实时进给速度的计算

预处理阶段已经获得加速段或减速段的始末插补参数、速度方程等信息，实时插补时则要根据这些信息计算实时插补的进给速度，然后计算插补参数，代入样条曲线方程后求出各个轴的移动量。确定进给速度的主要思想如下：

比较当前的插补参数ui、当前加减速段的起始参数ACC＿DEC［x］.Us 和结束参数ACC＿DEC［x］.Ue的大小，若ui＜ACC＿DEC＿DATA［x］.Us，则保持刀具做匀速运动，若ACC＿DEC［x］.Us＜ui＜ACC＿DEC［x］.Ue，则根据快速预插补阶段求出的速度方程计算进给速度，若ui-1＜ACC＿DEC［x］.Ue，ui＞ACC＿DEC［x］.Ue，则将x加1，并保持刀具做匀速运动。

在减速时，有可能出现ui＜ACC＿DEC［x］.Ue，而V（ui）≤ACC＿DEC［x］.Ve，即速度提前减为最小值的情况，为了避免频繁的加减速控制，应使其保持当前速度做匀速运动。

3.2 插补参数实时计算

NURBS曲线插补时，泰勒系列展开法是最常用的插补参数计算方法。为了有效减小截断误差，降低速度波动，必须尽可能用进给弦长逼近实际弧长，即采用高阶泰勒展开，但是用这种方法进行计算非常复杂，难以满足插补的实时性。这里采用牛顿迭代法结合抛物线法计算插补参数。

3.2.1 迭代式的确定

设当前的插补参数为ui，下一个插补参数ui+1=ξ。根据速度波动率的定义（式（3））创建的构造函数为

因此问题转化为求ξ=ξ＊，使得

设ξk和ξk-1是F（ξ）=0的两个近似根，分别计算F（ξk）和F（ξk-1）的值。令

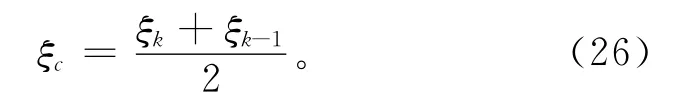
将ξc代入F（ξ）中计算出F（ξc），并利用（ξk-1，F（ξk-1）），（ξk，F（ξk））和（ξc，F（ξc））三个点构建F（ξ）的抛物插值多项式P（ξ），

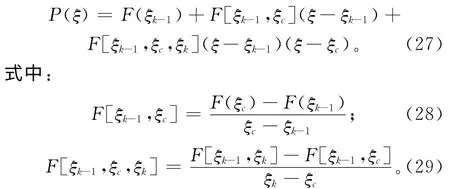
将式（28）和式（29）代入式（27）并求一阶导数：

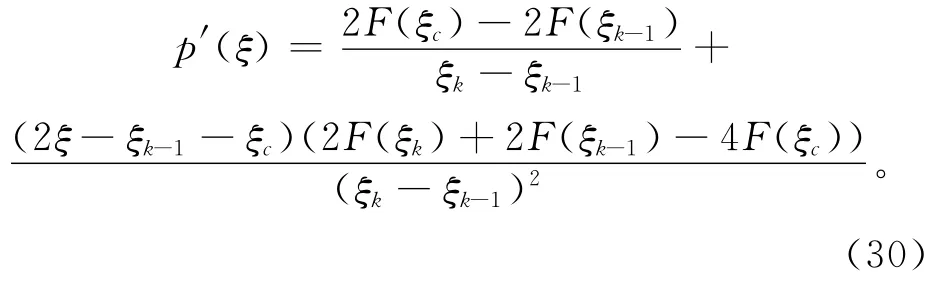
将式（26）代入式（30），可得

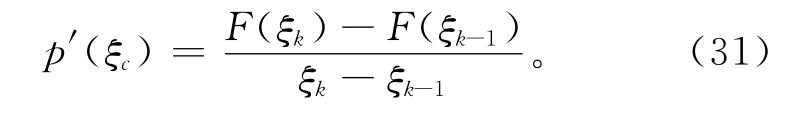
从而可以写出曲线P（ξ）过（ξc，F（ξc））点的切线方程，以这条切线方程与ξ轴交点的横坐标作为ξ＊新的迭代值，即采用牛顿迭代法计算ξk+1，

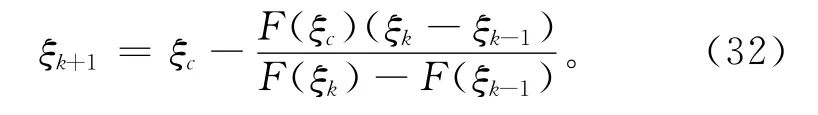
因为选择的NURBS曲线为三次，C（u）具有连续的二阶导数，所以F（ξ）同样具有连续的二阶导数，只要迭代初值选取恰当，迭代式（32）就能满足收敛性［10］，且使收敛阶达到2。

3.2.2 迭代初值的计算

应用牛顿迭代（式（32））计算插补参数时需要两个迭代初值。为减小计算量，这里采用线性递推法获得两个参数初值：

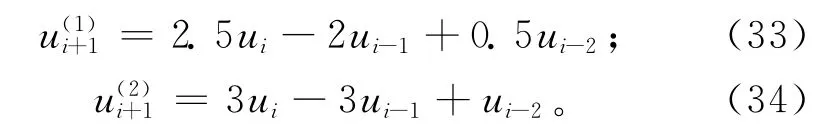
递推式（33）为二阶线性阿当姆斯递推方程，推导过程如下：

二阶阿当姆斯预测方程为

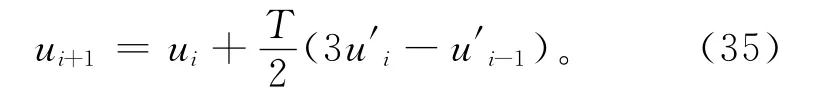
用差分方程代替求导运算，有

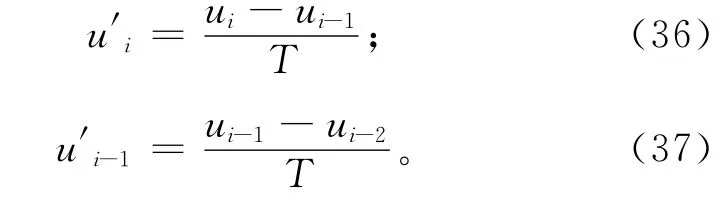
将式（36）和式（37）代入式（35），化简可得到二阶线性递推方程（33）。

递推式（34）为二阶线性泰勒递推方程，推导过程如下：

二阶泰勒展开式为

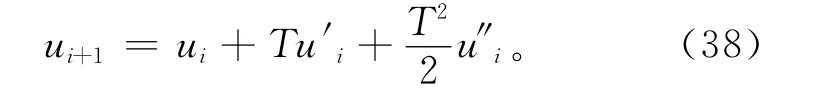
用差分方程代替求导运算，有

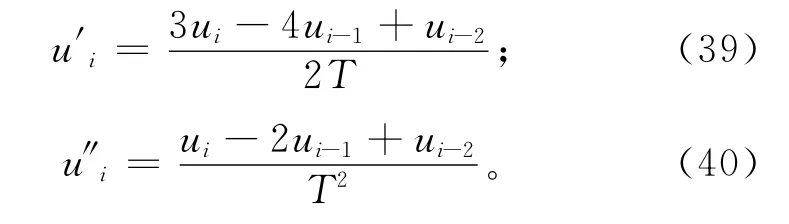
将式（39）和式（40）代入式（38）进行化简，可得二阶泰勒递推式（34）。

从式（33）和式（34）中可以看出，在估计下一个插补参数时，仅需用到前面三步插补参数的线性运算。初始的三个插补参数的初值可以用二阶阿当姆斯预测方程（式（35））和二阶泰勒展开式（式（38））计算。

3.2.3 迭代终止条件

采用迭代法计算插补参数的目的是为了减小速度波动，提高加工质量，因此设定迭代终止条件为

式中：δi+1为当前计算出的插补参数ui+1对应的速度波动率，Δ为速度波动率的上限。另外，考虑到插补的实时性，设定算法的最大迭代次数K。

4 仿真分析

为了验证上述NURBS 曲线插补算法的有效性，选择二维NURBS曲线进行仿真，如图3所示，曲线参数如表1所示。仿真时的编程速度F=0.2 m／s，插补周期T=0.002s，最大加速度A=0.005 m／s2，最大加加速度J=0.000 4m／s3，允许的最大弦高误差Emax=0.000 5mm，最大允许速度波动率Δ=10-6%，最大迭代次数K=5。

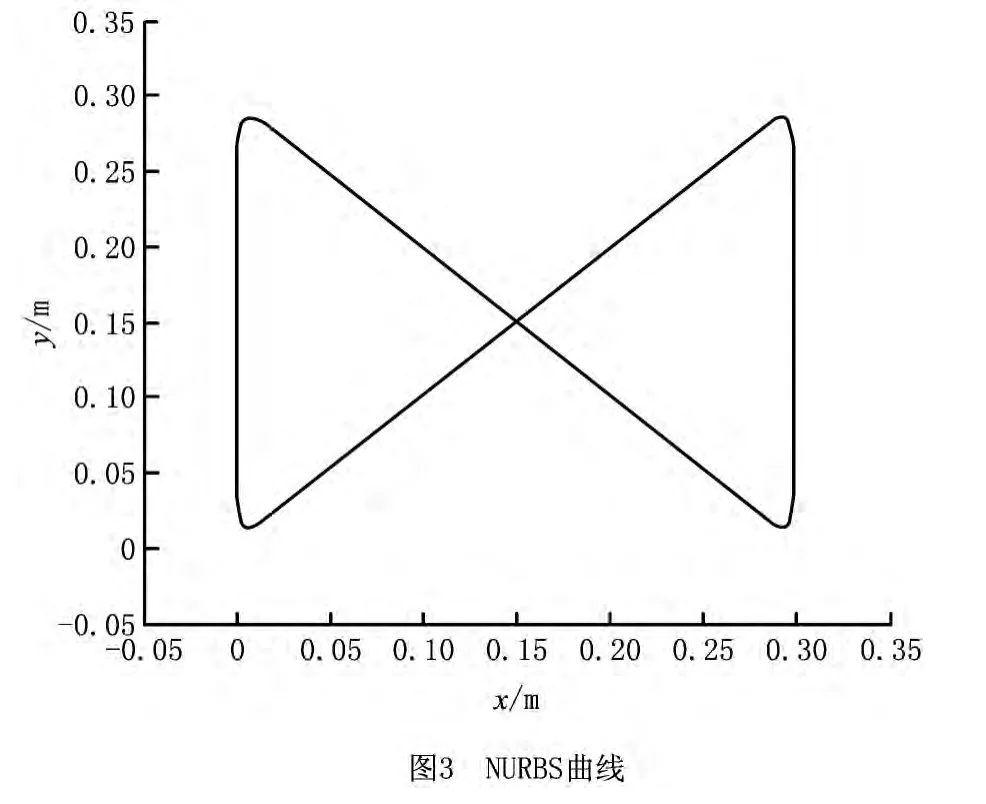
表1 NURBS曲线参数列表

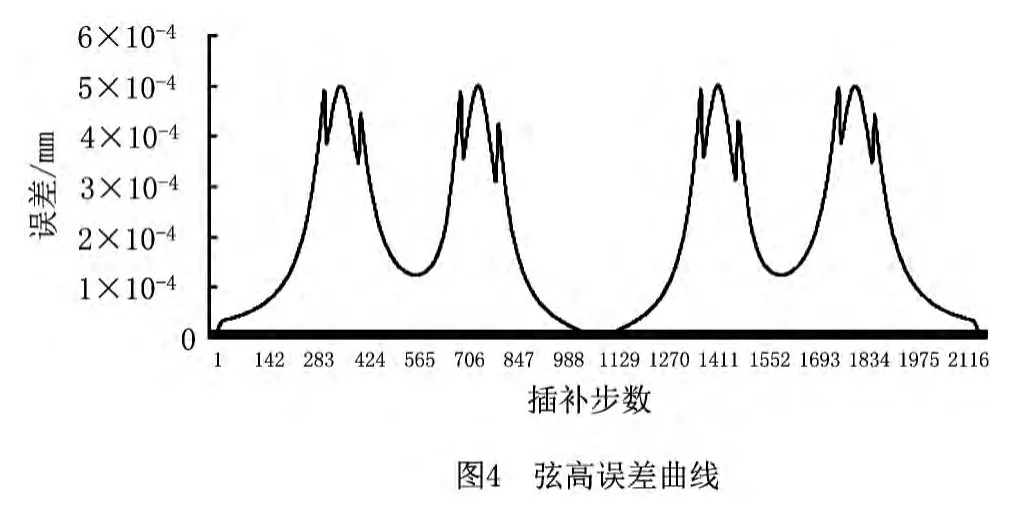
仿真得到的误差曲线如图4所示。可以看出，本文所提算法满足了加工的精度要求，即所有插补点的弦高误差都控制在Emax以内。

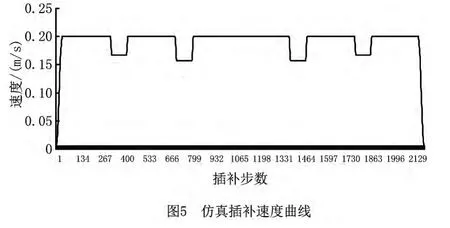
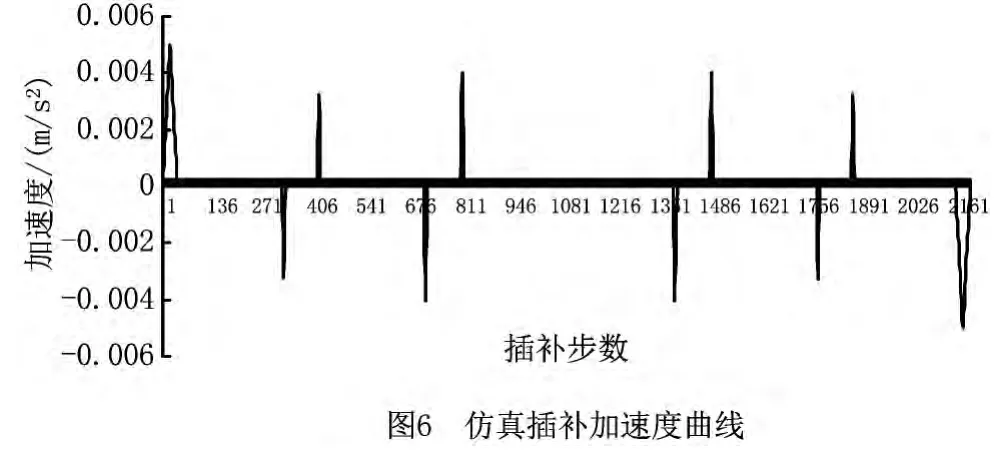
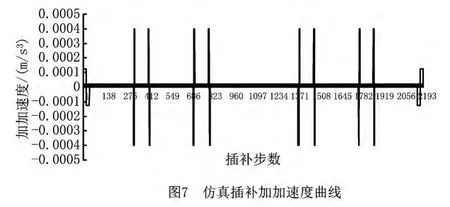
仿真实验得到的的速度曲线、加速度曲线及加加速度曲线分别如图5～图7所示。从图中可以看出，在仿真插补过程中，进给速度限制在编程速度F内，加速度和加加速度也都限制在最大加速度A和最大加加速度J的范围内。

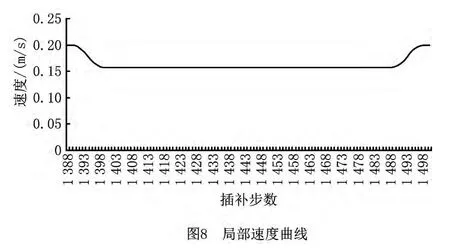
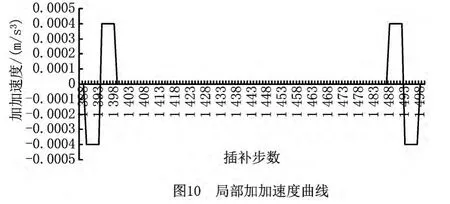
为了说明本文算法中速度规划方法的特点，选取局部速度曲线及相应的加速度曲线和加加速度曲线进行分析，如图8～图10所示。该速度曲线包含减速段、匀速段和加速段。从图中可以看出，整条速度曲线实现了平滑变化，而加速度在减速段和加速段实现了连续变化，加加速度则在-J和J内实现了有界变化。从图9可以看出，在加速和减速时没有达到最大加速度A。

为了验证应用抛物线插值结合牛顿迭代法计算插补参数的可行性和有效性，仿真实验进一步以常用的一阶泰勒展开法、二阶泰勒展开法作对比，测试本文所提算法在减小速度波动方面的表现。采用5段S曲线加减速算法，对图3所示的NURBS曲线进行仿真加工，分别采用本文算法和一阶、二阶泰勒展开法计算插补参数，并按式（3）计算对应的速度波动率，得到的对比结果如图11～图13及表2所示。图11～图13分别为应用一阶泰勒展开法、二阶泰勒展开法和本文所提算法计算插补参数时的速度波动率变化曲线，表2指出了各种方法的速度波动率的最大值、逆向最大值，以及所有点的速度波动率的绝对值的平均值。

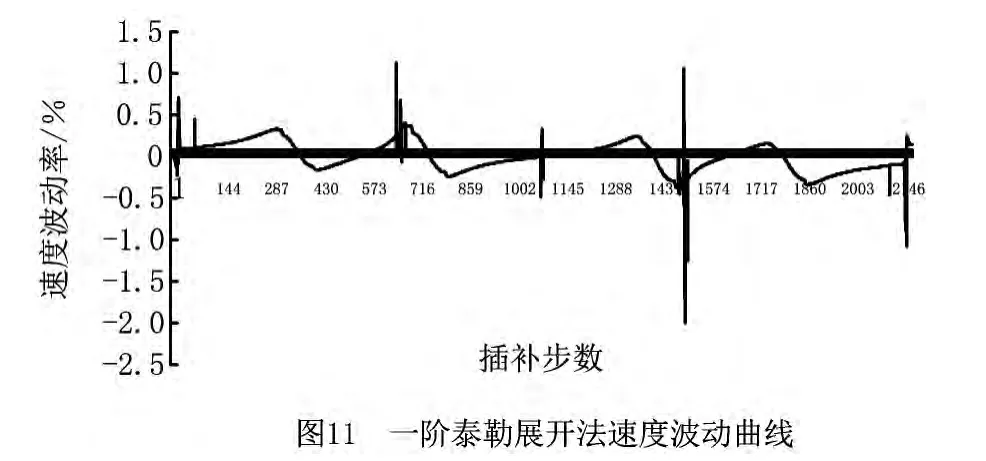
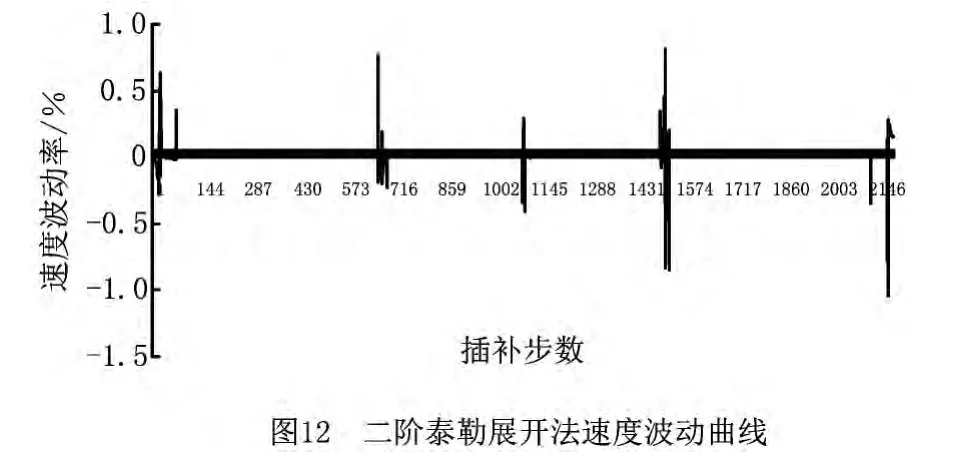
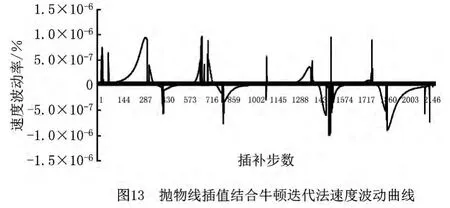
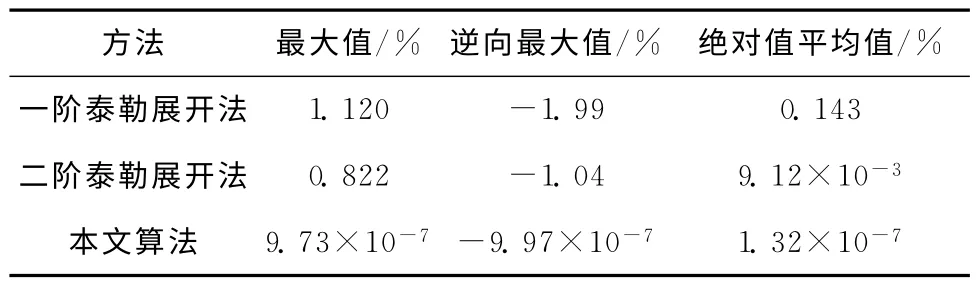
表2 本文算法与一阶、二阶泰勒展开法速度波动率的比较 %

通过对比实验结果可以看出，一阶泰勒展开法的速度波动率较高，最大的速度波动率达到1.99%；二阶泰勒方法较一阶泰勒展开法有一定改进，速度波动率的平均值较一阶泰勒展开法降低了两个数量级，但最大的速度波动率仍然超过1%；而本文提出的应用抛物线插值结合牛顿迭代法计算插补参数的方法，所有插补点的速度波动率已经控制在10-6%范围内，且平均速度波动率达到10-7%量级，比一阶泰勒展开法降低106倍，比二阶泰勒展开法降低了104倍。对图3仿真加工的插补数一共为2 196步，统计的全部迭代次数为2 535次，即绝大多数插补参数仅需迭代一次，速度波动率就能达到10-6%量级，并且本文所提方法没有用到NURBS曲线的求导运算，参数初值的预测采用简单线性递推方程计算，进一步减小了计算开销。由此可知本文所提方法是可行和有效的。

5 结束语

本文对NURBS曲线插补中的速度规划和参数计算方法进行了研究。其中，速度规划部分采用简化的5段S曲线加减速控制方法，保证了高速运行过程中速度和加速度的连续变化，使机床运行平稳，避免对机床产生大的冲击；而参数计算部分则采用抛物线插值结合牛顿迭代法来实时计算插补参数，减小了速度波动，进一步减小了机床震颤。仿真实验表明，该算法能够得到连续的速度和加速度曲线，缓解高速加工过程中产生的振动和过冲，减小机床震颤，并且能够将进给速度波动控制在理想范围。

［1］TSEHAW Y，RANGA N.A parametric interpolator with confined chord errors，acceleration and deceleration for NC machining ［J］.Computer-Aided Design，2003，35（13）：1249-1259.

［2］BEDI S，ALI I，QUAN N.Advanced interpolation techniques for CNC machines［J］.Journal of Engineering for Industry，1993，115（3）：329-336.

［3］SHPITALNI M，KOREN Y，LO C C.Real-time curve interpolators［J］.Computer-Aided Design，1994，26（11）：832-838.

［4］YANG D C H，KONG T.Parametric interpolator versus linear interpolator for precision CNC machining［J］.Computer-Aided Design，1994，26（3）：225-234.

［5］SUN Haiyang，FAN Dapeng，LI Ling.A novel method for real-time CNC curved path interpolation calculating［J］.Journal of National University of Defense Technology，2008，30（3）：122-127（in Chinese）.［孙海洋，范大鹏，李 玲.一种参数曲线实时数控插补计算新方法［J］.国防科技大学学报，2008，30（3）：122-127.］

［6］YEH S S，HSU P L.Adaptive-feedrate interpolation for parametric curves with a confined chord error［J］.Computer-Aided Design，2002，34（3）：229-237.

［7］LUO Jun，WANG Jun，LIU Xueming，et al.Adaptive NURBS interpolation algorithm with look-ahead function based on S-shape acceleration／deceleration［J］.Computer Integrated Manufacturing Systems，2013，19（1）：55-60（in Chinese）.［罗钧，汪 俊，刘学明，等.基于S 型加减速的自适应前瞻NURBS曲线插补算法［J］.计算机集成制造系统，2013，19（1）：55-60.］

［8］NAM S H，YANG M Y.A study on a generalized parametric interpolator with real-time jerk-limited acceleration［J］.Computer-Aided Design，2004，36（1）：27-36.

［9］LUO Fuyuan，YOU Youpeng，YIN Juan.Research on stability and improvement of Taylor-expansion-based approach for NURBS curve interpolation［J］.China Mechanical Engineering，2012，23（4）：383-388（in Chinese）.［罗福源，游有鹏，尹涓.NURBS曲线泰勒展开插补法的平稳性与改进研究［J］.中国机械工程，2012，23（4）：383-388.］

［10］LEI Xiuhong，CHEN Lanping.A new method for solving the nonlinear equation［J］.Journal of Capital Normal University，2001，22（2）：22-24（in Chinese）.［雷秀红，陈兰平.求解非线性方程的一种新方法［J］.首都师范大学学报，2001，22（2）：22-24.］