网络交通流宏观基本图:回顾与前瞻*
2014-12-02马万经廖大彬
马万经 廖大彬
(同济大学道路与交通工程教育部重点实验室 上海 201804)
0 引 言
长期以来,交通政策预期效果评估,网络演化分析以及状态预测等,依赖于交通需求预测模型.因而模型的准确性和可靠性对评价结果至关重要.为提高这些预测分析模型性能,诸多方法被提出,模型所需数据的粒度和复杂度也逐渐上升.从20世纪50 年代提出的“四步骤”模型(four-step model),发展到70 年代的 非集计模型(disaggregate demand model)和网络均衡模型(network equilibrium),再到90年代的动态仿真模型(dynamic simulation).理论上,计算机可以基于这些模型对交通网络进行分级预测分析.但正如Daganzo[1]指出,如下问题的存在使得这些模型的应用存在缺陷:(1)模型需要太多输入参数,比如动态OD(origin-destination,OD);(2)行者的选择行为是一个不可预测的博弈过程;(3)饱和网络的行为非常复杂.与这些模型不同,宏观基本图(macroscopic fundamental diagram,MFD)直接利用网络检测数据,从宏观角度对网络进行集计分析,进而对网络进行监控和管理.由于这一方法避免了前述诸多问题,其提出后即引起了广泛关注.本文试图对相关研究成果进行总结和分析,并梳理出具有潜在价值的研究问题和方向.推动MFD 理论研究及其在交通网络分析和拥挤管理等多方面的应用.
1 MFD 的总体研究脉络
2007年Daganzo和Geroliminis[2]通过日本横滨的数据发现,单个检测器数据的流量占有率关系具有很大的离散型,见图1.然而,将整个网络的所有检测器的流量和占有率集聚后,可以形成一个离散度很小的曲线,见图2,并基于此提出了反应网络交通流状态的宏观基本图概念.

图1 单个检测器流量与占有率关系

图2 多检测器流量与占有率/密度关系
MFD 反映了整个网络交通量与网络运行水平的普遍关系,其不仅仅描述了网络流量与占有率的关系,也反映出网络内车辆数和流出网络车辆数之间的关系,以及车辆运行里程与运营时间之间的关系等.通过对MFD 的分析,Daganzo发现其基本曲线形式为抛物线,但在实际的分析中常简化为三角形或梯形[3].
MFD 引起交通网络分析、管理和控制等多领域的广泛关注.相关学者主要围绕其基本性质、影响因素及应用方向等方面展开研究.主要研究脉络见图3.
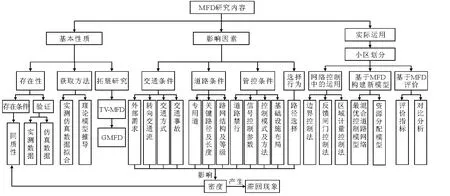
图3 MFD 总体研究脉络
2 MFD 基本性质研究
MFD 被揭示之后,首先开展其基本性质的研究,主要集中在其存在性、获取方法及拓展研究等几个方面,见图4.这些研究逐步从不同角度揭示了MFD 的特征和影响因素,为MFD 在交通状态分析、管理和控制等各领域的研究和应用奠定了基础.

图4 MFD 基本性质研究框架
Daganzo在提出MFD 时指出,一个网络只有在其内部交通状态处于“同质性”时,即整个小区要么全部处于拥挤状态要么全部不处于拥挤状态,才存在离散度低的MFD.随后,大量学者就各种原因导致的网络“非同质性”对MFD 的影响展开了研究,探索了不同影响因素对MFD 离散度的影响.
继日本横滨发现MFD 的存在后,MFD 的存在性也在不同的地方通过不同的数据得到验证.Gonzales等[4]通过仿真方法验证了内罗毕路网MFD 的存在,姬杨蓓蓓等[5]通过仿真研究发现阿姆斯特丹的城市路网同样存在MFD;Gao等[6]运用斯德哥尔摩的交通数据(包含检测器数据和出租车数据)发现在该城市存在MFD;He等[7]利用检测器数据验证了北京三环线构建的交通网络存在MFD.
MFD 除可以通过仿真和实际数据获取,也可以通过解析模型构筑.Leclercq等[8]提出依据路径的拓扑结构,以及变分理论来获取MFD,该方法克服了以往获取MFD 的规则条件,对现实许多“非同质性”的网络也适用;Geroliminis等[9]对变分理论做了一定的扩展与改进,模型中主要考虑了整个网络的最大通行能力以及最大密度;Xie等[10]考虑了小汽车交通和公共交通,提出了两种获取城市干道网络MFD 的方法.方法一是结合内部公共交通运行与移动瓶颈理论来获取MFD;方法二则在方法一基础上考虑了外部公共交通.Daganzo等[11]利用旧金山网络数据提出了一个精确的分析表达式,来表达MFD.Courbon等[12]对比分析了获取MFD 的三种方法:分析法、基于路径的方法、检测器法,并通过仿真对上述方法进行了评价.分析法具有最严格的约束,但在仿真中需要大量参数标定;检测器法虽然很容易获取MFD,但有时所得到的结果具有比较大的离散性,而且需要布设大量检测器;基于路径的方法可以获取MFD 但车辆路径的获取难度较大.由此可见,虽然MFD 可以通过实际检测器获取,但对于一个大的城市路网,可能会出现有效检测器数量不足以获取整个城市的MFD,解析方法则可以在更少的数据条件下,获取小区的近似MFD 表达式.
在MFD 图形的基础上,Knoop等[13]提出的双变量(密度、网络中总交通量)宏观基本图(TVMFD),对处于“同质性”及“非同质性”条件下的网络均适用.在此基础上,提出了表示流量与平均密度,以及密度不均衡性之间的关系的GMFD,能很好地解释MFD 的“滞回现象”[14].
3 MFD 影响因素研究
在MFD 基本性质和存在性研究的基础上,对MFD 的影响因素的研究也逐渐深入.可归结为以下4个方面:交通条件、道路条件、管控条件以及选择行为,基本研究框架见图5.

图5 MFD 影响因素研究框架
对MFD 影响因素的研究,最先引起大家注意的是Geroliminis发现的“滞回现象”[15-16].所谓“滞回现象”就是流量与占有率比例关系图为封闭曲线,而不是线性曲线.Geroliminis发现引起这种现象的主要原因为网络密度的不均匀性,以及数据量不足.由此揭开了对MFD 影响因素研究的序幕.总体而言,不同因素,最终都是通过对网络密度的影响,进而对MFD 产生各方面的影响.
3.1 不同交通条件对MFD 的影响
许多学者在研究过程中同样观测到了“滞回现象”,并进行了解析.He通过对北京城市快速路网MFD 分析,发现由于匝道上车辆的频繁变道使得匝道上密度分布不均匀进而产生了该现象.许菲菲等[17]发现在外部需求变化大时,会出现上述现象.朱琳等[18]通过研究外部需求在不同总量和时变比例下,对MFD 的影响,发现在初期,总量和时变影响较小,到了后期两者对MFD影响的差距很大.Mahmassani等[19]在城市网络处于过饱和条件下通过对MFD“滞回现象”的研究,提出了一种可以描述整个网络处于非同质性下的新模型,从而克服了MFD 的不足.
在研究有关转向交通流对MFD 的影响时,Geroliminis等[20]发现,交叉口处左转交通流的存在减小了MFD 的最大值.Boyaci通过变分理论研究转向交通流对MFD 的影响也得到了同样的结论.
Geroliminis等[21]通过研究巴塞罗那城市混合交通网络下的宏观交通流特征,探索了不同比例公交及私人小汽车出行对MFD 离散度的影响,发现小汽车出行比例越大,曲线离散度越大.Zheng等[22]探讨了不同交通方式的空间分布及各种模式所占比例对MFD 的影响,发现随着公交专用道在整个城市所占比例的提升,整个小区的内部车辆数将不会达到MFD 的最大值.
王玉等[23]通过仿真研究了交通事故、占路施工、恶劣天气对MFD 的影响,发现交通事故以及占道施工发生的位置对曲线形状影响不显著,而恶劣天气这种影响全局的事件对整个路网的影响更显著.
3.2 不同道路条件对MFD 的影响
不同道路条件对MFD 影响研究,主要集中在专用道的性质、路网中关键路径,以及路网结构等级3个方面.
许菲菲等研究了公交专用道以及关键路径对MFD 的影响,发现设置公交专用道会在一定程度上降低路网的通行能力,进而降低了MFD 最大值,并确定了路网中对MFD 有决定性作用的关键路段.Buisson等[24]探讨了城市网络、穿越城市的高速网络与环城高速网络对MFD 的影响.研究发现MFD 的形状与道路网络的形状有很大关系,高速网络不存在MFD,因此不同类型路网的混合最终会到导致无法得到网络的MFD.朱琳等通过对比西三环路网及其子路网MFD,发现路网结构越均匀,各路段交通状态差异越小,路网整体性能越高.
3.3 不同管控条件对MFD 的影响
在对MFD 影响因素的研究中,对不同管理及控制措施和参数的研究最为突出.
许菲菲发现道路禁行不仅会降低路网服务水平,也会改变MFD 的形状.马莹莹等[25]则通过仿真发现信号周期对MFD 形状几乎没有影响.Jin等[26]通过元胞传输模型发现在自由流状态下,网络稳定时MFD 很稳定,而间断流状态下信号控制使得网络交通流不稳定,进而影响到MFD 形状.
Qian等[27]将2种不同的管理方式(匝道控制和增减车道)运用到网络中,对于匝道控制法,采取控制前后的MFD 差不多,匝道控制会加快高速路网拥挤的消散,但使城市网络拥堵情况加剧.Gonzales等[28]通过将无信号控制的环岛改为信号控制交叉口,发现改变前后MFD 形状发生变化.Zhang运用元胞自动机模型对比分析了城市干道路网3 种不同自适应交通控制模式(SCATS-L,SCATS-F,SOTL)对MFD 的影响,发现由于SOTL 控制方式主要是为了使网络的交通均匀分布,因此采用该模式时网络宏观交通状态最好.Buisson研究发现在一个城市网络中,检测器距信号控制位置的距离不仅会改变MFD的形状,也使得数据的离散度增加.Courbon 发现,检测器距离较远时,该位置检测到的数据都是车辆处于自由流状态,因此对MFD 初始部分形状没有影响,而当检测器位置距离信号控制位置很近时,由于其检测到的都是拥堵状态的数据,对饱和状态下的MFD 形状没有影响.
3.4 不同选择行为对MFD 的影响
除了有关交通条件、道路条件以及管控条件以外,有关不同选择行为对MFD 的影响研究也取得了一定的成果.
朱琳研究发现,不同路径选择方式影响了路网MFD 的形状,改变了路网阻塞密度.Leclercq研究了不同路径选择模型(Wardrop模型、Logit模型、系统最优模型)对MFD 的影响,发现无论网络是否处于处于稳定状态下,Wardrop模型下的网络MFD 是一致的.Zhao等[29]同样通过仿真研究了实时的交通出行信息以及驾驶员路径选择行为对MFD 的影响,研究发现,不同路径选择通过网络密度的影响,进而对MFD 最大值产生影响,消息预知比例越高,最后MFD 最大值会相应增大.
4 MFD 在交通网络分析与控制等领域的应用研究
随着对MFD 基本性质及影响因素的深入研究,人们对如何将MFD 运用到实际中去产生了极大的兴趣.在运用MFD 时,首先需要解决的是基于MFD 的网络交通小区划分的问题.在此问题上不少学者也做了许多研究.随后一系列有关MFD 运用的研究逐步开展起来.基本研究框架见图6.

图6 MFD 实际运用研究框架
基于MFD 的交通小区划分方法的研究被许多人关注.其中最典型的研究当属于Ji等面向MFD 的小区划分问题研究.其依据在一个特定时间内的拥挤特征来划分整个网络,并最后拓展到对小区的动态划分问题上[30-31].Haddad等[32]在研究2个小区之间基于MFD 的最优控制问题,提出了基于MFD 的边界控制模型,并在此基础上形成了一个新的模型用以对小区的划分.随后,李刚奇等[33]在宏观交通流理论基础上研究了小区划分方法,提出了对子区划分进行控制的小区划分标准.马莹莹等[34]也利用谱方法以相邻交叉口的关联性作为划分依据,对交通小区进行划分.虽然各种划分方法考虑的因素不太相同,但最终目的都是为了使得划分后的小区具有交通流的同质性.
4.1 MFD 在网络控制中的运用
随着对MFD 研究的不断深入,对宏观基本图的运用也有了比较初步的认识.Daganzo 和Geroliminis论述了MFD 可以通过控制交通需求来提高道路可达性,并以此来确定城市的驶出车辆占车辆总数的比例.随后,其研究了通过边界控制策略来控制2个小区,使得各小区内交通量能均衡的分布在保证小区驶出流量最大时的总流量位置处[35-37].Haddad等以2 个交通小区为研究对象,提出了一种最优边界控制方法.最后以城市不同拥挤程度下MFD 的稳定性作为分析指标,证明该方法比反馈调节算法更优[38-39].王福建等[40]总结了对趋于拥堵的路网区域实施边界控制策略思想,并提出了基于MFD 性质的一些城市管理的措施.Mehdi等[41-42]基于网络MFD 研究了的反馈闸门控制方法.通过仿真对干尼亚州网络进行闸门控制,取得了很好的效果.Yoshii等[43]将MFD 运用到过饱和网络控制中,提出了一种区域计量控制方法.文章通过对阪神快速路网络的仿真研究,验证了该方法的有效性.
4.2 MFD 在构建新模型方面的运用
将MFD 运用到网络交通控制中已经取得了很多成果,对于MFD 在构建新模型方面的运用方面也展开了许多研究
Ramezani等[44]探讨了由高速路网络与城市网络共同形成的网络的宏观交通流关系,采用元胞传输模型以网络总延误最小为目标,构建了混合道路网络的最优控制模型.Daganzo等[45]研究了将宏观交通流模型与经济学模型相结合,进而使得对私人小汽车及公用交通的合理均衡的利用,这对决定在何时何地将有限的资源给何种运输方式有很大的作用.
4.3 MFD 作为评价手段的运用
将MFD作为评价手段的研究主要围绕以下二方面展开:一方面将MFD 的稳定性作为评价指标;另一方面则与MFD得到的结果作对比分析.
Knoop等[46]运用MFD 分析了交通控制与传统采用大量数据复杂算法之间优劣,研究发现运用详细的复杂算法控制效果比使用MFD 效果要好,但基于MFD 同样可以进行有效的控制.Lin等[47]提出了2个用于评价网络控制模型的指标并通过分析网络MFD 的稳定性说明以上两个指标是合适的.
Zheng等[48]结合城市路网交通拥挤宏观模型以及基于智能体的模拟器研究了拥挤收费策略.通过苏黎世城市路网首先证明了运用智能体模拟器获得的结果与通过MFD 所得到的结果的一致性,随后在基于MFD 控制下提出了一种动态拥挤收费策略.Horiguchi等[49]将MFD 公式化,然后通过公式化后的MFD 来表达反映网络目前的运营情况的两个变量:流动性指标和突出性指标.Gayah等[50]利用网络的MFD 及浮动车的数据实时预测网络交通密度.该方法主要优势在于所需的实际数据少,计算简单.虽然在非拥挤情况下预测结果不准,但是在拥挤情况下预测结果令人信服.
5 总体分析
MFD 提出至今,相关研究已取得许多成就,对MFD 的认识也逐步清晰.相关学者主要围绕其基本性质、影响因素及运用方向等方面展开研究.综合相关成果,尚有如下问题值得进一步深入探索.
1)MFD 影响因素的定量分析模型的一般形式及其参数确定方法 相关研究大多基于具体网络数据进行了MFD 影响因素的分析及其存在性的证明.在MFD 能够被更广泛地应用到网络交通管理和预测等领域之前,建立各因素与MFD曲线关系的定量分析模型,并给出相关参数的确定方法至关重要.这一问题的解决与否,直接影响着MFD 的理论意义与应用价值.
2)面向MFD 的小区最优划分方法 小区是研究MFD 及其应用的基本单元.到目前为止的研究大多集中在静态小区划分上.如何做到小区划分与MFD 的最佳匹配,如何根据实际交通状态进行小区动态划分,都需要进一步研究.
3)网络需求分布特征及其影响的刻画 现有研究对小区内部需求采用固定值或浮动车数据,但只能获取大致的情况.如何更精确的反应出小区内部到达率以及各种不同需求组合对MFD的影响,是另一个值得深入探索的领域.
4)基于MFD 的交通网络管控策略研究 目前的研究大多将小区视为一个单元进行简化的管理控制策略分析.如何针对不同类型的网络及其需求模式,研究具体的基于MFD 的管控策略,是影响MFD 在交通工程领域发挥作用的关键.
6 结束语
MFD 作为小区的特有属性,与外部交通需求无关,少量数据下即可获取MFD.基于以上特点,在已知小区MFD 的前提下,即可依据检测器数据及不同控制方法及措施实现对小区的控制,使得整个小区处于稳定的交通状态.由此可以看出,相较于其他网络分析模型,MFD 理论上应用价值和潜力更大.因而,有关MFD 的研究将进一步走向深入.而随着前述诸多问题的解决,MFD 将在网络交通分析和管控领域发挥更大的作用.
[1]DAGANZO C F.Urban gridlock:Macroscopic modeling and mitigation approaches[J].Transportation Research Part B:Methodological,2007,41(1):49-62.
[2]GEROLIMINIS N,DAGANZO C F.Existence of urban-scale macroscopic fundamental diagrams:Some experimental findings[J].Transportation Research Part B:Methodological,2008,42(9):759-770.
[3]CASSIDY M J,JANG K,DAGANZO C F.Macroscopic fundamental diagrams for freeway networks[J].Transportation Research Record:Journal of the Transportation Research Board,2011(2):8-15.
[4]GONZALES E J,CHAVIS C,LI Y,DAGANZO C F.Multimodal transport modeling for Nairobi,Kenya:Insights and recommendations with an evidencebased model[R].UC Berkeley Center for Future Urban Transport,2009.
[5]姬杨蓓蓓,WINNIE D.阿姆斯特丹城市道路线圈检测器布设方法研究[J].重庆交通大学学报:自然科学版,2010,29(5):754-757.
[6]GAO F.Macroscopic fundamental diagrams for Stockholm using FCD data[D].KTH:School of Architecture and the Built Environment(ABE),2011.
[7]HE Z,HE S,GUAN W.Figure-eight hysteresis pattern in macroscopic fundamental diagrams for urban freeway network in Beijing,China[C]∥Transportation Research Board 92nd Annual Meeting,2013:13-1760.
[8]LECLERCQ L,GEROLIMINIS N.Estimating MFDs in simple networks with route choice[J].Procedia-Social and Behavioral Sciences,2013,80(7):99-118.
[9]GEROLIMINIS N,BOYACI B.The effect of variability of urban systems characteristics in the network capacity[J].Transportation Research Part B:Methodological,2012,46(10):1607-1623.
[10]XIE X,CHIABAUT N,LECLERCQ L.Macroscopic fundamental diagram for urban streets and mixed traffic:cross-comparison of estimation methods[C]∥Transportation Research Board 92nd Annual Meeting,2013:103-105.
[11]DAGANZO C F,GEROLIMINIS N.An analytical approximation for the macroscopic fundamental diagram of urban traffic[J].Transportation Research Part B:Methodological,2008,42(9):771-781.
[12]COURBON T,LECLERCQ L.Cross-comparison of macroscopic fundamental diagram estimation methods[J].Procedia-Social and Behavioral Sciences,2011,20:417-426.
[13]KNOOP V,HOOGENDOORN S.Two-variable macroscopic fundamental diagrams for traffic networks[C]∥Ninth International Conference on Traffic and Granular Flow,2011:1208-1220.
[14]KNOOP V L,HOOGENDOORN S P,LINT J W C V.The impact of traffic dynamics on the macroscopic fundamental diagram[C]∥Transportation Research Board 92nd Annual Meeting,2013:1123-1135.
[15]GEROLIMINIS N,SUN J.Properties of a well-defined macroscopic fundamental diagram for urban traffic[J].Transportation Research Part B:Methodological,2011,45(3):605-617.
[16]GEROLIMINIS N,SUN J.Hysteresis phenomena of a macroscopic fundamental diagram in freeway networks[J].Procedia-Social and Behavioral Sciences,2011,17:213-228.
[17]许菲菲,何兆成,沙志仁.交通管理措施对路网宏观基本图的影响分析[J].交通运输系统工程与信息,2013,13(2):185-190.
[18]朱 琳,于 雷,宋国华.基于MFD 的路网宏观交通状态及影响因素研究[J].华南理工大学学报:自然科学版,2012,40(11):138-146.
[19]MAHMASSANI H S,SABERI M.Urban network gridlock:theory,characteristics,and dynamics[J].Procedia-Social and Behavioral Sciences,2013,80(7):79-98.
[20]BOYACI B,GEROLIMINIS N.Exploring the effect of variability of urban systems characteristics in the network capacity[C]∥Transportation Research Board Annual Meeting,2012:1612-1623.
[21]GEROLIMINIS N,DANÉS J M,ESTRADA A.Multimodal macroscopic fundamental diagram for“car-bus”mixed traffic signalized corridors:application in city of Barcelona,Spain[C]∥Transportation Research Board 92nd Annual Meeting,2013:1013-1089.
[22]ZHENG N,GEROLIMINIS N.On the distribution of urban road space for multimodal congested networks[J].Procedia-Social and Behavioral Sciences,2013,80(7):119-138.
[23]王 玉,段征宇.偶发性交通事件对网络交通状态的影响分析[C]∥第七届中国智能交通年会,2012:22-27.
[24]BUISSON C,LADIER C.Exploring the impact of homogeneity of traffic measurements on the existence of macroscopic fundamental diagrams[J].Transportation Research Record:Journal of the Transportation Research Board,2009(12):127-136.
[25]马莹莹.面向交通小区的交通控制策略研究[D].上海:同济大学,2010.
[26]JIN W L,GAN Q,GAYAH V V.A kinematic wave approach to traffic statics and dynamics in a double-ring network[C]∥Transportation Research Board 92nd Annual Meeting,2013:2813-2870.
[27]Qian X,Baggen I J H,Daamen I W,et al.Application of macroscopic fundamental diagrams to dynamic traffic management[D].ITS Edulab:Rijkswaterstaat &Delft University of Technology,2009.
[28]ZHANG L,GARONI T M,GIER J D.A comparative study of macroscopic fundamental diagrams of arterial road networks governed by adaptive traffic signal systems[J].Transportation Research Part B:Methodological,2013,49:1-23.
[29]ZHAO T T,LI Z H,MU B P,et al.Exploring the influence of real-time traveler information on the macroscopic fundamental diagrams[C].11th International Conference of Chinese Transportation Professionals(ICCTP),2011:155-161.
[30]JI Y,GEROLIMINIS N.On the spatial partitioning of urban transportation networks[J].Transportation Research Part B:Methodological,2012,46(10):1639-1656.
[31]JI Y,GEROLIMINIS N.Spatial and temporal analysis of congestion in urban transportation networks[C]∥Transportation Research Board Annual Meeting,2011:1791-1808.
[32]HADDAD J,GEROLIMINIS N.On the stability of traffic perimeter control in two-region urban cities[J].Transportation Research Part B:Methodological,2012,46(9):1159-1176.
[33]李刚奇,赵娅丽.基于宏观交通理论的交通控制子区划分方法[C]∥第七届中国智能交通年会,2012:31-38.
[34]马莹莹,杨晓光,曾 滢.基于谱方法的城市交通信号控制网络小区划分方法[J].系统工程理论与实践,2010,30(12):2290-2296.
[35]ABOUDOLAS K,GEROLIMINIS N.Perimeter flow control in heterogeneous networks[C]∥13th Swiss Transport Research Conference,2013:1055-1081.
[36]ABOUDOLAS K,GEROLIMINIS N.Perimeter and boundary flow control in multi-reservoir heterogeneous networks[J].Transportation Research Part B:Methodological,2013,55:265-281.
[37]ABOUDOLAS K,GEROLIMINIS N.Feedback perimeter control for multi-region large-scale congested networks[C]∥2013European Control Conference,2013:106-114.
[38]HADDAD J,RAMEZANI M,GEROLIMINIS N.Model predictive perimeter control for urban areas with macroscopic fundamental diagrams[C]∥American Control Conference(ACC),2012:1051-1066.
[39]GEROLIMINIS N,HADDAD J,RAMEZANI M.Optimal perimeter control for two urban regions with macroscopic fundamental diagrams:a model predictive approach[J].Intelligent Transportation Systems,IEEE Transactions 2013,14(1):348-359.
[40]王福建,韦 薇,王殿海,等.基于宏观基本图的城市路网交通状态判别与监控[C]∥第七届中国智能交通年会,2012:72-79.
[41]EKBATANI M K,KOUVELAS A,PAPAMICHAIL I,et al.Exploiting the fundamental diagram of urban networks for feedback-based gating[J].Transportation Research Part B:Methodological,2012,46(10):1393-1403.
[42]EKBATANI M K,PAPAGEORGIOU M,PAPAMICHAIL I.Urban congestion gating control based on reduced operational network fundamental diagrams[J].Transportation Research Part C:Emerging Technologies,2013,33:74-87.
[43]TOSHIO Y S,YU J,YONE Z W,et al.Evaluation of an area metering control method using the macroscopic fundamental diagram[C]∥Transportation Research Part B Annual Meeting 2010:1110-1141.
[44]RAMEZANI M,HADDAD J,GEROLIMINIS N.Cooperative traffic management of mixed freeway and urban networks[C]∥Transportation Research Board 92nd Annual Meeting,2013:1813-1825.
[45]DAGANZO C F,GONZALES E J,GAYAH V.Traffic congestion in networks,and alleviating it with public transportation and pricing[R].Institute of Transportation Studies,University of California,Berkeley,2011.
[46]KNOOP V,LINT J V,HOOGENDOORN S.Routing strategies based on the macroscopic fundamental diagram[J].Transportation Research Record:Journal of the Transportation Research Board,2012,2315(1):1-10.
[47]LIN S,ZHOU Z,XI Y.Analysis of performance criteria for model-based traffic congestion control in urban road networks[C]∥Transportation Research Board 92nd Annual Meeting,2013:1713-1775.
[48]ZHENG N,WARAICH R A,AXHAUSEN K W,et al.A dynamic cordon pricing scheme combining the macroscopic fundamental diagram and an agentbased traffic model[J].Transportation Research Part A:Policy and Practice,2012,46(8):1291-1303.
[49]HORIGUCHI R,IIJIMA M,HANABUSA H.Traffic information provision suitable for TV broadcasting based on macroscopic fundamental diagram from floating car data[C]∥Intelligent Transportation Systems(ITSC),2010:1051-1071.
[50]GAYAH V V,DIXIT V V.Using mobile probe data and the macroscopic fundamental diagram to estimate network densities:tests using micro-simulation[C]∥Transportation Research Board 92nd Annual Meeting,2013:1413-1493.
