基于HyperMesh的运输车车架有限元分析

廖世业，夏绪辉，冯 勋

LIAO Shi-ye, XIA Xu-hui, FEN Xun

(武汉科技大学 机械自动化学院，武汉 430081)

0 引言

车架作为车辆重要的承载部分，运输车中多数零部件如：驾驶室，发动机，变速箱，车桥等通常都直接与车架相连接。在运动过程中，车架还承受各零部件产生的各种力与力矩的影响，承载情况的复杂性要求车架必须有足够的刚度和强度来避免其主体发生变形或者断裂的现象，以保证其安全可靠性及使用寿命[1,2]。但是，在以往的设计过程中，设计人员大多采用经验公式进行计算，这种方法并不能精准的计算出车架各部件应力和形变[3]。本文采用HyperWorks软件对车架结构进行有限元分析，运用Radioss及OptiStuct求解器分析了车架的应力和位移形变分布状态及自由模态分析，利用分析结果验证该车架设计的合理性，对后续的结构优化提供理论依据。

1 车架的几何模型及有限元模型

本文以某造船厂运输车车架为研究对象，该车架由型钢焊接而成，两根纵梁为矩形截面型钢，总长9440mm，大梁式，前后等宽，纵梁最大断面尺寸为360mm×140mm×20mm，横梁最大断面尺寸为300mm×140mm×20mm，前后端横梁为Π型槽钢，中间横梁为矩形截面型钢，横梁的长度为920mm。

实际中，车架的形状结构复杂，支撑装置和固定装置多种多样，除几何形体不规则外还存在许多倒圆角和圆孔，如果在建模的过程中将这些细微之处全部考虑在内，就会导致网格的密度很大，单元尺寸极小，节点方程的数量庞大，因而增加求解时间，同时局部的网格质量无法保证，容易导致求解失真。因此，有必要对车架的结构进行合理的简化，建立合理有效的模型，从而减少分析过程中的计算量，提高计算效率。

运用Pro/E三维建模软件对简化处理后的车架结构进行实体建模，为了避免部分零件出现几何缺陷或数据丢失的情况，我们通常将Pro/E中建立的模型保存为.iges格式文件，把该格式文件直接导入HyperMesh中进行后续的网格划分。

对实体模型进行网格划分首先需要对网格单元定义属性，其次定义网格的生成控制，最后划分网格。其中网格的单元属性包括网格单元类型，实常数以及材料特性。本文车架的材质选用16Mn，其杨氏模量为2.06×1011Pa，泊松比为0.28，材料密度为7800kg/m3，屈服应力为345MPa。本文采用HyperMesh中的自动网格划分功能对已建好的实体模型进行单元网格划分，最后得到了车架有限元模型（如图1所示）。使用HyperMesh中的count功能，可以得出其单元网格个数106472，节点个数53268。

图1 车架有限元模型

2 车架静态工况分析

车架作为重要的承载部分，这就要求其既要有足够的强度，也要有足够的刚度。足够的弯曲刚度，可使车架上的部件在行驶过程中相对位置不发生改变。车架刚度不足，会引起振动和噪声，也会使汽车的乘坐舒适性、操纵稳定性及某些基件的可靠性下降，然而其扭转刚度不易过大，否则汽车的通过性变差[4]。

运输车在行驶过程中，在所有轮胎都着地情况下，地面对整车的作用力依次通过轮胎、车桥、板簧、吊耳销最终传至车架上，因此，我们可以在吊耳销处创建约束点。对于本文中的车型，动力总成及满载时的总质量为16t，将这部分总质量的以均匀分布的方式加载到0～7000mm范围内；驾驶室及乘员的总质量为1.3 t，同样以均匀分布的方式将该部分总质量加载到7560mm～9440mm范围内，这样就对整个车架进行了全部加载，如图2所示。

图2 车架加载与约束

2.1 车架弯曲工况分析

运输车车架纵梁断面的最大弯曲应力σ为：

W为纵梁在断面处的弯曲截面系数。

式中：h为槽形断面的腹板高；

b为翼缘宽；

t为断面厚度。

但是运输车车架纵梁的弯曲应力不应大于其材料的许用应力。

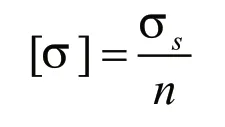
式中：σs为材料屈服极限，车架的材料为16Mn，σs取值为340MPa～360MPa；

n为安全系数，一般取值为1.4。

因此车架纵梁断面的最大弯曲应力σ 在242.9MPa～257.14MPa之间。

将吊耳销处进行全约束（图2），使用HyperWorks自带的Radioss求解器进行求解计算后，我们可以在Post后处理工具中使用Contour功能查看车架弯曲工况下的位移（图3）和应力（图4）云图。

图3 车架弯曲位移图

图4 车架弯曲等效应力图

从位移和应力云图可以看出，当车架发生纯弯曲时，纵梁是应力与位移的主要承受体，而横梁几乎没有承受应力，可以忽略。由于车架后部承受的载荷较前部大很多，位移变化主要出现在车架尾部和车架中部的悬空承处，车架前部基本没有发生位移变化，最大位移出现在车架中部悬空处，最大位移值为3.83mm。应力主要出现在施加约束的吊耳销处，最大应力的位置为靠近车架尾部的吊耳处，最大应力值为76.4MPa。

2.2 车架扭转工况分析

当运输车行驶在路面上时，由于路面会出现凹凸不平的情况，这样运输车就会受到扭转载荷的作用，其极限扭转载荷为运输车在非对称支撑下产生的静态扭转状态。本文模拟车轮过障碍物的情况，即假定左前轮被抬升，右前轮被拉低。如图5、图6所示。

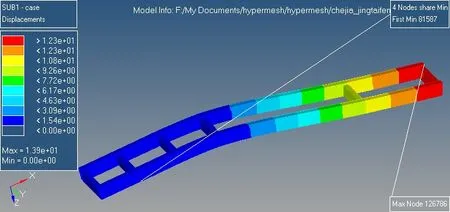
图5 车架扭转位移图

图6 车架扭转等效应力图

从图5和图6可以看出，由于对前轮的约束发生改变，位移在车架前端的变化十分明显，运输车左轮被抬升，导致其最大位移出现在左纵梁的前端，其最大位移值为13.9mm，位移变化由纵梁前端向后端逐渐变小，而车架后端由于对吊耳销的约束并未发生改变，因而车架后端基本上没有发生位移变化。车架的应力依然出现在施加约束的吊耳销处，但较弯曲工况而言，扭转工况下的应力在第三根横梁与纵梁连接处出现的区域要大很多，说明该区域有应力集中现象，最大应力出现在靠近车架尾端的吊耳销处，其最大应力值为215MPa。

取车架的安全系数为1.5。材料的屈服极限[σ ]为280MPa～350MPa。

虽然没有超过材料的最大屈服极限，但是与其他部位相比其属于高应力区，说明该工况下车架还是比较危险的。

3 车架模态分析

所谓模态分析，就是确定设计结构或机械零部件的振动特性，得到结构固有频率和振型的过程，它是动态设计的核心。研究的是结构模态即自由模态，是结构本身的特性与材料特性所决定的，与外载条件等无关（即无需加任何载荷和约束），而结构在任意初始条件及外载作用下的强迫振动都可以由结构按这些基本特性的强迫振动的线性组合构成[5]。本文通过不施加载荷与约束，对车架的有限元模型进行自由模态分析，得到的车架前6阶固有频率与振型描述如表1所示。

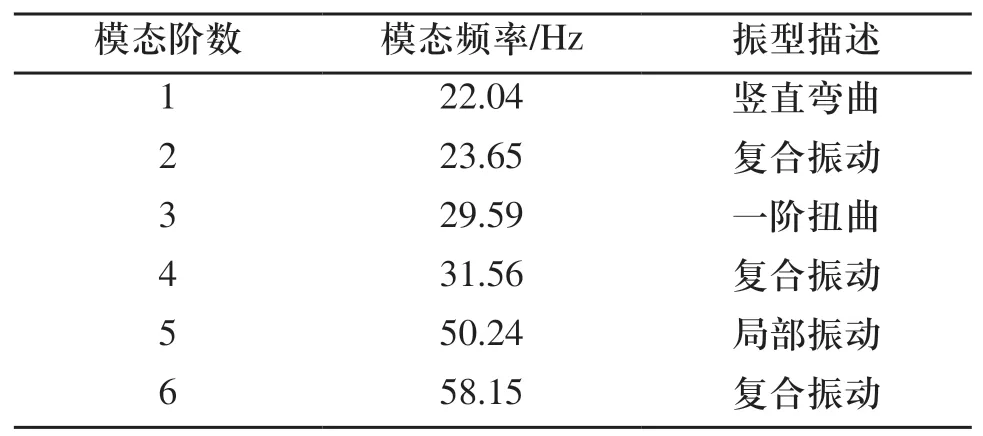
表1 车架固有频率与振型描述

图7和图8分别给出了相应的第1阶和第2阶振型图。

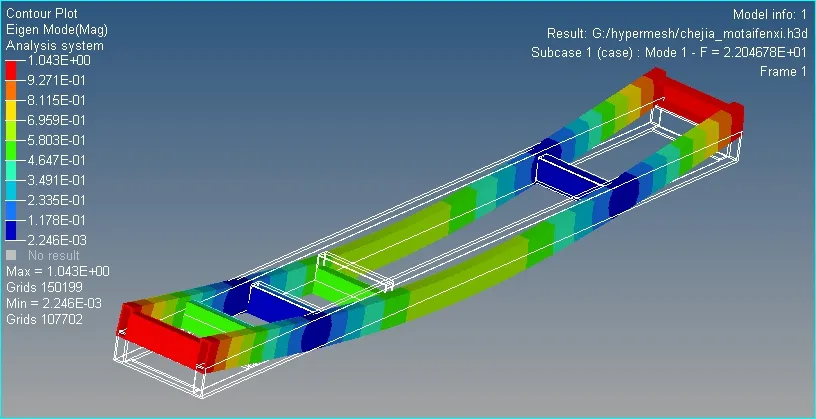
图7 车架第1阶振型

由振型图我们可以得出，第1阶是车架沿竖直方向的弯曲振型，当以该阶模态振动时，整个车架产生了弯曲振动，车架前后端横梁处振幅较大；第2阶是车架的复合振动振型，当以该阶模态振动时，整个车架产生了扭转弯曲的复合振动，车架尾端横梁处振幅较大。

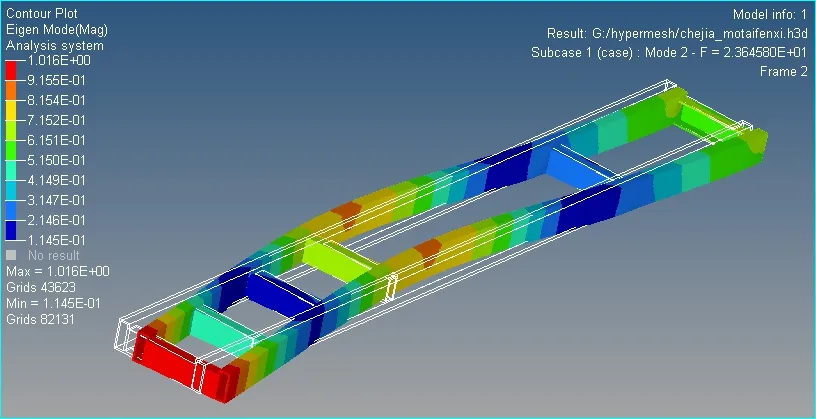
图8 车架第2阶振型

由图9的模态变化曲线图可以得知，车架模态较为分散，在模态频率与模态阶次的递增关系中，车架的模态频率变化平缓，没有出现突变的现象。

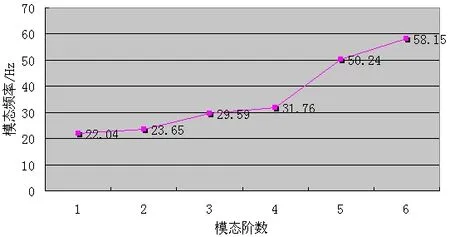
图9 模态变化曲线图

4 结论

本文应用有限元分析法对运输车车架进行了静态应力和模态分析，通过静态应力分析可知，在给予车架弯曲工况与扭转工况的情况下，车架的最大应力值始终都小于车架的屈服应力值，说明该车架是符合设计要求的。但是由于扭转工况下的最大应力值较弯曲工况下的最大应力值大很多，这一点还有待我们进一步优化解决。车架的固有频率一般为10Hz～15Hz，目前在高速公路和较好城市路面不平引起的激励频率一般为1Hz～20Hz的垂直振动。由模态分析可知，车架的各低阶模态的频率值在22.04Hz左右，避免了各种激励频率与车架形成共振的影响，保证了运输车行驶的稳定性与安全性。

综合而言，通过对车架进行有限元分析，为我们在对该类车架设计提供重要的参数，为改进结构设计提供了理论依据，同时也为深入研究相关问题奠定基础。

[1]张润生,侯炜.车架刚度及强度的有限元分析[J].拖拉机与农用运输车,2007(8):29-31.

[2]吕东升,王东方,苏小平.基于的HYPERWORKS某客车车架有限元分析[J].机械设计与制造,2011(3):11-12.

[3]高卫民,王宏雁.汽车结构分析有限元法[J].汽车研究与开发,2000(6):30-32.

[4]黄华,茹丽妙.重型运输车车架动力学分析[J].车辆与动力技术,2001(2):40-44.

[5]汪伟,辛勇.车架有限元建模及模态分析[J].机械设计与制造,2009(11):53-54.