具有跳跃和时间周期势的Duffing方程的Lagrange稳定性*

李红霞

（中国海洋大学数学科学学院，山东 青岛 266100）

0 引言

1960年代Littlewood［1］研究了Duffing方程

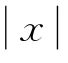
在半线性方程中，具有跳跃项的Duffing方程是一个非常重要的形式：

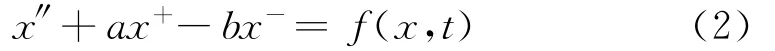
其中：a和b是正常数，a≠b，x＋＝max｛x，0｝，x－＝max｛－x，0｝，f（x，t＋2π）＝f（x，t）。当f只与t有关时，Ortega［6］研究了 Duffing型方程

去掉了ε任意小的假设后，仍可利用扭转定理得到方程的Lagrange稳定性。

最近，Wang［9］研究了 Duffing型方程

其中p（t）∈C6（S1），S1＝R/2πZ，扰动项φ（x）为有界函数，利用Ortega给出的扭转定理证明了方程的Lagrange稳定性；当扰动项φ（x）为无界函数时有相同结论［10］。注意到都没有考虑扰动项带有时间周期势的情况。

2012 年，Jiao、Piao和 Wang［11］研究了较为一般的Duffing方程

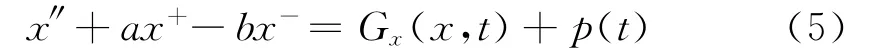
利用Moser小扭转定理证明了方程的Lagrange稳定性，但文中对G（x，t），p（t）的光滑性要求较高。另外，文献［12-14］等研究了扰动项满足其它条件的Duffing方程的Lagrange稳定性。

受上述文献启发，本文考虑扰动项依赖于时间变量t的Duffing型方程

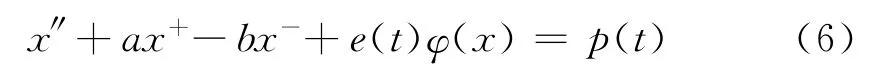
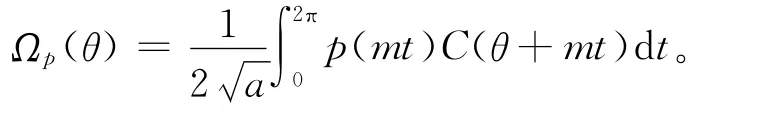
对变量θ求偏导，得

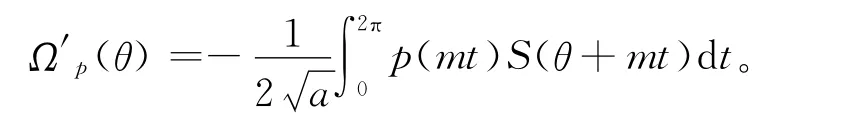
这里函数C（t）、S（t）的性质详见文献［9，17］。记＝，则Ψ（0）＝0。

规定c＜1和C＞1是2个通用的正常数。本文的结论是2个定理，如下：

则方程（6）具有Lagrange稳定性。

注1 由（7）（8）及L’Hospital法则易知，

（H4）e（t），p（t）∈C7（S1）；

则（6）具有Lagrange稳定性。

注2（定理的证明思路） 先利用典则变换，将（6）变换为一个可积的 Hamilton系统，其次根据Ortega［15－16］给出的扭转定理，得到任意大的不变曲线存在，不变曲线微分同胚于（x，x′）平面上围绕原点的圆环，并将（6）的解曲线限制在它的内部，从而保证了（6）的所有解是有界的，即（6）具有Lagrange稳定性。

1 预备知识

对于本节中所有引理，均假设条件（H1），（H2）成立。显然，当（H1），（H2）成立时，（H4），（H5）一定成立。

方程（6）等价于下面的非自治Hamilton系统：

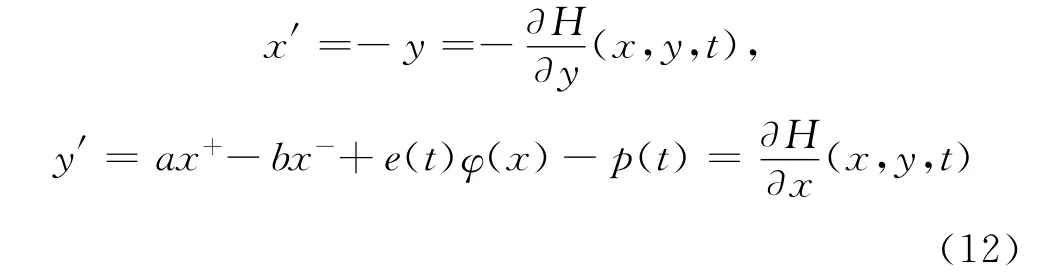
其中

引理1 对 任 意 的 （x0，y0）∈ R2，t0∈ R，非 自 治Hamilton系统（12）在整个t-轴上存在满足z（t0）＝（x0，y0）的解z（t）＝（x（t；t0，x0，y0），y（t；t0，x0，y0））。证明 由于φ（x）是有界的，e（t），p（t）是2π周期的光滑函数，所以存在常数M＞0，使得

利用微分基本不等式，得

根据不等式及F（t）的定义知，

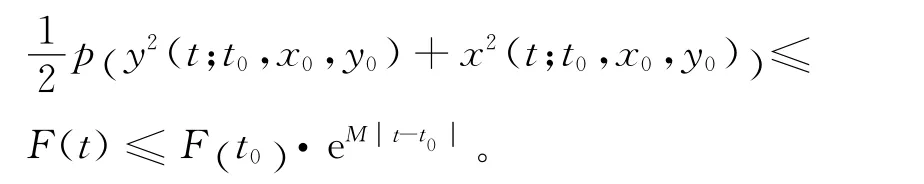
所以，系 统 （12）的解z（t）＝（x（t；t0，x0，y0），y（t；t0，x0，y0））在整个t-轴上存在。

利用变换（r，θ） （x，y）：

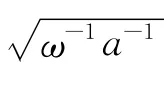
注3 类似于文献［5］中的结论，有

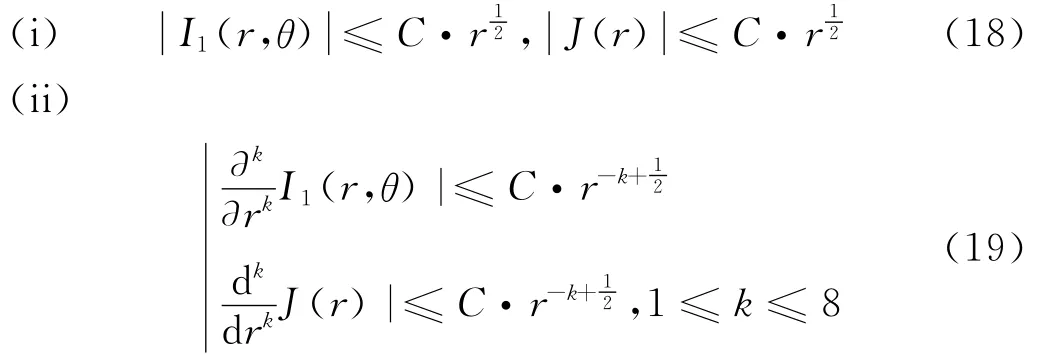
注4 （i）容易验证

（ii）假设

则函数φ（r）是有界的，并且

2 典则变换

本节给出Hamilton系统（14）的典则变换。根据隐函数定理，存在函数R＝R（h，t，θ），使得

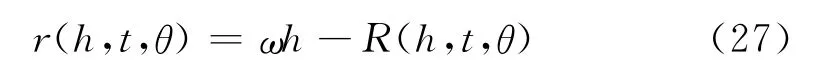
因此，（14）可以转化为：

再由（15）和（24）得，R满足（20）。根据注3（ⅳ）得，Hamilton函数为：

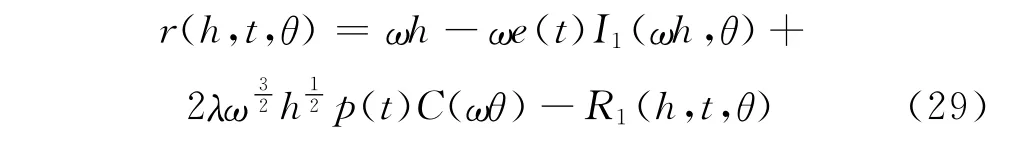
令e1（t）＝e（t）－，则，从 而Hamilton函数为：

引理2 存在典则变换Φ1：

其中U、V关于θ是2π周期函数。在此变换下，r（h，t，θ）变换为：

新的扰动项满足：

证明 假设变换Φ1为：

其中生成函数S1＝S1（μ，t，θ）待定。通过变换Φ1，相应的Hamilton函数为：

令ωtS1－ωe1（t）I1（ωμ，θ）＝0，则存在生成函数

且V（μ，ν，θ）＝μS1（μ，t，θ），U（μ，ν，θ）＝tS1（μ，t，θ），继而得到新的Hamilton函数

根据注3及S1（μ，t，θ）的表达式可知，（32）成立。引理3 存在典则变换Φ2：

其中T（ρ，θ）关于θ是2π周期函数。在此变换下，Hamilton函数（31）变换为：

新的扰动项满足：

证明 假设变换Φ2为：

生成函数S2＝S2（μ，τ，θ）在下面的证明中得到。通过变换Φ2，Hamilton函数（μ，ν，θ）变换为：

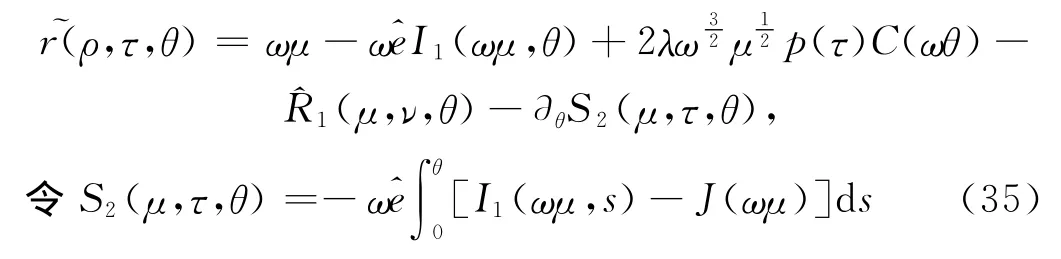
显然生成函数S2存在，与τ无关，并且关于θ是2π周期函数。故存在ρ＝μ，T＝μS2，且

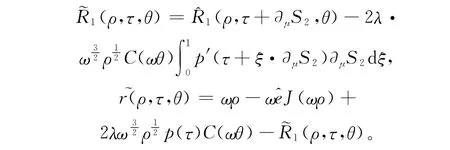
易知，

由的估计及（36），可得（34）成立，详见文献［9］。

3 定理的证明

本节利用Ortega给出的扭转定理的变形证明2个定理。考虑典则变换后的Hamilton系统

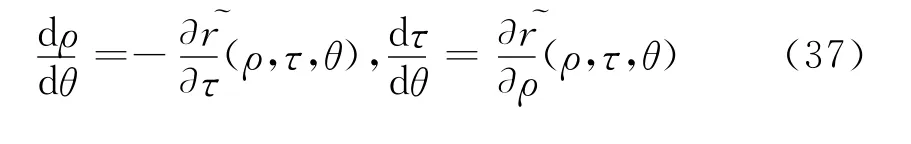
3.1 定理1的证明

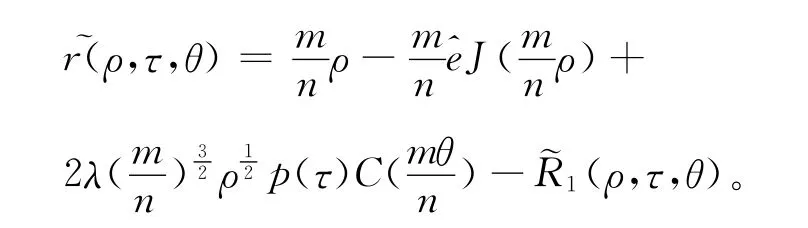
引入新变量（υ，）满足，其中υ∈。显然，系统（37）变换为：

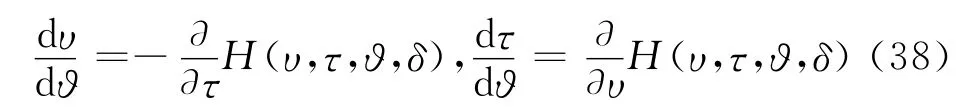
相应的Hamilton函数为：

由（25）知，

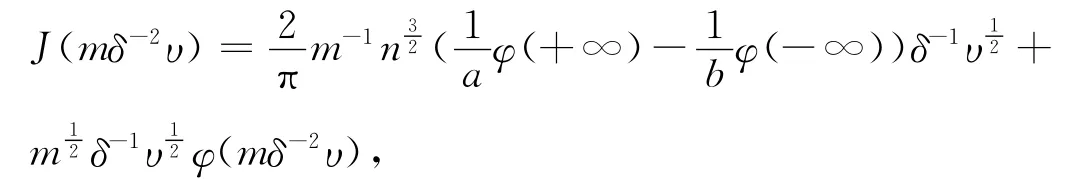
将J（mδ－2υ）代入 Hamilton函数H（υ，τ，，δ），得

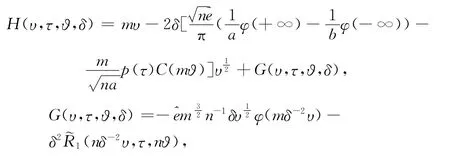
根据注4和引理3，当δ→0＋时，得

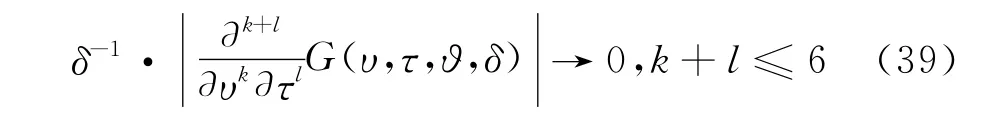
新的Hamilton函数H（υ，τ，，δ）代入系统（38），得

在初始条件（υ（0，υ0，τ0），τ（0，υ0，τ0））＝（υ0，τ0）下，系统（40）存在解（υ（，υ0，τ0），τ（，υ0，τ0）），可假设为：

因此，系统（40）的Poincare映射P1为：

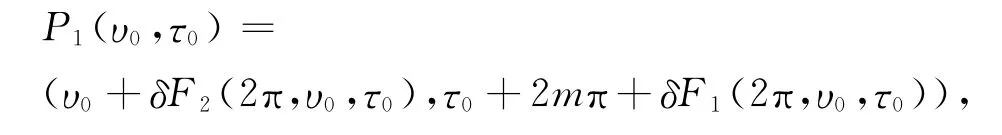
对（41）式两端求导得，

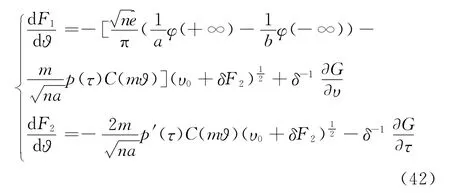
其中：F1（，υ0，τ0），F2（，υ0，τ0）＝O5（1）［17］，且满足

由（42）直接计算知，

故Poincare映射P1的表达式为：

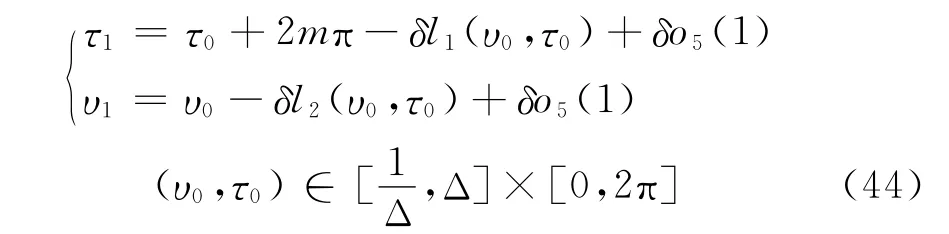
其中

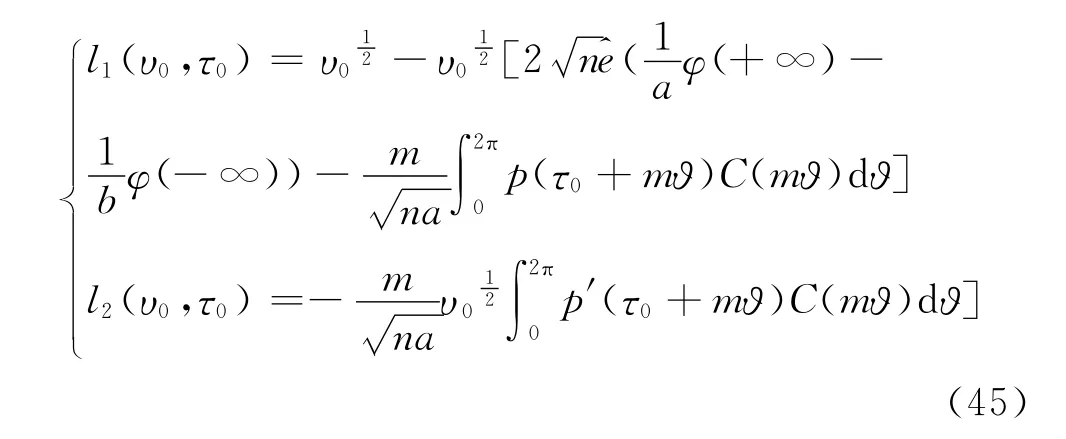
但标准Moser扭转定理不适用于此种Poincare映射。对于此难点参考Ortega［15］给出的Moser小扭转定理的推广，运用它证明Poincare映射P存在不变曲线，这就保证了系统具有Lagrange稳定性。下面证明P1满足文献［15］扭转定理的条件。

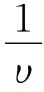
其中

3.2 定理2的证明

在新的作用和角变量（γ，τ）下，系统（37）变换为：

相应的Hamilton函数为：

由（26）知，

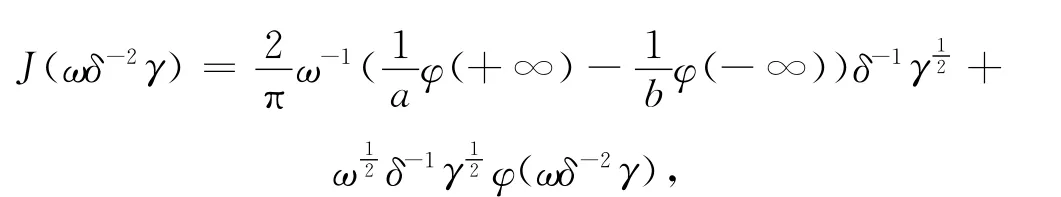
将J（ωδ－2γ）代入 Hamilton函数H（γ，τ，θ，δ），得

易证当δ→0＋时，

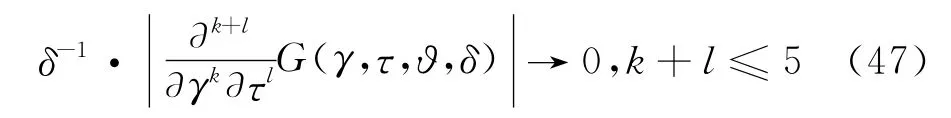
假设（46）的解（γ（θ，γ0，τ0），τ（θ，γ0，τ0））为：

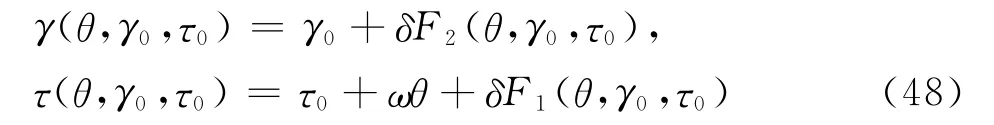
记（4.11）的Poincare映射P2为：

类似与3.1节内容，Poincare映射P2为：

其中

容易验证Poincare映射P2满足文献［16］中Ortega给出的扭转定理的条件，所以Poincare映射存在不变曲线，这保证了系统具有Lagrange稳定性。

［1］Littlewood J.Unbounded solutions of an equation of¨y＋g（y）＝p（t）withp（t）periodic and bounded andg（y）/y→∞asy→±∞［J］.Journal of London Mathematical Society Lond Math Soc，1966，41：497-507.

［2］You J.Boundedness for solutions of superlinear Duffing’s equations via twist curves theorems［J］.Science in China A，1992，35：399-412.

［3］Levi M.Quasiperiodic motions in superquadratic time-periodic potentials［J］.Commhnication in Mathematical Physics，1991，143（1）：43-83.

［4］Kupper T，You J.Existence of quasiperiodic solutions and Littlewood’s boundedness problem of Duffing equations with subquadratic potentials［J］.Nonlinear Analysis，TAM，1999，35：549-559.

［5］Liu B.Boundedness in nonlinear oscillations at resonance ［J］.Journal of London Mathematical Society，Differential Equations，1999，153：142-174.

［6］Ortega R.Asymmetric oscillators and twist mappings［J］.J London Math Soc，1996，53：325-342.

［7］Liu B.Boundedness in asymmetric oscillations ［J］.Journal of Mathematical Analysis and Applications，1999，231：355-373.

［8］Fabry C.Behavior of forced asymmetric oscillators at Resonance［J］.Electronic Journal of Differential Equations，2000，74：1-15.

［9］Wang X.Invariant Tori and Boundedness in Asymmetric Oscillations［J］.Acta Mathematica Sinica，English Series，2003，19：765-782.

［10］Yuan X.Quasiperiodic motions for asymmetric oscillators［J］.Acta Mathematica Sinica，English Series，2001，17：253-262.

［11］Jiao L，Piao D，Wang Y.Boundedness for the general semilinear Duffing equations via the twist theorem ［J］.Journal of Differential Equations，2012，252：91-113.

［12］Capietto A，Liu B.Quasiperiodic solutions of a forced asymmetric oscillator at resonance［J］.Nonlinear Analysis，TAM，2004，56：105-117.

［13］Fabry C，Mawhin J.Oscillations of a forced asymmetric oscillator at resonance［J］.Nonlinearity，2000，13：1-13.

［14］Fabry C，Mawhin J.Properities of solutions of some forced nonlinear oscillators at resonance［C］.Proceedings of International Conference of Nonlinear Analysis，Tianjin：Nankai University，2000.

［15］Ortega R.Boundedness in a piecewise linear oscillator and a variant of the small twist theorem［J］.Proceedings of London Mathematical Society，1999，79：381-413.

［16］Ortega R.Invariant curves of mappings with averaged small twist［J］.Advanced Nonlinear Studies，2001，1：14-39.

［17］Alons J M，Ortega R.Roots of unity and unbounded motions of an asymmetric oscillator［J］.Journal of Differential Equations，1998，143：201-220.