基于时延差的声纳浮标阵定位仿真＊

（海军潜艇学院 青岛 266071）

1 引言

航空反潜凭借其机动快速、安全性高等特点在反潜作战中发挥着重要作用。在搜索潜艇过程中，反潜机可以使用声纳浮标、吊放声纳等设备。主动声纳浮标虽具有探测精度高的特点，但是容易被敌潜艇侦察到进而进行规避，对抗反潜机侦测。被动声纳浮标通常只能进行定向，无法定位，但是凭借其隐蔽性高效性的特点在反潜对抗中发挥重要作用。在我国海军奔向深蓝的征途中，执行远海反潜任务时，反潜机携带声纳浮标能迅速到达指定海区完成任务，可将机动性的优势转化为战场优势。

2 被动声纳浮标时延差法对目标定位分析

假设目标位置与声纳浮标位置关系如图1所示。

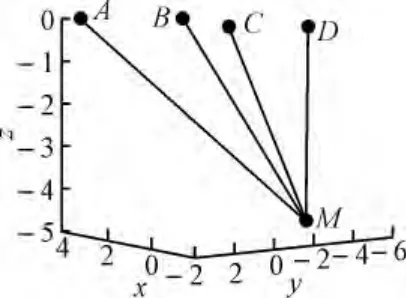
图1 阵元空间关系示意图

M点为敌潜艇位置，其坐标为M（x，y，z），反潜机投放的被动声纳浮标坐标分别为A（x0，y0，z0），B（x1，y1，z1），C（x2，y2，z2），D（x3，y3，z3），在陆地上调节水听器没入海面深度，使四个水听器具有相同的纵坐标，则声纳浮标在一定空间位置内可认为四个声纳浮标纵坐标均为0。目标到达水听器距离为s0，s1，s2，s3，发出噪声信号到达水听器时间分别为t0，t1，t2，t3，则可近似可得［1～3］：

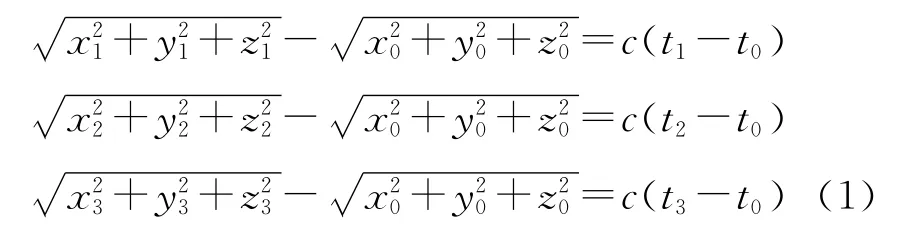
令τ10＝t1-t0，τ20＝t2-t0，τ30＝t3-t0，则有：

已知时延差，取一点为坐标原点，其他三个传感器空间坐标为

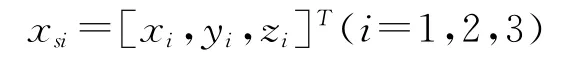
第i个传感器到参考传感器的时延差为τi，τ0为目标到参考传感器的时间，目标坐标为xT＝［xT，yT，zT］T，则有：

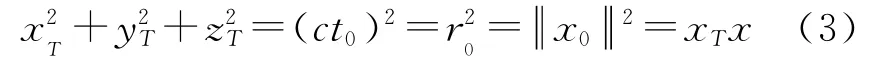
其中‖x0‖2表示x的L2范数。

由空间几何关系知：

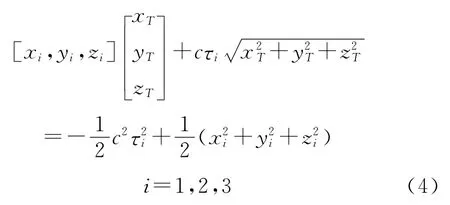
写成矩阵形式则有：

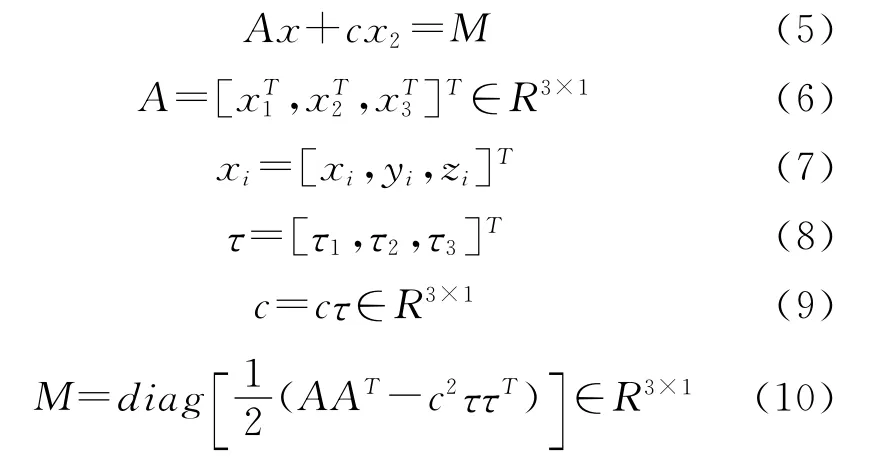
RM×N表示M个元组的集合，每个元组有N个元素。对于M＝3的情况，A是满秩的，因此可以利用式（5）得：

代入式（3）得

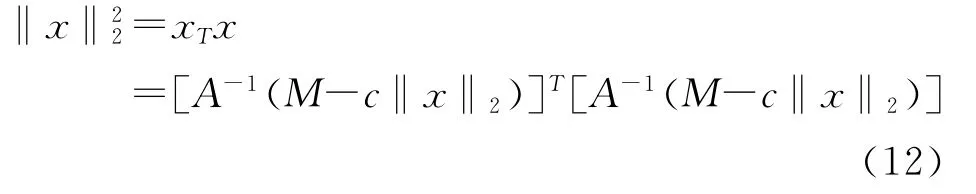
令

则式（12）变为

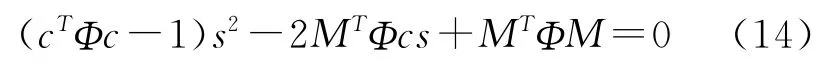
上式为变量s的一个标量二次方程。此处的s为目标到参照传感器之间的距离，且为正数。则由此可以得出目标的距离，将其代入式（11）中可以得到目标方位坐标［4～5］。

3 插值法提高时延估计精度

以三元直线阵为例，设目标距离参考阵元为r，阵元间距为d，目标与阵元直线夹角为θ，则远场下，距离r为

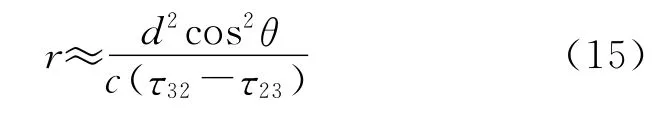
估计量的方差：

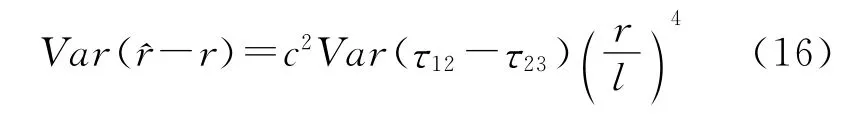
其中l＝dcosθ称为等效基阵的半长，Carter曾证明过其接近克拉美罗下界［6～7］，式（16）开方可以写成：

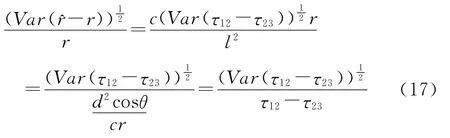
该式等价于：

由误差分析知，时延估计精度对目标定位精度影响较大。原始信号经滤波后进行数据采集，采用互相关法估计时延差。数据采集速度受硬件条件制约，因此可以采用插值法增加数据点数，提高时延估计精度。也可以通过提高阵元间距来提高时延估计精度［8～9］。

对时延估计的仿真如下：

截取频率为8000Hz的wav音频信号作为目标噪音信号，并由Matlab采集。构造0．6506s延迟信号，对两路信号做互相关分析，并对两路信号进行Lagrange差值处理后进行互相关时延估计，分析两次时延估计值。仿真结果如下：

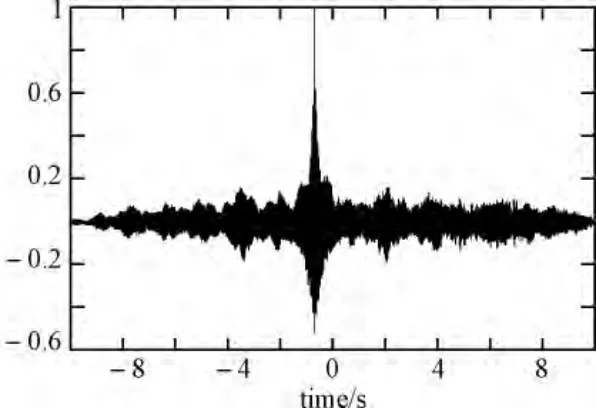
图2 无插值下互相关时延估计

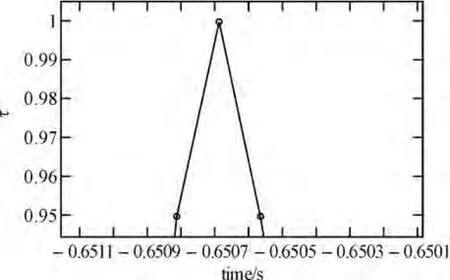
图3 无插值下相关峰示意图

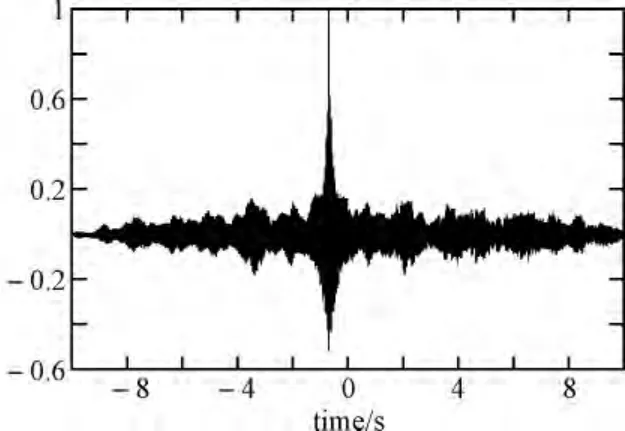
图4 Lagrange插值后互相关时延估计

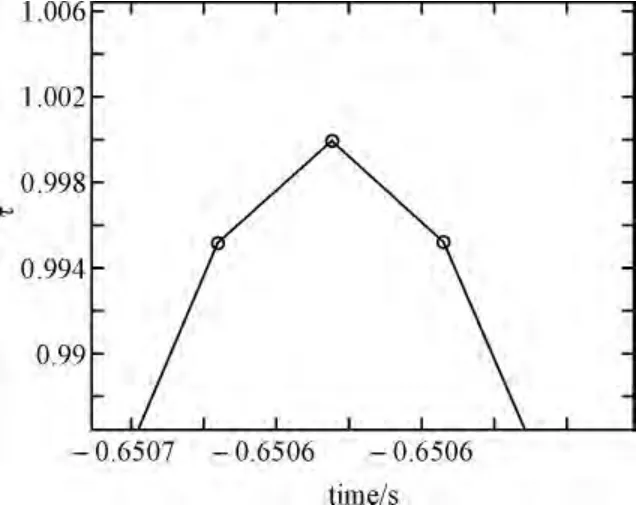
图5 Lagrange插值后相关峰示意图

在数据采集过程中，设采样频率为Fs，则相邻点的时间间隔为1／Fs，时延估计间隔最大误差为1／2Fs。由Runge定理知，当插值点过多时误差增大，因此取四点内插较为理想。由仿真结果可知，在无内插情况下，相关峰峰值位于0．6507s处，采用内插后，相关峰回归到0．6506s位置，时延估计精度提高。

4 结语

本文对四元被动声纳浮标阵的定位原理进行了阐述，分析了影响该方法的主要误差因素，得出通过插值法可以提高时延估计精度进而提高定位精度的结论，并对插值法进行了仿真。本文所采用的仿真数据都是在理想条件下进行的仿真。在未来反潜作战中，基于隐蔽性的反潜搜索将发挥越来越重要的作用。声纳浮标被动工作可以达到隐蔽性要求，但是由于其位于海表，受海表各种反射信号干扰较大，定位精度不高［10］。通过被动定位阵能够抑制部分反射信号，减少干扰，提高定位精度，对反潜搜索过程有一定的帮助［11］。

［1］王新勇．互谱法被动测距改进研究［D］．哈尔滨：哈尔滨工程大学，2004．

［2］刘聪锋．无源定位与跟踪［M］．西安：西安电子科技大学出版社，2011：27-32．

［3］熊辉，雷斌．被动定位系统中时延估计算法的仿真分析［J］．技术平台，2011（3）：47-49．

［4］王昭，李宏，赵俊渭，等．空气声被动定位的误差分析［J］．应用声学，2000，19（2）：39-43．

［5］毛卫宁．水下被动定位方法回顾与展望［J］．东南大学学报（自然科学版），2001，31（6）：129-132．

［6］王成，李少洪，王鑫全，等．测时差被动定位算法的研究［J］．系统工程与电子技术，2001，23（11）：9-12．

［7］马雯，黄建国．广义相关时延估计在被动定位系统中的应用研究［J］．探测与控制学报，2000，22（3）：51-54．

［8］殷世民，付小宁，刘上乾，等．对固定平台红外单站被动定位技术研究［J］．光子学报，2004，33（2）：237-239．

［9］崔玮玮，曹志刚，魏建强，等．声源定位中的时延估计技术［J］．数据采集与处理，2007，22（1）：90-99．

［10］童峰，许肖梅，方世良，等．一种单频水声信号多径时延估计算法［J］．声学学报，2008，33（1）：62-68．

［11］行鸿彦，唐娟．时延估计方法的分析［J］．声学技术，2008，27（1）：110-114．