一种新的雷达间隙辅助红外的机动目标跟踪算法＊

（海军驻南京地区航天机电系统军事代表室 南京 210006）

1 引言

红外传感器不发射电磁波，通过接受目标产生或反射其它能源的辐射，得到量测信号。因此，具有较强的抗电磁干扰能力和隐蔽性；能够有效地躲避反辐射导弹的追踪与打击。但是，红外传感器不能提供目标的距离信息，在跟踪过程中存在强非线性、弱可观测性等问题，致使滤波稳定性较差，且容易发生数值奇异现象。而雷达测距精度高，跟踪性能好，跟踪算法成熟。但是雷达由于其自身的辐射，很容易受到反辐射导弹的攻击，因此在作战时，若能利用雷达短时开机获得的距离信息，辅助红外的俯仰和方位角信息，可实现对目标较好的隐蔽跟踪。所以，雷达间隙辅助红外跟踪，已成为国内外跟踪界研究的热点［1～7］。

针对无源跟踪系统，国内外学者作了大量的工作，文献［8～10］提出了一些用于无源跟踪的滤波算法。本文在雷达间隙辅助红外的跟踪系统中，提出了两层交互式自适应滤波算法，极大地提高了跟踪精度和减小了雷达的开机时间。

2 目标运动模型

目标的离散状态方程为［11］

其中：X（k）为状态向量；F（k）为状态转移矩阵；G（k）为输入控制项矩阵；u（k）为已知输入或控制信号；V（k）是均值为零、方差为Q（k）的高斯白噪声。

雷达的量测方程为

其中：vrR（k）～N（0，），vθR（k）～N（0，），vφR（k）～N（0，），为量测噪声。

红外传感器只能测量目标的方位角θⅠ（k）及俯仰角φⅠ（k），其量测方程为：

其中：vθⅠ（k）～N（0，），vφⅠ（k）～N（0，）为量测噪声。

3 两层交互式自适应滤波算法

3．1 滤波算法结构

雷达间隙辅助红外的结构图如图1，其思想是：在航迹起始阶段，控制雷达开机，当航迹起始质量达到要求后，根据跟踪精度判断雷达是否可以关机；若雷达关机，采用红外单独进行后续跟踪，此时根据双门限与跟踪误差的大小来自适应的选择IMM—EKF或IMM—PF；若雷达开机，采用雷达、红外联合进行后续跟踪，此时采用两层交互式滤波算法，定义联合量测，然后将基于雷达量测的滤波结果和红外量测的滤波结果在外层进行交互，每个模型的滤波结果在内层进行交互，从而充分利用雷达和红外的量测信息，达到对机动目标较好的跟踪。

3．2 滤波算法实现

1）模型集选择［11］

对基于雷达量测的滤波，模型集为：匀速运动，匀加速运动，水平转弯模型。

对基于红外量测的滤波，模型集为：匀速运动，匀加速运动，水平转弯模型，singer模型。

匀速运动的状态方程为

匀加速运动的状态方程为

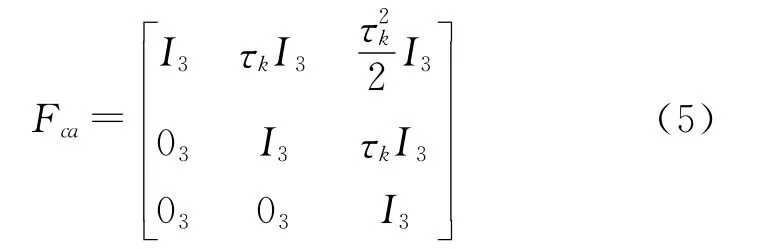
水平转弯模型的状态方程为

Singer模型的状态方程为

其中：Ⅰ3为3×3的单位矩阵，03为3×3的全零矩阵，τk＝tk-tk-1为采样间隔，ω为转弯角速度，α为机动常数的倒数。

图1 雷达间隙辅助红外跟踪的结构图

2）两层交互式滤波算法

内层交互式滤波算法：

（2）计算各模型概率更新值。若模型i的预测残差为，协方差为，那么模型i的似然函数为

模型i的概率更新如下：

（3）计算各模型交互后的滤波结果：

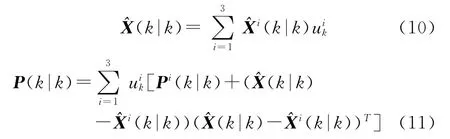
外层交互式滤波算法：

（1）定义雷达与红外在k时刻的联合量测信息z（k）：

（2）计算滤波残差和协方差：

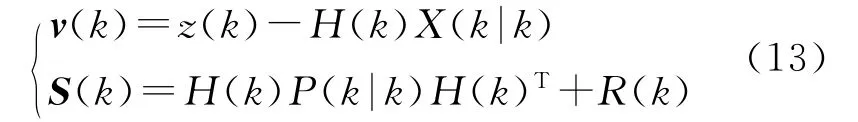
（3）计算k时刻雷达或红外的后验概率：

其中λ（k）为k时刻的似然函数。在高斯假定下

（4）计算雷达和红外交互后的滤波结果：

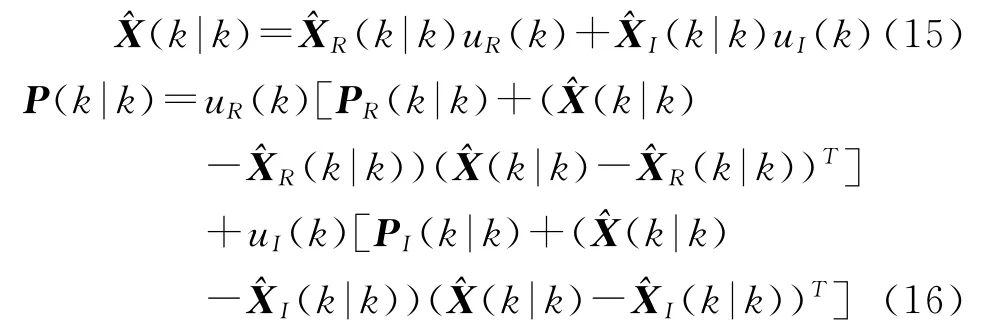
4 仿真分析

采用双红外和雷达对机动目标跟踪，采样间隔均为1s，在公共直角坐标系中的位置为（-10km，0，0）、（10km，0，0）、（0，0，0），噪声均方差为σrR＝100m，σθR＝σφR＝0．5°，σθⅠ＝σφⅠ＝5mrad。目标跟踪的精度指标Ⅰndex＝400，高门限TH＝λHⅠndex＝0．8Ⅰndex，低门限TL＝λLⅠndex＝0．6Ⅰndex。目标在空中做等高机动：0s～20s匀速运动，20s～90s匀加速运动，90s～130s匀减速运动，130s～316s匀速转弯，316s～386s匀加速运动。为了提高计算效率，粒子的个数n＝30。λH和λL分别表示高、低门限因子，雷达开机时间占总跟踪时间比值用ton表示，PF次数占总滤波次数比值用n＿pf表示。

图2 Radar／IF联合跟踪示意图

图3 在XY 方向和Z 方向上的跟踪示意图

图4 雷达辐射时间图

图5 仿真100次后均方误差分布图

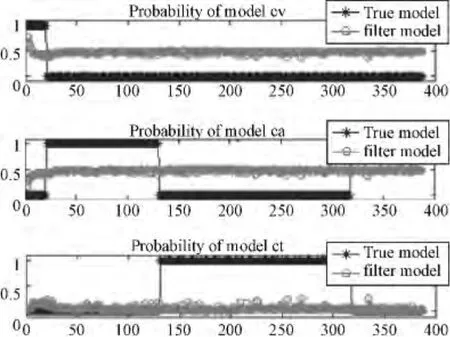
图6 模型概率示意图

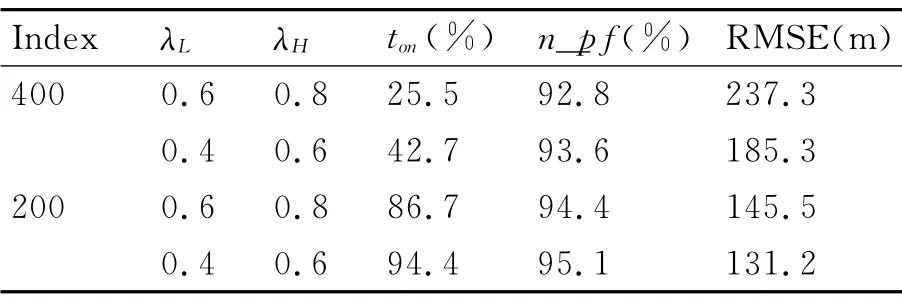
表1 不同精度指标、不同门限下雷达开机时间，粒子滤波时间，跟踪误差变化表

从图3～图6和表1可以看出：

1）提出的双门限自适应滤波算法能根据高门限与跟踪误差的大小控制雷达开关机，根据低门限与跟踪误差的大小选择不同的滤波算法，从而形成了一个闭环控制回路。

2）算法在XY、Z方向上是收敛的，不会出现发散的情况，能对机动目标稳定的跟踪。当目标远离传感器时跟踪误差变大，此时雷达开机时间变长；当目标机动时，交互式多模型算法能自动调整各个模型的概率，从而能稳定地跟踪目标。

3）同一精度指标下，若门限值越小，则雷达开机时间越长、PF 次数越多，目标跟踪精度越高；若精度指标越高，则雷达开机时间越长，跟踪精度相应的越高，因此，可依据实际情况选择精度指标和高、低门限值。

5 结语

本文提出的两层交互式自适应滤波算法，具有：1）根据实际背景选择不同的跟踪精度指标，既能解决远距离的空对空或空对地打击，又能解决近距离的火炮打击。2）根据实际需求选择不同的高低门限，可实现雷达、红外对目标不同的跟踪形式，如：λH＝0，此时为雷达、红外联合跟踪；λH＝∞，红外对目标单独跟踪，可用于红外远程预警；λL＝0，此时跟踪的实时性要求较高采用EKF 滤波，λL＝∞，此时跟踪精度要求较高，采用PF 滤波。因此该算法具有较大的实际意义，不仅具有跟踪机动目标的能力，而且能根据实际背景选择不同的跟踪形式。但对多目标跟踪问题还需进一步研究。

［1］Cui N Z，Xie W X，Yu X N，et al．Multi-sensor distributed extended Kalman filtering algorithm and its application to radar／IR target tracking［C］／／Proceedings of SPIE（S0277-786X），1997，3086：323-330．

［2］Blackman S S，Dempster R J，Roszkowski S H．IMM／MHT applications to radar and IR multi-target tracking［C］／／Proceedings of SPIE（S0277-786X），1997，3163：429-439．

［3］Yang G S，Dou L H，Chen J，et al．Synergy decision in the multi-target tracking based on IRST and intermittent-working radar［J］．Information Fusion（S1566-2535），2001，2（4）：243-250．

［4］张高煜，江水，梁继民，等．采用序贯滤波的红外／雷达机动目标跟踪［J］．控制理论与应用，2007，24（5）：811-815．

［5］王毅．一种新的雷达与红外传感器异平台数据融合方法［J］．激光与红外，2010，40（3）：325-329．

［6］Zhong Zhi-tong，Yang Xiu-ting．The Applications of Nonlinear Kalman Filters in Passive Tracking with Bearing-only Measurements［J］．Technical Acoustics，2008，27（6）：912-916．

［7］LIU Sheng，WANG Meng-jun，ZHANG Lan-yong．Research on Information Fusion of Infrared and Radar Sensor Based on SVM［C］／／Proceedings of 2012Inter national Conference on Measurement，Information and Control，MIC，2012：98-101．

［8］Wan E A，Van der Merwe R．The unscented Kalman filter for nonlinear estimation［C］／／Proceedings of the IEEE Symposium，2000：153-158．

［9］M Sanjeev rulampalam，Simon，Maskell，Neil Gordon，et al．A Tutorial on Particle Filters for Online Nonlinear／Non-Gaussian Bayesian acking［J］．IEEE Transactions on Signal Processing，2002，50（2）：174-188．

［10］S Arulampalam，B Ristic．Comparison of the Particle Filter with Range Parameterized and Modified Polar EKF for Angle-only Tracking［C］／／Proc．SPIE，2000，4048：288-299．

［11］Y．Bar-Shalomand，X．R．Li．Multitarget-Multisensor Tracking：Principles and Techniques［M］．Urbana，IL：YBS，1995．