间隙率对三轴向机织复合材料弹性性能的影响

白江波，熊峻江，高军鹏，益小苏

（1北京航空航天大学 交通科学与工程学院，北京100191；2北京航空材料研究院 先进复合材料国家重点实验室，北京100095）

先进复合材料由于具有高的比刚度和比强度，以及性能的可设计性，因此在减重需求迫切的航空航天领域正得到日益广泛的研究和应用[1］。纺织复合材料属于结构型材料，可根据工程应用需求，对其微观结构进行设计，从而实现材料的宏观性能指标。纺织复合材料的弹性性能参数对于复合材料结构设计非常关键，因此，国内外很多研究人员开展了这方面的工作[2－6］。王瑞等[3］利用细观力学的代表体积元法建立了用于预测平纹织物复合材料弹性模量的解析模型，分析了细观结构与宏观性能之间的关系，通过该方法预测结果与实验结果吻合良好。Xiong等[7，8］将平纹机织复合材料经纬两个方向弯曲的纤维束抽象为正弦曲梁模型，更加接近材料的真实构型，基于能量法预测了拉伸和压缩弹性模量，与实验结果吻合良好。Nguyen等[9］提出了一种预测碳纤维平纹机织复合材料剪切模量的解析模型，将纤维束简化梁单元，预测了织物的初始滑移区、弹性变形范围和剪切模量，与实验结果吻合良好。李典森等[10］在四步法方型三维机织复合材料细观结构单胞模型的基础上，将纱线横截简化为六边形面，建立了实体有限元模型，预测了材料的弹性常数，并分析了编织角和纤维体积含量对弹性常数的影响规律，预测结果与实验结果吻合良好。Chaphalkar等[11］基于经典层合板理论，提出了一种预测斜纹织物复合材料的拉伸和剪切模量的解析模型，预测结果与实验结果吻合良好。Kueh等[12］基于连续基尔霍夫板理论建立了单层三轴向机织复合材料的线弹性响应模型，通过横观各向同性的三维梁构建了单胞模型，利用有限元方法得到单胞的等效平板刚度矩阵（ABD矩阵），再利用刚度矩阵推算出面内拉伸、压缩和剪切等弹性性能，并与实验结果进行比较，二者吻合良好。Aoki等[13］采用与 Kueh等[12］类似的方法，基于有限元分析基础上建立了三轴向机织复合材料的半解析模型，区别在于Aoki等通过实体单元建模，预测了三点弯曲和纯弯曲的弹性性能，以及热膨胀系数，与实验结果吻合良好。Kueh等[14］进一步提出了三轴向机织复合材料超弹性应变能密度函数公式，该能量函数由基体、纤维束和相互作用三部分组成，表现出非线性的应力－应变响应，并且进行了实验验证，结果吻合良好。Zhao等[15］采用有限元和实验方法研究了三轴向机织复合材料承受单一拉伸载荷的渐进失效过程，分别采用最大应力准则、霍夫曼准则和蔡－吴准则预测了失效过程，与实验结果吻合良好。

从以上论述可知，已有文献针对纺织复合材料弹性性能开展了解析、有限元和实验方法的研究。其中三轴向机织复合材料，由于由三个方向（0°，60°和120°）纤维束编织而成，可通过树脂预浸并固化，形成具有一定刚度的二维单层机织复合材料结构，因此，这种结构在宏观尺度上的力学性能表现为准各向同性，所以在超低面密度复合材料结构中有很大的应用潜力。本工作对三轴向机织复合材料首先进行了几何构型分析，在此基础上建立了拉伸／压缩和剪切的有限元分析模型，将有限元预测的结果与文献中的实验结果进行了对比，结果吻合良好，证明了模型的有效性，并且进一步研究了间隙率对三轴向机织复合材料弹性性能的影响，可为三轴向机织复合材料在工程应用中的超轻量化设计提供参考。

1 几何构型及基本参数

三轴向机织复合材料是由三个方向的纤维束编织而成。为便于对比分析和保证基本材料参数的可靠性，本工作分析时使用纤维束材料及其参数和几何构型形式与Kueh等[12］的研究报告一致，如表1和表2所示。所有模型中丝束的宽度不变，即0.9mm，丝束的厚度为h。取出一个单胞（如图1所示），单胞边长分别为a和b，由中性轴组成的正六边形（虚线部分）特征边长为L，通过几何关系可知：

三轴向机织复合材料的间隙率k定义为单胞间隙面积比单胞总面积，可表示为

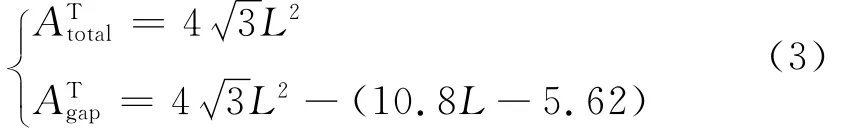
将式（3）代入式（2），可得

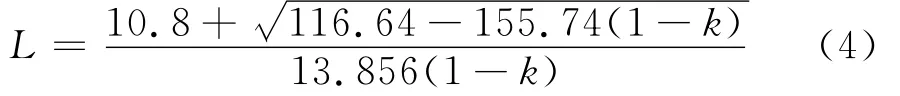
一个单胞的纤维面密度为

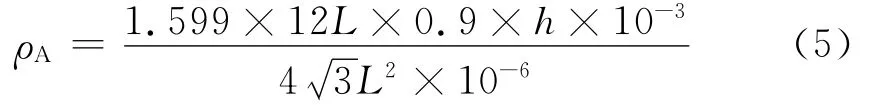
表1 纤维与基体材料性能Table 1 Fibre and matrix properties

表2 纤维束材料性能Table 2 Tow material properties

图1 三轴向机织复合材料几何构型及单胞几何参数Fig.1 Geometry construction and basic parameters of TWF composites

将式（5）进一步整理，可得

将式（4）代入式（6），得

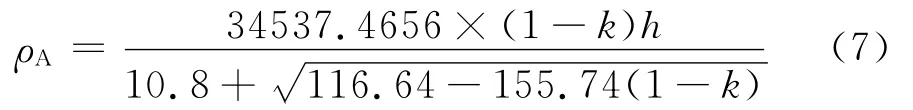
式（4）和式（7）建立了三轴向机织复合材料单胞中性轴组成的正六边形特征边长L和面密度ρA与间隙率k之间的关系，在不同纤维束厚度下的关系如图2厚度时面密度与间隙率之间的关系，同时需要指出当丝束宽度一定，最小间隙率极限值为1／3，即间隙率的取值范围为k∈（1／3，1），这是由三轴向机织复合材料的几何构型决定的。

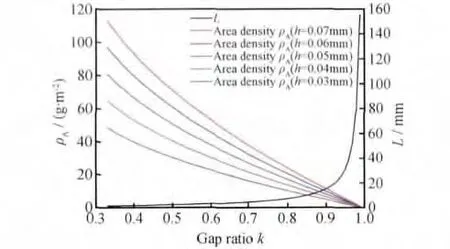
图2 面密度ρA与边长L随间隙率k的变化Fig.2 Surface densityρAand feature length Lwith increase of gap ratio k

2 计算模型及有效性验证

2.1 计算模型

在前面的几何构型的基础之上，采用有限元方法研究了间隙率改变时对三轴向机织复合材料的拉伸刚度、压缩刚度、剪切刚度和泊松比等面内弹性性能和比刚度的影响，采用商用软件ANSYS中的实体单元进行建模和分析。

为了尽可能减少边界条件对分析结果的影响，所有分析模型均采用三胞模型（如图3所示）。对于0°拉伸／压缩模型（如图3（a）所示）：约束端约束x向自由度，并且在约束端选择一个关键点约束所有自由度；在加载端施加位移载荷ux；计算分析后可得到约束端的支反力合力Fx及y向位移uy。0°拉伸／压缩刚度和泊松比可表示为

式（8）中为区别拉伸和压缩刚度，Stx和Scx分别表示拉伸和压缩刚度；比刚度只需用相应刚度除以面密度即可。

对于90°拉伸／压缩模型（如图3（b）所示）：约束端约束y向自由度，并且在约束端选择一个关键点约束所有自由度；在加载端施加位移载荷uy；计算分析后可得到约束端的支反力合力Fy及x向位移ux。90°拉伸／压缩刚度表示为

式（9）中为区别拉伸和压缩刚度，Sty和Scy分别表示拉伸和压缩刚度；比刚度只需用相应刚度除以面密度即可。

图3 有限元模型 （a）拉伸模型；（b）压缩模型；（c）剪切模型Fig.3 FEA models （a）tension／compression model of 0°direction；（b）tension／compression model of 90°direction；（c）tear model

对于剪切模型（如图3（c）所示）：约束端约束全部自由度，加载端（三个端面）先分别进行节点耦合，形成刚性端面，在大加载端面约束所有转动自由度和z向自由度并在中心耦合节点施加一个y向力Ty，在两个小端面分别施加一对相反的x向力Tx，可形成剪切受力状态，根据力矩平衡可得

将式（1）代入式（10）中，可得

计算分析后可得到大加载端在y向位移uy，剪切应变可近似表示为

剪切刚度可表示为

将式（12）代入式（13）中，可得

2.2 有效性验证

为了验证上述模型的有效性，根据Kueh等[12］的研究报告几何参数（纤维束宽度为0.9mm，厚度为0.07mm；纤维束之间搭接比较致密，三角形间隙非常小）和材料参数（如表1和表2所示）建模，并且与他们实验测定的结果进行了对比。由于三轴向机织复合材料一定会存在三角形的间隙（如图4所示），只有当完全没有三角形的间隙时它的间隙率k才为1／3，但实际情况下这是不可能的，所以建模时将k取0.34来进行近似。各刚度分析模型的变形位移云图如图5所示，有限元分析结果与Kueh等[12］的研究报告的实验结果对比情况如表3所示，由表3可知，有限元分析与实验吻合的很好，证明前面建立的分析模型是有效的。

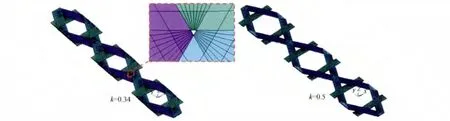
图4 三轴向机织复合材料三胞模型Fig.4 Three representative unit cell model of TWF

表3 预测与实验结果Table 3 Predicted and measured results

3 间隙率对弹性性能的影响

在前面2.2节证明了分析模型的有效性之后，下面进一步分析三轴向机织复合材料的面内刚度随间隙率的变化。仍然使用Kueh等[12］的研究报告中的材料参数，纤维束宽度固定为0.9mm，厚度固定为0.06mm。图7至图12给出了0°和90°方向拉伸／压缩刚度、剪切刚度和泊松比以及比刚度随间隙率k的变化，图6给出了当h＝0.06，k＝0.5时，各刚度分析模型的变形位移云图，可知：（1）0°方向拉伸刚度和压缩刚度相等，90°方向拉伸刚度和压缩刚度也相等；（2）0°和90°方向拉伸／压缩刚度以及剪切刚度随k的增加而减小，泊松比随k的增加略微增加（几乎不变）；（3）0°方向比拉伸／压缩刚度随k的增加而略微增加，90°方向比拉伸／压缩刚度随k的增加而略微减小，比剪切刚度随k的增加几乎不变。

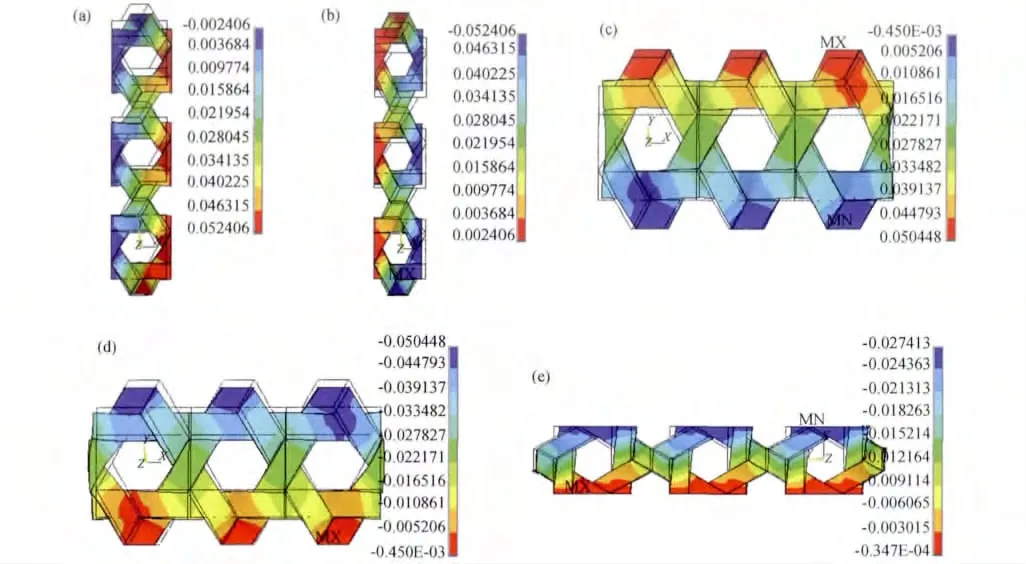
图5 当h＝0.07且k＝0.34时各刚度分析模型的变形位移云图（a）0°方向拉伸变形；（b）0°方向压缩变形；（c）90°方向拉伸变形；（d）90°方向压缩变形；（e）剪切变形Fig.5 Deformation distribution of stiffness analysis models with h＝0.07and k＝0.34（a）tension deformation of 0°diretion；（b）compression deformation of 0°diretion；（c）tension deformation of 90°diretion；（d）compression deformation of 90°diretion；（e）tear deformation

图6 当h＝0.06且k＝0.5时各刚度分析模型的变形位移云图（a）0°方向拉伸变形；（b）0°方向压缩变形；（c）90°方向拉伸变形；（d）90°方向压缩变形；（e）剪切变形Fig.6 Deformation distribution of stiffness analysis models with h＝0.06and k＝0.5（a）tension deformation of 0°direction；（b）compression deformation of 0°direction；（c）tension deformation of 90°direction；（d）compression deformation of 90°direction；（e）tear deformation

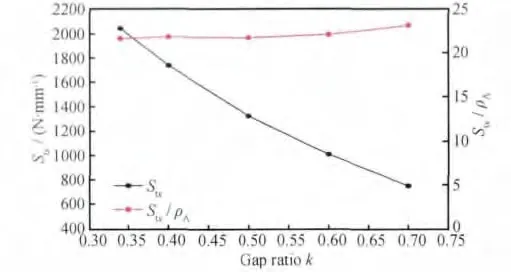
图7 0°方向拉伸刚度St x与比刚度St x／ρA随间隙率k的变化Fig.7 Tension stiffness of 0°direction St xand specific stiffness St x／ρAwith increase of gap ratio k

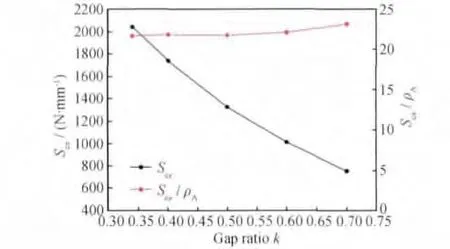
图8 0°方向压缩刚度Scx与比刚度Scx／ρA随间隙率k的变化Fig.8 Compression stiffness of 0°direction Scxand specific stiffness Scx／ρAwith increase of gap ratio k

图9 90°方向拉伸刚度Sty与比刚度Sty／ρA随间隙率k的变化Fig.9 Tension stiffness of 90°direction Styand specific stiffness Sty／ρAwith increase of gap ratio k

图10 90°方向压缩刚度Scy与比刚度Scy／ρA随间隙率k的变化Fig.10 Compression stiffness of 90°direction Scyand specific stiffness Scy／ρAwith increase of gap ratio k

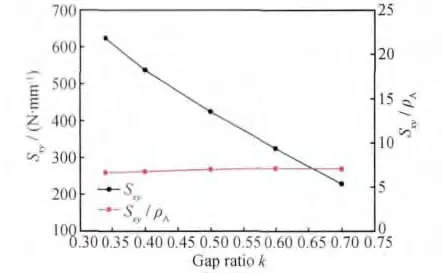
图11 剪切刚度Sxy与比刚度Sxy／ρA随间隙率k的变化Fig.11 Tear stiffness Sxyand specific stiffness Sxy／ρAwith increase of gap ratio k

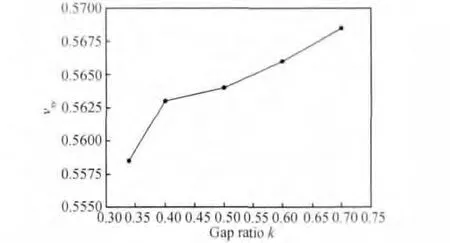
图12 泊松比νxy随间隙率k的变化Fig.12 Poisson′s ratioνxywith increase of gap ratio k

4 结论

（1）根据三轴向机织复合材料几何构型，建立了三轴向机织复合材料的面密度和单胞特征边长与间隙率之间的关系。

（2）建立了三轴向机织复合材料拉伸、压缩和剪切的有限元计算模型，并将预测的拉伸刚度、压缩刚度、剪切刚度和泊松比与实验结果进行了比较，吻合良好。

（3）分析了间隙率改变时对三轴向机织复合材料的拉伸刚度、压缩刚度、剪切刚度和泊松比和比刚度的影响，发现刚度随间隙率的增加而显著下降，而比刚度和泊松比随间隙率的增加变化较小。

[1]中国航空研究院.复合材料结构设计手册[M］.北京：航空工业出版社，2001.11.

[2]易洪雷，丁辛.三维机织复合材料的弹性性能预报模型[J］.力学学报，2003，35（5）：570－577.YI H L，DING X.A model to predict elastic properties of 3D woven composites[J］.Acta Mechanica Sinica，2003，35（5）：570－577.

[3]王瑞，王建坤，武玲.平纹织物复合材料的弹性模量预测[J］.复合材料学报，2002，19（1）：90－94.WANG R，WANG J K，WU L.Prediction for elastic properties of plain weave fabric composites[J］.Acta Materiae Composite Sinica，2002，19（1）：90－94.

[4]CALLUS P J，MOURITZ A P，BANNISTER M K，etal.Tensile properties and failure mechanisms of 3Dwoven GRP composites[J］.Composites：Part A，1999，30（11）：1277－1287.

[5]SHENG S Z，HOA S V.Three dimensional micro－mechanical modeling of woven fabric composites[J］.J Compos Mater，2003，37（9）：763－89.

[6]KING M J，JEARANAISILAWONG P，SOCRATE S.A continuum constitutive model for the mechanical behavior of woven fabrics[J］.International Journal of Solids and Structures，2005，42（13）：3867－3896.

[7]XIONG J J，SHENOI R A，CHENG X.A modified micromechanical curved beam analytical model to predict the tension modulus of 2Dplain weave fabric composites[J］.Composites：Part B，2009（40）：776－783.

[8]CHENG X，XIONG J J.A novel analytical model for predicting the compression modulus of 2DPWF composites[J］.Composite Structures，2009，88（2）：296－303.

[9]NGUYEN M，HERSZBERG I，PATON R.The shear properties of woven carbon fabric[J］.Composite Structures，1999，47（1－4）：767－779.

[10]李典森，卢子兴，蔺晓明，等.三维四向编织复合材料弹性性能的有限元预报[J］.北京航空航天大学学报，2006，32（7）：828－832.LI D S，LU Z X，LIN X M，etal.Finite element prediction of elastic properties of three dimensional and four directional braided composites[J］.Journal of Beijing University of Aeronautics and Astronautics，2006，32（7）：828－832.

[11]CHAPHALKAR P，KELKAR A.Classical laminate theory model for twill weave fabric composites[J］.Composites：Part A，2001，32（9）：1281－1289.

[12]KUEH A B H，PELLEGRINO S.Triaxial weave fabric composites[R］.European Space Contractor Report，Department of Engineering，University of Cambridge，30June 2007.

[13]AOKI T，YOSHIDA K，WATANABE A.Feasibility study of triaxially－woven fabric composite for deployable structures[C］／／48th AIAA／ASME／ASCE／AHS／ASC Structures，Structural Dynamics，and Materials Conference，23－26April 2007，Honolulu，Hawaii.AIAA 2007－1811.

[14]KUEH A B H.Fitting－free hyperelastic strain energy formulation for triaxial weave fabric composites[J］.Mechanics of Materials，2012，47（4）：11－23.

[15]ZHAO Q，HOA S V，OUELLETTE P.Progressive failure of triaxial woven fabric（TWF）composites with open holes[J］.Composite Structures，2004，65（3－4）：419－431.