陶瓷传感器烧结升温过程中温度场的有限元分析
2014-12-01杨雄艾中洲李小明长江大学机械工程学院湖北荆州434023
杨雄,艾中洲,李小明 (长江大学机械工程学院,湖北 荆州434023)
石油测井是石油工业技术中的基本环节。井下环境具有高温、高压的特点,地磁、地电等外界环境会产生较大干扰,导致一般材料的传感器在井下作业时不能精确测量井下的数据。陶瓷材料的耐高温性能极好,且具有优良的耐磨性和耐化学腐蚀,同时还是一种很好的电绝缘材料,能满足井下复杂工况的作业条件,所以陶瓷传感器在石油测井中具有广阔的应用前景[1]。然而由于陶瓷传感器为多孔、异型、多台阶的复杂结构,在烧结过程中容易产生裂纹而达不到使用要求。为此,笔者应用有限元软件Ansys模拟了测井陶瓷传感器烧结升温过程,分析不同的烧结曲线对陶瓷传感器坯体内部温度场的影响规律,以便为优化烧结工艺提出理论依据。
1 烧结过程分析的理论基础
1.1 非线性瞬态热传导问题的控制方程

式中,ρ为密度,kg/m3;c为比热,J/(kg·℃);T 为温度,℃;t为时间,s;qm为内部热生成率,W/m3;Kx、Ky、Kz分别为热传导系数,W/(m·℃);Γ为物体边界。
1.2 边界条件
目前应用较多的是第一类边界条件,即已知物体的表面温度,用热电偶所测定的窑炉内的温度、时间曲线表示坯体边界上的边界温度变化,用方程式表达如下[2]:

1.3 初始条件
初始条件是过程开始时物体整个区域中所具有的温度为已知值,其计算公式如下:

式中,T0为已知温度常数,℃,表示物体初始温度是均匀的;f(x,y,z)为已知函数,表示初始温度是不均匀的。
一般取陶瓷坯体的初始条件为烧成前的内部温度分布,烧成前陶瓷坯体的温度分布均匀且为常温。
2 三维有限元模型的建立
2.1 建立几何模型

图1 陶瓷传感器有限元网格模型
模拟烧结对象为石油测井陶瓷传感器,陶瓷成分为Al2O3。参照实物,运用Solidworks软件进行三维建模,另存为后缀为x_t的格式后导入Ansys软件进行分析。在Ansys软件中,SOLID 70单元每个节点具有一个自由度,可用于三维稳态或瞬态传热分析,应用该单元进行传热计算。有限元网格模型如图1所示。
2.2 确定材料性能参数
Al2O3陶瓷弹性模量为200GPa,泊松比为0.3,线膨胀系数为1.3×10-6m/ (m·℃)。Al2O3陶瓷热物性参数随温度变化而变化(见表1)。
2.3 施加温度载荷
已知窑炉内初始温度为30℃,陶瓷体初始温度为20℃,烧结最高温度为1200℃。为简化问题,假设陶瓷烧结过程中的热量传递方式为传导,不受辐射的影响。陶瓷制品在从入窑到最高烧成温度及冷却至出窑温度的过程中,温度相对于时间的变化过程称之为烧结曲线,是陶瓷烧结过程中重要的参数指标。在Ansys软件Convencation指令中输入烧结曲线方程,将温度载荷施加到模型上。烧结曲线可归纳为以下2类:①等斜率烧结曲线,即从20℃开始分别按照斜率为15°、30°、45°的烧结曲线加载 (见图2);②变斜率烧结曲线,是指在烧结过程中的不同阶段,其升、降温速率是不同的,有2种变化趋势,即切线斜率逐渐变大 (下凹)和切线斜率逐渐变小 (上凸)。等时间下的直线斜率及变斜率烧结曲线对比图如图3所示。

表1 Al2O3陶瓷材料热物性参数表

图2 等斜率烧结曲线对比图
3 升温过程中温度场的计算及结果分析
3.1 不同等斜率烧结曲线下温度场的分布
在升温阶段,升温至1200℃左右时不同烧结曲线下的温度分布云图如图4所示。由图4可知,最高温度集中在圆孔与圆孔之间的薄壁区域,而两端面中心区域温度值最低。这是由于在受到外界传热中陶瓷体厚壁升温比较慢,而薄壁区受热升温比较快,端面情况则相反。
在Ansys热分析后处理模块中,温度梯度表示单位长度内的温度变化速率,温度梯度越小表示受热时间越长,在相变过程中产生的残余应力就相对较小[3]。在升温结束阶段,3种烧结曲线下陶瓷坯体总体温度梯度分布云图如图5所示。记录各工艺条件下温度梯度最大值及最小值并绘制成图 (见图6)。由图6可知,随着温度曲线斜率的增加,即升温速率的变快,陶瓷坯体整体的温度梯度数值有增大的趋势,且切线斜率在一定范围内波动时 (约30°以前),温度梯度数值变化幅度较小,切线斜率超过30°后,随着斜率增加温度梯度数值有明显变大的趋势。升温速率过快,陶瓷坯体外部升到很高温度时,其气孔率下降致密度不断增加,而坯体内部由于温差较大,温度较低,烧结才刚刚开始,其膨胀和收缩程度不同,产生热应力,以致产生裂纹[4]。

图4 不同等斜率烧结曲线下的温度分布云图

图5 不同等斜率烧结曲线下的温度梯度分布云图
不同烧结曲线下达到烧结温度所需时间不同 (见图7)。如使用低斜率的烧结曲线 (具有较慢的烧结速率),虽然在一定程度上能够有效降低热应力,但升温速度过慢,烧结时间过长造成资源浪费,降低了生产效率,综合考虑,选取斜率30°烧结曲线较为合适。

图6 不同等斜率烧结曲线下的温度梯度数值大小分布图

图7 不同等斜率烧结曲线下达到烧结 温度所需时间
3.2 变斜率烧结曲线下的温度场的分布
将30°等斜率烧结曲线转化为变斜率烧结曲线并考察其对陶瓷烧结性能的影响。观察陶瓷传感器实物可知,裂纹主要出现在圆孔与圆孔之间的薄壁区域以及大小圆孔转角处。为了进一步了解坯体内部温度场的分布情况,选取垂直于薄壁区域中心且平行于陶瓷坯体前后两端的截面作为研究对象并进行温度场的分析,其截面及所选节点位置如图8所示。升温过程中,不同烧结曲线下截面温度梯度在1200s时分布云图如图9所示。

图8 截面及所选节点位置图
从陶瓷坯体中选取4个具有代表性的节点A、B、C、D,得到不同烧结曲线下温度梯度随时间变化曲线图 (见图10、11、12)。

图9 不同烧结曲线下1200s时截面温度梯度分布图

图10 上凸曲线下节点温度梯度随时间变化曲线图
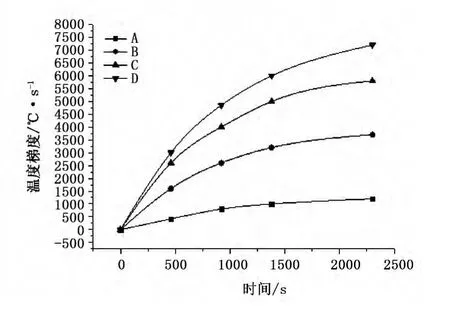
图11 等斜率曲线下节点温度梯度随时间变化曲线图
由图10、11、12可知,在3种烧结曲线下,在同一时刻节点A温度梯度数值始终最大,节点B、C次之,节点D温度梯度数值最小,这是由于陶瓷传感器坯体自身结构复杂,厚薄不一,薄壁区域传热快,而端面区域传热相对较慢。
在升温过程中,采用等斜率的烧结曲线,各节点温度梯度随时间有变大的趋势,且变大的速率趋于平缓;采用上凸烧结曲线,各节点温度梯度开始随时间有逐渐变大,达到一个最大值后温度梯度随时间逐渐减小;采用下凹烧结曲线各节点温度梯度随时间逐渐变大,且变化趋势越来越大。陶瓷烧结的终了时刻是升温过程中较重要的时间点,升温终了时陶瓷坯体的烧结状态会对后续的保温及冷却过程中坯体的性能产生很大影响。从数值上比较可知,采用上凸的烧结曲线,最大温度梯度为7000℃/m左右,小于等斜率曲线下的7200℃/m及下凹曲线下的11000℃/m。且在升温终了阶段,上凸曲线下温度梯度数值为3000℃/m,均远低于等斜率曲线和下凹烧结曲线下的数值。同时,上凸斜率的升温曲线,其初始阶段升温速率逐渐变大,能快速上升到较高温度,烧结至指定温度附近时温度值趋于稳定,故能有效降低烧结的温度梯度值,进而提高陶瓷传感器的烧结性能。
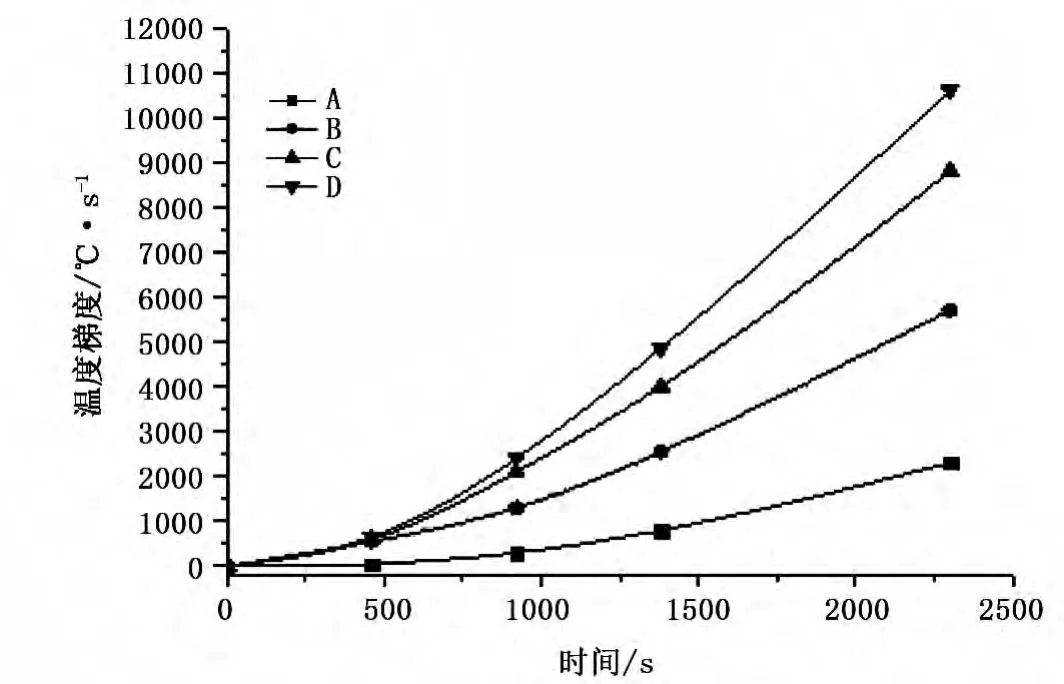
图12 下凹曲线下节点温度梯度随时间变化曲线图
4 结论
1)不同等斜率的温度曲线对陶瓷传感器烧结性能有显著影响,主要体现在采用斜率大 (即升温速率快)的烧结曲线能减少烧结时间,但会增加烧结过程中的温度梯度,降低陶瓷的烧结性能。综合考虑,采用30°的烧结曲线较为适宜。
2)变斜率的升温曲线会对陶瓷传感器烧结产生明显影响,采用上凸斜率的温度曲线能大大降低温度梯度,提高烧结性能。
[1] 杨清梅,孙建民 .传感器与测试技术 [M].哈尔滨:哈尔滨工业大学出版社,2004.
[2] 李建明,汪苏,袁胜华 .陶瓷烧成过程中温度场数值模拟及仿真 [J].中国陶瓷,2003,39(3):12-14.
[3] 周海球 .热分析技术在陶瓷材料烧结过程中的应用研究 [D].长沙:湖南大学,2012.
[4] Yung Ting-huang,Jin Huang.Effect of polarized electric field on piezoelectric cylinder vibratory gyroscope [J].Sensors,2006,128:248-256.
