一种基于前景理论和投影的区间数多属性决策方法
2014-12-01付沙李博宋丹湖南财政经济学院信息管理系湖南长沙410205
付沙,李博,宋丹 (湖南财政经济学院信息管理系,湖南 长沙410205)
多属性决策 (Multiple Attribute Decision Making,MADM)已成为现代决策科学的重要组成部分,目前主要运用在考虑多个属性的情形中,如何选择最佳备选方案或对方案排序的决策问题,该理论和方法已在工程、技术、经济、军事和管理等众多领域得到广泛应用。基于客观世界的复杂性和人们主观决策的不确定性等因素,容易导致决策信息的不确定性与不完备性,因此在实际的多准则决策问题中,决策者对某些准则的评价难以赋予一个确定的数值,而往往仅能给定一个取值范围,从而导致准则值以区间数的形式出现。文献 [1]针对决策者偏好信息和属性值均为区间数的多属性决策问题,对区间型多属性决策的心态指标法进行了较为详细的研究。文献 [2]探讨了属性值为区间数且已有方案偏好信息的多指标决策方法。文献 [3]提出区间数型模糊VIKOR方法,在决策过程中运用心态指标对区间数予以排序。
综合国内外研究文献,文献 [4]针对决策者所给期望信息的风险型混合多属性决策问题,提出了基于前景理论的决策分析方法。文献 [5]针对具有决策者期望的混合型多属性决策问题,提出了基于累积前景理论的决策分析方法。文献 [6]针对准则偏好值为区间数的不确定性决策问题,提出了基于前景理论的多准则决策方法。这一系列方法为解决带有决策者期望信息的多属性决策问题提供了较好的研究思路,但亦可发现该领域对属性值为区间数且权重信息不完全,同时还将决策者风险态度的多属性决策纳入考虑的研究相对较少。
通过对现有理论知识的综合探讨研究,笔者在区间数多属性决策中引入前景理论,提出基于该理论的区间数多属性决策方法,并通过算例分析验证该方法的有效性与合理性。
1 前景价值
Kahneman和Tversky给出了价值函数v的一种形式,它可以更好的满足决策者在面临收益时趋向于风险规避以及面临损失时趋向于风险追求的偏好特性[7]。Tversky等给出的价值函数为幂函数[8],具体表述为:

式中,Δx是表面价值的收益与损失,收益为正,损失为负;α和β分别表示收益和损失区域价值幂函数的凹凸程度,0<α<1,0<β<1,α和β愈大表明决策者越倾向于冒险;θ为损失规避系数,若θ>1,则决策者对损失更为敏感。Tversky等[9]认为,决策权重是决策者依据事件结果出现的概率p给出的某种主观判断,其函数π的表达如下:

前景价值由价值函数和决策权重函数共同决定,即:

2 区间数及其运算
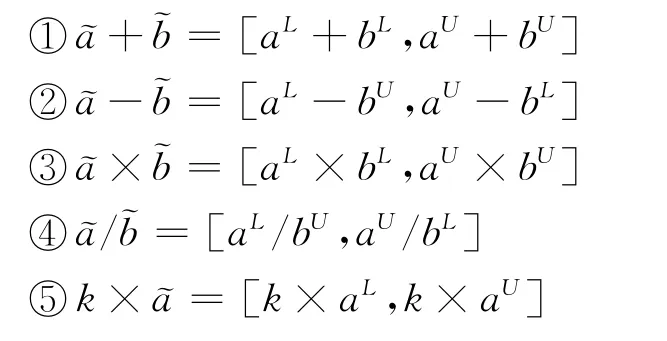
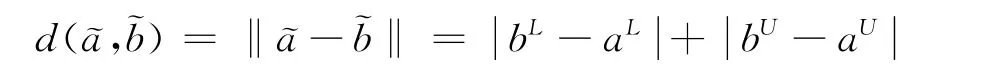

定义3[11]设和且则称:
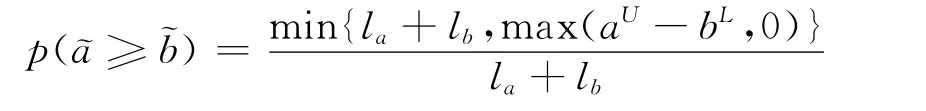
3 基于前景理论的区间数多属性决策方法
在研究多属性决策问题中,设有一个有限备选方案集A={A1,A2,…,Am}(m≥2),其中Ai表示第i个决策方案;属性集C={C1,C2,…,Cn}(n≥2),[fLij,fUij]表示第i个方案的第j个属性值,wj=[wLj,wUj]为各属性的权重。根据客观实际存在的或相关专家给出区间数决策矩阵,基于前景理论的区间数多属性决策方法对备选方案的属性值和各属性权重均采用区间数形式,可更好的解决如何判定客观事物的复杂性与不确定性等问题。
在各属性权重信息不完全且属性值为区间数的情况下,在区间数多属性决策中引入前景理论,提出基于该理论的区间数多属性决策方法,其具体步骤如下:
Step 1 给出各方案在各属性下的区间数评价值,构造区间数决策矩阵为消除各属性之间由于量纲不同而对决策结果所产生的影响,可运用区间数决策矩阵规范化的方法将区间数决策矩阵转化为规范化区间数决策矩阵表示第i个方案Ai对应于第j个属性Cj的区间数值结果。采用属性类型为效益型和成本型。
对于效益型属性,有:

对于成本型属性,有:
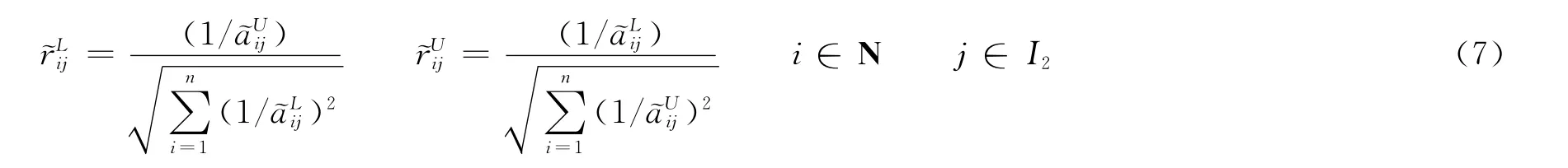
Step 2 前景理论的核心在于如何选取决策参照点,决策者在决策过程中将对照参照点来衡量收益或损失。分别选定正、负理想点作为参照点[12],规范化后决策矩阵的正、负理想方案分别为:

Step 3 计算各方案Ai到正、负理想方案的距离集。各方案Ai到正理想方案的距离集为:
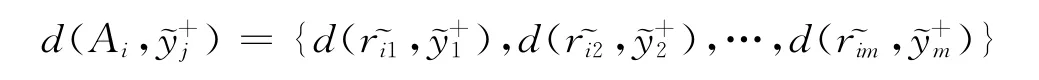
各方案Ai到负理想方案的距离集为:
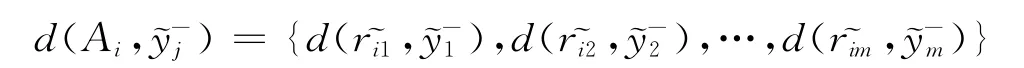
Step 5 针对属性权重信息不完全的情形,引入投影的思想[13],可得以下多目标规划模型,记做模型Ⅰ:
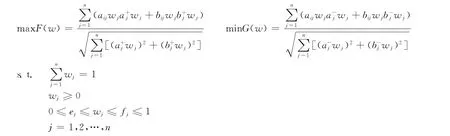
式中,ej、fj分别为权重值wj的下限与上限。若上述2目标的重要性程度一致,则模型Ⅰ可转化为如下的单目标规划模型,记做模型Ⅱ:

模型Ⅱ可通过Lingo与Visual C++混合编程仿真计算求得最优解,即得到满足目标函数max H(w)的属性权重清晰数w*=(w*1,w*2,w*3)[5]。
Step 6 根据所得各属性权重,计算各方案针对各属性收益与损失的决策权重函数:

式中,π+(wj)和π-(wj)各表示收益与损失的非线性权重函数;r和δ各表示收益与损失的决策权重函数的弯曲程序。
Step 7 计算各方案的综合前景值,依据其大小将方案予以排序为:

4 算例分析
某企业根据信息化建设的需要,拟定5个备选采购方案(A1,A2,A3,A4,A5),主要评价指标(属性)有3个(C1,C2,C3),其中C1代表产品价格,C2代表产品性能,C3代表售后服务。评估专家对5个备选方案进行评估,其数据整理后如表1所示。
在上述属性中,C1为成本型属性,C2、C3为效益型属性。已知的各属性权重信息:w=(w1,w2,w3),在不完全信息下各属性权重范围大致为:0.3≤w1≤0.5,0.25≤w2≤0.55,0.17≤w3≤0.23[14];且
1)依据式 (6)、(7),构建规范化区间数决策矩阵,如表2所示。
表1 区间数决策矩阵

表1 区间数决策矩阵
C1 C2 C3 A1 [1750,1840] [6.47,6.49] [7.36,7.56]A2 [2060,2250] [8.23,8.92] [7.28,7.64]A3 [1950,2040] [8.19,8.83] [8.85,9.24]A4 [1810,1900] [8.04,8.49] [7.65,7.89]A5 [2140,2200] [7.53,8.74] [8.04,8.44]
表2 规范化区间数决策矩阵
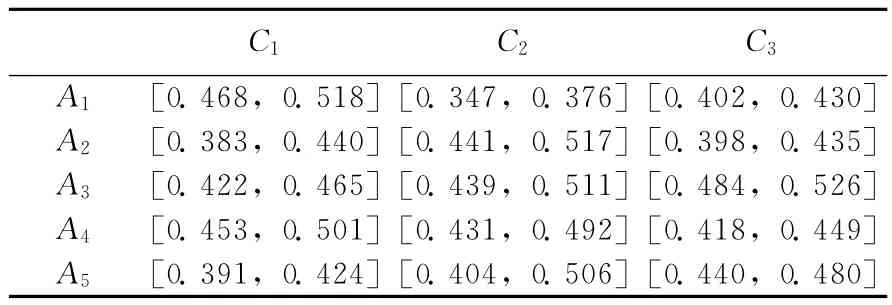
表2 规范化区间数决策矩阵
C1 C2 C3 A1 [0.468,0.518][0.347,0.376][0.402,0.430]A2 [0.383,0.440][0.441,0.517][0.398,0.435]A3 [0.422,0.465][0.439,0.511][0.484,0.526]A4 [0.453,0.501][0.431,0.492][0.418,0.449]A5 [0.391,0.424][0.404,0.506][0.440,0.480]

表3 正负理想方案
2)按照式 (8)、(9)计算规范化区间数决策矩阵的正、负理想方案,如表3所示。
3)按照Step 3计算各方案Ai到正、负理想方案的距离集,如表4、表5所示。
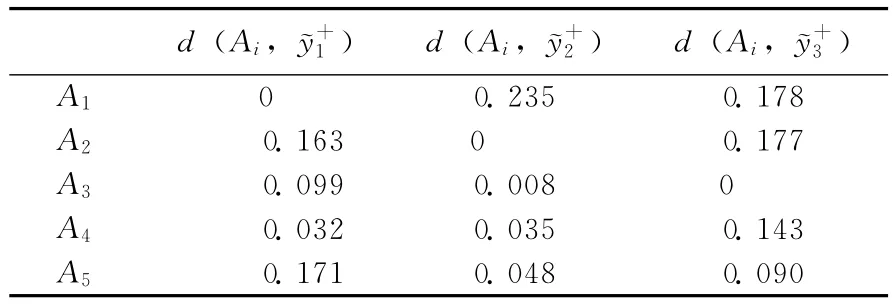
表4 各方案到正理想方案的距离集
4)由Step 4计算各方案在各属性下的正、负前景值。α、β和θ的取值可采用文献[12]中的数据,即α=β=0.8,θ=2.5。则正、负前景值分别为:
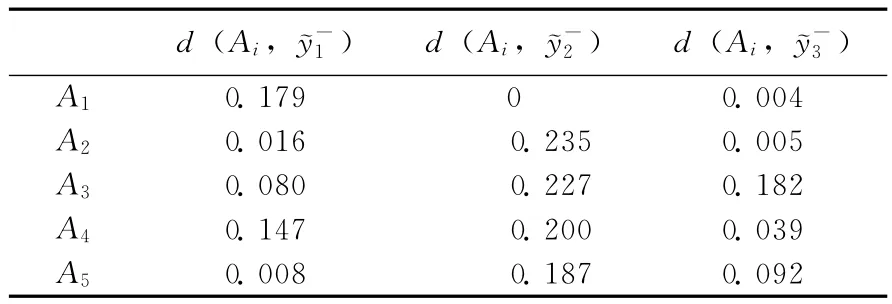
表5 各方案到负理想方案的距离集

表6 决策权重函数

5)将表2、表3中的数据代入模型Ⅱ,得到如下数学规划模型为:

通过Lingo与Visual C++混合编程求解该模型,得到满足该模型的目标函数值为:max H(w)=0.003394。同时,得到各属性权重清晰数为:
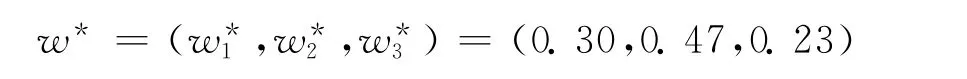
6)由式(11)计算各方案的决策权重函数,取r=0.61,δ=0.69,结果如表6所示。
7)由式(12),计算各方案的综合前景值为:
Vi=(V1,V2,V3,V4,V5)=(-0.4334,-0.2237,0.0858,-0.0726,-0.2429)最后,依据各方案的综合前景值,得到其排序结果为A3>A4>A2>A5>A1。经计算分析,笔者所得的结果与文献 [3]完全一致,证明此方法是可行与有效的,且由计算分析的步骤与过程可看出,该方法相比同类文献所提出的方法更具合理性。
5 结语
根据前景理论的思想,将决策者对各属性的正、负理想点作为参照点,给出针对区间数形式属性值的收益与损失计算方法,通过计算各方案的综合前景值以对其进行排序。在属性权重的确定上引入投影的思想,建立多目标规划模型以得到相应的权重。笔者所提的决策方法概念清晰、计算过程简单且适用面广,具备良好的推广应用与实际决策价值。最后,笔者例举典型的多属性决策问题——信息化建设中产品的采购决择,验证了该方的可行性与有效性,为解决考虑决策者心理行为的决策问题 (如采购决策、项目选择等问题)提供了一种更为有效的决策方法与思路。
[1] 万树平 .区间型多属性决策的心态指标法 [J].控制与决策,2009(1):39-43.
[2] 姜艳萍,樊治平 .给出方案偏好信息的区间数多指标决策方法 [J].系统工程与电子技术,2005,27(2):250-252.
[3] 孙红霞,张强 .区间数型模糊VIKOR方法 [J].模糊系统与数学,2011,25(5):122-128.
[4] 张晓,樊治平 .基于前景理论的风险型混合多属性决策方法 [J].系统工程学报,2012,27(6):772-781.
[5] 樊治平,陈发动,张晓 .基于累积前景理论的混合型多属性决策方法 [J].系统工程学报,2012,27(3):295-301.
[6] 胡军华,许琦 .基于前景理论的区间数多准则决策方法 [J].统计与信息论坛,2011,26(9):23-27.
[7] 李庆胜,刘思峰,方志耕 .基于前景理论的随机多属性VIKOR决策方法 [J].计算机工程与应用,2012,48(30):1-4,32.
[8] 马健,孙秀霞,郭创 .基于风险-效益比和前景理论的风险性多属性决策方法 [J].系统工程与电子技术,2011,33(11):2434-2439.
[9] Amos T,Kahneman D.Advances in prospect theory:Cumulative representation of uncertainty [J].J of Risk and Uncertainty,1992,5 (4):297-323.
[10] 苏志欣,王理,夏国平 .区间数动态多属性决策的VIKOR扩展方法 [J].控制与决策,2010,25(6):836-840,846.
[11] 任剑,高阳 .基于区间运算的随机多准则决策方法 [J].系统工程与电子技术,2010,32(2):308-312.
[12] 余德建,吴应宇,贺小容,等 .基于前景理论的信息不完全的区间型多属性决策方法 [J].软科学,2011,25(3):140-144.
[13] 徐泽水 .直觉模糊信息集成理论及应用 [M].北京:清华大学出版社,2008:10-80.
[14] 付沙,廖明华,肖叶枝 .模糊层次分析法在信息安全领域中的研究探索 [J].情报学报,2012,31(10):1105-1109.
