基于人工蜂群算法的负荷频率控制仿真研究

黄李健 （宁德师范学院物理与电气工程系，福建 宁德352100）

煤矿多区域互联电力系统中，负荷频率控制的主要目的是使系统工作频率和联络线功率值保持稳定，但由于各区域的发电功率和负荷需求经常出现失衡，从而会导致出现频率偏差和联络线功率偏差等问题［1］。近年来许多学者对LFC智能控制的实现主要集中在利用不同算法对PI和PID控制器增益进行调节及控制［2－5］，这些方法只是针对控制器参数的单一目标进行了优化，对系统参数的多目标优化问题还有待进一步研究。对此，笔者提出了一种在频率偏差单位阶跃响应的调节时间和超调量之间获得最优的多目标优化实现方法，利用LAE性能指标对各个权重集的调节性能做出评价，实现了利用多目标函数对2个区域的PID控制器的增益进行同步调节过程。

1 人工蜂群算法

人工蜂群算法 （ABC算法）是一种基于群体智慧的开元启发式算法，该算法适用于解决多目标优化问题［6］。算法中蜂群可以分为雇佣蜂、观察蜂和侦查蜂3个群体。蜂群对目标的搜索主要有3个过程：雇佣蜂随机的寻找蜜源。蜜源的位置代表最优问题的可能解，蜜源花蜜的数量代表目标函数值，而目标函数值决定了问题解的优劣。通过概率选择，侦查蜂找到蜜源位置，目标函数值越大意味着侦查蜂搜索到的最好的蜜源概率越高。雇佣蜂利用贪婪选择方法不断更换蜜源位置，并将更换后的目标函数值跟现有的函数值相比较，若更换后得到的目标函数值高，则对蜜源位置和目标函数值进行更新，替代现有的数值。雇佣蜂和观察蜂是对蜜源进行开采，侦查蜂是侦查蜜源，尽量找到更多的蜜源。若经过连续循环搜索后，蜜源位置仍无变化，则放弃该蜜源。放弃蜜源由侦查蜂随机寻找的新蜜源加以取代，同时侦查蜂对新蜜源跟现有解进行比较并判断是否存在更优解，如果存在则更新蜜源位置和目标函数。

2 多目标优化

在负荷频率控制中，基本的ABC算法已实现了单目标函数问题，对多目标优化问题可以通过最简单且实用的加权和方法加以实现，通过加权和对ABC算法进行修正以实现LFC的多目标优化。加权和方法就是将多目标优化当作复合目标函数来处理，复合目标函数可以表示为：

式中，wi为正加权值。

对式（1）作最小化处理便可得到多目标最优解条件，由于笔者研究的目的是要对频率响应的超调量和调节时间达到最佳点，则只需考虑复合目标函数：

式中，F1＝ITAE；F2＝ITSE（ITAE和ITSE分别是时间乘绝对误差积分准则和时间乘平方误差积分准则）；w1和w2为分配的权重，满足w2＝1－w1，w1∈ ［0，1］。

为衡量合成目标函数的适度性，需要对目标函数做归一化处理，归一化公式为：

式中，fit′i为归一化适度值；fiti为目标函数适度值；fitoverall表示所有的适度值；为避免在归一化中出现零点，δ设为0.999。

3 系统研究

两区域互联再热火力发电系统多目标优化系统模型如果图1所示。

系统模型包括2个再热汽轮机，PID控制器1和PID控制器2。比例增益（Kp）、积分时间常数（Ti）和微分时间常数（Td）是取决于区域控制误差信号（ACEi，i＝1，2，…）的可调参数。控制器输出u1和u2表示为：

其中，控制器积分增益（Ki）和微分增益（Kd）分 别 为 Ki＝Kp／Ti和 Kd＝KpTd。

自动发电控制（AGC）主要目标控制是区域控制误差信号（ACE），其中包括频率偏差（Δf）和联络线功率偏差（ΔPtie）相关信息量，2个区域的ACE表达式分别为：

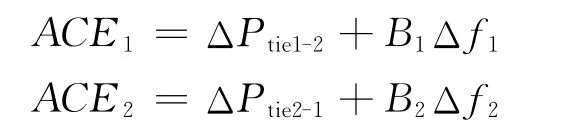
若各区域有负荷扰动出现，那么组合ACE信号将促使PID控制器对其进行误差补偿，控制器的主要作用就是调节ACE信号并尽快使误差为零。

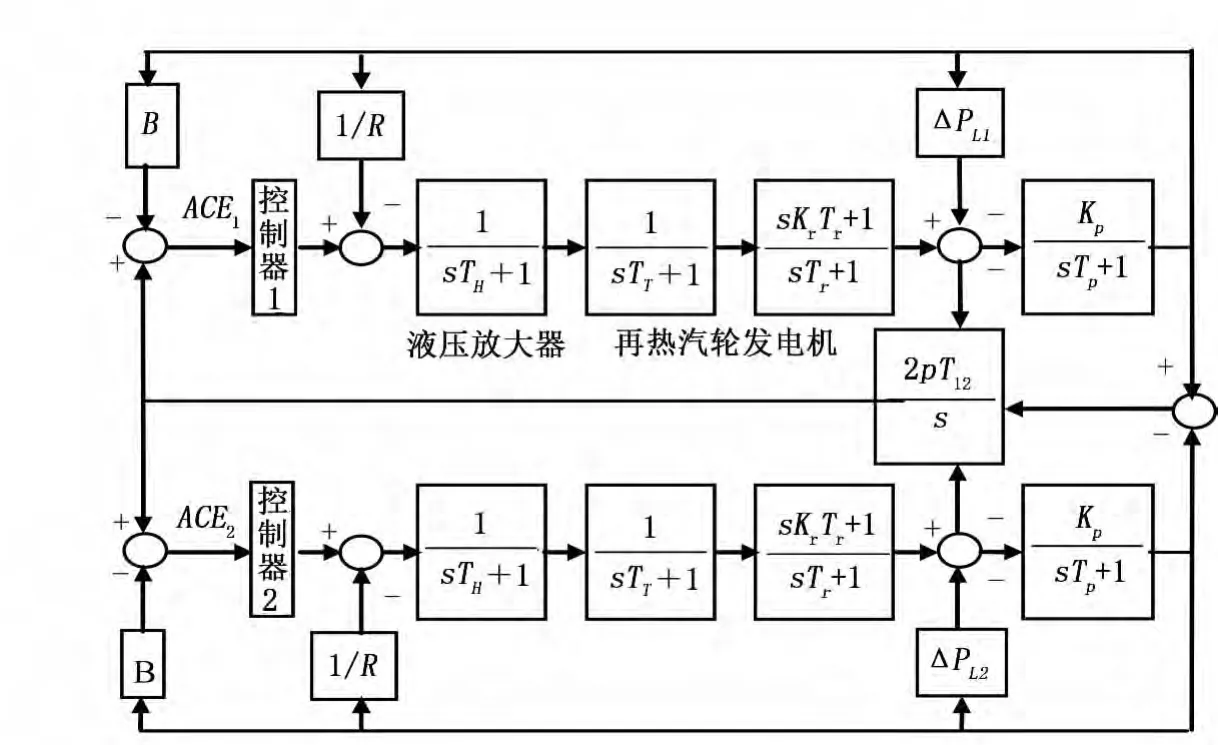
图1 两区域互联再热火力发电系统模型

4 目标函数

负荷频率控制的暂态闭环响应可以通过IAE，ISE，ITAE和ITSE误差准则来衡量（用系统实际输出与期望输出间偏差的某个函数的积分式表示的一种性能指标。性能指标是衡量控制系统性能优良度的一种尺度。对于单变量系统，常用的误差积分准则有绝对误差积分准则（IAE）、平方误差积分准则（ISE）、时间乘绝对误差积分准则（ITAE）和时间乘平方误差积分准则（ITSE）4种，不同的误差准则表示不同的系统性能和输出，所以用误差准则来表示目标函数。

负荷频率控制的暂态闭环响应可以通过IAE，ISE，ITAE和ITSE误差准则来衡量，各误差准则可以用以下各式表示：

自整定优化［7］是一种对控制器增益或参数做线程调度的方法，该方法鲁棒性较好并且容易实现。为满足系统变化的需要，控制器参数要连续可调并可用来对系统频率进行控制。控制器的输入为2个区域的ACE信号，对2个PID控制器同步优化算法过程如图2所示。

由图2可知，区域1的负荷扰动会对区域2的阶跃响应输出产生影响，反之亦然。因此，控制器同步优化会对2个区域起到适度控制调节的作用，文献［6－7］对该模型中PID在 ［0.2，2］范围内的参数调节做了详细论述，利用优化算法表达式：

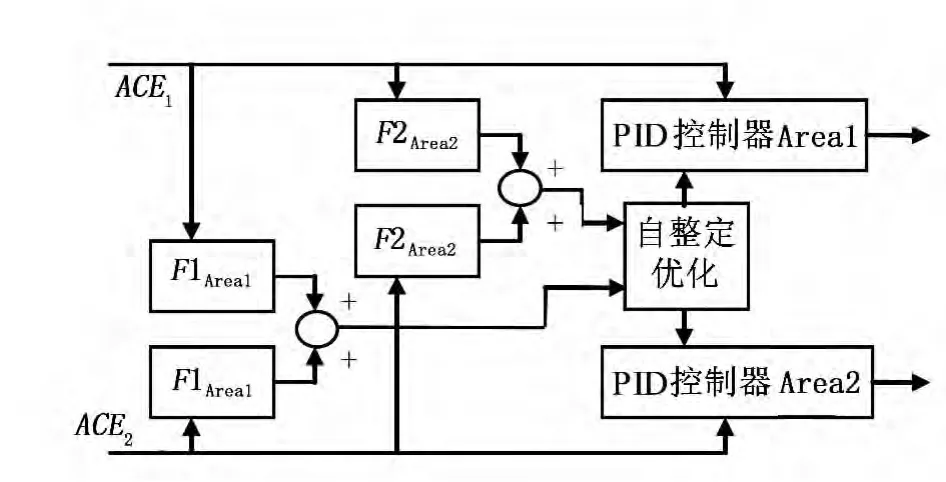
图2 同步优化过程

可对各区域的性能指标以加权和复合目标函数的形式对系统进行调节。

5 仿真结果

为了验证负荷频率控制中多目标加权和人工蜂群算法优化的有效性，通过对负荷需要变化利用Matlab进行了仿真试验，系统模型参数设置为f＝50Hz，TH1＝TH2＝0.08s，TT1＝TT2＝0.3s，Tr1＝Tr2＝10s，Tp1＝Tp2＝20s，Kp1＝Kp2＝120Hz／MW。

假设区域2中的负荷扰动为1%不变，在区域1中加入一个步长为25%的可变负荷扰动，其变化范围为±50%，通过改变负荷需求（ΔPL），观察系统性能的变化情况。设区域2中的额定负荷为0.01MW，权重集设为w1＝0.2，w2＝0.8，分别对区域1中各权重集、LAE性能优劣和两区域PID控制器做了同步调节试验，试验测试结果如表1和表2所示。

由表1可见，在区域1中负荷需求变化下的权重集w1＝0.2，w2＝0.8时具有最佳LAE特性；表2数据显示在负荷变化－50%时系统调节时间和超调量达到最小，说明负荷变化－50%时系统的鲁棒性最好。系统暂态响应仿真结果如图3～图5所示。

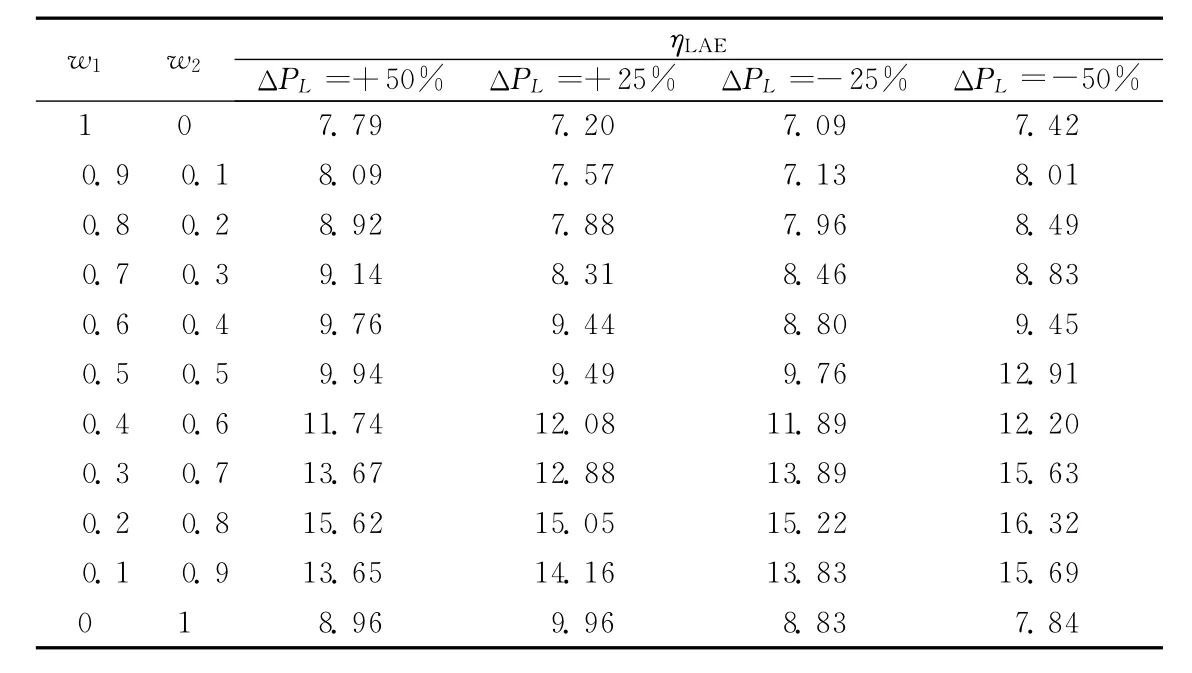
表1 不同负荷时的权重值及LAE性能

表2 不同负荷时的优化PID增益及系统性能

图3 不同负荷时的区域1频率偏差

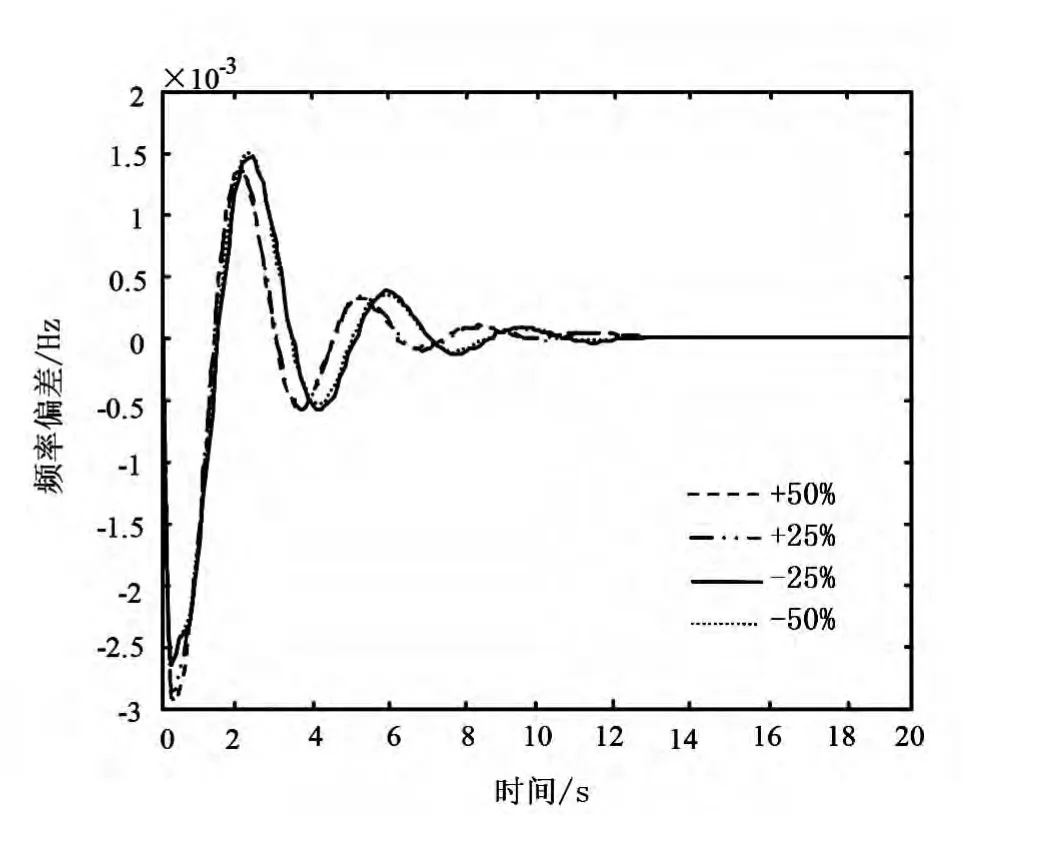
图4 不同负荷时的区域2频率偏差

从上述各图可见，区域1中，频率偏差阶跃响应随着负荷需求的改变而变化，－50%时的频率响应超调量比＋50%时的频率响应的超调量要低得多 （见图3）；在区域2中，当负荷需求的额定功率稳定在0.1MW时，频率偏差阶跃响应的变化量非常小 （如图4所示）；当区域1中的负荷小于区域2时，功率将从区域1传递至区域2，反之亦然 （如图5）。

6 结语

利用加权和多目标优化方法对煤矿负荷频率控制的PID控制器参数进行优化。通过人工蜂群算法对PID参数进行调整优化，对系统暂态响应的频率偏差、联络线功率偏差以及过渡时间和超调量等系统性能进行了分析和比较，结果表明基于加权和人工蜂群算法的PID控制器具有较好的鲁棒性。

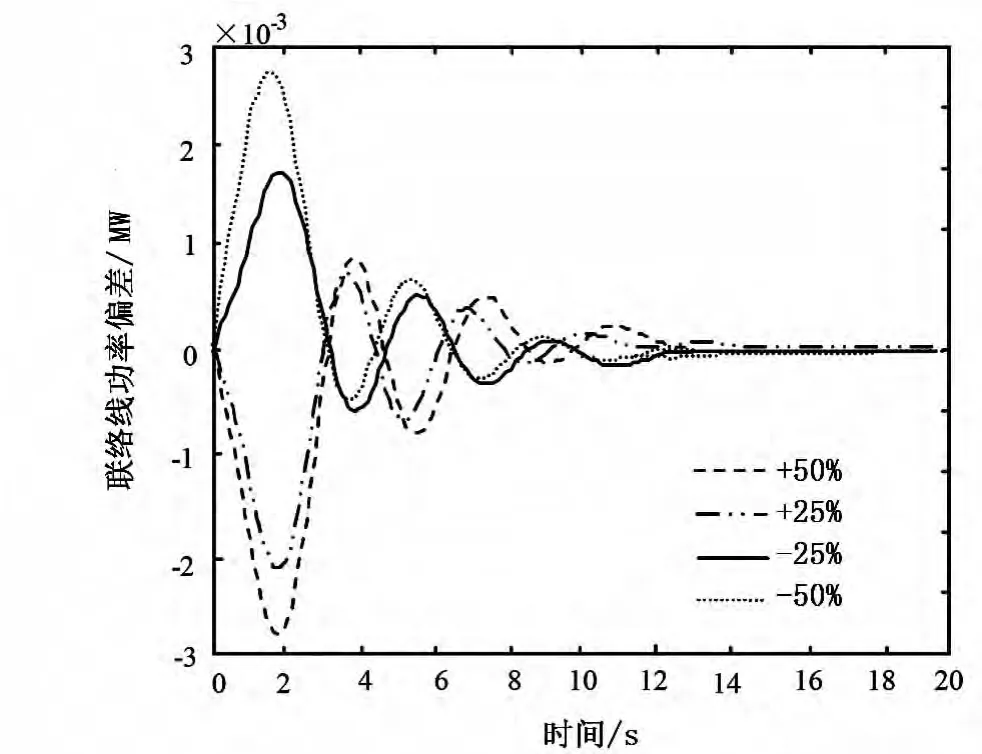
图5 不同负荷时的联络线功率偏差

［1］ Mcllwaine S A，Tindall C E，McClay W.Frequency tracking for power system control ［J］.IEE Proceedings C （Generation，Transmission and Distribution），IET Digital Library，1986，133 （2）：95－98.

［2］ 韦晓广，陈奎 .基于人工蜂群算法的电网故障诊断 ［J］.工矿自动化，2012，（11）：36－39.

［3］ 王海波，史友仁 .煤矿电力监控系统的研究与应用 ［J］.工矿自动化，2009，（7）：130－133.

［4］ Ali E S，Abd－Elazim S M.Bacteria foraging optimization algorithm based load frequency controller for interconnected power system ［J］.International Journal of Electrical Power ＆ Energy Systems，2011，33 （3）：633－638.

［5］ 米阳，吴晓，楚瀛，等 .基于滑模控制的单域电力系统负荷频率控制 ［J］.控制与决策，2012，27（12）：1881－1884.

［6］ Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization：artificial bee colony（ABC）algorithm ［J］.Journal of global optimization，2007，39 （3）：459－471.

［7］ Marler R T，Arora J S.The weighted sum method for multi－objective optimization：new insights ［J］.Structural and multidisciplinary optimization，2010，41 （6）：853－862.