机械碰撞振动系统分岔与混沌的参数演化

柴 林，吴晓明

（厦门大学物理与机电工程学院，福建 厦门361005）

碰撞振动是机械系统中常见的一种现象，其响应可能会呈现复杂的非线性混沌现象.在工程实际中，一方面，为了某种生产目的，可以利用碰撞振动的动力学原理设计制造如振动筛、压路机、微振造型机等多种冲击振动机械；另一方面，碰撞振动也可能造成负面影响，如降低稳定性、损坏设备、制造噪声等，特别是碰撞振动所产生的非线性运动是造成机械部件疲劳、损坏的主要原因之一［1］.因此，工程实际中要根据机械系统的功能需求去选择利用或者避免碰撞振动的非线性动力学现象.

碰撞振动是一个复杂的过程，它受多方面因素的影响，如碰撞体的约束状况、接触时的相对速度、接触面的几何形状及接触持续时间、局部塑性变形等，其研究涉及工程机械、系统动力学、数值分析等多个专业领域.牛顿、Poisson及 Whittaker理论构成了经典碰撞动力学理论的框架.在系统进行动态分析时，用于描述碰撞过程的模型有3种［2－3］：1）瞬时冲击模型；2）分段线性模型；3）考虑碰撞中的局部变形的模型，用Hertz接触理论描述接触力.

本文以一大类实际工程机械，如振动筛、制砖机、振动压实机为基础，建立了单自由度碰撞振动机械的通用动力学模型.采用瞬时冲击法，在碰撞过程中只考虑能量的损失，利用恢复系数法计算碰撞前后速度之间的关系，用四阶龙格——库塔法求解模型的动力学微分方程，讨论设计参数变化时系统呈现周期运动以及混沌现象的演化过程.

1 动力学模型及其运动方程

具有约束的单自由度碰撞振动系统的动力学模型如图1所示，质量为m的振子由刚度为k／2的线性弹簧和阻尼系数为c／2的阻尼器对称连接于支承台，振动台质量为M并受到振幅为A、频率为ω的强制简谐激励的作用，碰撞恢复系数设为R.

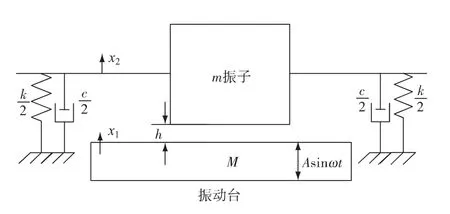
图1 单自由度碰撞振动系统的力学模型Fig.1 Mechanics model of SDOF collision vibration system

系统在未发生碰撞时，自由运动阶段方程为：

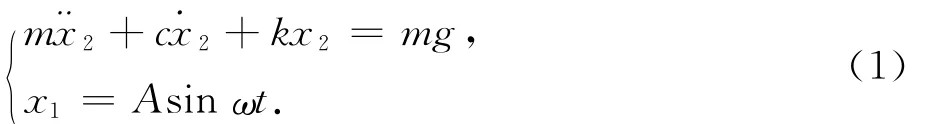
碰撞过程采用瞬时冲击模型，“－”、“＋”分别表示振动台与振子碰撞前后的瞬时状态，碰撞前后瞬时速度关系式为［4］：

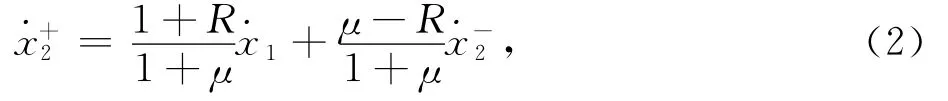
在MATLAB中用四阶龙格－库塔法求解二阶微分方程，并判断当x1＝x2时即发生碰撞，分别把这一时刻的速度值˙x－2和˙x1带入式（2）中，求出瞬时碰撞后下一时刻的速度.计算时，步长设置为ts＝0.000 1s，运行时间为4s.

已知参数有：m＝200kg，c＝11 000N·s／m，k＝500 000N／m，g＝10m／s2，A＝0.05m，h＝0.02m，R＝0.9，μ＝0.1，ω＝50×2π＝314.16rad／s，x2为位移，单位：m；dx2为速度，单位：m／s.

MATLAB运行结果如图2所示.从图2（a）、（b）可以看出振子作复杂的非周期运动，每一次碰撞结束后的一周期内速度和位移均无规律可言.由图2（c）可以看出，从相图得到运动状态是由多条不封闭曲线组成，而图2（d）上分布着多个离散的无规律的点，说明系统出现了混沌现象［5］.

2 参数对系统响应状态的影响

对于碰撞振动系统，设计参数的变化对系统是周期性响应还是混沌状态具有决定性影响，本节讨论碰撞振动系统设计参数对系统响应状态的影响.

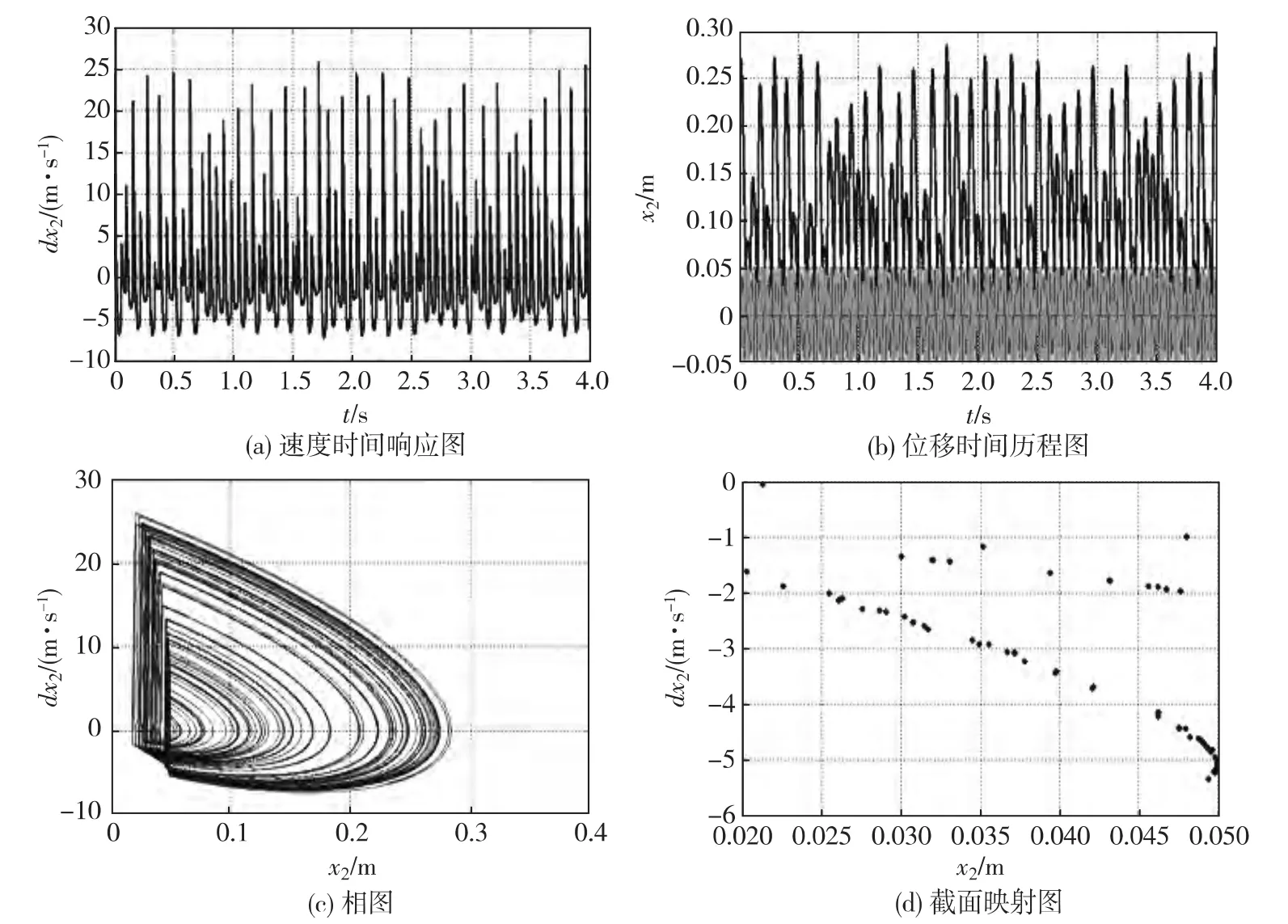
图2 系统动态响应Fig.2 Dynamics responses of system

2.1 初始碰撞位置

系统参数如上节所述，分别取初始碰撞位置h＝0.04m和h＝0.003m，数值仿真的位移和相图如图3所示，结合图2所示h＝0.02m时的系统响应图，可以看出系统运动状态表现出随机性和不可预测性，但同时振子的最大位移和整体运动趋势局限在一定范围内，显现出局部不稳定而整体稳定的特性［6－7］.在碰撞间隙为0～0.05m的范围内取值为0.003，0.02和0.04m的仿真数值结果表明，系统运动状态变化不大，碰撞间隙作为参数对系统的混沌现象产生和演化影响并不明显.

2.2 黏性阻尼系数

以阻尼系数为分岔参数，数值仿真系统的运动状态.通过计算，得到阻尼从4 000～18 000N·s／m，振子的状态变量全局分岔图（见图4），图中位置“一、二、三”分别对应参数阻尼c的值为9 280，10 290，11 610N·s／m.从图中可见，振子在“一”位置进入周期倍化阶段，此后系统从倍化分岔序列通向混沌，在“二”位置进入混沌运动状态，在“三”位置结束混沌运动状态.为此，我们分别选取c为10 000，10 500和16 000N·s／m进行动态响应数值计算，结果如图5所示.

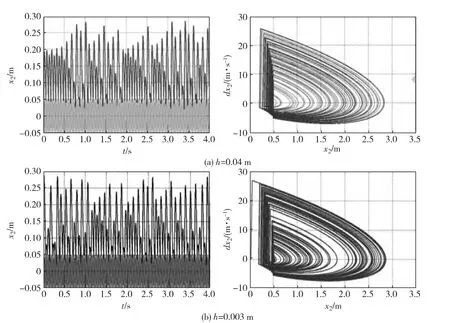
图3 不同初始碰撞位置的位移响应图（左）和相图（右）Fig.3 Displacement－velocity response graph（left）and phase portraits（right）（h＝0.04m、h＝0.003m）

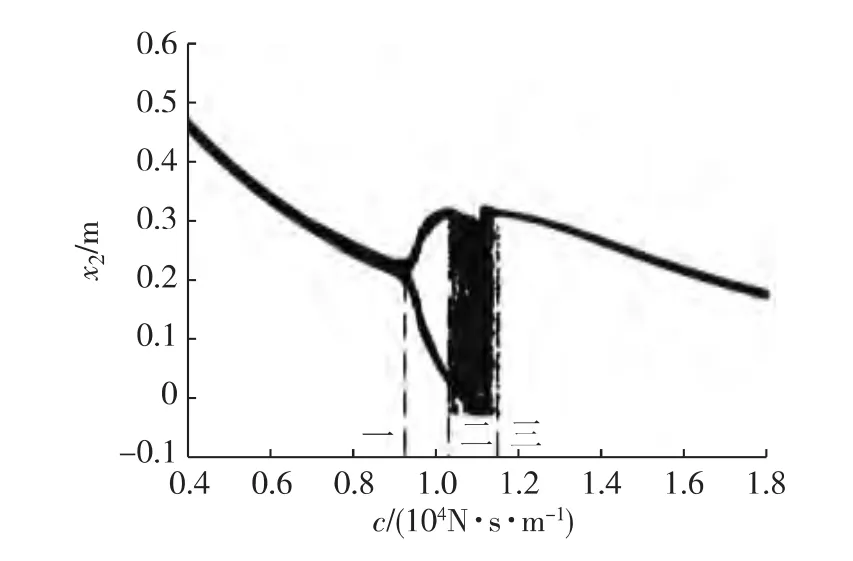
图4 阻尼c的全局分岔图Fig.4 Overall bifurcation of damp

从图5可看出，在阻尼c分别取10 000，10 500 N·s／m时，系统处于周期倍化运动状态和混沌状态.当阻尼c＝16 000N·s／m时，相图是一条闭合曲线，Poincaré截面映射图上表现为孤立的1个点，说明振子的响应呈现周期性，系统具有稳定的周期运动.

由阻尼变量全局分岔图4可见，碰撞振动系统的运动状态对振子支撑元件阻尼参数是敏感的，特别是在运动响应随阻尼变化发生分岔进而出现混沌状态的交界点“一”“二”“三”位置附近，阻尼常数的小变化会引起系统运动的极大变化.

2.3 刚度k

选定一组基本参数c＝6 000N·s／m，m＝200kg，A＝0.05m，ω＝314.16rad／s，取刚度k为变化参数，数值计算出关于参数k的全局和局部分岔图，如图6所示.

可见，刚度对系统响应周期的影响极大.随刚度增加，系统的运动状态变得复杂，混沌运动与周期运动、拟周期交错出现.从图6可看出，当k的数值从0.85×106N／m递增到0.95×106N／m 时，运动轨迹和周期性变得更为丰富，系统分别经历突变、倍化分岔、临界hopf分岔连接混沌区域.

2.4 激振频率ω

选定一组基本参数为m＝200kg，A＝0.05m，k＝500 000N／m，取激振频率ω为变化参数，计算出ω的系统全局分岔图，如图7所示.

从图7可得出，当阻尼系数一定时，随激振频率增加，振子的周期运动与非周期运动交替出现，且相邻周期与非周期的运动状态组合呈现一定规律性，并可看出周期运动和混沌区域的最高点逐渐增加；而随着阻尼系数c的递增，系统振子运动的最高位置明显减小，周期运动与混沌界限变得模糊，混沌区域增加.

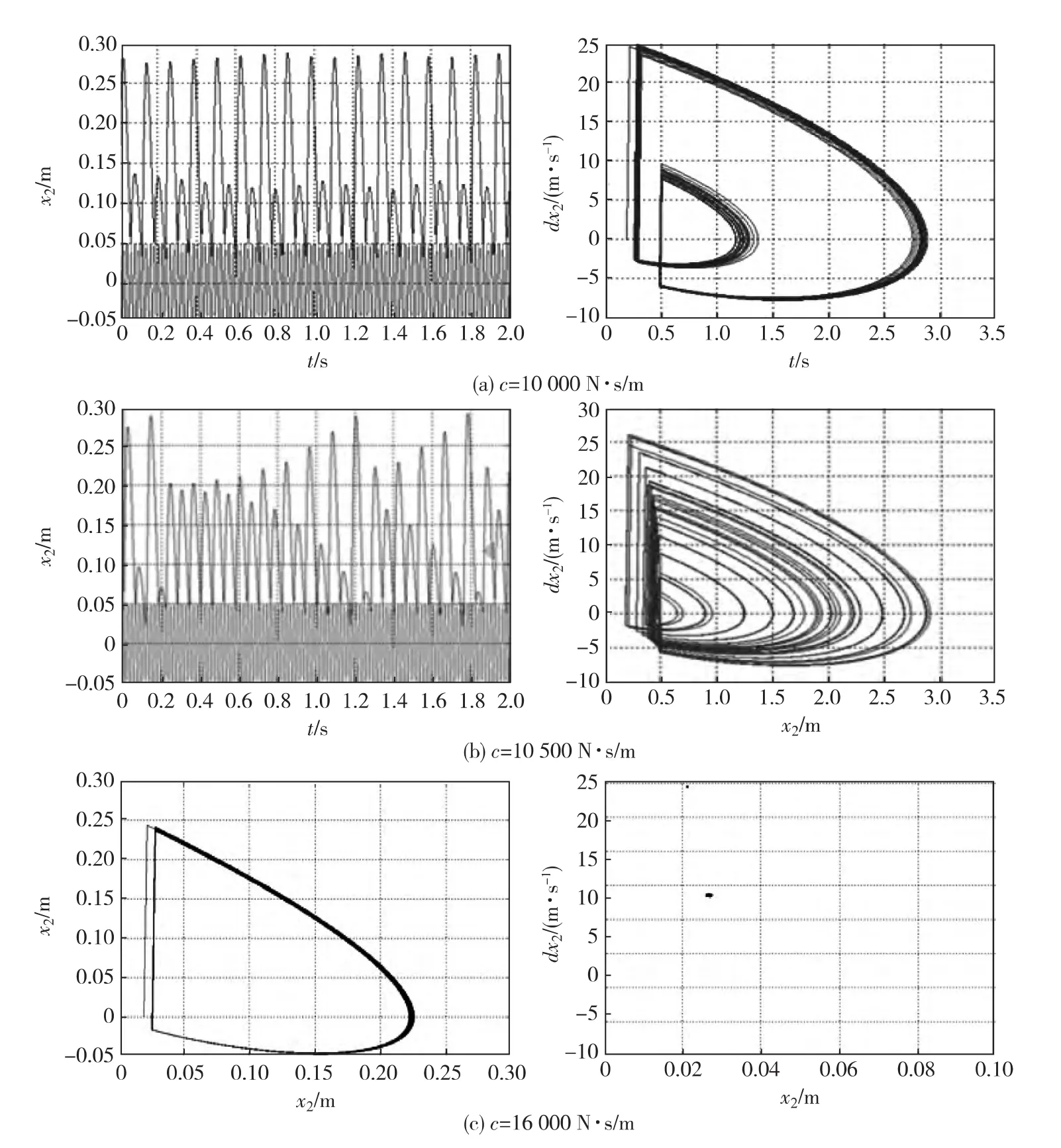
图5 不同阻尼c的系统动态相应数值仿真计算结果Fig.5 Displacement－velocity response and Phase portraits

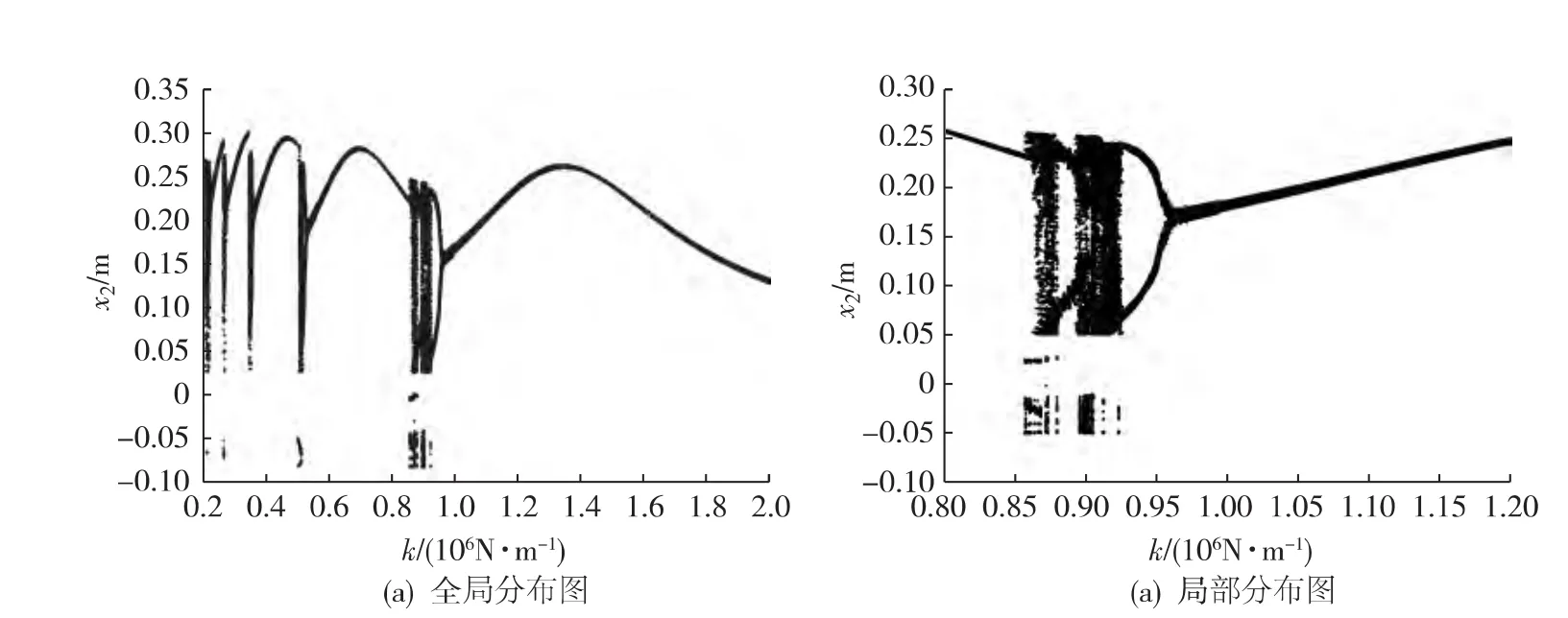
图6 刚度k的全局和局部分岔图Fig.6 Overall and part bifurcation of stiffness

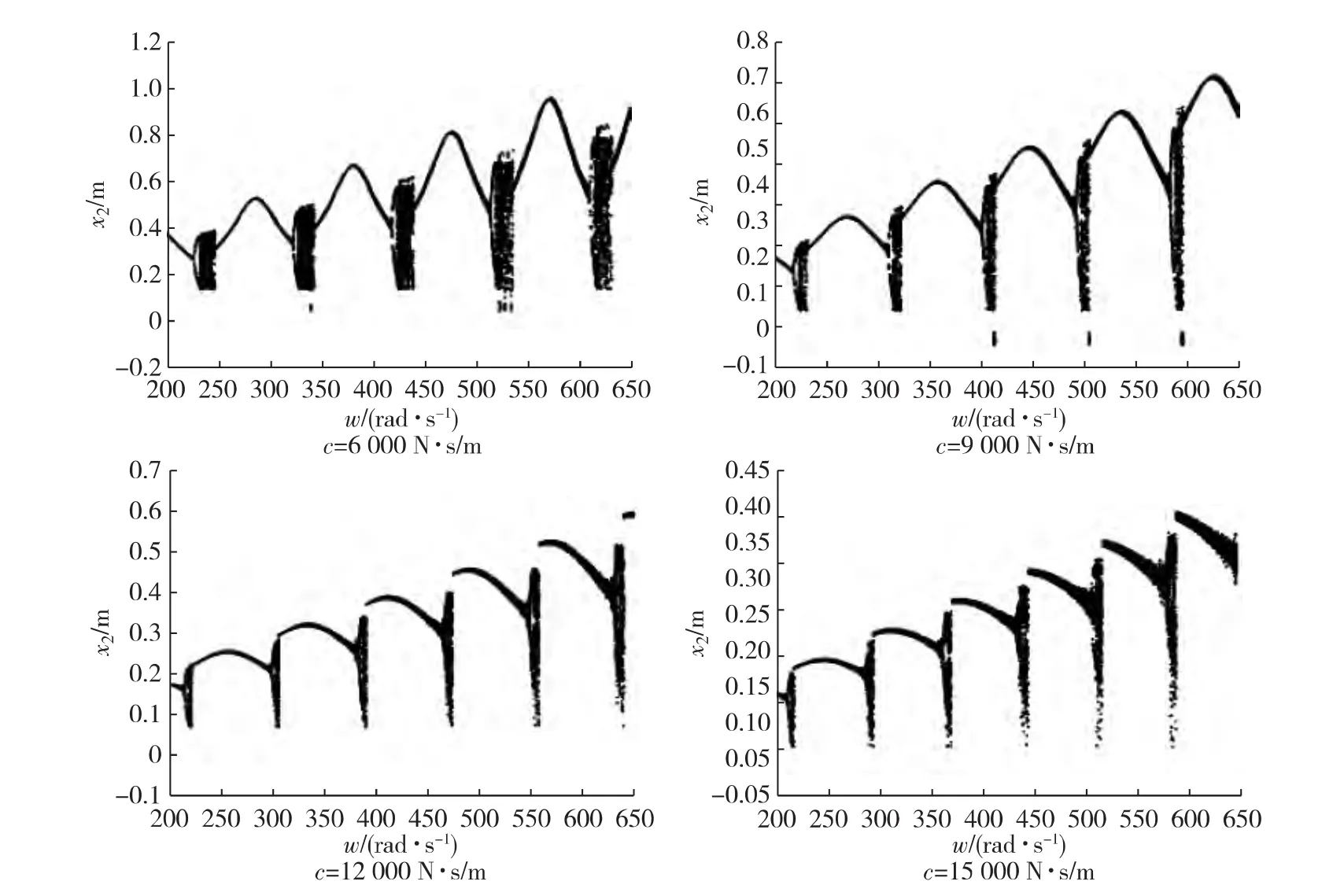
图7 频率ω的全局分岔图Fig.7 Overall bifurcation of frequency

3 典型设计参数的三维全局分岔图

系统分岔图是实际机械系统中设计参数选取的重要依据［8］.而典型设计参数往往是多元的，以台式制砖机为例，为了使振子运动达到理想工作状态，最常用的方法是改变支撑振子的弹簧和阻尼.由于二维分岔图每次只能选取单个设计参数，然后进行反复地样机试制实验，准确找到所需要的弹簧刚度和阻尼参数值并非易事.本文对力学模型的刚度和阻尼两个参数变化进行数值计算，得到系统刚度和阻尼在一定区间内变化的三维全局分岔图.

从图8可以得到，当阻尼c取6 000～14 000 N·s／m、刚度k从4.6×105N／m 递增到5.4×105N／m的区间中，振子在稳定单周期运动时位移最高点逐渐增大，而混沌区域逐渐减小，刚度k取4.6×105N／m时的系统混沌面积是取5.4×105N／m时的3倍左右.

4 结 论

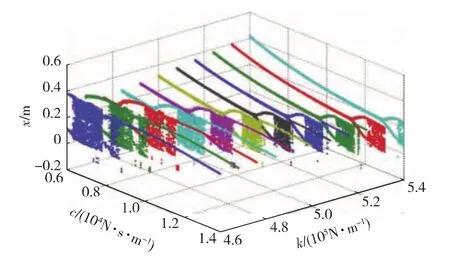
图8 分岔三维图Fig.8 Three－dimensional bifurcation

针对含间隙碰撞振动系统，建立了其力学模型，研究了设计参数变化所引起的系统动力学响应从平衡状态到出现分岔及混沌现象的演变过程.通过设计参数包括初始碰撞位置、黏性阻尼因子、刚度和振动台激振频率的变化，得到可以反映系统运动状态的时间历程图、相图、分岔图和Poincaré截面图，全面反映系统周期运动和混沌运动状态的演化过程.根据机械设计参数多元化的特点，提出了两个典型参数变化过程的三维分岔图，为含间隙的碰撞振动机械系统的参数设计提供理论依据.

［1］丁旺才，谢建华.碰撞振动系统分岔与混沌的研究进展［J］.力学进展，2005，35（4）：513－524.

［2］金栋平，胡海岩.碰撞振动与控制［M］.北京：科学出版社，2005.

［3］Peterka F，Tondl A.Phenomena of subharmonic motions of oscillator with soft impact［J］.Chaos，Solutions ＆Fractals，2004，19（5）：1283－1290.

［4］丁旺才，谢建华，李万祥.碰撞振动系统强共振下的两参数动力学分析［J］.计算力学学报，2004，21（6）：658－664.

［5］杨尚普.含非线性弹簧－阻尼碰撞振动系统的动力学研究［D］.兰州：兰州交通大学，2012.

［6］闻邦椿，李以农，徐培民，等.工程非线性振动［M］.北京：科学出版社，2007.

［7］陈予恕.非线性振动［M］.北京：高等教育出版社，2002.

［8］魏艳辉.一类两自由度碰撞振动系统的动力学研究［D］.桂林：广西大学，2007.