考虑舰艇运动的舰炮弹道修正弹速度模型

黄 义，梁德清，秦东兴，徐 明

（1.大连舰艇学院，辽宁 大连116018；2.海军装备部，北京100071）

0 引言

舰炮发射增程弹道修正弹可以克服对岸和对海攻击射程近、精度低的缺点，又可以发挥反应速度快、储弹量多和火力密度大的优点，是目前信息化弹药的研究热点和发展趋势之一［1］。在舰炮弹道修正中，如何由实测的一段弹道参数，实时、准确地推算落点，是极其重要的环节之一［2］，推算落点必须用到弹丸速度。相对地球静止的地面火炮雷达测速模型不适用于舰炮，本文针对舰艇航行中舰炮发射修正弹后，测量外弹道的跟踪雷达随舰艇运动、摇摆和升沉的特点，提出了考虑舰艇运动的两种舰炮弹道修正弹速度模型。

1 舰艇运动时舰炮弹道修正弹坐标模型

设雷达测量的不稳定球坐标转换为稳定直角坐标 为 （xgi，ygi，zgi）（i ＝ 1，2，3，…，n），（xgi，ygi，zgi）（i＝1，2，3，…，n）转换到以发射时刻发射点相对地球所在位置为坐标原点的坐标系O－XYZ中为坐标（xi，yi，zi）（i＝ 1，2，3，…，n）［3］，OX 轴为射击平面与水平面的交线，指向射击方向为正；OY轴在射击平面内，垂直于OX轴，向上为正；OZ轴垂直于平面OXY，按右手法则确定，则

Cwi和Vwi（i＝1，2，3，…，m＋n）分别为舰艇航向和航速，m为从火炮发射修正弹时刻到第一次测量弹道坐标之前记录我舰绝对航速和航向的次数，β为发射修正弹的稳定瞄准方向角，ΔβPG0为火炮平台的方向零位相对雷达平台方向零位的偏差，Δhsci为第i次测量弹道时刻舰艇的升沉减去发射时刻舰艇的升沉之差，V、T为测量弹道坐标的时间间隔和测量舰艇航速、航向的时间间隔。

2 考虑舰艇运动的舰炮弹道修正弹速度模型

2.1 利用弹道坐标计算弹丸速度模型

设（xi，yi，zi）（i＝1，2，3，…，n）的滤波值为（x′i，y′i，z′i）（i＝ 1，2，3，…，n），则弹丸速度在坐标系 O－XYZ 三个坐标轴上的分量（Vxi，Vyi，Vzi）（i＝1，2，3，…，n－1）为：

2.2 利用径向速度计算切向速度模型

径向速度和切向速度的相互关系如图1所示。

图1中，T点为任一被测量的弹道点，T′为T点在水平面O－XY的投影，R点为测量T点时雷达天线中心，Vr为径向速度，V为切向速度，φ为径向速度与切向速度的夹角，θ为弹道倾角，ψ为弹道偏角，α为雷达天线方向所在垂直面与O－XY平面之间的夹角，γ为雷达天线方向与水平面的夹角。

径向速度与切向速度的夹角余弦cosφ为［4］

图1 径向速度和切向速度关系图Fig.1 Relation figure between radial velocity and tangential velocity

设弹丸切向速度与径向速度之间的夹角为φi（i＝1，2，3，…，n），则夹角余弦cosφi（i＝1，2，3，…，n－1）为：

虽然目前边坡区降雨稀少，但随着雨季来临，降雨将是影响边坡稳定性主要因素，一方面降雨入渗使土体饱水，增加了滑体的重量，更重要的另一方面是降雨的入渗，使滑带土饱水软化，抗剪强度降低，力学性状聚变，从而促进了滑坡的发生。

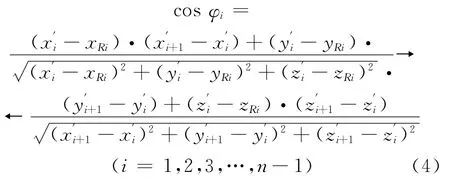
式（4）中，（xRi，yRi，zRi）为跟踪雷达在坐标系O－XYZ中的坐标，计算公式为：

设雷达测量弹丸径向速度为Vri（i＝ 1，2，3，…，n），则利用径向速度计算的弹丸切向速度V′i（i＝1，2，3，…，n－1）为：

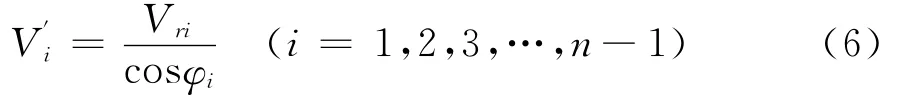
弹丸切向速度V′i（i＝1，2，3，…，n－1）在坐标系O－XYZ 三 个 坐标轴上的 分 速 度 （V′xi，V′yi，V′zi）（i＝1，2，3，…，n－1）为：

3 仿真

假设舰艇航速20kn，航向30°，舰炮发射修正弹的稳定瞄准方向角β＝5°，ΔβPG0＝0°；舰艇横摇范围±12°，周期9s；纵摇范围±5°，周期6s；升沉幅度2m，周期5s。根据舰炮发射修正弹误差构成［5］，假设误差为：

假设舰艇姿态导航仿真精度分3种情形：

情形1：摇摆角测量误差均值为零、均方差为0.7mrad；航速测量误差均值为零、均方差为0.8 kn；航向测量误差均值为零、均方差为0.7mrad。

情形2：摇摆角测量误差均值为0.7mrad、均方差为0.7mrad；航速测量误差均值为0.8kn、均方差为0.8kn；航向测量误差均值为0.7mrad、均方差为0.7mrad。

情形3：摇摆角测量误差均值为－0.7mrad、均方差为0.7mrad；航速测量误差均值为－0.8kn、均方差为0.7mrad。

假设雷达测量弹道仿真精度分3种情形：

情形1：斜距离测量误差均值为零、均方差为10 m；角度测量误差均值为零、均方差为0.8mrad；径向速度测量误差均值为零、均方差为2m／s。

情形2：斜距离测量误差均值为10m、均方差为10 m；角度测量误差均值为0.8mrad、均方差为0.8mrad；径向速度测量误差均值为1m／s、均方差为2m／s；

情形3：斜距离测量误差均值为－10m、均方差为10m；角度测量误差均值为－0.8mrad、均方差为0.8mrad；径向速度测量误差均值为－1m／s、均方差为2m／s。

采用Monte－Carlo法仿真100次，利用弹道坐标求速度（模型一）和利用雷达测量的径向速度求速度（模型二），雷达测量段中间点的合速度误差当舰艇姿态导航精度为情形1、雷达测量精度为情形1时如图2所示；当舰艇姿态导航精度为情形2、雷达测量精度为情形2时如图3所示；当舰艇姿态导航精度为情形3、雷达测量精度为情形3时如图4所示。

从图2、图3和图4可以看出：

1）模型一和模型二的合速度误差绝对值均小于2.0m／s，精度较好，说明两模型是正确的。

2）模型二的合速度误差均方差明显小于模型一。

3）两种模型的合速度误差均值因舰艇姿态导航误差和雷达测量误差的均值不同而不同，当舰艇姿态导航误差和雷达测量误差有系统误差时，模型一的合速度误差均值较模型二小。

4 结论

本文提出并建立了考虑舰艇运动的两种舰炮弹道修正弹速度模型，解决了舰艇运动对修正弹速度计算的影响。模型一利用跟踪雷达测量的相对坐标、测量坐标的时间间隔以及舰艇航速、航向计算修正弹速度；模型二利用跟踪雷达测量的径向速度计算修正弹速度。仿真表明：模型二计算修正弹速度误差的均方差小于模型一；当舰艇姿态导航误差和雷达测量误差有系统误差时，模型一计算修正弹速度误差的均值较模型二小。所以，当舰艇姿态导航误差和雷达测量误差有系统误差时，选用模型一；当舰艇姿态导航误差和雷达测量误差没有系统误差时，选用模型二。

［1］汪德虎，黄义.舰炮对岸信息化制导弹药及作战运用［J］.飞航导弹，2011（2）：37－40.

［2］王中原，史金光，李铁鹏.弹道修正中的控制算法［J］.弹道学报，2011，23（2）：19－21，27.

［3］黄义，汪德虎，王建明.舰载跟踪雷达测量弹道修正弹坐标转换模型［J］.兵工自动化，2012，31（8）：3－5.

［4］王俊.复合增程修正弹弹道参数时序探测技术研究［D］.南京：南京理工大学，2007，43－45.

［5］黄义，汪德虎，余家祥.舰炮一维弹道修正弹射击误差分离和校正研究［J］.指挥控制与仿真，2012，34（3）：44－46.