引信曲折槽机构设计参数灵敏度

程 君，闻 泉，王雨时，义高潮，应益发，涂伟忠

（1.南京理工大学机械工程学院，江苏 南京210094；2.江西星火机械厂，江西 南昌 331729）

0 引言

曲折槽机构具有判别冲击过载幅值及其作用持续时间的特性，一定程度上能够解决勤务处理安全性与发射时解除保险正确性的矛盾，广泛应用于迫击炮引信、火箭引信和无后坐炮引信等较低发射过载的引信中［1－3］。

文献［4］采用无量纲模型，分析了曲折槽机构解除保险灵敏度，增大惯性簧刚度和预压抗力、增加曲折槽段数、减轻惯性筒质量等措施可提高对速度变化量的识别能力。文献［5］应用刚体动力学理论建立了解除保险过程的数学模型，定量分析了惯性簧刚度、惯性簧预压量、惯性筒质量、导向销与曲折槽间的摩擦系数、曲折槽倾角等结构参数对解除保险性能的影响。文献［6］在考虑扭力矩作用基础上，建立了曲折槽保险机构的解除保险过程动力学模型，得出引信跌落到松软地面上时扭力矩对惯性筒位移响应影响明显。但上述数学模型均是建立在理论分析基础上，忽略了曲折槽机构特定结构对机构运动的影响，如惯性筒上曲折槽宽度影响导向销与曲折槽间碰撞、曲折槽过渡圆角影响惯性筒速度变化、曲折槽深度影响导向销簧抗力等。

本文结合火箭弹引信曲折槽保险机构设计实例，针对从理论上无法分析引信曲折槽机构曲折槽宽度、过渡圆角和深度对机构动态特性影响的问题，提出采用ADAMS动力学分析软件对曲折槽机构解除保险过程及结构参数进行仿真分析。

1 曲折槽保险机构作用原理

曲折槽保险机构物理结构示意图如图1所示。勤务处理引信意外跌落时曲折槽保险机构中的惯性筒会沿导向销边转动边向下运动。但由于跌落时惯性力作用时间很短，惯性筒的转动、槽壁与导向销的摩擦和拐角处的碰撞将动能消耗完，故被保险部件不会被惯性筒释放。随后在惯性簧推力作用下，惯性筒又恢复到初始装配状态，保证引信处于安全状态。

发射时，由于弹丸加速运动过程中后坐力作用时间足够长，惯性筒在后坐力作用下一直运动到底，释放被保险件。惯性筒运动到位后，导向销在导向销簧抗力作用下向前伸出挡住惯性筒，防止后坐力消失后惯性筒在惯性簧作用下恢复到位，如图2所示。

图1 曲折槽保险机构物理结构示意图Fig.1 Physical structure diagram of zigzag arming device

图2 曲折槽保险机构运动状态Fig.2 Kinematical state of zigzag arming device

2 ADAMS仿真及试验验证

2.1 模型建立

分析的曲折槽机构主要参数为：惯性筒质量m＝2.67g，惯性簧刚度为K＝65.26N／m，曲折槽倾角为a＝45°，导向销小端直径d＝2mm，曲折槽宽d＝2mm，过渡圆角R＝1mm，曲折槽深度h＝2 mm。利用Solidworks三维绘图软件建立曲折槽保险机构仿真分析模型，将建立的模型保存为Parasolid.X＿T格式，然后利用ADAMS／View模块提供的数据交换接口，将模型文件导入到ADAMS软件中，后修改构件名称和材料信息，添加接触副和运动副，并进行仿真［7］。曲折槽保险机构约束关系见表1所列。

表1 曲折槽保险机构约束关系Tab.1 Constraint relations of zigzag arming device

2.2 模型加载

发射过程中不同时刻火箭推力数据无法表达为一个已知的函数，需将这些数值进行拟合，得到拟合曲线作为火箭推力的变化规律曲线。选用ADAMS中CUBSPL函数插值方式，将后坐过载通过函数CUBSPL（time，0，SPLINE＿1，0）施加在惯性筒上。图3为通过创建函数得到的火箭发动机F－T曲线。

图3 火箭发动机F－T曲线Fig.3 F－T curve of rocket engine

2.3 解除保险正确性仿真

利用ADAMS仿真曲折槽保险机构在发射过程中惯性筒的运动状态及解除保险过程，判断其解除保险正确性。图4为仿真得到的发射过程中曲折槽保险机构运动情况。

由图4可知发射过程中惯性筒在后坐力作用下沿导向销边转动边向下运动，一直运动到底，直至与簧柱发生碰撞。惯性筒运动到位后，导向销前伸挡住惯性筒，保证惯性筒解除被保险件后的作用正确性。

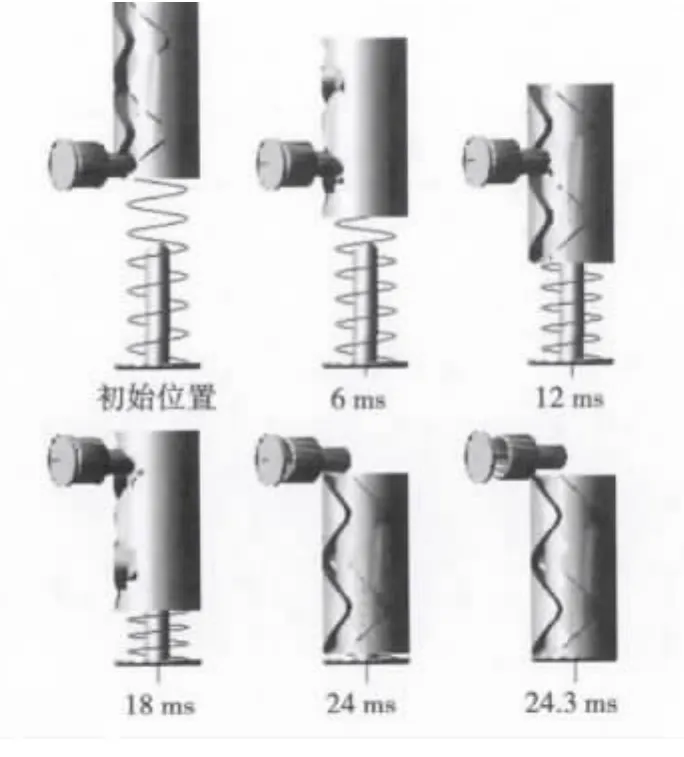
图4 发射时曲折槽保险机构运动过程Fig.4 Movement of zigzag device during launch

图5为发射过程中惯性筒运动速度和位移响应曲线。由图5可看出惯性筒通过每一段曲折槽时运动速度都有发生波动，说明惯性筒在向下运动过程中与导向销发生不同程度的碰撞，从而消耗惯性筒运动能量，使惯性筒下降速度减缓，这一特性符合曲折槽后坐保险机构作用特性。曲折槽保险机构在发射过程中运动到位的时间为24.3ms，而火箭发动机工作时间在100ms左右，因此通过仿真分析可知曲折槽机构能可靠解除保险。

图5 惯性筒运动速度和位移响应曲线Fig.5 Velocity curve and displacement curve of inertia cylinder

2.4 勤务处理安全性仿真

利用ADAMS仿真曲折槽保险机构在勤务处理过程中惯性筒的运动状态，判断曲折槽保险机构是否在勤务处理中解除保险。分别仿真了引信从1.5m落高分别跌向钢板、水泥地和沙土时勤务处理安全性。跌落目标参数［7］见表2所列。引信跌向3种目标时惯性筒轴向位移及惯性筒恢复到位时间如表3所列。其中跌落目标为钢板时，曲折槽保险机构运动过程如图6所示。

由运动过程可知，在勤务处理跌落钢板过程中，惯性筒向下运动0.18ms左右就和导向销发生碰撞，碰撞后惯性筒速度减小，逐渐趋近于零。之后惯性筒在惯性簧的抗力作用下开始向上运动，恢复到保险机构装配状态。在勤务处理跌落到钢板过程中导向销与第一段曲折槽发生碰撞后，惯性筒向下运动就终止，因此惯性筒不会释放被保险件，符合曲折槽保险机构作用特性。从表1可知引信跌向钢板、水泥地和沙土时惯性筒向下运动轴向位移分别为2.6mm、2.9mm、6.2mm，而曲折槽机构解除保险行程为13.5mm，因此引信1.5m跌向钢板、水泥地和沙土时曲折槽机构都不会解除保险，保证勤务处理安全性。

表2 跌落目标材料参数Tab.2 The material parameter of drop target

表3 勤务处理安全性仿真结果Tab.3 The results of simulation during service

图6 勤务处理中曲折槽保险机构运动过程Fig.6 Movement of zigzag device during service

2.5 试验验证

为了验证仿真结果可信性，对引信进行离心试验和跌落试验，其中跌落试验目标分别为钢板、水泥地和砂土，连续跌落两次，结果如表4所列。射击试验结果如表5所列。试验结果表明曲折槽保险机构能够保证勤务处理安全性和发射时解除保险正确性。

表4 跌落试验结果Tab.4 The results of drop test

表5 射击试验结果Tab.5 The results of firing test

3 参数分析

3.1 曲折槽宽度的影响

因受曲折槽保险机构空间尺寸限制，在此按等差数列分别取曲折槽宽度为2.0mm、2.2mm、2.4 mm三种情况进行动力学仿真。曲折槽宽度对惯性筒速度响应和位移响应影响如图7所示。

从图7可知，曲折槽宽度越大，惯性筒运动到位的时间越短，惯性筒运动速度变化的也越快。曲折槽宽度为2.0mm、2.2mm、2.4mm 时惯性筒运动到位时间分别为24.0ms、21.0ms、20.0ms。从惯性筒运动速度响应可以看出，曲折槽宽度越大，导向销与曲折槽之间间隙就越大，惯性筒运动过程中导向销与曲折槽间碰撞就越严重，碰撞过程中惯性筒动能消耗就越多，从而影响惯性筒的运动。但曲折槽宽度越大，导向销与曲折槽间摩擦力越小，导向销对惯性筒运动阻滞就不明显，惯性筒运动到位的时间就越短，不利于曲折槽保险机构勤务处理安全性。因此增大曲折槽宽度有利于曲折槽机构解除保险，反之有利于勤务处理安全性。

3.2 曲折槽过渡圆角的影响

在原有设计曲折槽过渡圆角R为1.0mm基础上，另按等差数列取圆角为0.5mm、1.5mm共三种情况进行动力学仿真。曲折槽过渡圆角对惯性筒速度响应和位移响应影响如图8所示。

从图8可知，曲折槽过渡圆角越大，惯性筒运动到位的时间就越短，惯性筒运动的速度也变化得越快。曲折槽圆角为0.5mm、1.0mm、1.5mm 时惯性筒运动到位时间分别为27.5ms、24.0ms、21.2 ms。曲折槽过渡圆角对惯性筒运动影响明显，增大曲折槽过渡圆角有利于曲折槽机构解除保险，反之有利于勤务处理安全性。

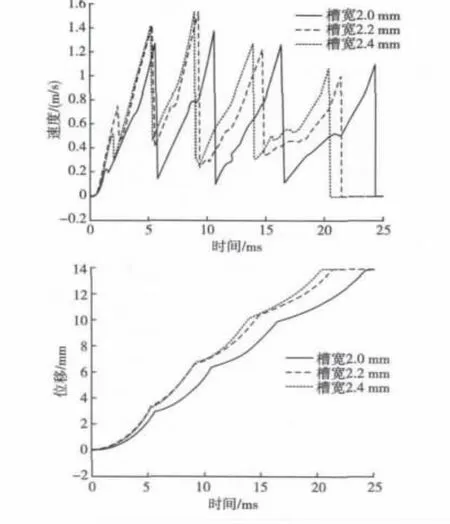
图7 曲折槽宽度对惯性筒速度和位移影响Fig.7 The influence of zigzag width on speed and displacement of inertial cylinder

图8 曲折槽过渡圆角对惯性筒速度和位移影响Fig.8 The influence of zigzag fillet on speed and displacement of inertial cylinder

3.3 曲折槽深度的影响

因受曲折槽保险机构空间尺寸限制，在此按等差数列分别取惯性筒上曲折槽深度为1.8mm、2.0 mm、2.2mm三种情况进行动力学仿真。曲折槽深度对惯性筒速度响应和位移响应影响如图9所示。

图9 曲折槽深度对惯性筒速度和位移影响Fig.9 The influence of zigzag depth on speed and displacement of inertial cylinder

从图9可知，曲折槽深度越大，惯性筒运动到位的时间越短，惯性筒运动的速度也变化越快。曲折槽深度为1.8mm、2.0mm、2.2mm时惯性筒运动到位时间分别为24.5ms、24.0ms、23.5ms。导向销与曲折槽之间存在摩擦力，导向销运动通过导向销簧抗力来提供，曲折槽深度直接影响导向销簧的预压量，从而影响导向销簧抗力大小和两者之间摩擦力的大小。曲折槽深度越大，导向销与惯性筒间摩擦力越小，反之越大。因此增大曲折槽深度有利于曲折槽机构解除保险，反之有利于勤务处理安全性。

4 结论

本文提出了采用ADAMS软件对火箭弹引信曲折槽保险机构解除保险可靠性和勤务处理安全性进行仿真研究，分析了惯性筒上曲折槽宽度、曲折槽过渡圆角和曲折槽深度等设计参数对机构动态的影响。结果表明：该引信曲折槽保险机构在80 g发射过载下能可靠解除被保险部件，在1.5m高度跌落钢板、水泥地和砂土目标能保证被保险部件安全性，与试验结果相符；在一定范围内增大惯性筒上曲折槽宽度、曲折槽拐角处圆角及曲折槽深度均有利于曲折槽保险机构解除保险，反之则有利于勤务处理安全性。该方法将为曲折槽保险机构的工程设计提供参考。

［1］《引信设计手册》编写组.引信设计手册［S］.北京：国防工业出版社，1978.

［2］王晖，陈荷娟.复合式惯性制动保险机构及性能分析［J］.探测与控制学报，2007，29（1）：32－35.

［3］宋丽萍.复合受力蛇形槽保险机构性能分析［J］.华北工学院学报，1999，20（1）：10－13.

［4］谭惠民，齐杏林.曲折槽机构的灵敏度分析［J］.兵工学报，1994，11（4）：66－69.

［5］檀永杰.引信曲折槽后坐保险机构理论研究［D］.南京：南京理工大学，2008.

［6］周彬，安振涛，秦翔宇.扭力矩对曲折槽保险机构动力学响应影响分析［J］.军械工程学院，2009，21（5）：33－37.

［7］郭卫东.虚拟样机技术与ADAMS应用实例教程［M］.北京：北京航空航天大学出版社，2008.