Q235钢基体LZAS微晶玻璃／Y－TZP梯度涂层接触应力的数值模拟

龚 伟，周黎明，王恩泽，白朝中

（1中国工程物理研究院 激光聚变研究中心，四川 绵阳621900；2西南科技大学 制造科学与工程学院，四川 绵阳621010；3西南科技大学 材料科学与工程学院，四川 绵阳621010）

金属表面微晶玻璃涂层在电子工业、航空航天、生物医学等领域具有重要的应用价值。将微晶玻璃介质浆料印刷于不锈钢基板表面，经过干燥、烧成后形成的介质膜层与不锈钢基板共同组成复合基板，可替代传统的陶瓷基板［1］。在钛合金表面涂覆合适的微晶玻璃涂层可有效提高钛合金的高温抗氧化性能［2］。Sen等［3］研究表明，RO－R′2O－Al2O3－SiO2（R＝Ca，Mg；R′＝Na，K，Li）系微晶玻璃涂层可提高零件在干滑动摩擦条件下的耐磨性。金属表面 Li2O－B2O3－Na2OA12O3－SiO2系微晶玻璃的耐磨性和力学性能明显高于普通搪瓷［4］。微晶玻璃涂层在物料输送管道的内衬，选矿厂的料仓、溜槽、水槽、浮选机机体、漏斗和各种排放口等工况场合具有广阔的应用前景。

功能梯度材料（Functionally Graded Materials，FGM）是一种组分、结构和性能均呈连续变化的新型复合材料［5］。研究表明，将FGM用于表面涂层可以显著增强零部件表面抵抗接触破坏和失效的能力［6］。

Li2O－ZnO－Al2O3－SiO2（LZAS）系微晶玻璃软化温度低，并且随制备条件的不同，其热膨胀系数可在一定范围内变化（36.1×10－7～200×10－7℃－1，20～500℃），可用于封接多种金属和合金［7］。

为此，笔者在Q235钢基体上通过涂搪法制备了LZAS微晶玻璃／Y－TZP梯度涂层［8］，该梯度涂层通过热膨胀系数的逐层递变在表层形成残余压应力，提高涂层韧性。

接触应力状态是涂层材料表层破坏、整体分层剥落的重要影响因素。近年来，有限元法成为求解与分析材料接触应力的主要途径。Zhang等［9］利用有限元法对比了单层涂层、功能梯度和三明治结构涂层的接触应力。刘铁军等［10］求解了在不同的剪切模量条件下功能梯度涂层半空间的无摩擦轴对称接触问题，计算了接触应力与接触区半径，最大压入深度之间的关系。相对于单层涂层而言，对梯度涂层接触问题的研究较少。已有的研究主要集中于弹性模量、接触半径等影响因素。梯度层厚度、梯度层层数、物理性能参数渐变方式是制备梯度涂层必须涉及的参数，而有关这些参数对涂层接触应力影响的报道较少。本工作在基于Hertz接触理论的基础上，采用数值模拟方法，分析了Q235钢基体LZAS微晶玻璃／Y－TZP梯度涂层在球形压头法向静载作用下的受力情况，探讨了梯度层厚度、梯度层层数、3Y－TZP体积组分差（假设物性参数沿涂层厚度方向按线性渐变）对涂层接触应力的影响规律，获得最优参数。

1 有限元模型

1.1 Hertz接触基本理论

经典的Hertz接触理论主要基于下列假设［11］：（1）表面都是连续的且非协调；（2）小应变；（3）每个物体都可被看作为一个弹性半空间；（4）表面充分光滑。

当球体与弹性半空间体接触时，由Hertz接触理论可推得其接触表面的压力呈椭圆形分布：

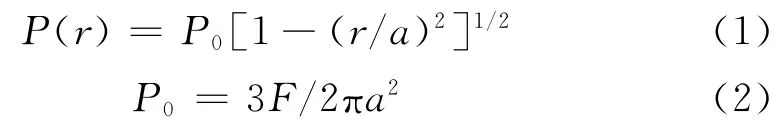
式中：P0为接触区中心的最大压力；a为接触区半径；F为作用于球体的外力。

在上述Hertz压力作用下，根据Johnson的接触理论，可得在接触表面下方沿中心轴z的应力分量：

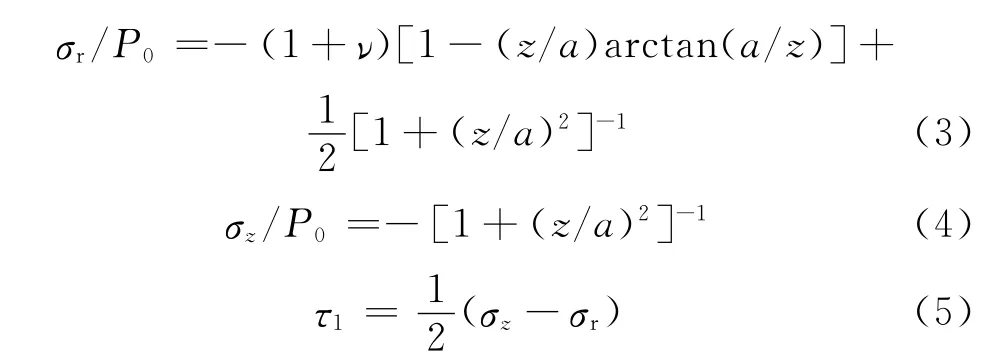
式中：σr，σz和τ1分别为径向应力，轴向应力和剪切应力；z为从接触表面沿z轴到基体方向某点的垂直距离；ν为泊松比。

由接触力学理论可知，接触应力主要与作用力的大小、压头的尺寸及其材料的弹性模量、泊松比等有关。由式（2）～（5）可绘制出接触半平面下的理论应力分布曲线，如图1所示。

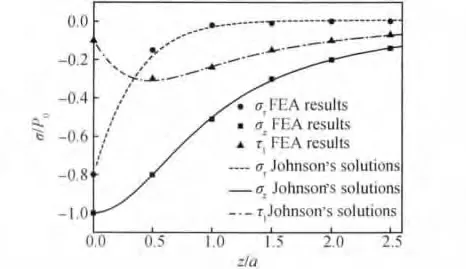
图1 Hertz理论解与有限元数值解的比较Fig.1 Comparison of the finite element results with Hertz theoretical solutions

1.2 有限元模型的建立

图2（a）为Q235钢基体LZAS微晶玻璃／Y－TZP梯度涂层的接触示意图。假定涂层与基体结合良好，可看作为一个整体。将半径R＝2.5mm的球形压头压在厚度为t的涂层上，压头为解析刚体，A点为球心。为了便于求解后取值，将坐标系（O－rz）原点设置于涂层与基体界面几何中心（O点）处，z轴为对称中心轴。

为了节省计算时间，采用二维轴对称模型进行模拟计算，利用ANSYS10.0软件建立接触应力计算的有限元模型，如图2（b）所示。由于在软件中建立的模型位于XY平面内，故原坐标系O－rz可改为坐标系O－xy，即y轴为中心轴，x轴方向为径向。根据对称性边界条件，y轴和点A 在x方向上的位移为零，基体底边y向位移为零。此外，为了保证涂层接触应力的计算精度，将整个涂层区域进行网格细分。涂层有限元网格的水平和垂直方向的尺寸分别为2t／15和t／30。压头为解析刚体，故不必对其进行网格划分。为了便于有限元计算，本工作假设材料各向同性，且性能参数不受温度变化的影响。

图2 梯度涂层的有限元分析模型（a）接触示意图；（b）有限元模型Fig.2 Finite element analysis model of the gradient coatings（a）contact condition chosen for the analysis；（b）finite element model

1.3 材料性能

在利用有限元软件进行计算时，仅需考虑接触物体材料的弹性模量和泊松比。Q235钢、微晶玻璃和3Y－TZP陶瓷的相关物理性能参数如表1所示。

表1 Q235钢、LZAS微晶玻璃及3Y－TZP的物理性能参数Table1 Material properties of Q235steel，LZAS glass－ceramic and 3Y－TZP

Wakashima提出梯度层的组元在涂层厚度方向呈幂函数分布［13］，有利于热应力的缓和。本工作结合实验室已有的研究，确定成分分布指数为1，即3YTZP陶瓷体积分数沿涂层厚度方向由里层至表层线性增加，使得热膨胀系数逐层递减，在涂层表面形成残余压应力，提高涂层韧性［8］。本工作假设涂层每层厚度相等，涂层完全致密，并且不考虑3Y－TZP相变。梯度涂层内每层材料的物性参数则可根据Voight混合法则［14］确定，即：

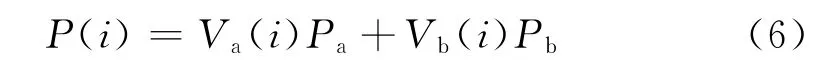
式中：P（i）为梯度涂层中第i层材料的物性参数；Pa和Pb分别为微晶玻璃和3Y－TZP的性能参数；Va和Vb分别为微晶玻璃和3Y－TZP的体积分数。

由式（6）可知，当梯度涂层中3Y－TZP的体积分数沿涂层厚度方向由里至表按一定值递变时，涂层每层材料的物性参数将随之呈线性函数形式变化。

1.4 有限元模型的评估

用一个球形压头作用在无涂层的Q235基体上以评估所建的有限元模型。给压头法向施加1000N的力载荷，将ANSYS计算得到的应力数值解与Johnson接触理论解进行对比，结果如图1所示。由图1可见，有限元模型的数值解与理论解基本一致，表明所建的有限元模型具有较高的可信度。

2 有限元分析结果

2.1 涂层的接触应力分布

改变梯度层厚度、梯度层层数及3Y－TZP体积组分差，涂层接触应力的分布情况基本一致，如图3所示。从图3（a）可以看出，涂层径向的最大接触应力位于表面的接触中心处，为压应力。在接触区域边缘，径向应力沿着表面水平方向由压应力迅速转变为拉应力。这种压、拉应力的突变正是导致脆性涂层失效的主要原因［15］。由于拉应力的值较最大压应力的小很多，因此本工作以最大径向压应力的变化替代压－拉应力的突变。由图3（b）可知，涂层体系的最大剪切应力位于表层下方且靠近坐标原点处。在涂层与基体界面处，剪切应力沿径向先增大后减小。出于对整个涂层性能的考虑，本工作主要分析涂层／基体界面处的剪切应力。图3（c）为涂层Mises应力的分布情况，可以看出，涂层最大的Mises应力位于接触中心处，且沿着涂层厚度方向逐渐减小。由于最大的Mises应力对涂层内部微裂纹的产生起着重要作用［16］，因此本工作也主要分析涂层结构变化对最大Mises应力的影响。

图3 梯度涂层接触应力的分布云图（a）径向应力；（b）剪切应力；（c）Mises应力Fig.3 Stress distribution of the gradient coatings（a）radial stress；（b）shear stress；（c）Mises stress

2.2 涂层层数的影响

当涂层厚度为1mm、梯度层3Y－TZP体积组分差为10%时，涂层表面最大径向应力和整体最大Mises应力与涂层层数的变化关系如图4（a）所示。可以看出，随着梯度层层数的增加，涂层表面最大径向应力和整体最大Mises应力均增大。这主要是由于涂层表层材料中3Y－TZP的含量会随着层数的增加而增多，从而使涂层表层的弹性模量增大，导致接触应力产生了类似线性的递增。

图4（b）为不同层数下涂层／基体界面处剪切应力分布情况。可以看出，剪应力沿着界面方向从坐标原点处开始先增大后减小，且最大值均出现在x／a＝2处。此外，随着涂层层数的增加，就整个涂层而言弹性模量增大，界面剪应力总体上因此表现为略为增大，这与文献［17］的研究结果一致。另外，随着层数增加，在取得剪应力最大值后界面剪应力下降趋势有所减缓，说明增加层数对界面剪应力分布不均匀性有一定缓和作用。综上考虑，选择3～5层为宜。

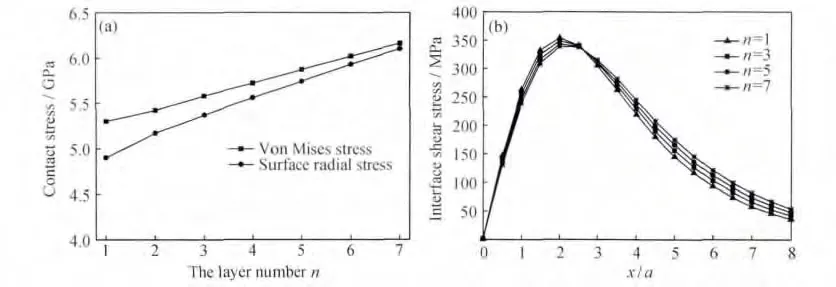
图4 涂层层数与接触应力的关系（a）层数与Mises应力和径向应力；（b）层数与界面剪切应力Fig.4 Relationship between layer numbers and contact stress（a）layer numbers versus Mises stress and radial stress；（b）layer numbers versus interface shear stress

2.3 涂层厚度的影响

当涂层层数n＝5、梯度层3Y－TZP体积组分差为10%时，涂层表面最大径向应力和涂层整体最大Mises应力与涂层层厚的关系如图5（a）所示。可以看出，涂层表面最大径向应力和整体最大Mises应力均随着涂层厚度的增加而减小。由此可见，增加涂层厚度可以显著改善涂层在载荷作用下的受力情况，提高涂层的承受能力和寿命，故在设计涂层结构时应尽力避免涂层过薄。

图5（b）为不同涂层厚度下涂层／基体界面处剪应力分布情况。可以看出，剪应力沿着界面方向从坐标原点处开始先增大后减小，且剪应力峰值随着层厚的增加而减小，应力峰位置逐渐偏离中心轴位置。此外，随着涂层厚度的增加，剪应力突变量减小，说明应力梯度减小，应力分布均匀性提高。由此可见，增加涂层的厚度可以减小涂层／基体界面处的剪应力，避免涂层与基体出现脱粘现象而导致涂层剥落。但是，随着层厚的增大，远离中心轴的区域仍存在较大的界面剪应力，反而会对涂层与基体的结合强度产生不利的影响，而且增加层厚还将增加涂层的制备成本。综上考虑，涂层厚度选择1.0～1.5mm为宜。

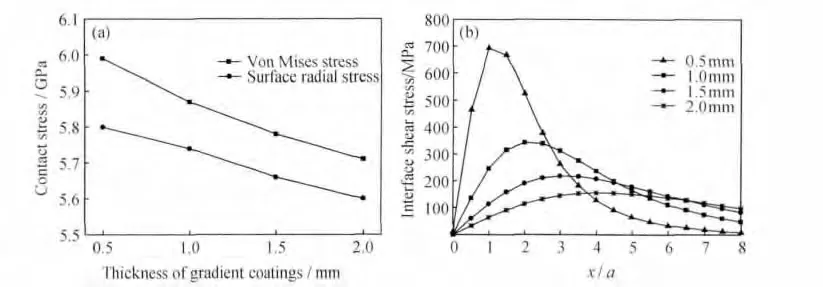
图5 涂层厚度与接触应力的关系 （a）层厚与Mises应力和径向应力；（b）层厚与界面剪切应力Fig.5 Relationship between coating thickness and contact stress（a）coating thickness versus Mises stress and radial stress；（b）coating thickness versus interface shear stress

2.4 3Y－TZP体积组分差的影响

当涂层层数n＝5、厚度为1.0mm时，涂层表面最大径向应力和涂层整体最大Mises应力与梯度层3YTZP体积组分差的关系如图6（a）所示。可以看出，随着梯度层组分差的增加，涂层表面最大径向应力和整体最大Mises应力都明显增大。这主要是由于在相同厚度和层数的条件下，梯度组分差越大，涂层表层中3Y－TZP的含量就越多，从而使涂层表层的弹性模量增大，导致表层接触应力逐渐提高。

图6 3Y－TZP体积组分差与涂层接触应力的关系（a）3Y－TZP体积组分差与Mises应力和径向应力；（b）3Y－TZP体积组分差与界面剪切应力Fig.6 Relationship between the volume difference of 3Y－TZP in various gradient layers and contact stress（a）volume difference of 3Y－TZP versus Mises stress and radial stress；（b）volume difference of 3Y－TZP versus interface shear stress

图6（b）为不同的梯度层3Y－TZP体积组分差下涂层／基体界面处剪应力分布变化情况。可以看出，剪应力沿着界面方向从表面接触中心处开始先增大后减小，且最大值均出现在x／a＝2处。此外，随着组分差增加，由于涂层弹性模量增大，界面剪应力总体上表现为略微增大。另外，随着组分差加大，在取得剪应力最大值后界面剪应力下降趋势有所减缓，说明增大组分差对剪应力分布不均匀性有一定缓和作用。但是随着组分差的增加，表面最大径向应力和整体最大Mises应力都会增大，反而会增加涂层表面破损的风险。因此综合分析，梯度层3Y－TZP体积组分差选择5%～8%较为合适。

3 结论

（1）通过比较有限元数值解和Hertz理论解，验证了ANSYS有限元模型的可靠度。

（2）涂层的径向接触应力和Mises应力的最大值均位于接触中心处，最大剪切应力则位于涂层表层下方且靠近接触中心处，且在涂层／基体界面处，剪切应力沿径向先增大后减小。

（3）随着涂层层数的增加，涂层表面最大径向应力和整体最大Mises应力均增大。涂层层数增加，涂层／基体界面剪应力略为增大，但界面剪应力分布的不均匀性有一定缓和。

（4）随着涂层厚度增大，涂层表面最大径向应力和整体最大Mises应力减小。增大涂层厚度可以减小涂层／基体界面处的剪应力，提高剪应力均匀性。但层厚越大，界面剪应力的分布范围也会扩大。

（5）随着涂层3Y－TZP体积组分差增大，涂层表面最大径向应力和Mises应力均增大。组分差增大，涂层／基体界面剪应力略为增大，但界面剪应力分布的不均匀性有一定缓和。

［1］芦玉峰，楼淼，邓利蓉，等.0Cr18Ni9不锈钢基板BAS系微晶玻璃介质层的研制［J］.功能材料，2010，41（12）：2216－2219.LU Y F，LOU M，DENG L R，et al.Research of dielectric coatings for 0Cr18Ni9stainless steel substrate prepared by BaOAl2O3－SiO2glass－ceramics［J］.Journal of Functional Materials，2010，41（12）：2216－2219.

［2］田鹏，刘新年，李争显，等.钛合金表面抗氧化玻璃－陶瓷涂层研究进展［J］.中国陶瓷，2010，46（4）：2－7.TIAN P，LIU X N，LI Z X，et al.Research progress of oxidationresistant glass－ceramic coatings on titanium alloys［J］.China Ceramics，2010，46（4）：2－7.

［3］SEN R，DUTTA S，DAS S K.Evaluation of a glass－ceramic coating for machine tool slides［J］.Wear，1989，130（1）：249－260.

［4］江利，李植.金属表面玻璃－陶瓷复合涂层的磨粒磨损特性的研究［J］.摩擦磨损，1989，（2）：21－26.JIANG L，LI Z.Study of wear resistance performance of glassceramic coatings on metal substrate［J］.Friction and Wear，1989，（2）：21－26.

［5］边洁，王威强，管从胜，等.梯度功能材料研究的一些进展［J］.金属热处理，2003，28（9）：13－19.BIAN J，WANG W Q，GUAN C S，et al.Review of some research progress of functionally graded materials［J］.Heat Treatment of Metals，2003，28（9）：13－19.

［6］SURESH S.Graded materials for resistance to contact deformation and damage［J］.Science，2001，292（5526）：2447－2451.

［7］LU A X，KE Z B，XIAO Z H，et al.Effect of heat－treatment condition on crystallization behavior and thermal expansion coefficient of Li2O－ZnO－Al2O3－SiO2－P2O5glass－ceramics［J］.Journal of Non－Crystalline Solid，2007，35（3）：2692－2697.

［8］ZHOU L M，GONG W，WANG E Z.Analysis on the residual stress in functionally gradient Fe360／glass－ceramic coatings［A］.The 2nd International Conference on Key Engineering Materials and Computer Science［C］.Zurich：Trans Tech Publications Ltd，2013.215－220.

［9］ZHANG X C，XU B S，WANG H D，et al.Hertzian contact response of single－layer，functionally graded and sandwich coatings［J］.Materials ＆ Design，2007，28（1）：47－54.

［10］刘铁军，汪越胜.功能梯度材料涂层半空间的轴对称光滑接触问题［J］.固体力学学报，2007，28（1）：49－54.LIU T J，WANG Y S.Axisymmetrical smooth contact problem of functionally gradded coated half－space［J］.Acta Mechanica Solida Sinica，2007，28（1）：49－54.

［11］JOHNSON K L.接触力学［M］.徐秉业，译.北京：高等教育出版社，1992.JOHNSON K L.Contact Mechanics［M］.Translated by XU B Y.Beijing：Higher Education Press，1992.

［12］孙静.氧化锆基复合陶瓷纺织剪刀材料的研制及其应用基础研究［D］.济南：山东大学，2005.SUN J.Study on fabrication and application fundamentals of zir－conia matrix composite ceramic materials for spinning and weaving scissors［D］.Jinan：Shandong University，2005.

［13］程西云，何俊，王如团.梯度涂层结构设计制备及应用研究现状［J］.润滑与密封，2010，35（11）：111－114.CHENG X Y，HE J，WANG R T.The structure design of function graded material coating and its application development［J］.Lubrication Engineering，2010，35（11）：111－114.

［14］刘红兵，陶杰，张平则，等.功能梯度Al2O3涂层残余应力分析［J］.机械工程学报，2008，44（8）：26－32.LIU H B，TAO J，ZHANG P Z，et al.Simulation of residual stresses in functionally gradient Al2O3coatings［J］.Chinese Journal of Mechanical Engineering，2008，44（8）：26－32.

［15］楼小玲，柴国钟，鲍雨梅，等.基于Hertz接触理论的涂层界面应力分析［J］.浙江工业大学学报，2006，34（5）：563－566.LOU X L，CHAI G Z，BAO Y M，et al.Analysis of interfacial stress on coatings based upon Hertz contact theory［J］.Journal of Zhejiang University of Technology，2006，34（5）：563－566.

［16］DIAO D F，SAWAKI Y，SUZUKI H.Effect of interlayer on maximum contact stresses of hard coating under sliding contact［J］.Surface and Coatings Technology，1996，86－87（2）：480－485.

［17］陈东，谢华，陈小文.TiN涂层／基体接触应力的有限元分析［J］.材料研究与应用，2010，4（3）：192－198.CHEN D，XIE H，CHEN X W.Finite element analysis of the contact stress of TiN coating／substrate［J］.Materials Research and Application，2010，4（3）：192－198.