超材料结构单元轮廓法对吸波材料衰减吸收频带的拓宽与优化
2014-11-30黄大庆康飞宇周卓辉丁鹤雁
黄大庆,康飞宇,周卓辉,刘 翔,丁鹤雁
(1清华大学 材料学院,北京100084;2北京航空材料研究院,北京100095)
超材料由于其具有负折射率和负磁导率的奇异特性而引起了人们广泛的关注[1],随后不同的实现负折射率的设计方案被研究者们提出来[2-4],从早期的超级透 镜[5]到电磁隐身 斗篷[6]再到波导器件[7],研究者们在不断地把超材料应用到众多领域。然而,超材料的最大特点是其几何尺寸的可设计性实现期望的介电常数和磁导率,这就为超材料在微波吸收材料中的应用奠定了基础。Landy等[8]将超材料引入了吸波材料中实现微波段的窄带的完美吸收,但对于吸波材料而言,窄带完美吸收不能满足实际应用需求,实现宽频衰减吸收是超材料吸波体应用的基本要求。由于超材料单元的几何尺寸直接决定了其谐振频率点的位置,所以不少研究者通过不同尺寸超材料结构的组合,来实现多带宽甚至宽频的吸收[9,10]。然而,这种单元间的组合并不是无限制的,因为超材料结构的设计必须符合等效媒质理论,这就要求周期性单元的尺寸必须小于波长的1/5,过多单元的组合会破坏整体结构的周期性,从而导致谐振吸收的消失,这就极大地限制了超材料单元的组合对频带扩展的作用。因此,需要进一步研究拓展超材料吸波体带宽的技术途径。
本工作首先设计了一种超材料吸波体,模拟仿真计算了其谐振频率点,并分析了其表面电流分布情况;然后对这个模型进行了取轮廓的处理,在发现这种处理后的轮廓对其谐振吸收基本上没有影响的基础上,在这个轮廓模型中加入了其他的谐振单元,研究了通过单元间的组合实现拓宽微波衰减吸收频带的技术途径,最后通过激光刻蚀的方法,研制了实际材料样品,在实验上对所设计的模型进行了验证。
1 模型设计
实验设计的模型如图1(a)所示,经过大量的仿真实验,得到的模型尺寸如下:外正方形边长a=8mm、开口g=2.8mm、所有金属条的宽度w=1.2mm、背板为金属板,所有的金属都为铜,其厚度为0.017mm,导电率为5.88×107S/m。谐振结构和金属背板分别处于边长c=12mm、厚度为2mm的FR4基板(E=4)正反两面。
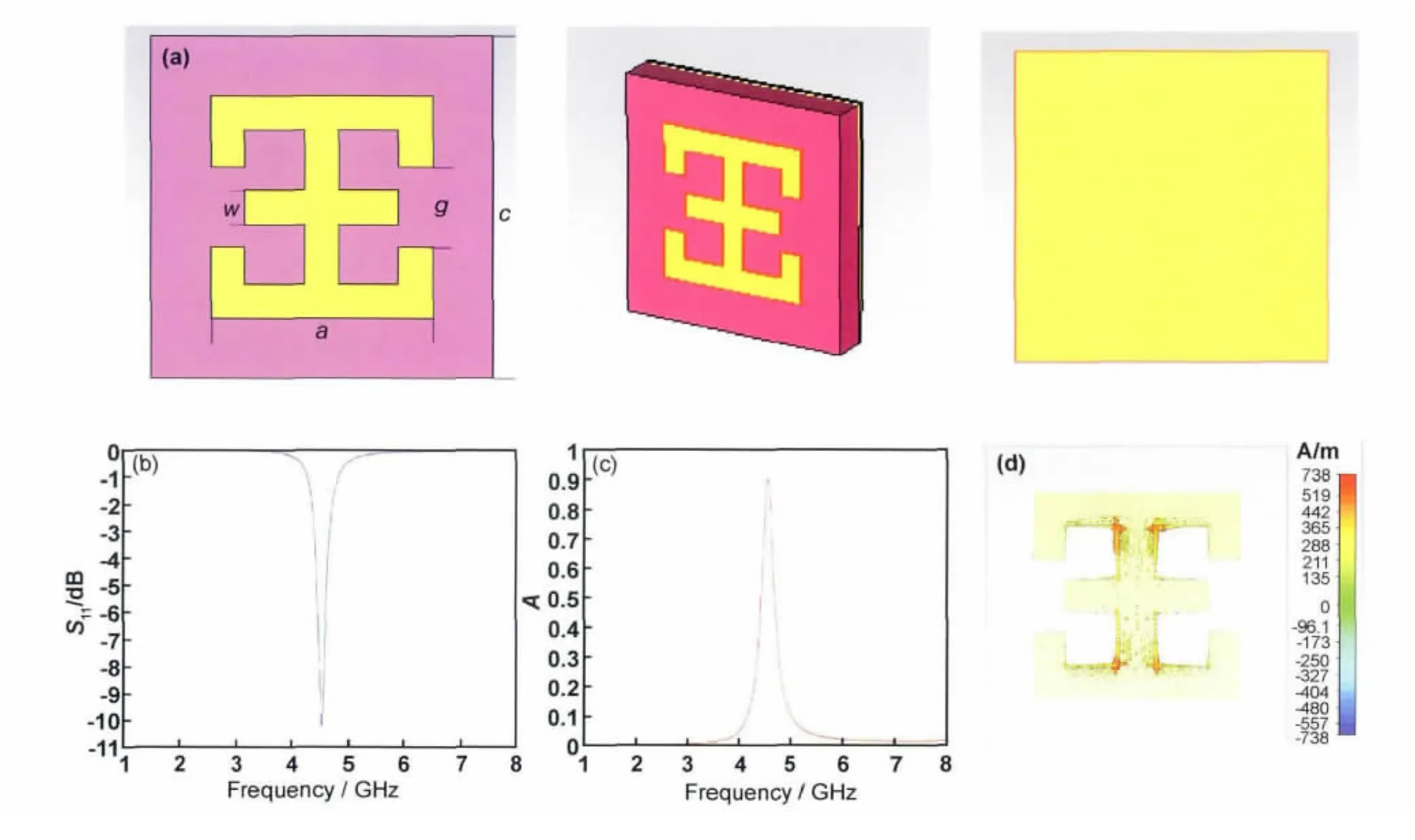
图1 模型的不同视角及其计算结果(a)模型的三种视角;(b)模型的S11参数;(c)吸收曲线;(d)表面电流分布Fig.1 Different perspective of the model and the results of calculation(a)three kinds of perspective of the model;(b)S11parameter of the model;(c)absorption curve;(d)surface current distribution
2 仿真结果和数据分析
数字仿真是采用基于有限差分法来计算金属-电介质结构的透射参数与反射参数的CST Microwave Studio软件进行的,在1~8GHz频段,对图1(a)中的一个单元的超材料结构进行了仿真研究。在垂直入射电磁波的激励下仿真计算了一个单元吸波体的散射参数,如图1(b)所示。从图中可以看出,在4.5GHz左右出现了一个吸收峰,由于背板为金属,透过率S212可以认为是0,所以这个模型的吸收率[11]A=1-S112-S212,其在谐振频点处达到了0.90以上(图1(c));进一步分析其谐振点的表面电流分布发现(图1(d)),大部分电流集中分布在金属结构的边缘,这就为基本不改变谐振点位置的前提下最大限度简化超材料结构提供了可能。
因此,对这个模型进行了轮廓化处理,由于一般PCB板加工的精度在3~6mil(0.075~0.15mm),所以为了满足工业领域加工精度要求,实验中取其轮廓线的宽度w=0.2mm。模型如图2(a)所示,其余尺寸不变,在垂直入射电磁波的激励下仿真计算了一个单元吸波体的S参数,结果如图2(b)。

图2 轮廓化处理后的模型及其计算结果(a)轮廓化处理后模型的三种视图;(b)S11参数;(c)表面电流分布Fig.2 Contour of the model and the results of calculation(a)three kinds of perspective of the model contour;(b)S11parameter;(c)surface current distributions
从图1(b)和图2(b)的S11参数对比可以看出,轮廓模型使原始模型的谐振频点向低频有所移动,但变化不是很大,其在吸收深度上有所加深。通过观察分析这两个模型谐振点的电流分布可以看出(图2(c)),轮廓模型在结构外环上产生了一定强度的电流分布,而在原始模型上最外边缘几乎没有电流分布,因此认为对原始模型取轮廓后,由于外轮廓与内轮廓之间的距离,产生了一个寄生电容,相当于在原来的电容上并联了一个电容,根据LC谐振电路的计算公式f0=可知,增加的这部分电容C1使得谐振频点向低频移动了,与此同时由这个电容所组成的环路还起到了增加电磁场能量消耗的作用,使得吸收峰变得更深;更深入观察发现,这种结构模型在谐振点所激发的电流模式都是从上而下的,这为以后分析多带宽电流分布是由哪个结构决定的提供了重要的依据。
3 双吸收带的实现
在模型轮廓处理研究工作的基础之上,对通过不同结构参数模型的组合来实现双吸收峰的结构进行了研究。通过大量的仿真实验得到了一种实现双吸收带宽的组合结构,结果如图3所示。
中间“王”字型的结构是原始结构模型的简化版本,其结构参数为:高度h0=7mm,宽度b=6mm,b1=3.6mm,线宽w=0.2mm。由仿真结果的S11参数可以看出(图3(b)),这个模型分别在3.4GHz和5.2GHz处出现了吸收峰,并且其低频吸收峰比高频吸收峰浅(图3(c))。进一步观察其谐振频点的表面电流分布发现(图3(d)),在低频谐振时,外轮廓上的电流分布和图2(c)的表面电流分布相同,而“王”字形结构和图2(c)的表面电流分布相反,这说明低频谐振主要是由外轮廓谐振产生的。而“王”字形结构的反向电流分布起到了抑制外轮廓感应电流产生的磁场消耗入射电磁波磁场的能力,使得吸收峰变浅。为了进一步说明这个问题,可以对整个结构的谐振模式进行分析[11],首先,超材料谐振是由两种谐振模式组成的,第一种是超材料结构金属单元和背板之间产生的磁耦合,另外一种是单元和单元之间产生的电耦合,而磁耦合是引起表面电流分布的主要原因。在这个模型中,其入射的磁场方向垂直于谐振环和金属背板,根据楞次定理,由磁通量的改变而产生的感应电流方向,总是在阻碍磁通量的改变,所以,金属结构上表面电流的方向一定与入射磁场的变化趋势有关,而不同结构的表面出现了不同方向的感应电流必然是由于不同的磁通量变化趋势引起的,“王”字型金属上感应电流产生的磁场是阻碍外轮廓感应电流产生的磁场的,那么这样就减少了谐振时外轮廓对入射电磁波磁场的消耗能力,吸收峰变浅。同时,“王”字形结构的电谐振产生了一个寄生电容,相当于在原来的电容上并联一个电容,吸收峰向低频移动,使得低频吸收峰的位置比单独由外轮廓产生的吸收峰的位置低。
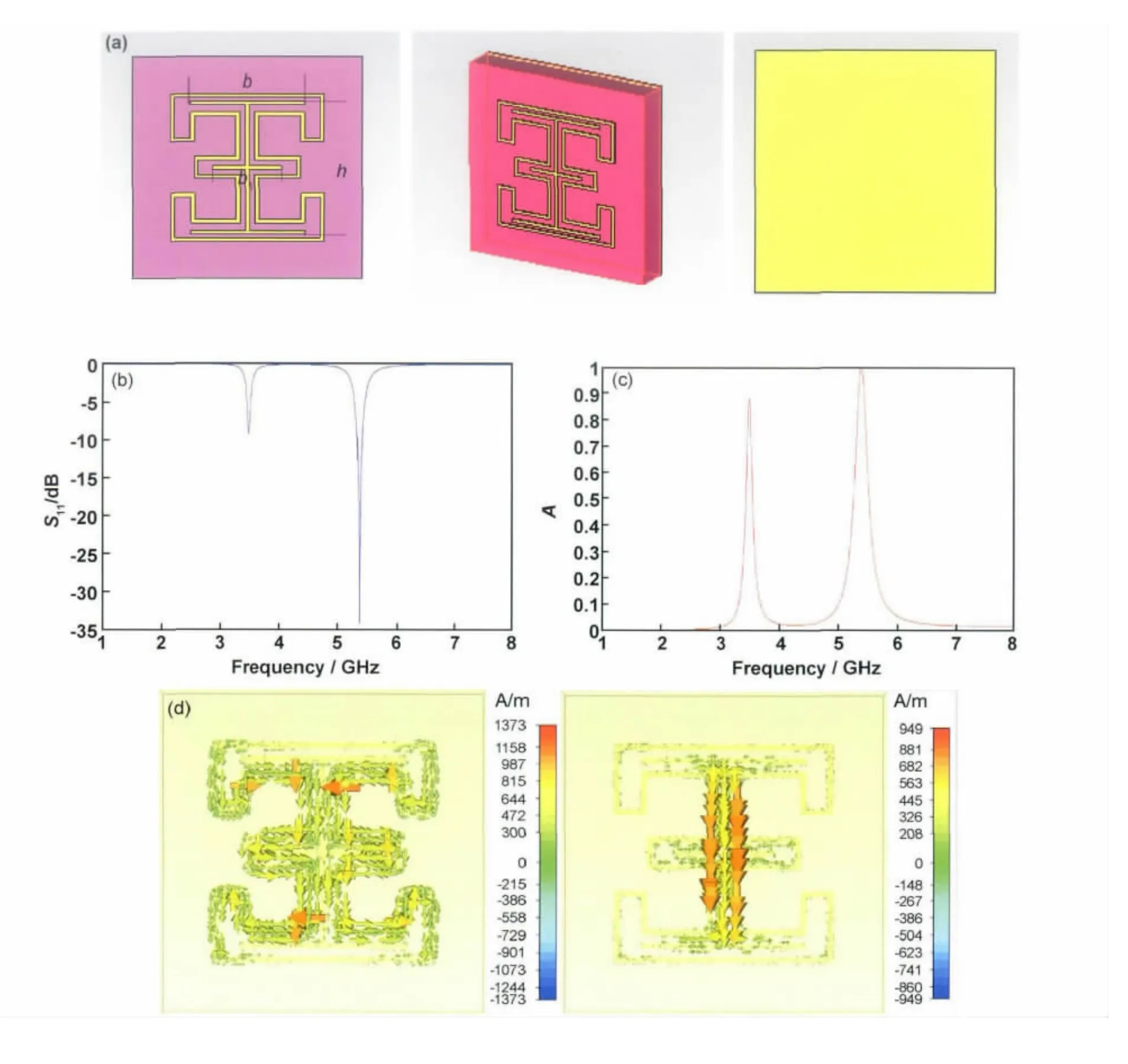
图3 超材料轮廓组合结构模型(a)三种视角图;(b)S11参数;(c)吸收曲线;(d)左图为低频谐振点的表面电流分布图,右图为高频谐振点的表面电流分布图Fig.3 The combination of the metamaterial contour model(a)three kinds of perspective of the combination model;(b)S11parameter;(c)absorption curve;(d)the left picture shows surface current distribution at low resonant point and the right picture shows surface current distribution at high resonant point
在高频谐振时,只在“王”字型结构上产生了表面电流,并且其表面电流的分布与图2(c)的一样,所以高频谐振是由“王”字型结构谐振产生的,同时,由于外轮廓没有产生反向感应电流的阻碍,从而使得电流强度非常小的“王”字型结构产生了比低频谐振时更深的吸收峰。为了进一步清楚地说明这个问题,实验中对“王”字型结构单独进行了仿真,仿真结果如图4所示,发现没有外轮廓的情况下,谐振频点依然是处于5.6GHz左右,并且其表面电流分布和组合结构中高频时其表面电流分布一样(图4(c)),所以外轮廓的作用也仅仅只是增加了寄生电容而拉低了谐振频率点。
4 实验结果

图4 “王”字形结构及其吸收特征(a)三种视角图;(b)S11参数;(c)表面电流分布Fig.4 “王”shape and its absorption characteristic(a)three kinds of perspective of the model;(b)S11parameter;(c)surface current distribution


图5 不同结构的仿真与实物对比(a)原型结构;(b)镂空结构;(c)组合结构;(d)“王”字结构Fig.5 Comparing different simulation and samples(a)the prototype structure;(b)the hollow structure;(c)the composite structure;(d)the“王”structure
为了进一步说明实验结果的正确性,实验中通过激光刻蚀技术制作了所有的计算模型(图5),并用弓形法反射率测量方法对其S11参数进行了测量。从图5可以很明显地看出,实验结果与仿真结果具有很好的一致性,谐振频点的微小移动是由超材料制作上尺寸的微小误差所造成的,而吸收深度的变浅是由测量误差所引起的,在实际测量中,由于软件的拟合等因素,不可能出现在仿真结果中出现的那么尖的吸收峰。排除这些因素的影响,可以说实验结果完全验证了超材料轮廓法拓宽吸波材料衰减吸收频带的技术思路。
5 结论
(1)设计了一种超材料吸波体,通过模拟仿真计算确定了其谐振中心频率的位置,并分析了其表面电流的分布情况,发现了谐振中心处频点的表面电流位置主要分布在超材料结构的边缘。
(2)在超材料结构模型进行轮廓化处理,仿真结果显示,处理后的轮廓对其谐振吸收基本上没有影响。
(3)在轮廓模型中加入了新的谐振单元,通过单元间的组合实现了双频带的微波衰减吸收,通过激光刻蚀技术对设计的模型进行了实验验证,实验结果表明与仿真结果具有很好的一致性,验证了超材料轮廓法拓宽吸波材料的技术思路,为宽频带超材料吸波体的研究提供了一个很好的技术途径。
[1]SMITH D R,PADILLA W J,VIER D C,et al.Composite medium with simultaneously negative permeability and permittivity[J].Phys Rev Lett,2000,84(18):4184-4187.
[2]ENOCH S,TAYEB G,SABOUROUX P,et al.A metamaterial for directive emission[J].Phys Rev Lett,2002,89(21):3902-3906.
[3]CHEN H T,PADILLA W J,ZIDE J M O,et al.Active terahertz metamaterial devices[J].Nature,2006,444:597-600.
[4]LANDY N I,SAJUYIGBE S,MOCK J J,et al.Perfect metamaterial absorber[J].Physical Review Letters,2008,100(20):207402.
[5]CUBUKCU E,AYDIN K,OZBAY E.Subwavelength resolution in a two-dimensional photonic-crystal-based superlens[J].Phys Rev Lett,2003,91:207401-207404.
[6]SCHURIG D,MOCK J J,JUSTICE B J,et al.Metamaterial electromagnetic cloak at microwave frequencies[J].Science,2006,314(5801):977-980.
[7]LAILA D,SUJITH R,SHAMEENA V A,et al.Complementary split ring resonator-based microstrip antenna for compact wireless applications[J].Microwave and Optical Technology letters,2013,55(4):814-816.
[8]LANDY N I,BINGHAM C M,TYLER T,et al.Design,theory,and measurement of a polarization-insensitive absorber for terahertz imaging[J].Phys Rev,2009,B79:125104-125109.
[9]LI M H,YANG H L,HOU X W,et al.Perfect metamaterial absorb with dual bands[J].Progress in Electromagnetics Research,2010,108:37-49.
[10]LUO H,WANG T,GONG R Z,et al.Extending the bandwidth of electric ring resonator metamaterial absorber[J].Chin Phys Lett,2011,28(3):034204.
[11]WAKATSUCHI H,PAUL J,GREEDY S,et al.Cut-wire metamaterial design based on simplified equivalent circuit models[J].IEEE Trans Antennas Propagation,2012,60(8):3670-3678.
