非饱和土渗流特性对库岸边坡稳定性的影响

刘博，李江腾，王泽伟，廖峻，郝瑞卿

(中南大学 资源与安全工程学院，湖南 长沙，410083)

自从意大利瓦利昂水库滑坡事件之后，各国学者开始意识到水库库岸边坡的稳定性对于工程建设和正常运营有着重大意义。水库库岸滑坡往往发生在水库的库水位发生急剧变化的阶段，在日本约60%的水库滑坡发生在水位骤降时，40%发生在水库上升时。中村浩之等[1]对日本水库滑坡进行分析与调研后认为引起库岸边坡滑坡的主要是由边坡岩土体浸水、库水位的急剧下降以及降雨等因素引起。钟立勋[2]调查了Rasevelt 湖附近地区1941—1953年发生的一些滑坡，发现49%发生在1941—1942年的蓄水初期，30%发生在水位骤降10～20 m 的情况下，其余为发生在其他时间的小型滑坡，由此可见库水位的涨落对于库岸边坡的稳定性有着重大的影响，很多学者对此进行了大量研究，如郑颖人等[3]基于Boussinesq 方程研究了库水下降过程中地下水浸润面的位置，并在此基础上对比分析了根据经验概化浸润面位置进行的稳定性所得出的误差及各种因素对库水边坡稳定性的影响。廖红建等[4]在基于Geo-slope软件的基础上，对不同渗透率和处于不同库水位下降条件下的边坡稳定性进行了对比分析，并得出了渗透率和库水下降速度对边坡稳定性的影响规律。Berilgen[5]在考虑土体模型为 hardening soil模型的基础上，分析了边坡稳定性和变形性能受土体渗透系数、水位下降速度、水位下降高度比等因素的影响。黄茂松等[6−7]在考虑土的应变软化效应和非饱和土强度准则的基础上分析了非稳定非饱和渗流对土坝稳定性的影响。年廷凯等[8]基于abaqus软件分析了基质吸力对于边坡稳定性的影响。影响水库库岸边坡稳定性的因素有很多，如库水位下降速度、下降高度、降雨条件、土体的饱和渗透系数、浸润线位置、基质吸力等。一些研究者[9]对这些因素对库岸边坡稳定性的影响进行了大量分析，但是，对于土体的非饱和渗流特性对库岸边坡稳定性的影响分析很少，为此，本文作者通过采用Fredlund和Xing提出的非饱和土水土特征曲线估算方程[10]对库岸边坡稳定性受非饱和渗流特性的影响进行分析。

1 计算原理

1.1 土水特性曲线估算公式

土水特性曲线是描述非饱和土体中土体含水量和基质吸力关系的曲线，这一曲线通常由实验得到的数据与某一估算公式进行耦合确定公式中的待定常数而获得。现在常用的估算公式主要有Brooks等提出的公式、Van Genuchten公式和Fredlund和Xing提出的估算公式[10]，其中前两者缺乏理论基础，属于经验公式，也不能准确地模拟整个基质吸力范围内的非饱和土含水量；而Fredlund ＆ Xing估算公式则是以毛细定律为理论基础，认为土体中孔隙的半径与负孔压成反比，结合土体孔隙的概率分布公式推导得来，所以，该估算公式更加科学，并且适用更加广泛的土体情况和更广的基质吸力范围，其待定参数的物理意义相对于前两者也更加明确。Fredlund ＆ Xing估算公式如下：

其中：wφ为水的体积分数；CΨ为函数的修正项，其使得水的体积分数在基质吸力趋向于1 GPa时趋向于0；sφ为饱和水的体积分数；e为自然数；Ψ为负孔隙水压力；iΨ为曲线拐点体积分数对应的基质吸力；φi为曲线拐点水的体积分数；Cr为对应于残余水的体积分数的基质吸力有关常数；ks为经过拐点的函数切线的斜率；a，m和n为拟合参数，通过与实验数据对比确定，但这些参数具有一定的物理含义。由Fredlund ＆ Xing估算公式推导出的非饱和土渗透系数函数为[11]

其中：kw为非饱和土的渗透系数；ks为饱和土的渗透系数；kr为相对渗透系数；y为负孔隙水压力算法的虚拟变量；j为函数描述的最小负孔隙水压力；N为函数描述的最大负孔隙水压力；φ′为方程的起始值。

将由式(1)～(7)计算得到非饱和土渗透系数代入土体的渗流公式中便可以得到非饱和土的渗流场变化。由于非饱和土的渗透系数与土体水的体积分数有关，在计算过程中，非饱和土体的渗透系数是不断调整变化的。

1.2 流固耦合计算原理

在流固耦合计算过程中，认为土坡内水的流动服从Darcy定律，其表达式为

式中：vw为流体的速度；s为饱和度；np为孔隙率；ρw为水的密度；uw为孔隙水压力；k为渗透系数，该渗透系数既可以为饱和土的渗透系数，也可以为非饱和土渗透系数。

土体内流体的连续性方程如下：

式中：n为边界外法线方向向量。

渗流场与应力场的耦合采用的是基于非饱和土有效应力的BIOT固结理论。

1.3 边坡稳定性计算

通过流固耦合计算过程可以得到边坡在某一时刻的渗流场与应力场，在此基础上对边坡稳定性的分析计算采用的是由 Zienkiewicz等[12]提出的有限元抗剪强度折减法，其相对于求解安全系数的极限平衡法具有不需要假定滑动面，适用于复杂地质条件和表面形态边坡的优势，现已得到广泛推广和应用。该方法的强度折减方程如下：

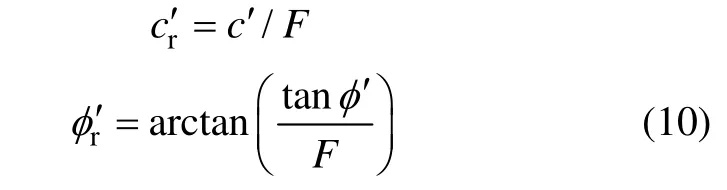
式中：cr′和rφ′为折减后的强度参数；c′和φ′为实际强度参数；F为折减系数。对边坡稳定性的计算应该是在单纯的静力条件下进行的，在折减计算过程中，将渗流场设定为不变值，这样计算得到的才是渗流发生至某一时刻的安全系数。

2 模型计算及分析

2.1 计算模型

为研究非饱和土渗流参数对库水下降条件下库岸边坡稳定性的影响，建立如图1所示的均质土边坡的平面模型。边坡的高度为7 m，坡度为1:3，土体的强度参数参照文献[13]中的取值：c′=10 kPa，φ′=20°，土体密度ρ=2 t/m3，弹性模量和泊松比分别为E=0.1 GPa，μ=0.3。边坡土体在饱和状态下的渗透率取为ks=1×10−4cm/s。非饱和土的渗流特性主要反映其土水饱和曲线的形式，在Fredlund和Xing提出的估算公式中存在3个待定参数，并且这3个参数对曲线的影响个不相同：a可以视为土体的进气值，m与土体的剩余含水量相关；n决定了随着基质吸力增大土体含水量变化的速度。为此，参照文献[10]，选取a为1，10，20，40和70 kPa，m取0.5，1.0和1.5，n取1.2，2.0，4.0和10.0，所得土体的土水特征曲线如图2所示。其中图2(a)所示为当m=1和n=4及不同a时的土水特征曲线；图2(b)所示为当a=5 kPa和n=4及不同m时的土水特征曲线；图2(c)所示为当a=5 kPa和m=1及不同n时的土水特征曲线。相对渗透率kr随基质吸力的变化曲线见图3。

图1 边坡数值计算模型Fig. 1 Numerical calculation model of slope

为了实现库水位下降的条件下库岸边坡的模拟，本文通过Fortran语言编写用户子程序对abaqus软件进行二次开发，从而实现了边坡迎水面的边界条件随时间而变化。本文模拟了库水位以1 m/d的速度匀速下降的情况。

2.2 参数a对边坡稳定性的影响

Fredlund ＆ Xing推导的估算公式中参数a能在一定程度上反映非饱和土体的进气值(得到曲线的实际进气值略小于a)，这一参数显著影响了非饱和土的渗流特性。由图2(a)可以看出：当a较大时，曲线的起始水平段变长，并且整个曲线趋于平缓，即饱和度随基质吸力增加平缓降低，这一影响趋势同样也反映在了相对渗透系数随基质吸力变化的曲线上。图 3(a)中的相对渗透系数也有相同的变化趋势。参数a对非饱和土渗流特性的影响将反映在土体的渗流场变化中，在库岸边坡稳定性分析中，人们最关心的影响因素之一就是随着库水位下降土体中浸润线的位置。浸润线反映了坡体中孔隙水压力的分布与超孔隙水压力的耗散情况，可以间接地反映边坡的稳定性，对于土体参数及其他外部边界条件相同的边坡，浸润线的位置越高，边坡的稳定性越差。对于本例中的模型，当库水位以1 m/d的速度下降7 m后，不同a对应的浸润线位置如图4所示。从图4可以看出：随着a的增大，浸润线位置会显著下降，即土体中超孔隙水压力的耗散程度越大，边坡越趋于稳定。对比文献[8]可知：a对浸润线的影响与饱与土渗透系数对浸润线的影响相类似。

图2 a，m和n对土水饱和度的影响Fig. 2 Influence of a, m and n on soil-water saturation

安全系数F是反映边坡稳定性的直接指标，图5所示反映了不同a对库水位下降条件下边坡安全系数的影响。由图5可以看出：当a大于20 kPa时，边坡的安全系数随着水位下降是先减小后增大；当a小于20 kPa时，安全系数随着水位下降将一直下降；参数a对安全系数的影响随着水位下降深度的增加而不断加大，在水位下降7 m后，a=70 kPa时的安全系数比a=5 kPa时的大23.14%。

图4 a对土坡内浸润线的影响Fig. 4 Influence of a on phreatic line

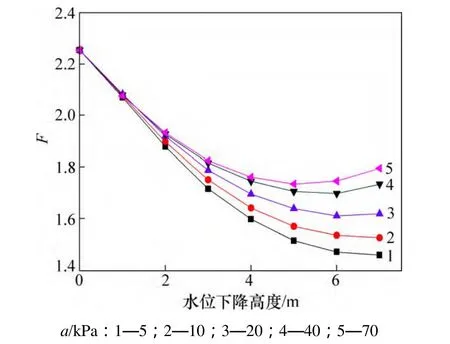
图5 a对边坡安全系数F的影响Fig. 5 Influence of a on factor of safety of slope

2.3 参数m对边坡稳定性的影响

参数m对非饱和土剩余含水量起控制作用。从图2(b)可以看出：当m越大时，非饱和土的剩余饱和度越低。而从图3(b)可见：当m=0.5～1.5时，m对非饱和土的渗透系数影响很小。m对浸润面位置的影响如图6所示。从图6可以看出：m对于边坡浸润面的影响也非常小。图7所示为m对该库岸边坡安全系数的影响。由图7可知：当m较小时对应的安全系数略大于m较大时的安全系数，即非饱和土的剩余渗透系数对库岸边坡的稳定性影响不显著；当库水位下降7 m后，最大安全系数仅比最小安全系数大2.6%。

2.4 参数n对边坡稳定性的影响

n是控制非饱和土土水特性曲线拐点斜率的参数。由图 2(c)可得：n越小，土水特性曲线越平缓；反之，则曲线越陡。同时，n减小也使得进气值减小。由图3(c)可得：当n较小时，非饱和土的相对渗透系数会随着基质吸力更快地减小为一个较小值；n=4和n=10的相对渗透系数曲线很相近，可以认为当n>4时，其对相对渗透系数曲线的影响很小。n对浸润面和安全系数的影响如图8和图9所示。由图8可得：当n为4和10时，两者的浸润面在斜坡段基本重叠。以n=10 时的浸润线作为参照可以发现：随着n减小，其对浸润面位置的影响越来越大，而不是均匀变化的，这一趋势与相对渗透系数曲线相同，也同样反映在边坡的安全系数中，其中最大安全系数比最小安全系数大7.5%。

图6 m对土坡内浸润线的影响Fig. 6 Influence of m on phreatic line

图7 m对边坡安全系数F的影响Fig. 7 Influence of m on factor of safety of slope

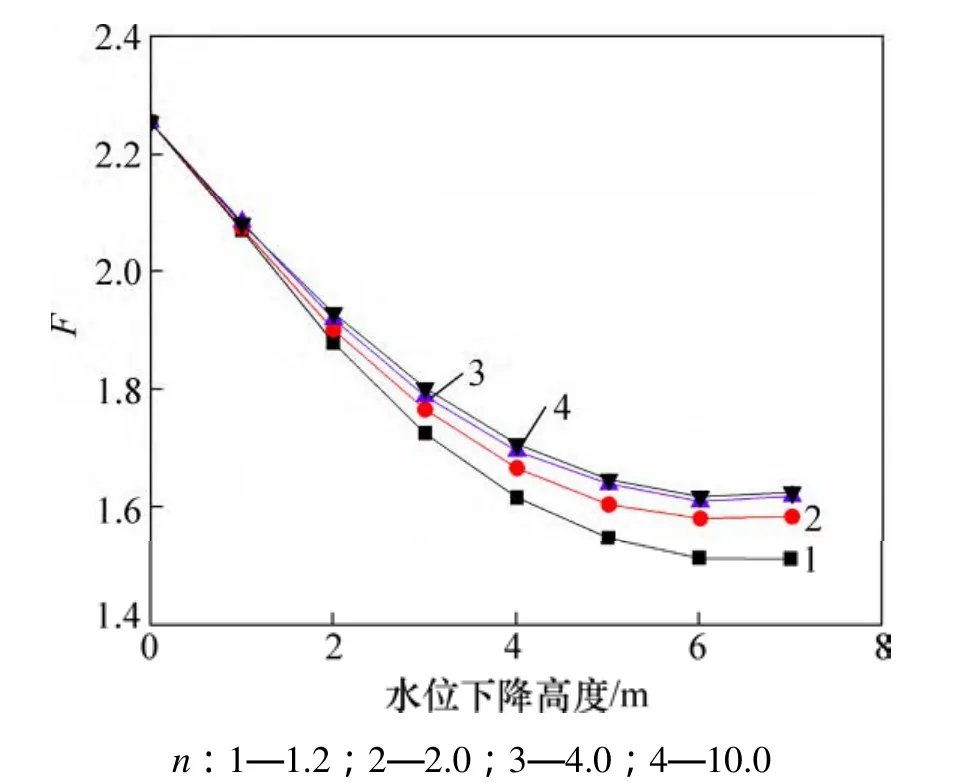
图9 n对边坡安全系数F的影响Fig. 9 Influence of n on factor of safety of slope

2.5 结果分析

由上述计算结果可看出库岸边坡的安全系数、浸润面位置与非饱和土的相对渗透系数与基质吸力关系曲线之间存在相关性。相对渗透系数与基质吸力关系曲线可以看作由2个水平段和1个倾斜段组成，起始水平段反映了非饱和土的进气值，当该段曲线越长时，土体的进气值越大；而中间的倾斜曲线反映了随基质吸力的增大，土体由饱和渗透率变化至剩余饱和度条件下非饱和渗透率的过程，曲线越斜率越大，则这一变化过程越快。曲线最后的水平段反映了剩余饱和度条件下的非饱和土渗透率。当初始水平段越短，同时倾斜段变化率越大时，因为土体的进气值较小，随着库水位下降，边坡中的饱和土将很快失水变为非饱和土，随着库水位进一步下降，土体中的基质吸力进一步增大。由于曲线中倾斜段变化率大，非饱和土区域的渗透系数将迅速减小，使得水在这一区域渗流速度大幅度下降，大部分的水必须从饱和区域出渗流出边坡，从而影响了边坡整体的渗流场，浸润面维持在一个较高的水平；随着浸润面下降，难以渗流的非饱和区域将增大，从而进一步影响渗流速度，使得浸润面更加难以下降。而较高的浸润面位置反映了边坡中的超孔隙水压力处于一个较高水平，这将减小边坡土体中的有效应力，从而使得边坡的稳定性下降。反之，当起始水平段越长即进气值越大时，曲线倾斜段越平缓，非饱和渗透系数相对基质吸力减小较慢，从而对整个边坡内部的渗流速度的影响较小，这有利于超孔隙水压力的耗散和浸润面下降，从而也更有利于边坡的稳定。

3 结论

(1) 非饱和土的相对渗透系数与基质吸力关系曲线对库水位下降条件下库岸边坡稳定性有重要影响。总体来说，曲线的起始水平段越短，倾斜段越陡，土坡内浸润面位置将越高，越不利于边坡稳定性。该曲线受a，m和n这3个参数不同程度的影响。

(2) 参数a与非饱和土的进气值相关，对非饱和土的相对渗透系数与基质吸力关系曲线中的起始水平段长度影响显著；a越小，浸润面位置越高，边坡稳定性越差。

(3) 参数m与非饱和土的剩余饱和度有关，但是，其取值对相对渗透系数与基质吸力关系曲线影响很小，其对浸润面和边坡稳定性的影响也很小。

(4) 参数n和相对渗透系数与基质吸力关系曲线的初始水平段长度和倾斜段的变化率都相关，随着n变化，其对边坡稳定性和浸润面位置的影响表现出非线性，随n减小，其影响程度将越来越大。

(5) 对库岸边坡稳定性产生重要影响的因素不只是饱和土渗流特性及库水位下降速度等因素，土体的非饱和渗流特性对边坡的稳定性也有重要影响。

[1]中村浩之, 王恭先. 论水库滑坡[J]. 水土保持通报, 1990,10(1): 53−64.Nakamura K, WANG Gongxian. On reservoir landslide[J].Bulletin of Soil and Water Conservation, 1990, 10(1): 53−64.

[2]钟立勋. 意大利瓦依昂水库滑坡事件的启示[J]. 中国地质灾害与防治学报, 1994, 5(2): 77−84.ZHONG Lixun. Enlightenments from the accident of vaiont landslide in Italy[J]. The Chinese Journal of Geological Hazard and Control, 1994, 5(2): 77−84.

[3]郑颖人, 唐晓松. 库水作用下的边(滑)坡稳定性分析[J]. 岩土工程学报, 2007, 29(8): 1115−1121.ZHENG Yingren, TANG Xiaosong. Stability analysis of slopes under drawdown condition of reservoirs[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(8): 1115−1121.

[4]廖红建, 盛谦, 高石夯, 等. 库水位下降对滑坡体稳定性的影响[J]. 岩石力学与工程学报, 2011, 24(7): 2071−2077.LIAO Hongjian, SHENG Qian, GAO Shihang, et al. Influence of drawdown of reservoir water level on landslide stability[J].Chinese Journal of Rock Mechanics and Engineering, 2011,24(7): 2071−2077.

[5]Berilgen M M. Investigation of stability of slopes under drawdown conditions[J]. Computers and Geotechnics, 2007,34(2): 81−91.

[6]黄茂松, 贾苍琴. 考虑非饱和非稳定渗流的土坡稳定分析[J].岩土工程学报, 2006, 28(2): 202−206.HUANG Maosong, JIA Cangqin. Stability analysis of soil slopes subjected to unsaturated transient seepage[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 28(2): 202−206.

[7]HUANG Maosong, JIA Cangqin. Strength reduction FEM in stability analysis of soil slopes subjected to transient unsaturated seepage[J]. Computers and Geotechnics, 2009, 36(1/2): 93−101.

[8]年廷凯, 万少石, 蒋景彩, 等. 库水位下降过程中土坡稳定强度折减有限元分析[J]. 岩土力学, 2010, 31(7): 2264−2269.NIAN Tingkai, WAN Shaoshi, JIANG Jincai, et al. Finite element analysis of slope stability under drawdown conditions by strength reduction technique[J]. Rock and Soil Mechanics,2010, 31(7): 2264−2269.

[9]蒋中明, 曾铃, 付宏渊, 等. 降雨条件下厚覆盖层边坡的渗流特性[J]. 中南大学学报(自然科学版), 2012, 43(7): 2782−2788.JIANG Zhongming, ZENG Ling, FU Hongyuan, et al. Seepage characteristics of thick coating slope in raining condition[J].Journal of Central South University (Science and Technology),2012, 43(7): 2782−2788.

[10]Fredlund D G, Xing A. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(3): 521−532.

[11]Krahn J. Seepage modeling with SEEP/V: An engineering methodology[R]. Alberta, Canada: GEO-SLOPE International Ltd, 2004: 45, 51−52.

[12]Zienkiewicz O C, Humpheson C, Lewis R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique, 1975, 25(4): 671−689.

[13]Lane P A, Griffiths D V. Assessment of stability of slopes under drawdown conditions[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(5): 443−450.