面向类旋涡星系盘有效厚度的获取及图像处理方法∗

胡 涛 彭秋和

(1上海大学自动化系上海200072)(2中国科学院天体结构与演化重点实验室昆明650011)(3南京大学天文与空间科学学院南京210093)

面向类旋涡星系盘有效厚度的获取及图像处理方法∗

胡 涛1,2†彭秋和3

(1上海大学自动化系上海200072)(2中国科学院天体结构与演化重点实验室昆明650011)(3南京大学天文与空间科学学院南京210093)

面向类(face-on)旋涡星系盘的有效厚度或标高不能通过表面亮度测光的方式测量.为了获得面向类旋涡星系盘的厚度参数,将基于三维星系盘引力势Poisson方程在等角对数螺旋型物质密度扰动情形下的解,运用一种解析法对面向类旋涡星系盘的标高进行测算.为了去除星系核球的光污染而获得旋臂最内点位置(r0)的重要参数,使用了在星系观测图像中扣除双成份(盘+核球)测光模型的图像处理方法.通过对旋涡星系相关结构参数的拟合测量,各得到了一个普通旋涡星系(S)与棒旋星系(SB)的有效厚度与相关参数,并给出了它们的球盘比(rb/rd)和星系盘的标长与厚度之比(rd/H).采用这种在观测图像中扣除双成份测光模型的方法,将更容易看清旋臂结构的最内端,因而这里获得的禁区半径r0的数值往往比从原星系图像上直接测量的数值要小,获得的星系盘有效厚度将更薄.

星系:盘,星系:基本参数,星系:旋臂,星系:结构

1 引言

星系盘的标高也常称为有效厚度或等效厚度,是三维星系盘模型中非常重要的关键参数.根据盘状星系的观测图像,可按照其星系盘的形状,即面向的程度分为两种类型(亦可根据侧向程度分类):面向盘和非面向盘,其中的非面向盘还包括侧向(edge-on)盘和介于面向与侧向盘之间类型的非侧向盘.

盘状星系包括旋涡星系与透镜星系,其中旋涡星系的数量占主导.早在1981年,van der Kruit等[1]就给出了测量侧向旋涡星系盘厚度参数的侧向测光法,即根据侧向盘表面亮度的z方向分布,对星系盘的标高进行测算;基于此测量方法,van der Kruit等[1−4]对7个侧向旋涡星系(NGC 891,NGC 4013,NGC 4217,NGC 4244,NGC 4565,NGC 5023,以及NGC 5907)盘的标高进行了研究和测算.测光法也是目前国际上对侧向星系盘有效厚度测量的主流方法.

尽管测光法对侧向星系盘标高的获取非常有效,但是它对面向类旋涡星系盘标高的测量却爱莫能助.在同一时期,文献[5-8]研究了三维星系盘引力势Poisson方程在等角对数螺旋型物质密度扰动情形下的渐近解,在此基础上Peng[9]创新地提出一种简洁地获得面向类旋涡星系盘有效厚度的解析法,解决了国际上难以测算面向类旋涡星系盘厚度的难题.Zhao等[10]基于Peng[9]的近似解,改进并推出了星系盘厚度的数值计算严格解.Zhao等[10]的严格解与Peng[9]的近似解相差不大,两者的差异小于9%[11].基于Peng[9]的方法,Ma等[12−13]对旋涡星系盘做了大样本的实测工作;基于Zhao等[10]的方法,Zhao等[10]与Hu等[11,14−16]对旋涡星系盘等效厚度以及旋涡结构的相关参数进行了研究与测定,Hu等[17]提出了测量面向类旋涡星系质光比的新方法.

Peng[9]或Zhao等[10]的方法都是基于获得旋臂结构相关参数的基础上,将计算得出旋涡星系的标高;这就涉及到旋臂禁区半径(r0)的获取,即旋臂趋向星系中心时最内点的位置的确定.然而,由于核球的光污染,禁区半径很难准确判定.本文针对这个难点,采用在星系观测图像上直接扣除星系盘与核球双成份模型的方法,来确定旋臂禁区半径的大小,从而减小了由于核球的光污染而引入的人为判定带来的偏差.本文中我们测算了两个面向类旋涡星系的标高及旋臂结构参数:选取了普通旋涡星系(S)与棒旋星系(SB)各一个,其哈勃参数都为T=3,既不偏早型也不偏晚型,哈勃参数选择居中;并且它们的星系盘倾角都相对较小,其倾角对测光模型的参数拟合影响较小.在此类型中(S与SB;T=3;星系盘倾角较小),这两个星系是随机选取的.

2 面向类旋涡星系盘有效厚度的测算方法

Peng等[5−9]采用了与观测数据相符合的三维有限厚度星系盘的物质密度分布模型:

其中H为星系盘的有效厚度或等效厚度(标高通常定义为Hsc=0.5H).σ(r,ϕ)为星系盘的面密度,包含两种成份:旋臂结构面密度σs(r,ϕ,t)与基盘密度σ0,如果σs(r,ϕ,t)采用等角对数螺线的形式[5−8,18],则可以推导出在等角对数螺线型物质密度扰动情形下的引力势Poisson方程为[5−8]:

在z=0处,方程(2)的解为[5−9]

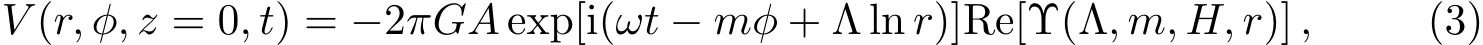
其中

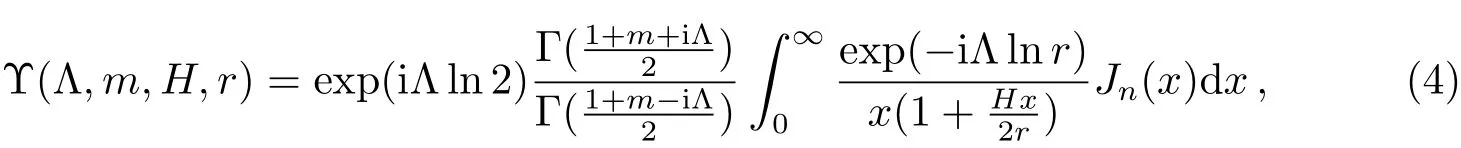
这里Γ(x)与Jn(x)分别为Gamma函数与Bessel函数.m与Λ分别为旋臂的数目与紧卷参数,r为星系盘的半径.

(3)式的近似解为[7−8]:

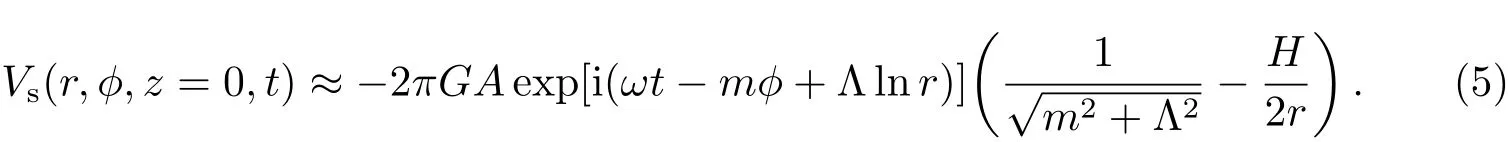
根据密度波理论的思想,当扰动引力势趋近为零时,即(5)式约等于零时,旋臂消失.Peng[9]认为旋涡星系的旋臂结构不能存在于旋臂禁区半径(旋臂最内点位置的半径)区域内(r＜r0),即当r=r0时旋臂结构消失,根据(5)式,此时旋涡星系盘的有效厚度为[9]:

3 图像处理方法

从上述的旋涡星系盘有效厚度的测算方法可以看出,如果得到了旋臂的禁区半径r0、紧卷参数Λ(或切向角)和旋臂数目m,就可以通过(6)式推算出旋涡星系盘的厚度.

3.1 禁区半径r0的获取

禁区半径r0是旋臂向内延伸的截止点(或最内点)到星系中心的距离.测量出较为准确的r0是算出星系盘有效厚度的关键.通常可以在星系的观测图像中直接测算出r0的数值,即旋臂最内点与星系中心的直线长度.可以在星系图像的显示软件中调节图像的亮度与灰度,而判断出旋臂最内点的位置.但往往因为核球的光污染,只能判断出旋臂最内点的大致方位.这种测量常常带有人为的习惯与主观因素,不同的人测量会给出不同的结果,并且测量的差异会随着星系图像质量变差而变得更大.

面向类旋涡星系的表面亮度模型是表面亮度均匀分布的测光模型,即在同一半径处表面亮度数值相等.在相同位置处,由于旋臂的实际亮度大于星系均匀测光模型的亮度,可以在面向类旋涡星系观测图像上直接扣除此星系的表面亮度图像,因此星系图像中剩余的部分将只会是明亮的、突出的旋臂,从而可以较为准确地测量旋臂最内点的位置,得到相对精确的r0.

3.2 面向类盘状星系表面亮度的拟合

3.2.1 基本模型

面向类盘状星系的表面亮度模型是星系盘+核球双成份模型.其中星系盘成份为[19]

而核球成份遵循着r1/4的幂减律[20−22]

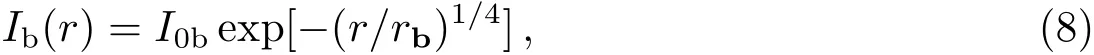
其中,rd与rb分别为星系盘与核球的标长.

通过(7)式与(8)式就可以对面向类星系盘的表面亮度进行拟合,如果采用星等做表面亮度的单位,将星系盘+核球双成份进行叠加,即(7)式与(8)式的叠加,得到总的星系盘表面亮度为:t

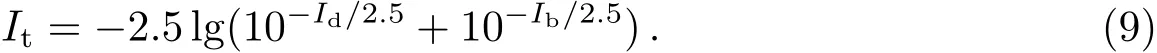
3.2.2 模型拟合

这里选取的星系图像来自Sloan巡天数据(SDSS),其星系图像文件为FIT格式,图像中像素的流量值F与(9)式有如下的关系:

其中,Flux20为星系图像头文件中的一个参量,其大小为星系图像中20 mag处的像素流量值,并且将20 mag归算为图像中的参照点.因此,根据(10)式就可以得到星系的盘+核双成份模型的图像F.在原星系图像中扣除模型图像F后,余下的就为剩余旋臂图像.主要的模型拟合步骤有:

(1)相对于星系中心,在不同的半径处,取宽度为Δr的光圈(环带),测算出光圈中的像素流量的平均值;

(2)对上述不同半径处光圈中的像素流量的平均值进行盘+核双成份测光模型拟合,得到相关参数;

(3)根据(10)式,得到双成份测光模型的流量值F;

(4)对模型图像中的星系中心的处理:由于星系中心r→0时,所得到的F值会趋向极大,所以要对星系中心点进行1 pixel×1 pixel面积的积分处理;

(5)由于视宁度因素的影响,整个模型图像要卷积一个相应的点扩散函数(PSF)图像文件.

3.3 旋臂紧卷参数Λ的获取

在星系图像中,以旋臂禁区半径r0处的位置为起点,通过旋臂的形状来拟合旋臂的等角对数螺线,从而获得旋臂的紧卷参数Λ,以及切向角等参数.

旋臂在面向类星系盘中的等角对数螺线为:

其中,(r,Θ)为星系盘的极坐标,(r0,Θ0)是旋臂禁区半径起始点的极坐标.旋臂的切向角为:

3.4 实测步骤

在对面向类旋涡星系的实测中,总结出以下的主要步骤:

(1)对面向类旋涡星系盘进行星系盘+核球的双成份测光拟合,得到其表面亮度模型的图像F;

(2)模型图像F卷积PSF,得到图像Fp;

(3)在原星系观测图像中扣除模型图像Fp后,得到剩余旋臂图像;

(4)调节程序的亮度与灰度参数使剩余旋臂图像显示得更加清晰;

(5)测量旋臂禁区半径起始点的位置,得到它的极坐标(r0,Θ0);

(6)以(r0,Θ0)为初始点,沿旋臂向外延伸的中心线采样取值;

(7)根据采样点的坐标,在剩余旋臂图像中拟合旋臂的等角对数螺旋线,得到紧卷参数Λ和切向角ϑ;

(8)通过(6)式,计算出旋涡星系盘的有效厚度H.

4 测算结果

本文给出了两个旋涡星系盘的有效厚度H及其旋涡结构的相关参数.这里,普通旋涡星系与棒旋星系各选一个,其哈勃参数都为T=3,哈勃参数选择居中,既不偏早型也不偏晚型.它们的星系盘倾角都相对较小,为面向类星系,其倾角对测光模型的参数拟合影响较小.表1中列出的是这两个旋涡星系在g与r波段中的星系盘+核球双成份测光模型,并给了它们的球盘比(rb/rd,第7列).将测光模型从星系的原观测图像中扣除后,就可以得到剩余旋臂图像(详见图1中的(e)与(k)图).表2中给出了这两个星系的有效厚度H、禁区半径r0、旋臂的紧卷参数Λ、切向角ϑ以及星系盘的标长与厚度之比(rd/H)等参数.

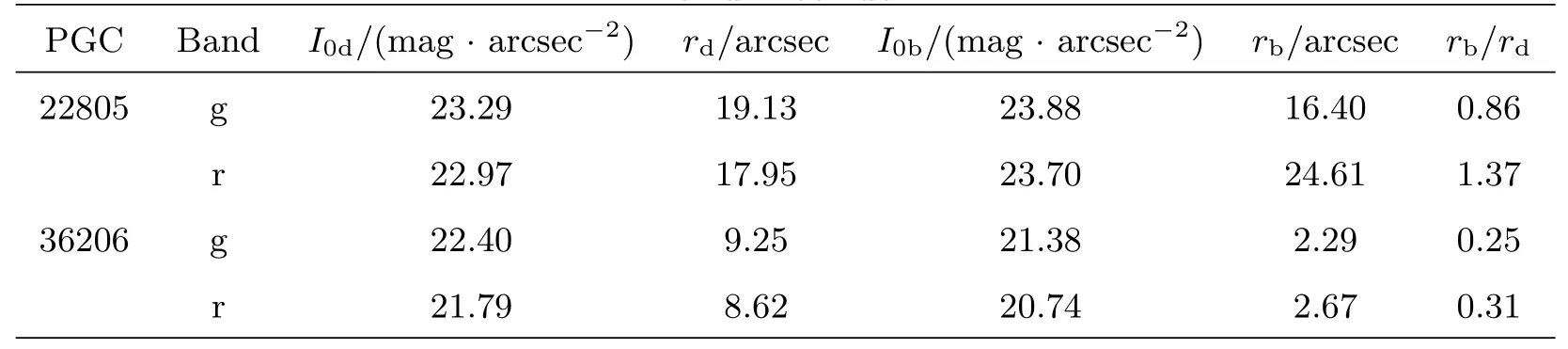
表1 面向类旋涡星系PGC22805与PGC36206的星系盘+核球双成份测光模型(g与r波段)Table 1 The disk+bulge decomposition models of PGC22805 and PGC36206 in gand r-bands

表2 面向类旋涡星系PGC22805与PGC36206的有效厚度及旋臂结构的相关参数Table 2 The disk thickness H and spiral structures of PGC22805 and PGC36206

图1给出的是面向类旋涡星系PGC22805在g与r波段的星系盘+核球双成份表面亮度模型的图像,以及相关图像处理的实例.图中的(a)与(g)图是其在g与r波段的双成份表面亮度模型的图像;(b)与(h)图为其在g与r波段点扩散函数PSF的图像;考虑视宁度的因素,(c)与(i)图显示的是PGC22805在g与r波段的表面亮度模型卷积PSF后的图像,记为Fp;图中的(d)与(j)图给出了PGC22805在g与r波段的原观测图像;(e)与(k)图给出的是剩余旋臂图像,即PGC22805在g与r波段原观测图像扣除Fp后的结果.图1中的(f)与(l)图给出的是对PGC22805旋臂结构等角对数螺线的拟合.

图1 PGC22805的相关图像(g与r波段).其中,(a)与(g)图:PGC22805在g与r波段的星系盘+核球双成份表面亮度模型的图像;(b)与(h)图:PGC22805在g与r波段点扩散函数PSF的图像;(c)与(i)图:PGC22805在g与r波段的表面亮度模型卷积PSF后的图像,记为Fp;(d)与(j)图:PGC22805在g与r波段的观测图像;(e)与(k)图:PGC22805在g与r波段观测图像扣除Fp后的剩余旋臂图像;(f)与(l)图:PGC22805在g与r波段旋臂结构的等角对数螺线拟合.本文中的星系观测图像取自于Sloan巡天数据(SDSS).Fig.1The images for PGC22805 in g-and r-bands.(a)and(g):The disk+bulge decomposition models of PGC22805 in g-and r-bands;(b)and(h):The PSF images of PGC22805 in g-and r-bands;(c)and(i):The Fpimages of the disk+bulge decomposition models convolving the PSFs in g-and r-bands;(d)and(j):The observed images of PGC22805 in g-and r-bands;(e)and(k):Residual spiral patterns after the Fpimages have been subtracted from PGC22805 images in g-and r-bands;(f)and(l):Fitting patterns of PGC22805 spiral arms in g-and r-bands.In this work,the observed images are taken from SDSS(Sloan Digital Sky Survey).

图2给出的是另一个面向类旋涡星系PGC36206在g与r波段的相关图像,其中包括:原观测图像、扣除双成份表面亮度模型后的剩余旋臂图像以及旋臂的等角对数螺线的拟合曲线.

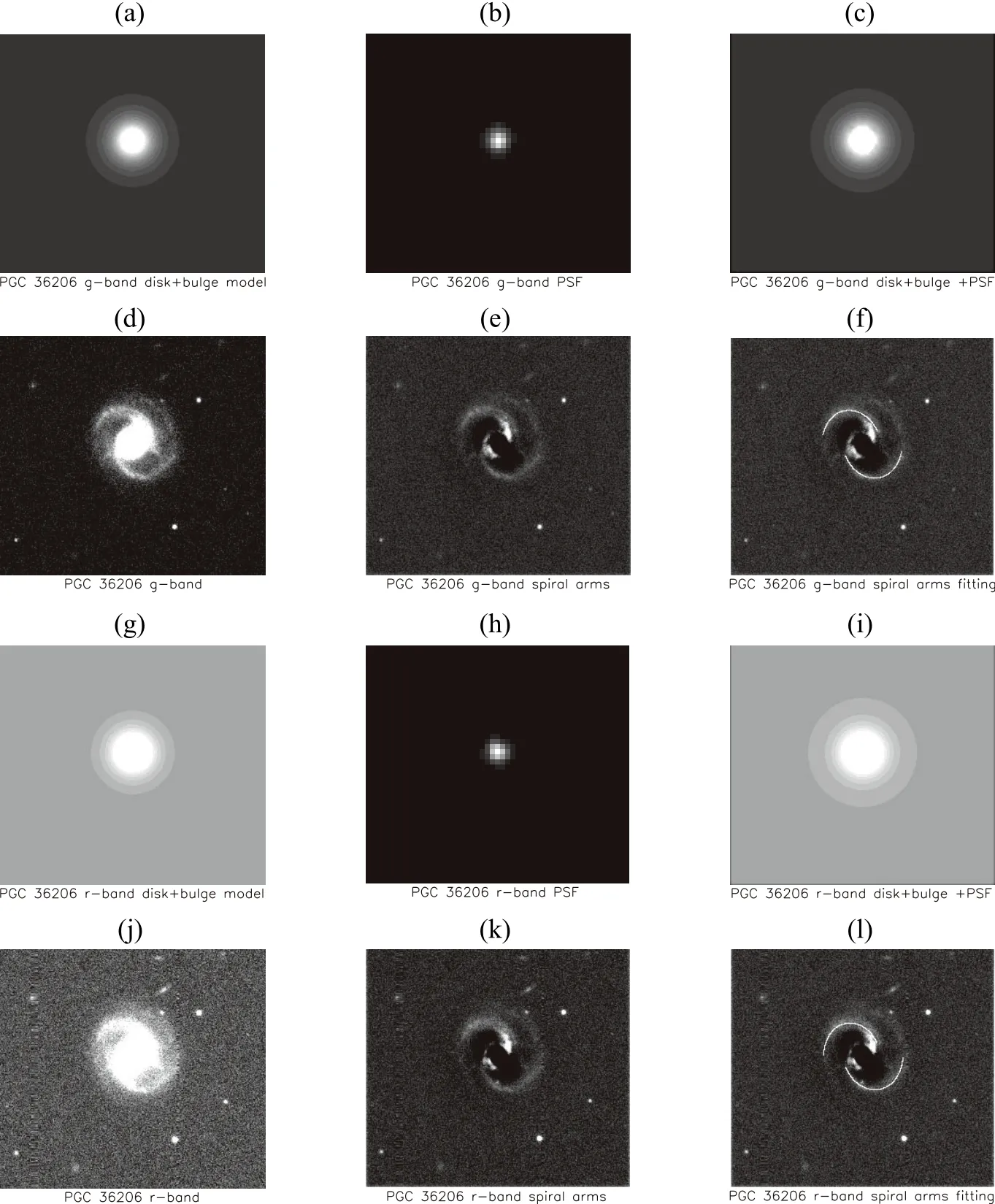
图2 与图1的结构布局一致,给出的是PGC36206的相关图像Fig.2 Same as in Fig.1,but for PGC36206

5 结论与讨论

Peng[9]的方法用在银河系和M31标高的测量中,得出的结果与国际上给出的数值一致,是一种非常实用的测量非侧向旋涡星系盘标高的有效方法.表3中列出的是已有的银河系与M31星系盘参数,其中第6列给出的是使用Peng[9]方法得到的银河系与M31的有效厚度,与第5列做对比可以看出:使用Peng[9]方法所得到的结果与国际上已有的结论基本一致.

由于SDSS中g与r波段的星系图像较为清晰,本文中选用的星系图像为g波段与r波段.从图1～2可以看出,旋涡星系的旋臂结构总体而言是较为清晰和对称的.但由于核球的光污染,旋臂向内截止点的位置不易确定,由于人的主观因素,不同的人测量往往结果会偏差较大.如果在原星系观测图像上扣除其盘+核球双成份表面亮度模型,来判断旋臂最内点的位置,就能够减少由于核球的光污染而带来的测量偏差,从而可以得到相对准确的旋臂禁区半径.测量r0时目前还是用目测,由于不同波段观测图像质量的不同,对r0的测量会有系统性的影响,但如果采用双成份模型扣除法,即在残差图像中测量r0,在不同波段中的r0基本一致(在本文中为g与r波段),请详见图1～2.采用这种扣除表面亮度模型法,更容易看清旋臂结构的最内端,因此,这里获得的禁区半径r0的数值往往比从原星系图像上直接测量的数值要小.

判断星系盘+核球双成份模型的拟合是否较好的标准,是根据旋臂剩余图像中全部像素的总流量值的相对大小来判定的:双成份模型图像中的像素总流量应该与原观测图像中的总流量一致;因此,如果星系模型图像与原观测图像中的总流量之差ΔFt与原观测图像的总流量Ft的比值(取绝对值)较小,则双成份模型的拟合较好.表2中的第10列给出的是|ΔFt/Ft|的比值,其值都不大于10%.

表3 银河系与M31的星系盘有效厚度Table 3 The disk thickness of the Galaxy and M31

[1]van der Kruit P C,Searle L.A&A,1981,95:105

[2]van der Kruit P C,Searle L.A&A,1981,95:116

[3]van der Kruit P C,Searle L.A&A,1982,110:61

[4]van der Kruit P C,Searle L.A&A,1982,110:79

[5]彭秋和,黄克谅,黄介浩,等.天文学报,1978,19:182

[6]Peng Q H,Huang K L,Huang J H,et al.ChA,1979,3:290

[7]黄克谅,黄介浩,彭秋和.天文学报,1979,20:232

[8]Huang K L,Huang J H,Peng Q H.ChA,1980,4:228

[9]Peng Q H.A&A,1988,206:18

[10]Zhao Y H,Peng Q H,Wang L.ChJAA,2004,4:51

[11]Hu T,Peng Q H,Shao Z Y.ChJAA,2006,6:43

[12]Ma J,Peng Q H,Gu Q S.A&AS,1998,130:449

[13]Ma J,Zhao J L,Shu C G,et al.A&A,1999,350:31

[14]Hu T,Shao Z Y,Peng Q H.ChJAA,2006,6:175

[15]Hu T,Peng Q H,Zong H S.ChJAA,2007,7:579

[16]Hu T,Shao Z Y,Peng Q H.ApJ,2013,762:L27

[17]Hu T,Peng Q H,Zhao Y H.A&A,2006,446:L5

[18]Kennicutt R C,Hodge P.ApJ,1982,253:101

[19]Freeman K C.ApJ,1970,160:811

[20]de Vaucouleurs G.ApJ,1958,128:465

[21]de Vaucouleurs G.AJ,1959,64:397

[22]Simien F,de Vaucouleurs G.ApJ,1986,302:564

[23]Kuijken K,Gilmore G.MNRAS,1989,239:571

[24]Haywood M,Robin A C,Greze M.A&A,1997,320:428

Determination of Disk Thickness of Face-on Spiral Galaxies and Its Image Processing Method

HU Tao1,2PENG Qiu-he3

(1 Department of Automation,Shanghai University,Shanghai 200072)(2 Key Laboratory for the Structure and Evolution of Celestial Objects,Chinese Academy of Sciences,Kunming 650011)(3 School of Astronomy&Space Science,Nanjing University,Nanjing 210093)

It is uneasy to obtain the disk thickness of face-on spiral galaxies by measuring the galactic light distributions.Here we obtain the spiral galactic disk thickness based on an asymptotic expression of Poisson’s equation for a logarithmic perturbation of matter density in spiral galaxies.For measuring the key parameter of the innermost position of the spiral arm(forbidden radiusr0)freed from the contamination by the light of bulge,an improved image processing method is used in this study by subtracting a decomposition brightness model from the galactic observed image.On the basis of measuring some fundamental parameters of spiral structures,we obtain the disk thickness and some other parameters of two(types S and SB)face-on spiral galaxies,and their ratio parameters(rb/rdandrd/H)are also derived.By using this improved subtracted-method,it is easy to measure the forbidden radiusr0,which is smaller than that obtained from unsubtracted-method.

galaxies:disk,galaxies:fundamental parameters,galaxies:spiral,galaxies:structure

P157;

A

2014-04-11收到原稿,2014-07-14收到修改稿

∗国家自然科学基金项目(U1331103)以及中国科学院天体结构与演化重点实验室开放课题(OP201202)资助

†thu@shu.edu.cn