多星混合资料的定轨∗
2014-11-29王歆
王 歆
(1中国科学院紫金山天文台南京210008)(2中国科学院空间目标与碎片观测重点实验室南京210008)
多星混合资料的定轨∗
王 歆1,2†
(1中国科学院紫金山天文台南京210008)(2中国科学院空间目标与碎片观测重点实验室南京210008)
在空间目标光学观测资料定轨中常常会遇到多个目标的观测被标记为同一个目标的情况,由于包含了多个目标的数据,定轨过程无法收敛或者完全错误.从极大似然估计角度,采用EM(Expectation Maximum)方法提出一种将轨道改进和识别过程相互融合的处理方法,并在具体实现过程中给出一种稳健估计方法.数值模拟表明方法简便、有效、可行.
航天器,天体力学,方法:统计
1 引言
随着航天活动的深入开展与航天技术的发展,卫星编队越来越多地被采用,编队飞行目标在光学观测中会出现在临近天区.由于空间目标预报误差,在观测中往往会采用提前摆位等方式来进行空间目标的捕获,当目标先后经过视场时,由于视运动相近,以及光学观测干扰因素较多,实践中很难正确判断待捕获目标.对于大视场空间目标观测望远镜,编队飞行的目标甚至会同时出现在视场中,观测中也难以正确识别.
这种情况使得采集的观测资料中,虽然都按照预报进行了标记,但不同站圈实际上跟踪了不同的目标,形成了本文提出的多星混合资料,这里混合有“混淆”的含义.按照标记目标对这些资料进行轨道改进时,往往无法收敛.过去对于这类资料多采取人工处理,依赖经验并没有成熟的方法.现在观测能力与数量大幅度提高后,此类情况也大幅度增加,依赖人工已无法满足需求.即便采用轨道识别方法,对于编队目标由于目标过于接近而无法区分[1].如何自动处理这类资料是一个棘手的问题.
这个问题表面上可归为稳健估计的范畴,也就是将标记错误的资料作野值处理.然而该问题并不能简单处理,一方面从资料属性上只是属于两个目标,而并不是“坏”的观测;另一方面也无法确保正确标记的观测量占到多数,因此单纯从稳健估计角度是不能解决问题的.
本文从另一个角度对问题进行了细致的分析,虽然资料中可能包含了多个目标,但根据标记的目标代号,通常可以知道资料属于哪一组编队目标,而编队的目标集通常是已知的.在目标集确定后,标记错误等价于标记缺失.本文从极大似然估计角度,将标记作为待估量和轨道量一同考虑,采用EM方法给出了解决方案,实现了观测资料的区分与多个目标轨道同时改进,提高了资料的利用率.
2 问题的分析
2.1 轨道确定问题
简要回顾一下轨道确定(轨道改进)问题.令→Y为观测量,→X为轨道状态量,有测量方程

以及状态转移关系:

其中0为t0时刻的状态量.F、G为非线性函数.若t0时刻参考轨道为,上述方程可在处线性化为:
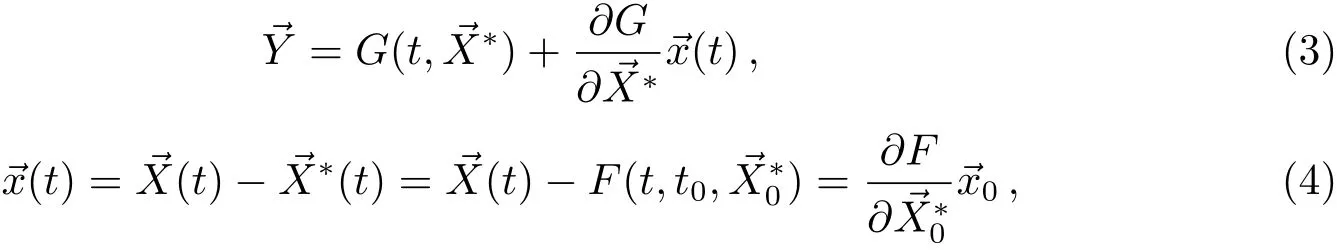
其中表示,即t0时刻真值和参考轨道的差.由上述两式可得到轨道改进的方程:
(5)式就是轨道改进的线性化方程,左边通常称为O−C.后续所有讨论都针对(5)式,在叙述中我们不再区分原始观测量和O−C量(统一称作观测量),以及状态量和状态改变量(统一称作状态量).
2.2 极大似然估计
对于本文讨论的多星定轨问题,令采集了属于n个目标的m圈观测资料,观测量为共m圈,表示第i圈资料;每圈又包含若干个资料其中pi是第i圈资料个数.状态量为其中表示第j个目标的状态量.定轨还需要知道资料和目标的对应关系,引入变量当Zij=1时,表示对应于目标.每圈必然并且仅属于一个目标,有:

轨道确定问题本质是最优估计问题,考虑极大似然估计,对数似然函数为:

其中p(·)表示概率密度函数,轨道改进即求:

假设

则
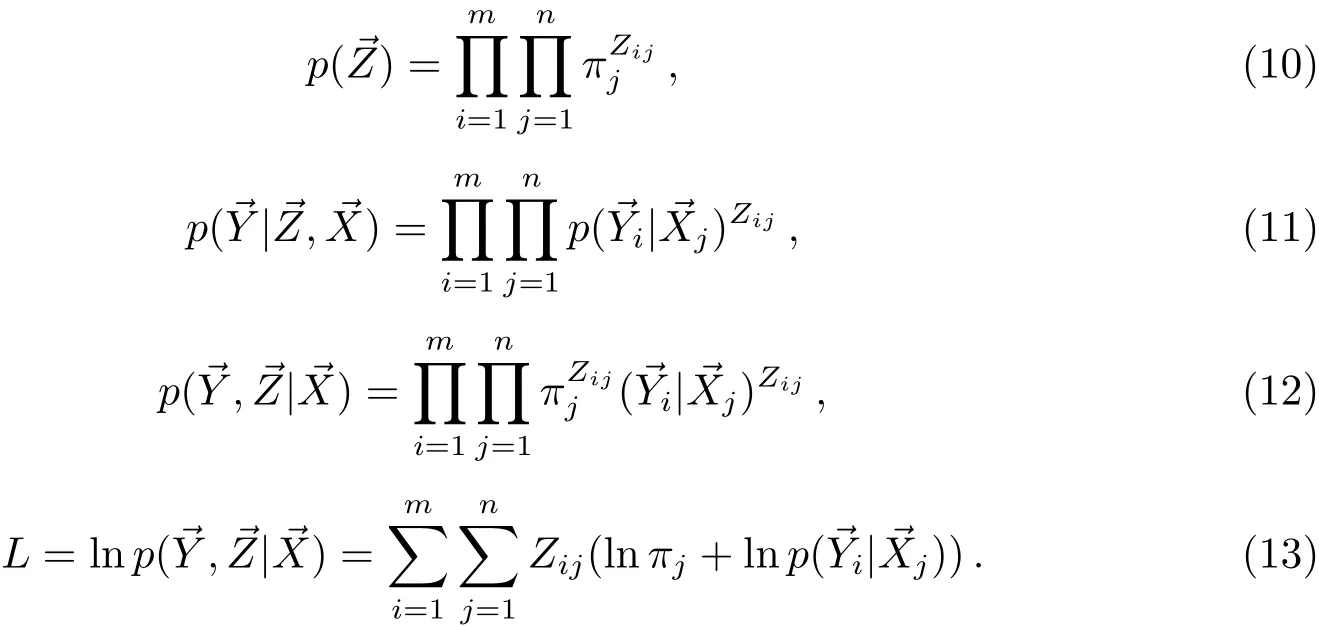
对于一般情形,和的对应关系Zij是已知的,可按照j将Zij=1的圈分为1组,即按照目标分为n组:
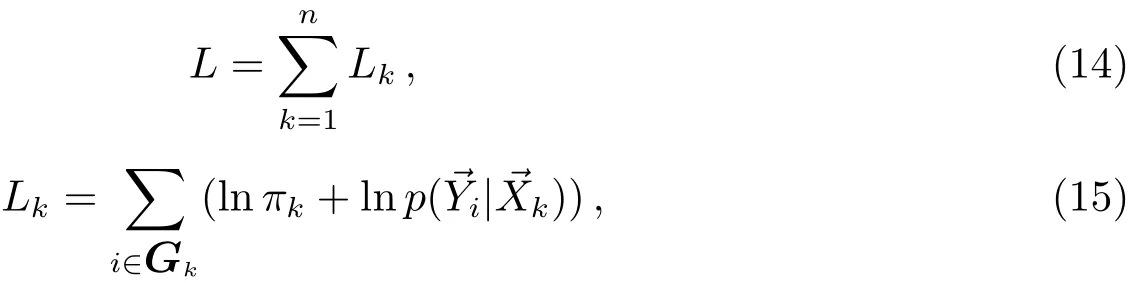
其中Gk={i,Zik=1}.由于各Lk之间无关,最大化L等价于最大化每个Lk.假设测量误差为正态分布:

其中是第i圈的测量误差:

则有:
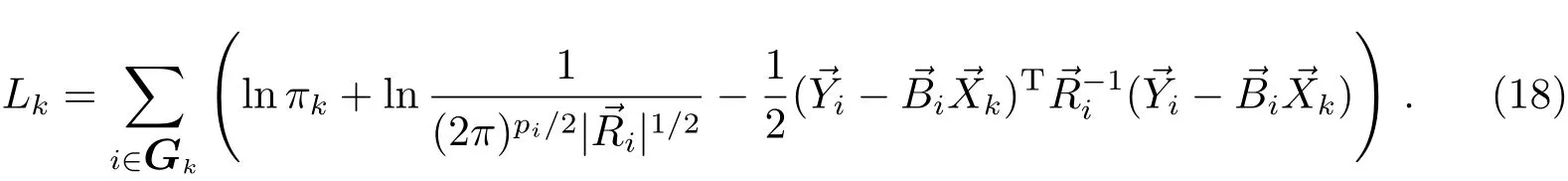
Lk最大时满足:
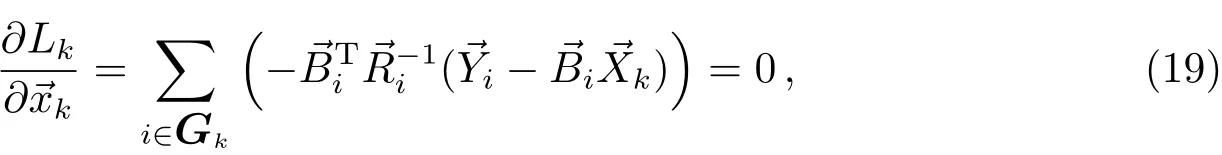
等价于逐个目标分别求解.(19)式的解也就是单目标定轨的极大似然估计[2].
若令:
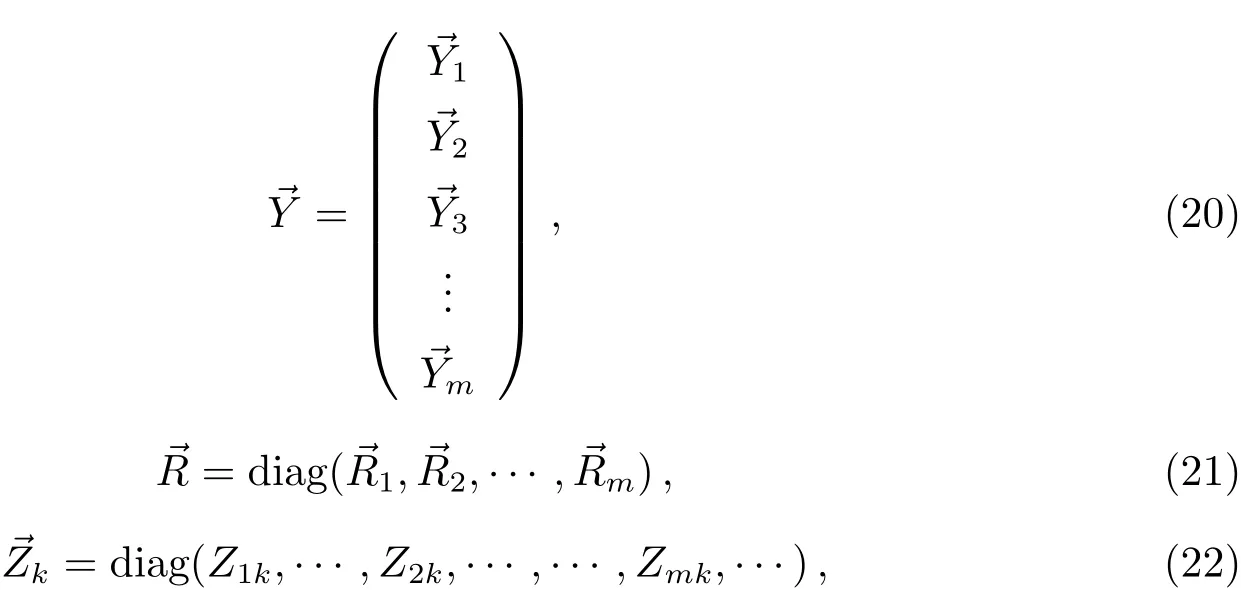
上式中···表示每个Zik值重复pi次.每个目标的解可写为统一形式:
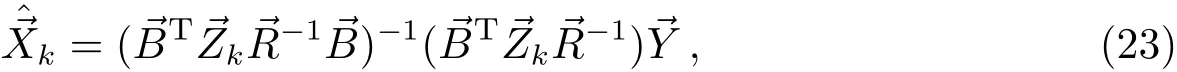
形式上和单目标轨道改进一样,只是增加了权重→Zk.
2.3 缺失变量模型与EM方法
对于本文讨论的多星混合资料定轨问题,由于标号是错误的,因此可看作是未知的,即缺失变量.假设的分布函数为q(),有:

多星混合资料定轨问题的似然函数为:

可分解为:
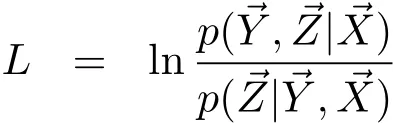
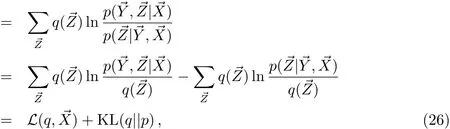
其中右边第2项KL(q||p)为Kullback-Leibler散度(KL divergence),其性质为KL(q||p)≥0,当且仅当时取等号.显然L为似然函数L的下界[3].
由于缺失变量的存在,直接求解(25)式的最大值是十分困难的,可通过EM方法求解[4].EM方法的求解思路是,由于L与无关,因此L最大时,KL(q||p)=0,等价于最大化L的下界L.而
EM方法为一迭代过程,每次迭代分为两个步骤:(1)期望步骤(E步骤,E Step):固定old,得到;(2)最大化步骤(M步骤,M Step),固定E步得到的q,在完整模型下求得new,此时由于发生了变化,因此KL(q||p)>0,将new作为old重新回到E步骤.迭代收敛时就得到了最大化L的.
3 问题的解决
根据上述思路,本文提出的问题得以解决.利用、估计,由此得到完整的观测量,化为多个一般定轨问题.由(10)~(11)式,根据Bayes公式可得:
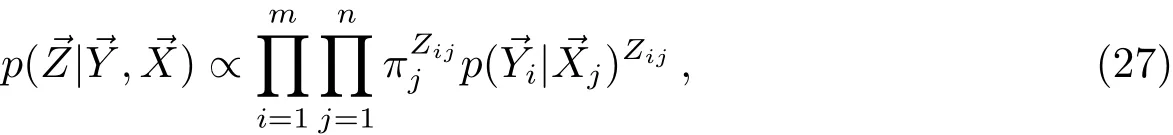
其中πj理解为第j个目标的先验概率,即获得的m圈资料中属于j目标的先验比例.由此可得到的数学期望.E步骤为:
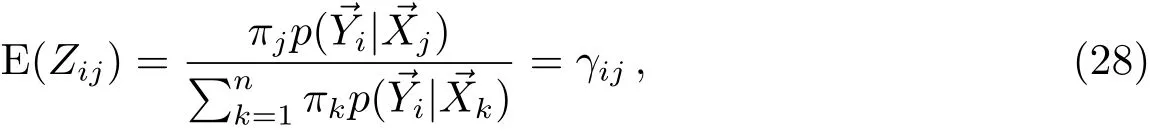
将γij作为Zij代入(13)式:
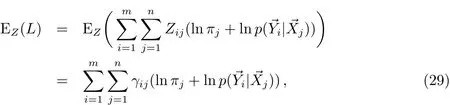
可见M步骤最大化的是似然函数相对于的数学期望.因此EM方法是最大化似然函数的期望.L依然按照下标j分组,最大化L依然等价于最大化每个Lk.将γij作为Zij代入(23)式可得到解.
多星混合资料定轨过程总结如下:(1)已知资料和精度矩阵以及观测所属目标的轨道初值;(2)由(28)式根据和计算;(3)根据,按照一般轨道改进过程,以1作为权矩阵,按目标逐一求得改进量判断改进量是否收敛,不收敛返回第2步.
4 稳健估计
上述虽然实现了多星混合资料定轨的完整过程,但在具体算法实现中还需要解决一个问题.上述过程中虽然Zij∈{0,1},但γij∈[0,1],由(23)式可见,对于某个目标的定轨中将会使用所有的资料,分别以γij为权重,在定轨的前几次迭代中,由于识别尚不完全准确,会出现同一圈资料以不同权重属于不同目标的情况,即0<γij<1,意味着对于某目标的轨道改进中会遇到大偏差的观测量.由于最小二乘估计是不稳健的,这将导致求解结果出现大偏差,从而影响后续识别过程,最终导致求解失败.因此在前几次迭代中必须使用稳健方法,来消除因识别尚不十分精确带来的影响.
文献[5-6]使用最小一乘估计用于初轨计算,指出最小一乘估计一方面具有很高的崩溃点,另一方面无需任何参数的设置,适用性比较好.这两个特点非常有利于上述问题的解决,而且识别精确后,对于本文问题可以转为最小二乘估计,从而弥补最小一乘估计在解唯一性以及渐近效率上的不足.文献[5-6]将最小一乘估计问题转换为线性规划问题求解.本文讨论的是轨道改进问题,已具有初始参考解,可采用迭代重加权方法(IRLS,Iteratively Reweighted Least Square)求解[7].对于定轨问题的最小二乘估计是:

最小一乘估计是:

IRLS方法也是一个迭代过程:
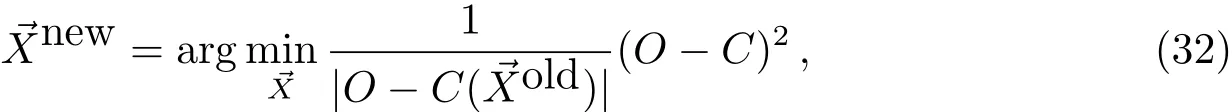
即以参考轨道计算的|O−C|−1作为权重,进行最小二乘估计,迭代收敛时

由于轨道改进本身就是迭代过程,因此无需每次迭代中都通过迭代严格求解最小一乘估计,轨道改进迭代过程中同时更新参考解和权重,因此应用IRLS方法只需在轨道改进过程中增加权重|O−C|−1即可.
5 数值模拟
采用数值模拟方法对上述方法进行了验证,选用的两个目标在历元时刻直角坐标系下的位置、速度见表1.两个目标位于相同轨道,平近点角差0.6°.

表1 模拟参考轨道Table 1 The reference orbits of simulation
模拟了3天2站6圈的观测数据,不同目标选用不同测站的观测,模拟数据类型为赤经和赤纬(α,δ).力模型包含90×90阶地球引力场、日月第三体摄动,太阳光压和大气阻力摄动.得到的资料情况如表2.两个目标相对同一个测站观测角距<2°.
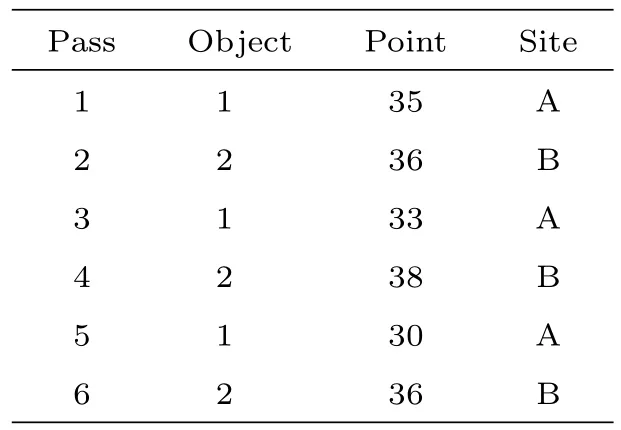
表2 模拟圈次情况Table 2 Description of simulated passes
为了验证程序的正确性,首先采用了和模拟完全一样的力模型,观测资料没有加误差.改进参数为目标的状态量,求解中前3次采用最小一乘估计.没有其它先验信息,取π1=π2=0.5.定轨中采用的初值见表3.

表3 定轨初值Table 3 The initial values of orbit determination
经过6次迭代后,两个目标的位置改进量都<1m,得到的对应关系与模拟一致.最终状态量见表4,与模拟采用的参考值一致,表明方法和程序的正确性.

表4 无误差资料的轨道改进结果Table 4 The results of orbit improvement with the observations without errors
为了仿真实际情况,定轨中将地球引力场在20×20阶处截断,大气阻力中系数CD由2.2变为2.3,作为模型误差.观测资料中增加了5′′的随机差,其它参数保持不变.定轨初值不变,对应关系求解正确,最终结果见表5.

表5 有误差资料的轨道改进结果Table 5 The results of orbit improvement with the observations with errors
在实际工作中,当根据标记目标处理数据失败时,是无法预先得知其中是否包含了多星,可能是只包含了编队中的另一个目标.因此模拟了一个目标的情况,仅保留目标2的3圈资料,采用同样的过程处理,依然选取π1=π2=0.5,结果见表6.目标2得到了正确的结果,最终识别结果为γ11=γ21=γ31=0,γ12=γ22=γ32=1,即所有3圈都属于目标2.目标1结果并不正确,是因为在第1次迭代的E步骤中由于初值误差,得到γ31=0.07,γ32=0.93.从而导致目标1在M步骤中定轨错误,第2次迭代开始已没有任何属于目标1的资料,轨道也不再修正.这个现象在实际计算中是容易判断的,并不会构成任何混淆.

表6 单目标轨道改进结果Table 6 The results of orbit improvement with the observations of single object
本文采用的稳健方法也可单独用于常规的轨道改进中,保留了3圈目标2和1圈目标1的观测资料(去除第1和第5圈资料)共142个资料,仅采用最小二乘估计,无法完成轨道改进.前3次按本文加权方法采用最小一乘估计后再使用最小二乘估计,并根据3倍残差进行资料剔除.最终正确剔除了属于目标1的33个资料,得到了正确的改进结果,见表7.

表7 稳健轨道改进结果Table 7 The results of robust orbit improvement
最后模拟了3星混合资料的情况,新增目标3的参考轨道和定轨初值见表8,目标3和目标2的观测角距最大约为2°.将目标3的2圈模拟资料和原先的6圈资料共同组成8圈3星混合资料,轨道改进中取π1=π2=π3=0.33,最终求解结果正确,见表9.

表8 目标3的模拟参数Table 8 The simulation parameters of the object 3

表9 3星轨道改进结果Table 9 The results of orbit improvement with the three objects
6 结论与讨论
本文针对光学观测日常定轨中的多星混合资料问题,给出了有效的处理方法.不同于现有方法,方法将资料标记和轨道量一同作为待估量,并融合了识别和定轨过程,识别不仅依赖初值,在轨道改进过程中随着轨道修正不断动态调整.在轨道改进中,采用IRLS方法实现最小一乘稳健估计,不改变原有迭代计算过程,权重选取也无需调整参数,应用有效、简便.
本文没有采用逐点识别,是考虑到现有跟踪系统都通过航迹关联实现闭环跟踪.同一圈资料一般属于同一个目标,按圈设置Zij更为合理.对于单点采集资料,例如搜索或巡天观测方式,本文方法同样适用,只需将每圈观测看作只有一个采样即可.
[1]吴连大.人造卫星和空间碎片的轨道和探测.北京:中国科学技术出版社,2011:250-253
[2]Tapley B D,Schuts B E,Born G R.Statistical Orbit Determination.Amsterdam:Elsevier Academic Press,2004:190-194
[3]Bishop C M.Pattern Recognition and Machine Learning.New York:Springer,2006:430-443
[4]Dempster A P,Laird N M,Rubin D B.Journal of the Royal Statistical Society.Series B(Methodological),1977,39:1
[5]王歆.天文学报,2013,54:274
[6]Wang X.ChA&A,2013,37:455
[7]Scales J A,Gersztenkorn A.InvPr,1988,4:1071
Orbit Determination with Mixture Observations of Multiple Objects
WANG Xin1,2
(1 Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008)(2 Key Laboratory of Space Object and Debris Observation,Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008)
In the operational orbit determination with optical measurements of space objects,some observations of different objects are tagged as the same object.For this kind of data,the orbit improvement according to the tag is failed because of the composition of multiple objects.A method is proposed from the view of maximum likelihood,and it combines the orbit improvement and identi fication by employing the EM(Expectation Maximum)method.In the implementation of this method,a robust estimation is also given.Corresponding numerical simulations show that the method is feasible,effective,and convenient.
space vehicles,celestial mechanics,methods:statistical
P135;
A
2014-05-04收到原稿,2014-06-10收到修改稿
∗国家自然科学基金项目(11373072)资助
†wangxin@pmo.ac.cn
