脉冲星射电辐射束半径与周期关系的研究∗
2014-11-29魏丁丁游霄鹏
魏丁丁 游霄鹏
(西南大学物理科学与技术学院重庆400715)
脉冲星射电辐射束半径与周期关系的研究∗
魏丁丁 游霄鹏†
(西南大学物理科学与技术学院重庆400715)
脉冲星的周期非常稳定.前人通过研究发现脉冲星射电辐射束半径大小应该正比于周期的−1/3或−1/2次方.通过整理收集了87颗信噪比很好的、偏振位置角明显为“S”曲线的脉冲星数据,用脉冲星辐射束几何模型计算得到了每颗脉冲星的辐射束半径及误差.发现脉冲星周期小于0.85 s时,辐射束半径正比于周期的−1/2次方.周期大于0.85 s时,辐射束半径与周期之间并没有明显的幂律关系,但这可能与选择效应有关.当假设脉冲星的磁倾角为90°时,计算得到的辐射束半径随周期分布的下边界正比于周期的−1/2次方,与前人的结论一致.
脉冲星:普通,方法:统计
1 引言
脉冲星具有很强的磁场,是高速自转的磁中子星,其自转周期P很稳定.脉冲星的辐射一般用灯塔模型来解释.当脉冲星每自转1周,其辐射束若扫过观测者视线,就能观测到脉冲信号.单个脉冲信号的轮廓变化很大,但多个脉冲信号的累积轮廓非常稳定.一般呈现出单峰、双峰、三峰以及多峰等形态[1],可用经验的核锥模型[2]或补丁模型[3]来解释.最近,还提出了辐射束的风扇模型[4].前人研究了核锥模型中核成分与锥成分的宽度关系[5−7].
脉冲星的辐射束模型最早由Radhakrishnan等[8]提出,其几何形状如图1所示.图中3条轴线分别代表脉冲星的自转轴、磁轴和观测者的视线方向.自转轴与磁轴之间的夹角是磁倾角α.当辐射束绕自转轴旋转时,磁轴与视线距离最近时所张的角度为撞击角β.图中ψ是偏振位置角,而ϕ为辐射轮廓的相位.根据此模型,ψ随ϕ的变化应该呈“S”曲线.辐射束半径大小为ρ,图中ST曲线在赤道圈上的投影对球心的张角值为辐射轮廓的宽度W.
脉冲星辐射束半径ρ可以通过脉冲宽度W以及磁倾角α、撞击角β计算得到.前人研究了辐射束半径与脉冲星自转周期P的关系.Lyne等[3]取α为90°,得出ρ的下限值正比于周期的−1/3次方,并且通过分析说明辐射束更像是补丁模型.Rankin[2,9]基于核锥模型研究得出了在1 GHz附近,核成分与锥成分的角半径的下限值都正比于周期的−1/2次方.最近,Maciesiak等[10−12]用具有中间脉冲的脉冲星进行分析,同样得出了核成分与锥成分的角半径下限值都正比于周期的−1/2次方.
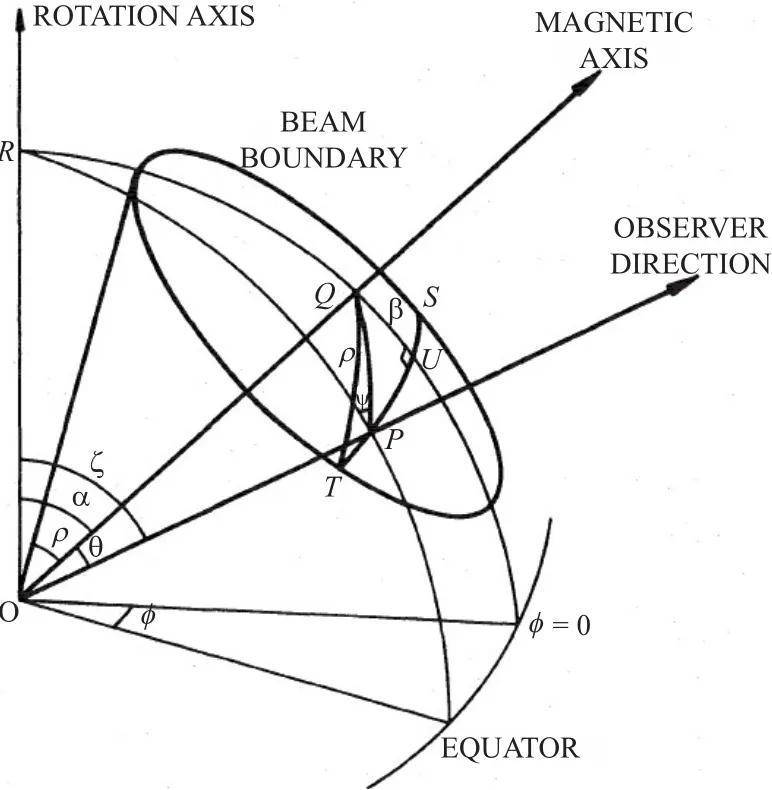
图1 脉冲星辐射束的几何模型.图形来自Lyne等[3]Fig.1 The geometry of the radiation beam model for pulsars taken from Lyne et al[3]
前人的工作得出的结论主要是辐射束半径的下限值与周期的关系,依赖于α接近于90°,而且轮廓宽度值的测量方式也有不同,并且他们的工作没有给出具体的脉冲星轮廓选择标准.因此本文将用更多的严格标准选择的脉冲星偏振轮廓来重新分析数据,并且希望得出不依赖于α取值的辐射束半径与周期之间的关系.
2 数据的收集与处理
本文收集的数据主要来自欧洲脉冲星多频轮廓数据库(EPN),其中包含了1 000多颗脉冲星的多种频段的偏振数据.偏振数据中包含了脉冲星的相位ϕ,斯托克斯参量I、Q、U、V的信息.我们从中严格挑选出了87颗很好的脉冲星数据[13−17],选择标准如下:(1)具有偏振轮廓;(2)轮廓的信噪比高,若为多频观测,则选择其中信噪比最好的频率的轮廓图;(3)偏振位置角曲线呈现比较明显的“S”型.我们对选取的每一颗脉冲星作了偏振轮廓图.图2展示了其中的6颗.每个脉冲星轮廓图的上部分为偏振流量轮廓图,其中实线代表总流量I,点线代表线偏振强度虚线代表圆偏振强度V.中间部分为偏振位置角ψ随相位ϕ的变化,ψ=1/2tan−1(U/Q),偏振位置角的误差由误差传递公式计算得出,其中σU和σQ是用U和Q在脉冲轮廓外的噪音值计算得到.偏振位置角曲线有时会出现180°的跃变,或由于正交模式的影响[18]出现90°的跃变,我们对此跃变作了修正后,由图2下半部分给出,并计算出dψ/dϕ的最大值,用直线画出.
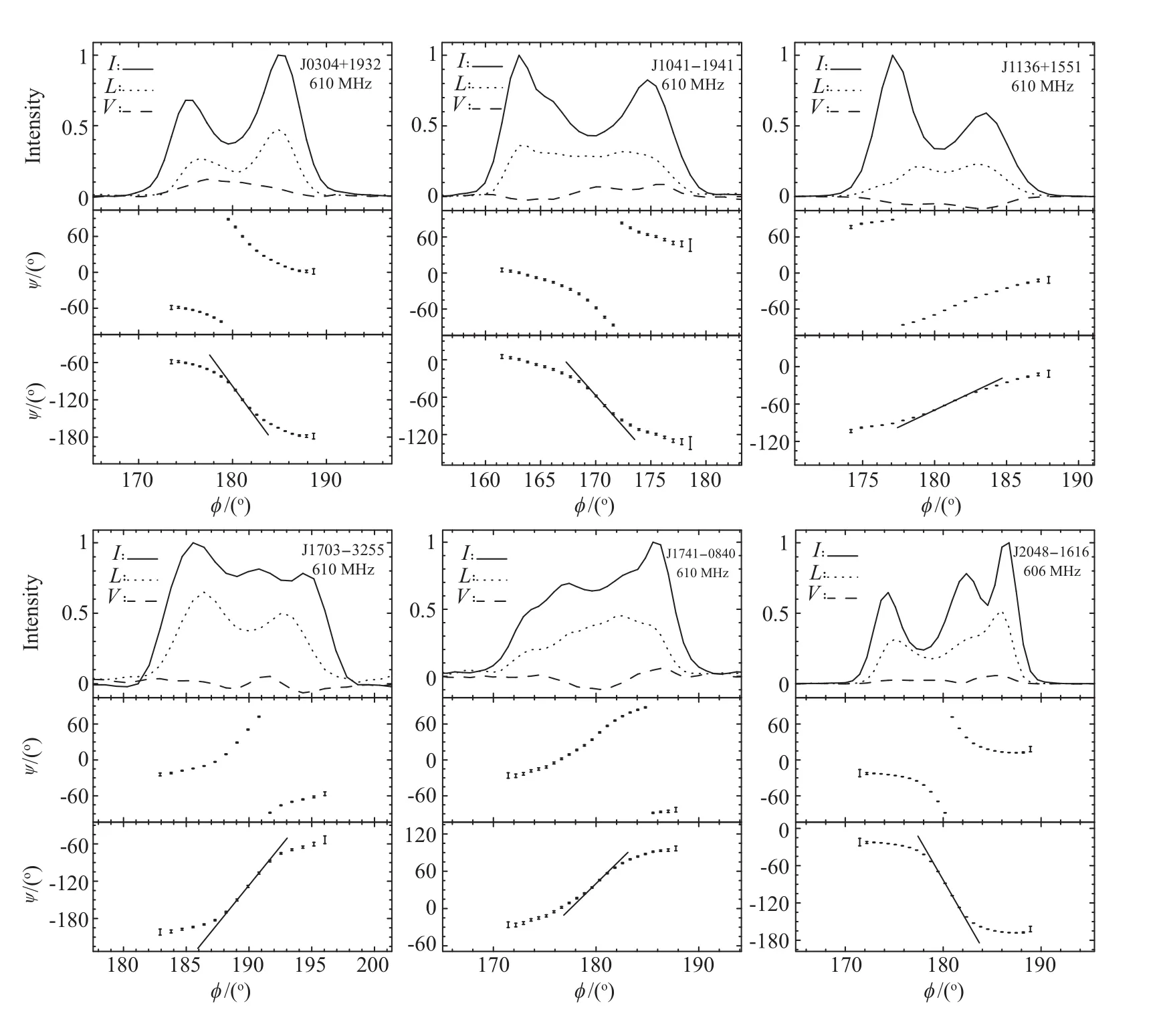
图2 6个脉冲星的偏振轮廓及偏振位置角曲线图.其中每个脉冲星图的上半部分为偏振轮廓曲线,实线为总流量,点线为线偏振,虚线为圆偏振.中间部分为偏振位置角曲线图.下半部分为进行180°或90°跃变修正后的偏振位置角曲线图,直线为dψ/dϕ的最大值.Fig.2 Polarization and position angle profiles for 6 pulsars.For each pulsar,the upper panel shows the polarization profiles.The solid,dotted,and dashed lines represent the total intensity,the linear and circular polarization,respectively.The middle panel shows the position angle curves.The lower panel shows the position angle curves after the correction for 180° or 90° jumping,and the straight line represents dψ/dϕ|max.
我们能从偏振轮廓图得到轮廓的宽度,而脉冲宽度W的测量也有多种方式.一般情况下,W10为轮廓峰值取10%后轮廓所对应的宽度,W50是峰值取50%后所对应的宽度.若为双峰以上型轮廓,则取距离最远的两个峰之间的宽度为峰峰宽Wpp.对于脉冲轮廓为单峰的情况,脉冲宽度就只有W10和W50两个值.表1列出了筛选出的87颗脉冲星的参数,第1列是脉冲星的名字,第2列为脉冲星的观测频率,第3列为周期,第4列为参考文献,第5列至第7列分别为W10、W50和Wpp,第8列为偏振位置角曲线斜率最大值.
由图1所示的辐射束几何图可知,辐射束半径ρ与磁倾角α、撞击角β、轮廓宽度W之间的几何关系为[3]
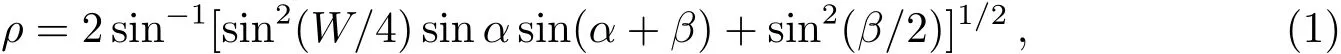
而偏振位置角曲线的斜率的最大值为

由偏振位置角曲线斜率的最大值公式,如果知道α的值,就由(2)式可得β值.再根据(1)式,测量出轮廓的宽度W,就能得出辐射束半径ρ.考虑目前文献中通过不同方法给出的α值通常有很大的不确定度,且样本较少.为了使结果不依赖于α的取值,我们设定α的值分别为90°、60°、45°和30°.再根据脉冲星轮廓的形状,采用3个(多峰)或两个(单峰)宽度值,这样每颗脉冲星就可以求得12或8个脉冲星辐射束半径的值.我们把这12或8个值取平均作为脉冲星辐射束半径的值,均方根作为误差,就可以检验脉冲星辐射束半径与周期之间的关系.
3 结果和分析
图3给出了87颗脉冲星辐射束半径的分布图.从图中可以看出脉冲星辐射束半径的值大部分分布在10°以下,在我们的样本中占了83%,说明脉冲星的辐射束一般较窄.但也有例外.如PSR J1932+1059的ρ达到了32°.该脉冲星的dψ/dϕ|max值很小,说明β值较大,视线比较靠近辐射束的外围.
图4给出了87颗脉冲星的辐射束半径ρ随周期P变化的关系图.很容易看出在周期小于0.85 s时(图4点线以左),ρ明显有随P增大而减小的趋势.但P大于0.85 s时,这一变化不明显.因此我们首先分析P小于0.85 s的脉冲星,共有49颗,如图5所示.我们用加权最小二乘法拟合ρ=cPb,得出c=3.00°±0.47°,b=−0.47±0.17,接近于Rankin[9]得出的ρ=2.45°P−0.5的关系,如图5中的实线所示.如果固定b的值分别为−0.5和−0.33进行拟合,得出结果如图5中的点划线和虚线所示.可以看出我们的拟合结果非常接近于ρ∝P−0.5,而离ρ∝P−0.33的线较远.
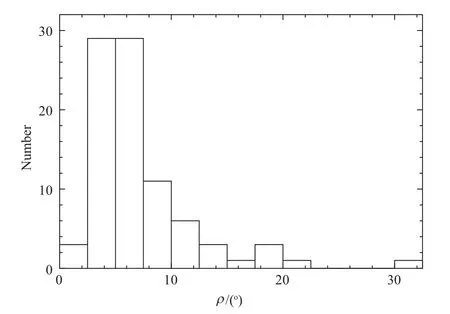
图3 脉冲星辐射束半径分布图Fig.3 The distribution histogram of the pulsar radiation beam radii
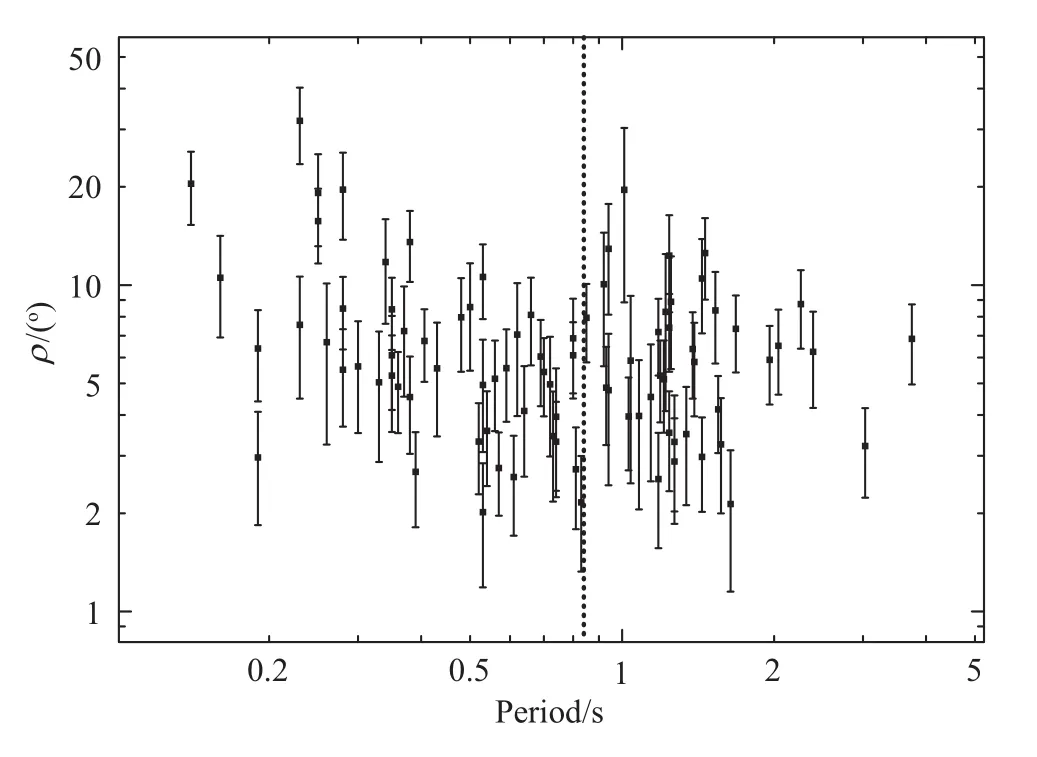
图4 87颗脉冲星的辐射束半径与周期关系图.其中点线表示P=0.85 s的分界线.Fig.4 The relation between pulsar beam radii and periods for 87 pulsars.The dotted line represents P=0.85 s.
对于P大于0.85 s的脉冲星,共38颗,我们做了类似的拟合,结果如图6所示.实线为拟合出的b=−0.02±0.25,接近于0,说明ρ与P的关系确实并不明显,而且与b=−0.5和b=−0.33的点划线与虚线都相差很远.因此当P大于0.85 s时,我们的样本显示ρ与P不成幂律关系.但这可能与选择效应有关.如果满足ρ∝P−0.5的关系,则P越大,要求ρ越小,则观测到脉冲星的概率就较小.按照前面所述的选择标准,我们选择的较长周期的脉冲星可能ρ会相对偏大,造成不满足ρ∝P−0.5的关系.而且为了保证信噪比和偏振位置角的形状,我们选择的轮廓的观测频率并不相同,而有些脉冲星的轮廓宽度会随着频率有明显的变化,这样会导致宽度的弥散,这也有可能影响统计结果.
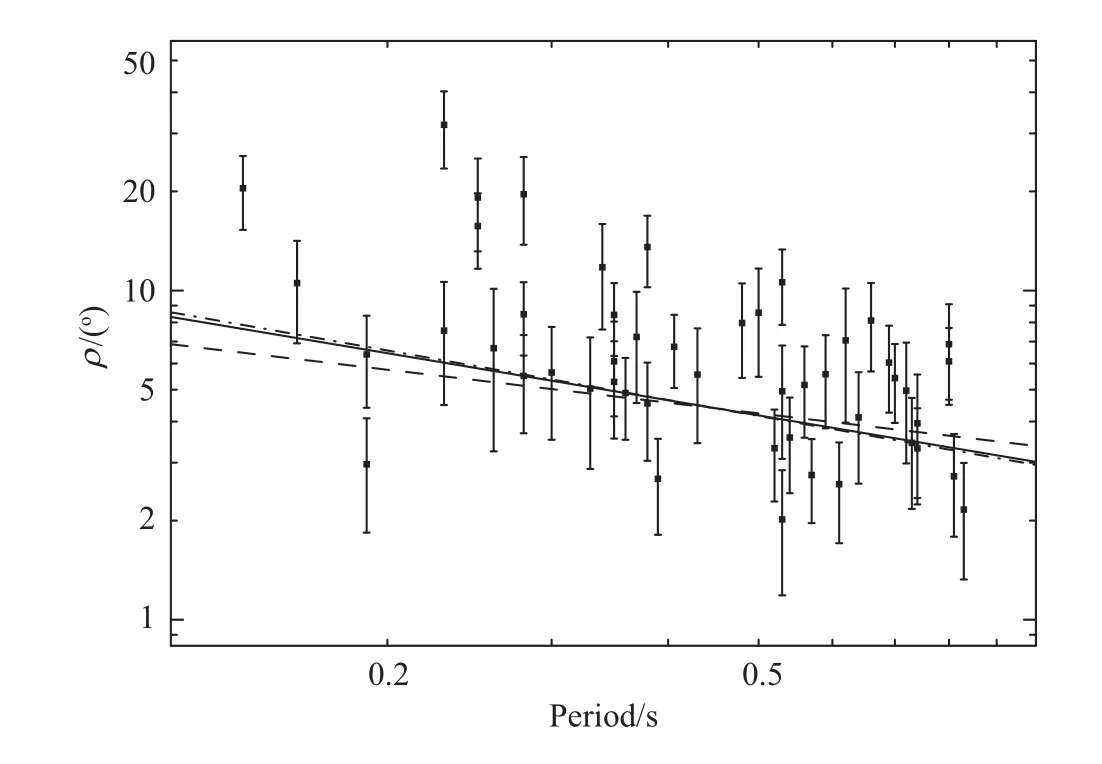
图5 49颗P<0.85 s脉冲星的辐射束半径与周期关系图.实线表示ρ=3.00°P−0.47,点划线为ρ=2.94°P−0.5,虚线为ρ =3.36°P−0.33.Fig.5 The relation between pulsar beam radii and periods for 49 pulsars with P<0.85 s.The solid,dot-dashed,and dashed lines represent ρ =3.00°P−0.47,ρ =2.94°P−0.5,and ρ =3.36°P−0.33,respectively.

图6 38颗P>0.85 s脉冲星的辐射束半径与周期关系图.实线表示ρ=4.45°P−0.02,点划线为ρ=5.17°P−0.5,虚线为ρ =4.94°P−0.33.Fig.6 The relation between pulsar beam radii and periods for 38 pulsars with P>0.85 s.The solid,dot-dashed,and dashed lines represent ρ =4.45°P−0.02,ρ =5.17°P−0.5,and ρ =4.94°P−0.33,respectively.
为了与前人工作中所取ρ的下限值的结果比较,我们计算了当α=90°和轮廓宽度为W10时的辐射束半径值ρ90.图7显示了ρ90与P的关系.Rankin[9]提出ρ=2.45°P−0.5/sinα,若α=90°,则公式简化为ρ90=2.45°P−0.5. 图7中的实线为ρ90=2.45°P−0.5,可以看出我们的结果与该下限关系符合得非常好.
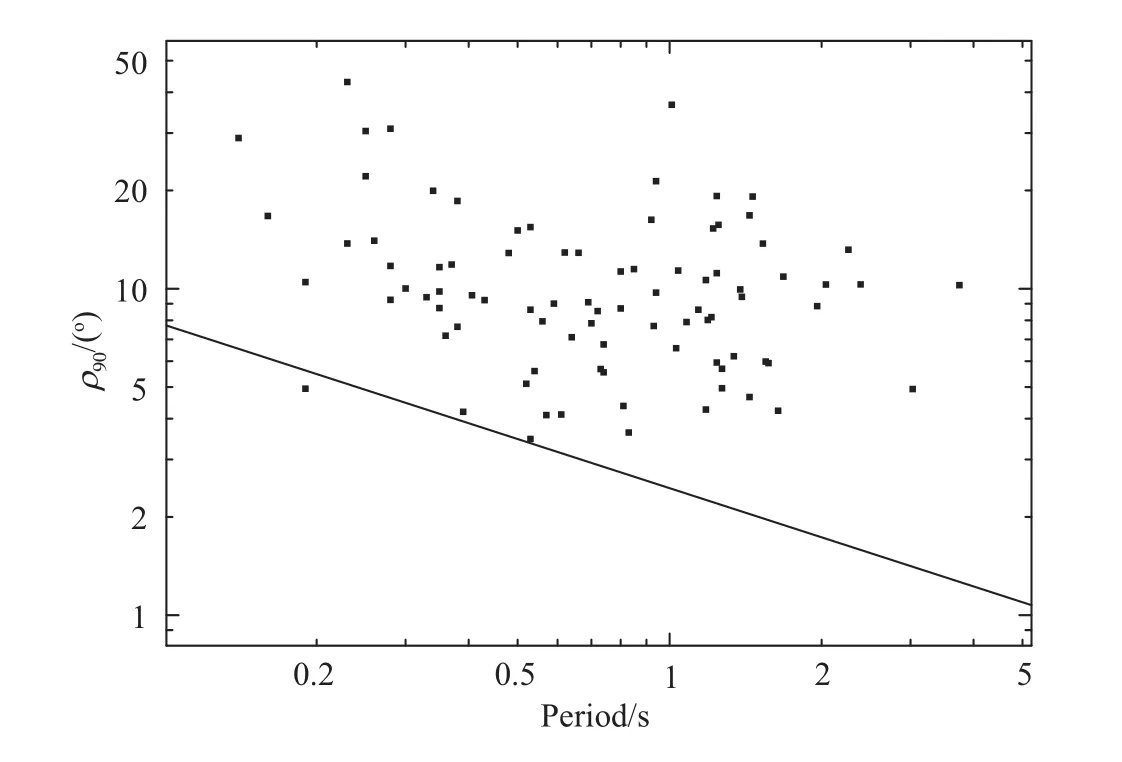
图7 脉冲星辐射束半径下限值与周期关系图.实线为ρ90=2.45°P−0.5.Fig.7 The relation between the lower boundary of pulsar radiation beam radii and periods.The solid line represents ρ90=2.45°P−0.5.
4 总结
我们利用在欧洲脉冲星多频轮廓数据库网站已经公开的数据,筛选了87颗信噪比较好、偏振位置曲线较明显为“S”型的脉冲星进行了研究.对每颗脉冲星都作了偏振位置角曲线,找出最大斜率值.为了验证不依赖于磁倾角的辐射束半径值ρ与周期P之间的关系,我们假设脉冲星的磁倾角α的值为90°、60°、45°和30°,取W10、W50和Wpp(多峰轮廓)或W10和W50(单峰轮廓)作为宽度值,求出了脉冲星辐射束半径值及误差,并用最小二乘法进行拟合.发现在我们的样本中,周期小于0.85 s的脉冲星符合ρ正比于P的−1/2次方的关系,大于0.85 s的脉冲星ρ未随P的增大而明显减小,但这在一定程度上受到选择效应的影响.若只取α的值为90°,我们求得的辐射束半径随周期分布的下边界符合Rankin[9]提出的ρ90=2.45°P−0.5的下限关系.
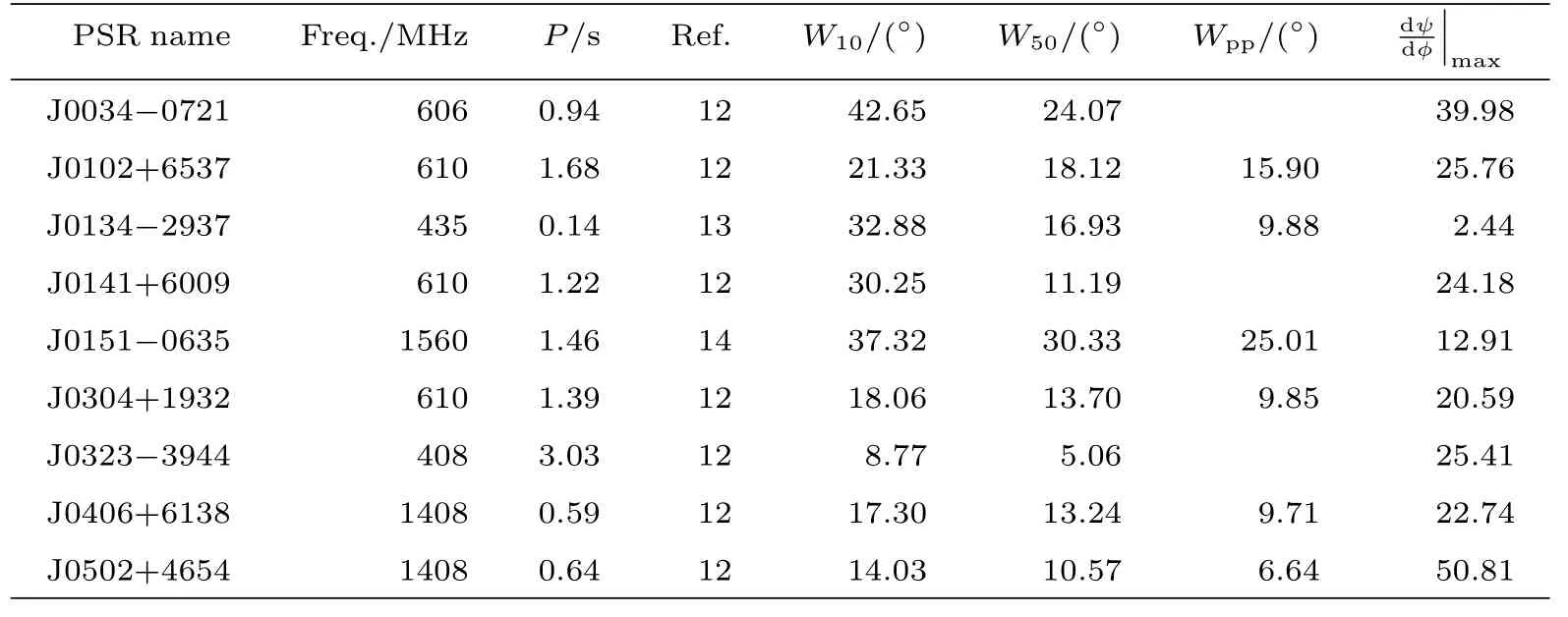
表1 87颗脉冲星的相关参数值Table 1 Parameters for 87 pulsars
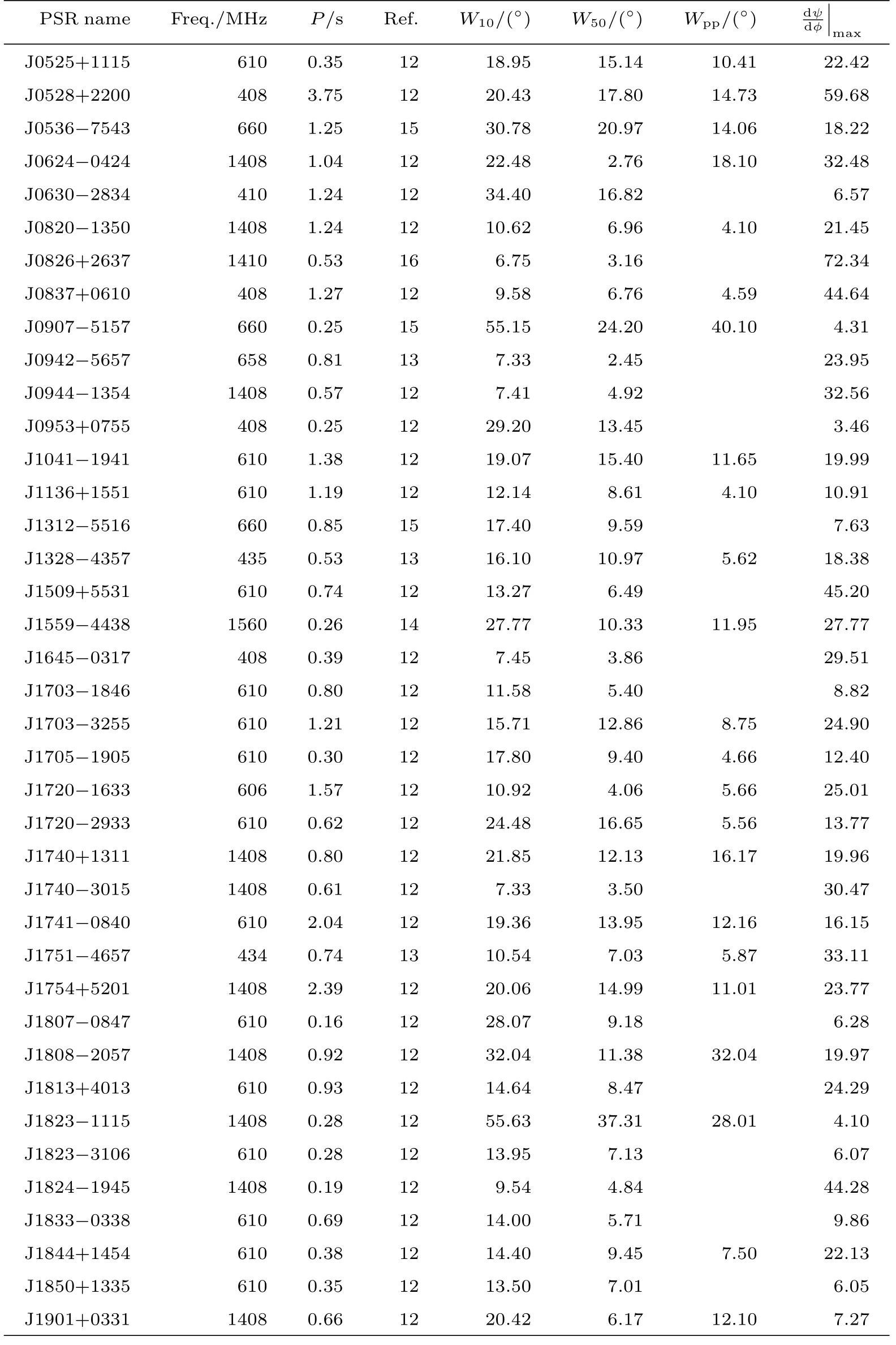
表1 续1Table 1 Continued 1
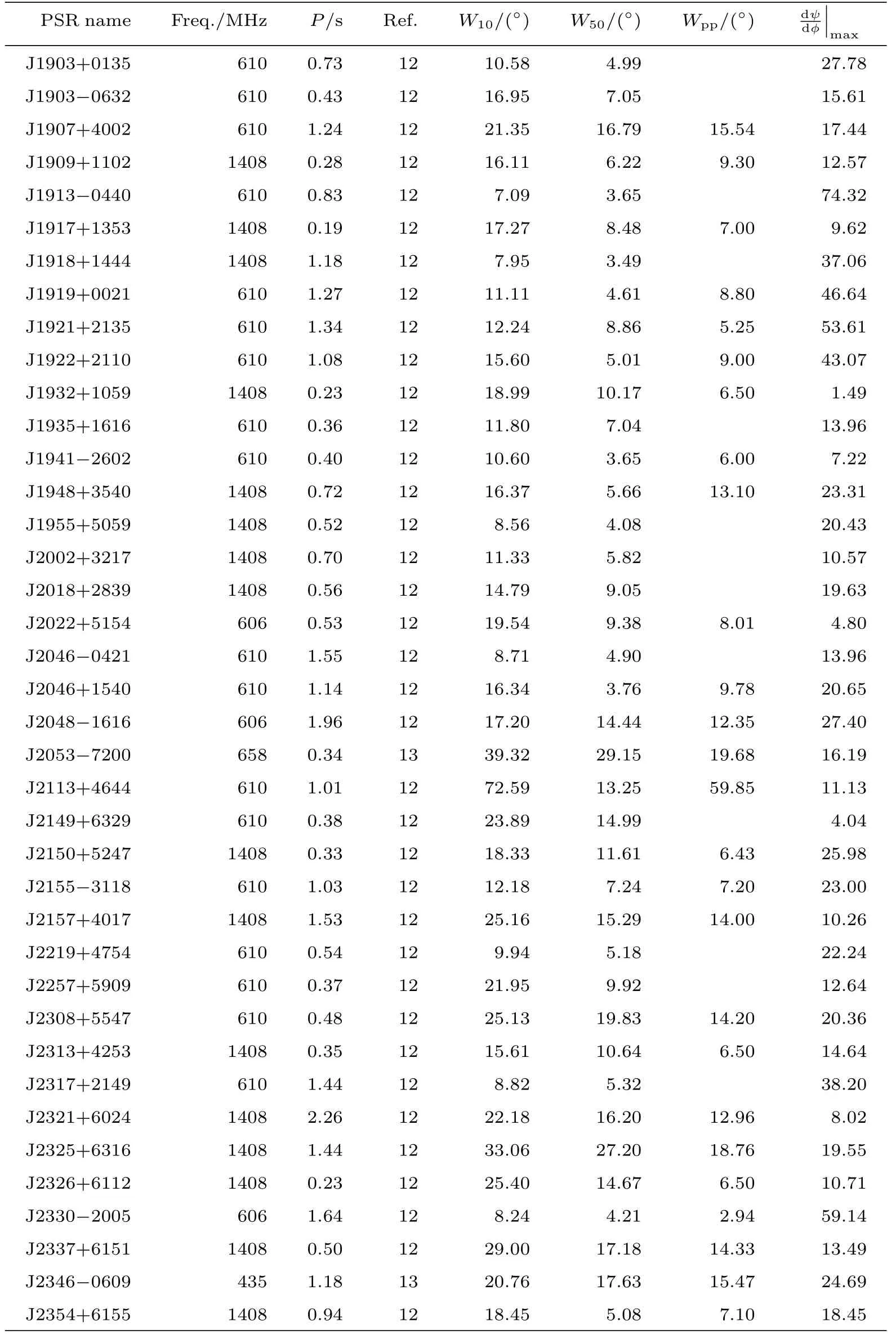
表1 续2Table 1 Continued 2
[1]Rankin J M.ApJ,1983,274:333
[2]Rankin J M.ApJ,1993,405:285
[3]Lyne A G,Manchester R N.MNRAS,1988,234:477
[4]Wang H G,Pi F P,Zheng X P,et al.arXiv:1405.6825
[5]Gould D M.Structure and Polarization of Pulsar Radio Emission Beams.Manchester:Univ.Manchester,1994:120
[6]蒋雪,游霄鹏.天文学报,2013,54:93
[7]Jiang X,You X P.ChA&A,2014,38:32
[8]Radhakrishnan V,Cooke D J.ApL,1969,3:225
[9]Rankin J M.ApJ,1990,352:247
[10]Maciesiak K,Gil J,Ribeiro V A R M.MNRAS,2011,414:1314
[11]Maciesiak K,Gil J.MNRAS,2011,417:1444
[12]Maciesiak K,Gil J,Melikidze G.MNRAS,2012,424:1762
[13]Gould D M,Lyne A G.MNRAS,1998,301:235
[14]Manchester R N,Han J L,Qiao G J.MNRAS,1998,295:280
[15]Wu X J,Manchester R N,Lyne A G,et al.MNRAS,1993,261:630
[16]Qiao G J,Manchester R N,Lyne A G,et al.MNRAS,1995,274:572
[17]von Hoensbroech A,Xilouris K M.A&AS,1997,324:981
[18]Cordes J M,Rankin J M,Backer D C.ApJ,1978,223:961
A Study on the Relation between Radio Radiation Beam Radii and Periods of Pulsars
WEI Ding-ding YOU Xiao-peng
(School of Physical Science and Technology,Southwest University,Chongqing 400715)
The period of pulsar is very stable.Some previous works have found that the pulsar radio radiation beam radius is proportional to the period with a power law index of−1/2 or−1/3.In this paper,87 pulsars with high signal-noise-ratio and obvious S shape curves of position angle are selected.The radius and error of radiation beam are calculated for each pulsar.We found that the distribution of pulsar beam radii is proportional to the periods with a power law index of−1/2 when the periods are smaller than 0.85 s.When periods are greater than 0.85 s,there is no signi ficant relation between pulsar beam radii and periods,but this is probably because of selection effect.When the inclination angle is assumed to be 90°,the lower boundary of beam radii is found to be proportional to the periods with a power law index of−1/2,which is consistent with the conclusions of previous works.
pulsars:general,methods:statistical
P145;
A
2014-06-03收到原稿,2014-06-16收到修改稿
∗国家自然科学天文联合基金项目(U1231120)资助
†yxp0910@swu.edu.cn
