引入制动管路约束的车辆操纵稳定性控制方法研究

王宪彬，邓红星，徐伟

（东北林业大学 交通学院，黑龙江哈尔滨150040）

目前车辆操纵稳定性动力学控制策略，多是以经典的二自由度模型为基础的车轮纵向力分配控制方法，主要以分层控制当中的期望直接横摆力矩[1－3]控制为基础，进行再分配[4]。如One[5]等人用最小的轮胎与路面附着极限来实现在4个驱动轮的地面切向反作用力的大小，以便使汽车运动稳定。李道飞和喻凡[6]采用基于符号保持二次规划法的控制分配算法来实现轮胎力的最优分配。邹永才[7]等人结合HSRI轮胎模型设计了降低整车路面附着负荷的目标函数，建立全轮纵向力优化分配模式，并通过约束优化得出全轮纵向力分配值。刘力[8]等人针对现有汽车稳定性控制系统中，汽车全轮纵向力分配算法在极端工况下出现轮胎力饱和，导致滑移率控制器过多介入而出现控制振荡和对控制目标的调整不合理等问题，提出了一种新的主动动态目标调整的全轮纵向力分配算法。但这些方法都没有考虑制动管路摩擦力的约束对各车轮纵向力分配的影响。大部分以车辆防抱制动系统（Anti-lock Brake System，ABS）为基础的全轮纵向力分配方法在建模过程中没有考虑到液压管路的影响，如郭孔辉等人在稳态特性仿真研究中，认为制动管路中制动液流量较小、液压管路内壁比较光滑，可以忽略管路的沿程压力损失和局部压力损失[9]。但在实际动态测试中，这种假设使仿真结果和实际结论存在较大差别。也就是说如果在建模中引入制动管路摩擦力特性，将使得期望横摆力矩的分布特征可能将发生较大变化。

目前管路摩擦力模型通常是以线性摩擦力为基础的。而由于液压传动介质的流动性、可压缩性、粘性、易受污染等特性以及易受温度、压力等环境的影响等原因，车辆制动管路中的摩擦力在实际中表现出很强的非线性，目前使用的模型难以解释摩擦力对汽车制动性能的影响。

综上所述，虽然车辆防抱制动系统（ABS）已经得到了普及的工程应用，但对考虑制动管路非线性摩擦力的全轮纵向力分配研究仍缺乏相应的理论基础。所以本文中笔者以直接横摆力矩控制（Direct Yaw-moment Control，DYC）为基础，结合车辆动力学模型和制动管路摩擦力模型的约束条件，在传统纵向力分配方法的基础上，建立引入制动管路约束的全轮纵向力优化分配算法，并用MATLAB软件进行仿真试验验证。

1 车辆系统动力学模型

本文中综合研究重点建立了3个自由度的汽车系统动力学模型（汽车的横向、纵向和横摆，并计算4个车轮的转动）。车辆模型如图1所示。

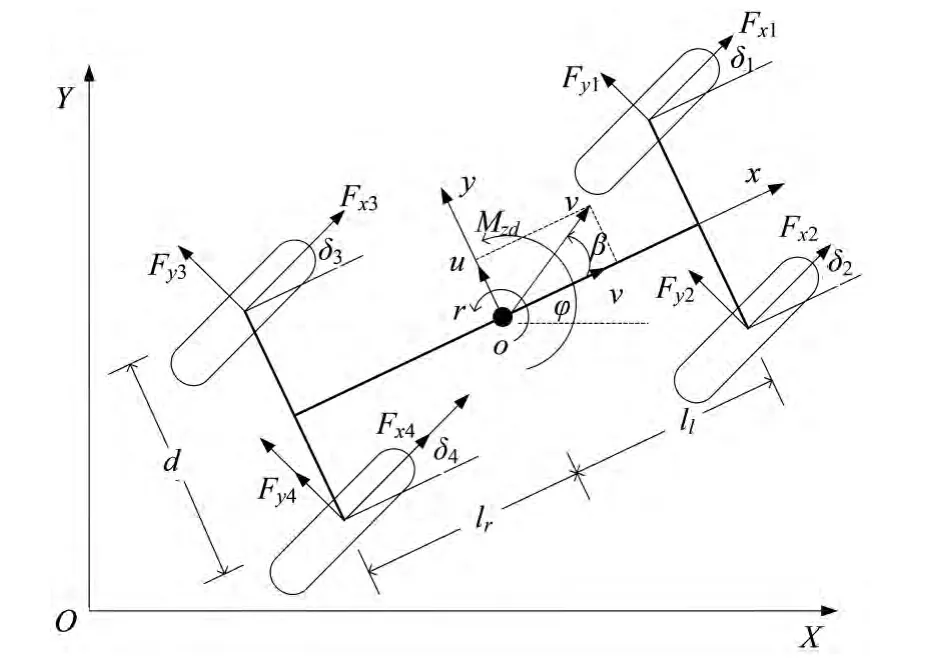
图1汽车模型

对整车模型进行了力学分析，在纵向上列出平衡方程：

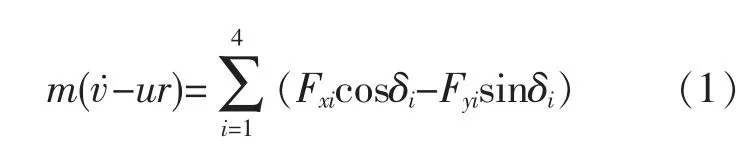
侧向上的平衡方程：

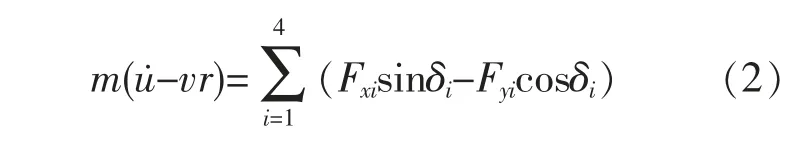
绕z轴的平衡方程：

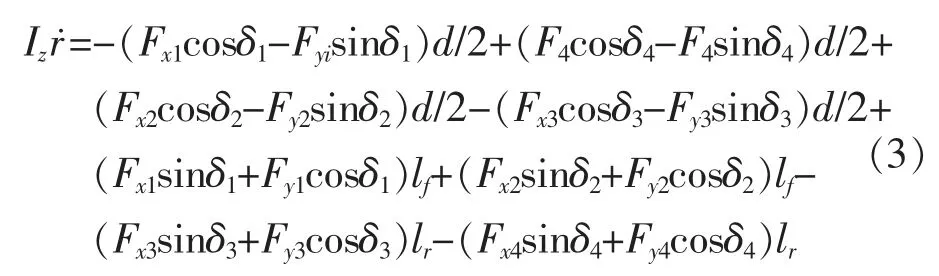
式中：r为车辆的横摆角速度；l为汽车轴距；lf为质心到前轴的距离；lr为质心到后轴的距离；φ为车辆的横摆角；v为x方向上车辆质心的速度；u为y方向上车辆质心的速度；m为车辆的总质量；Iz为整车绕车辆坐标系z轴的转动惯量；d为轮距；Fxi（i＝1，2，3，4）为车轮的纵向作用力；Fyi（i＝1，2，3，4）为车轮的侧向作用力。

2 制动系统建模

2.1 制动轮缸模型

在制动过程中，轮缸的压力等于主缸与节流阀之间以及节流阀与制动轮缸之间所有直管沿程压力损失、局部压力损失以及节流阀口前后之间的压力差三者的叠加[10]。因此，制动轮缸的压力，即距离主缸 ll的管路中压力可以表示为式（4）[11]：

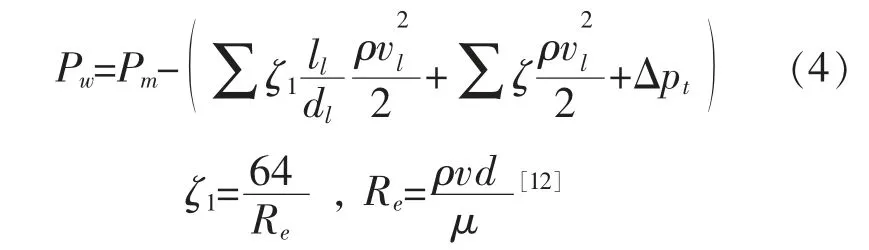
式中：Pm为制动主缸压力；ζ1为沿程阻力系数；ll为制动管长度；dl为制动管直径；ρ为制动液的密度；vl为制动液的平均流速；μ为液体粘度；ζ为局部阻力系数。

节流阀口前后压力差ΔPt可以表示为

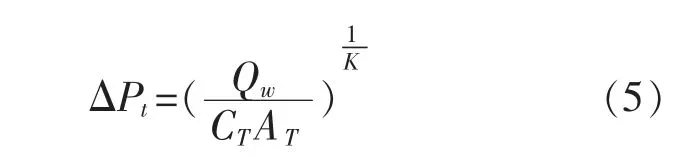
式中：Qw为轮缸的流量；CT为由节流阀口形状、制动液性质等因素决定的系数；AT为节流阀口的通流截面积；K为由阀口形状决定的节流阀指数。

制动液平均流速vl是流入轮缸的制动液流量Qw的函数。根据流体力学理论，规定制动轮缸流量的流入方向为正，考虑到制动器刚度的影响，则轮缸的连续流量方程为[10]

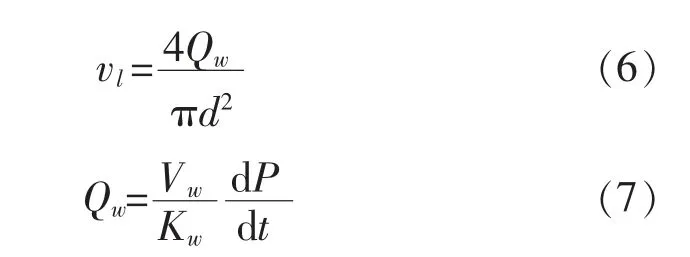
式中：Vw为制动轮缸容积；Kw为轮缸的等效体积弹性模量。

2.2 制动轮模型

对盘式制动器而言，施加在摩擦衬片上的单侧夹持力Fc可通过制动轮缸制动液的压力计算：

式中：Aw为制动轮缸活塞的面积。

如果制动器摩擦片与制动盘接触良好且制动盘上受力均匀，则制动器产生的摩擦力矩为

式中：f为摩擦系数；rs为制动器摩擦片的有效半径。在实际使用过程中，摩擦片是扇形的，如果扇形的径向半径不是特别大时，用其平均半径R 代替有效半径。

通常车轮受到的地面制动力F与制动器产生的摩擦力矩Tf之间的力学关系可由式（10）表达：

式中：rr为车轮滚动半径。

联立式（9）～（10）得：

3 全轮纵向力分配方法

在制动过程中应用全轮纵向力分配算法，就是在考虑轮胎的最大附着力和车辆执行机构本身条件的约束的基础上，准确地控制每个车轮制动力。所以，从本质上讲，全轮纵向力分配问题就是一个带有线性约束条件的二次规划问题[7]。

考虑到控制的可实现性，确定全轮纵向力分配的目标函数的单轮附着裕度的权重系数：

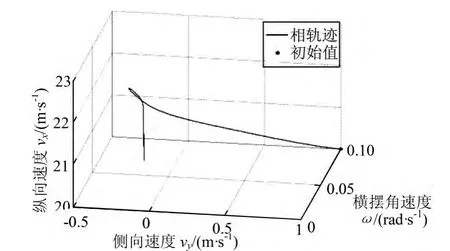
图2 侧向速度、横摆角速度和纵向速度的相空间轨迹曲线

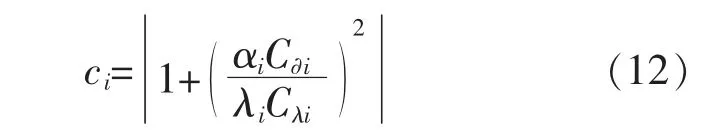
式中：C∂i和Cλi为车轮在静态载荷的作用下的侧偏刚度和纵倾刚度；αi和λi为各车轮的侧偏角和滑移率；μroad为地面附着系数。

考虑到汽车驱动能力的约束：

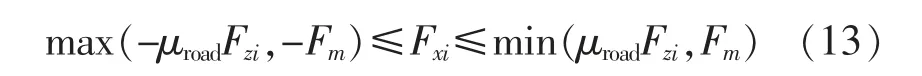
式中：Fm作用在车轮上的纵向力，即不同车轮上轮胎和路面之间的纵向作用力。

联合2个约束和车辆的动力学模型便能建立带有约束的纵向力分配的方程组：

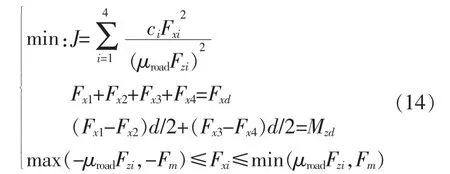
直接横摆力矩控制 Mzd的计算方法如式（15）[1]：

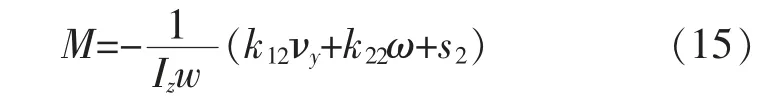
式中：k11，k12，s2为系统参数；w为权重系数。

4 仿真试验分析

结合式（4）～（11）则可利用Matlab 求解式（14）的非线性规划问题。

为了验证所建立的车辆纵向力分配算法的可行性，利用Matlab软件进行仿真实验来进行验证。仿真条件：纵向速度初值vx为20m·s-1，侧向速度初值vy为1m·s-1，横摆角速度初值ω为0.1rad·s-1，前轮转角 δf为0.002rad。

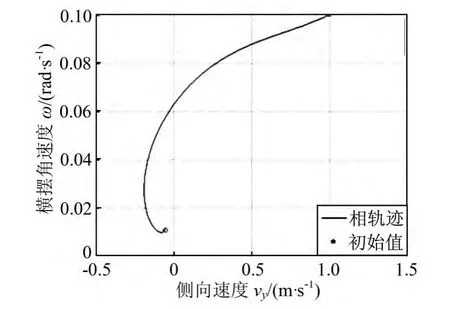
图3 侧向速度与横摆角速度的关系曲线

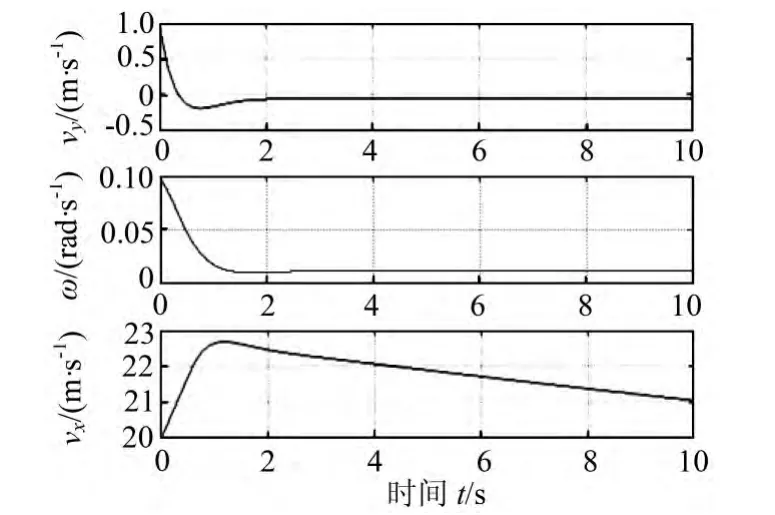
图4 侧向速度、横摆角速度和纵向速度的时间序列

图2～6给出了本组试验的仿真结果。图2为侧向速度、横摆角速度和纵向速度的相空间轨迹曲线。图3为侧向速度与横摆角速度关系曲线。实际上图3为图2在vy—ω平面上的投影。从图中可以看出，由初值点开始，汽车的侧向速度迅速向零点减小，超调达到vy为-0.192 m·s－1后迅速车辆的状态迅速稳定在vy为-0.06 m·s－1附近；横摆角速度 ω则迅速开始减小达到最小值为0.01 rad·s－1后略有增加，达到ω为0.0109 rad·s－1左右；纵向速度 vx则在整个仿真时间内先增大到22.66 m·s－1后减小，在t为10 s时，纵向速度 vx为21.04 m·s－1。

图3中较容易看出汽车的运动状态能够较快的稳定下来，同样的结论也可以在图4中的状态变量的时间序列中得到。

图5给出了在该组仿真条件下，4个车轮分配得到的纵向力。由图中可以看出，由仿真开始，2个后车轮的纵向力由零点开始迅速减小，当t为0.02 s时，左后轮的纵向力Fx3为-889.8 N，右后轮的纵向力 Fx4为-855 N，均达到了最小值；当t为1 s时，左后轮的纵向力Fx3增加到-597.2 N，右后轮的纵向力 Fx4增大到-576.1 N；当t为10 s时，左后轮的纵向力Fx3增加到-595.2 N，右后轮的纵向力Fx4又开始逐渐减小到到-595.2 N。对于2个前轮，当t为0.08 s时，左前轮的纵向力Fx1减小到-1261N，右前轮的纵向力Fx2减小到-1312N，均达到了最小值；当t为1.2s时，左前轮的纵向力 Fx1增加到-966.5N，右前轮的纵向力Fx2增大到-933.1N；当t为10s时，左前轮的纵向力Fx1增加到-975.2N，右前轮的纵向力Fx2又开始逐渐减小到到-975.2N。

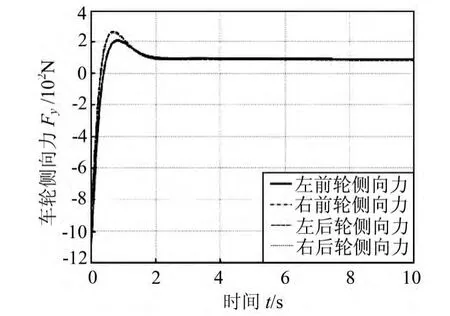
图6 各个车轮的侧向力曲线图

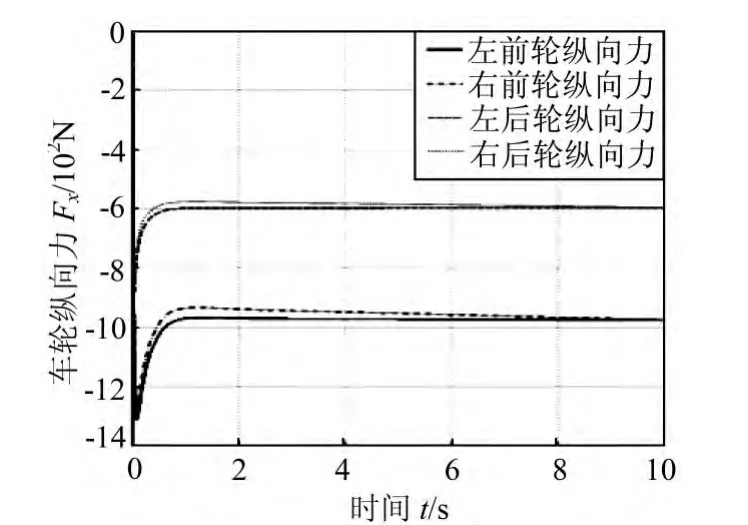
图5 各个车轮纵向力曲线图

图6给出了在该组仿真条件下，4个车轮分配得到的侧向力。由图中可以看出，从仿真开始，当t为0 s时，左后轮的侧向力Fy3由-848.7 N 迅速开始增大，右后轮的侧向力Fy4由-815.4 N 开始增大；当t为0.7 s时，左后轮的侧向力Fy3增加到266.1 N，右后轮的侧向力 Fy4增大到256.4 N；当t为2.4 s时，左后轮的侧向力Fy3减小到88.37 N，右后轮的侧向力Fy4减小到85.72 N；当t为10 s时，左后轮的侧向力Fy3减小到82.97 N，右后轮的侧向力Fy4又开始逐渐减小到82.97 N。对于2个前轮，当t为0 s时，左前轮的侧向力Fy1由-1094 N 开始增大，右前轮的侧向力Fy2由-1052 N 开始增大；当t为0.8 s时，左前轮的侧向力Fy1增大到210.7 N，右前轮的侧向力Fy2增大到203.1 N，均达到了最小值；当t为2.5 s时，左前轮的侧向力Fy1减小到96.75 N，右前轮的侧向力Fy2减小到93.89 N；当t为10 s时，左前轮的侧向力Fy1减小到89.88 N，右前轮的侧向力Fy2又开始逐渐减小到98.87 N。

图7为仿真过程中制动主缸的压力曲线。从图中可以看出，在制动过程中，制动主缸的压力基本保持不变，保持在3.07 MPa。此处值得一提的是，由于本文的研究重点是分析引入制动管路摩擦力约束对全轮纵向力分配的影响，故建立的仿真系统中共有一个主缸用于建立约束条件，而没有建立轮缸执行机构的模型来保证不同车轮的制动力要求，即不同车轮的制动力大小能够无条件实现。

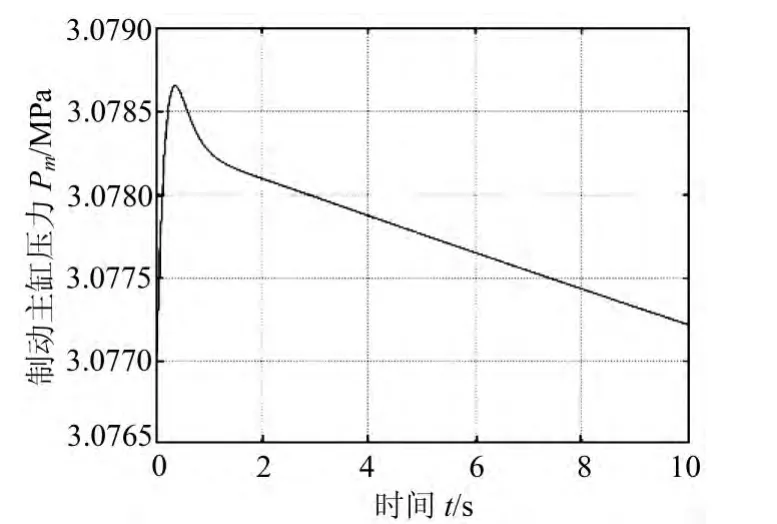
图7 制动主缸压力曲线图

5 结束语

结合车辆动力学模型和制动管路摩擦力模型的约束条件，建立了全轮纵向力优化分配算法，并利用Matlab软件对该分配模式进行了仿真验证和分析。仿真结果表明：该分配算法能够有效进行轮胎力优化分配，以保持车辆运转的稳定。

[1]Esmailzadeh,E.,Goodarzi,A.,Vossoughi,G.R..Optimal yaw moment control law for improved vehicle handling[J].Mechatron,2003,13（7）∶659-675.

[2]M.Mirzaei.A new strategy for minimum usage of external yaw moment in vehicle dynamic control system[J].Transportation Research Part C,2010,18∶1-12.

[3]Ossama Mokhiamar,Masato Abe.How the four wheels should share forces in an optimum cooperative chassis control[J].Control Engineering Practice,2006（14）∶295-304.

[4]喻凡，李道飞.车辆动力学集成控制综述[J].农业机械学报，2008，39（6）：1-7.

[5]One E,Hattori Y.Vehicle dynamics integrated control for four-wheel-distributed steering and four-wheeldistributed traction/braking systems[J].Vehicle system dynamics，2006，44：139-151

[6]李道飞.基于轮胎力最优分配的车辆动力学集成控制研究[D].上海：上海交通大学，2008.

[7]邹永才，罗禹贡，李克强.基于全轮纵向力优化分配的4WD 车辆直接横摆力矩控制[J].农业机械学报，2009，40（5）：1-6.

[8]刘力，罗禹贡，李克强.基于动态目标调整的汽车全轮纵向力分配的研究[J].汽车工程，2010，32（1）：60-64.

[9]郭孔辉，刘溧，丁海涛，李玉璇.汽车防抱制动系统的液压特性[J].吉林工业大学学报：自然科学版，1999，29（4）：1-5.

[10]邓红星.汽车制动管路压力波动效应研究[D].哈尔滨：东北林业大学，2009.

[11]王宪彬，邓红星，王岩斐.基于波动负载装置的液压管路特性分析[J].湖北汽车工业学院学报，2013，27（1）：48-52.

[12]张鸣远.流体力学[M].北京∶高等教育出版社，2009∶334-336.