两种典型桅杆的多极化RCS统计分析❋
2014-11-28杜晓佳李晓明
杜晓佳 李晓明
(中国舰船研究设计中心 武汉 430064)
1 引言
舰船雷达隐身技术是指:在一定威胁区域内降低舰船的雷达信号反射特征,即雷达反射截面积(Radar Cross Section,RCS),用字母σ表示,从而降低其被识别和跟踪的概率[1],有效提升舰船在海战中的突防能力和生存能力,是现代海战取胜的关键因素之一。
桅杆系统一般处于水面舰船结构的最高位置,受地球表面的弯曲效应的影响,它是早期被雷达探测的主要散射源之一,因而桅杆系统将直接影响到全舰雷达隐身性能[2]。舰船的隐身设计目前采用的是全船RCS指标分配方法,研究设计人员在隐身设计中一般把桅杆作为独立部件进行研究[3]。

图1 桅杆为重要雷达反射源
针对目标RCS在不同极化工况下的散射特性存在差异的特点,目前雷达常常综合利用各种极化组合方式进行目标探测[4~5]。例如飞行目标其水平极化RCS一般大于垂直极化,所以众多对空雷达选择水平极化工作方式[6]。随着战场电磁环境的日趋复杂,在面对不同的雷达极化信息时,桅杆如何进行合理的隐身设计面临诸多挑战[7]。
封闭式桅杆能够较好地满足隐身要求因而被广泛采用,如英国45型驱逐舰。由于桁架式桅杆质量较小,重心较低,便于雷达天线等仪器的布置和维修,目前日本金刚级和美国伯克级等驱逐舰依然采用桁架式桅杆。本文以桁架式和封闭式两种桅杆的缩比模型为研究对象,基于快速多极子方法(FMM),参照有关规范和文献,对其在不同极化情况下的RCS计算结果进行统计和分析,讨论了雷达波极化的影响,分析每种桅杆在各种极化雷达波的隐身效果,本文的研究对实际桅杆的隐身设计及优化具有参考意义。
2 舰船RCS基本统计量研究
为了直观分析和研究舰船的多极化RCS起伏特性,可采用一些统计参数来表述,诸如均值、标准差、极大值、极小值和极差以及偏度系数、峰度系数等。本文将这些RCS统计参数分为三类,即代表RCS集中趋势的统计量、代表RCS离散程度的统计量和代表RCS分布形态的统计量。
2.1 代表RCS集中趋势的统计量
代表RCS集中趋势的统计量包括舰船雷达散射截面平均值、总雷达反射截面、中值和众数等,它可以用来表示RCS的分布位置和一般水平。我国现行标准《舰船雷达散射截面测量方法》(HJB 180—98)对这些统计量给出了明确定义,主要有:
1)舰船雷达散射截面平均值:一定测量舷角范围内测量的雷达散射截面积的算术平均值。设角扇形范围内的数据长度为N,则雷达散射截面平均值为

RCS平均值是舰船RCS中最常用的评估标准,与每一个角度RCS数据都有关,较可靠稳定,反映的隐身性能信息最充分。
2)舰船总雷达反射截面:对舰船水平全面方位均匀角度间隔雷达散射截面测量后,去掉0°、90°、180°和270°四个特征方向±4.5°内的测量值,其余各方位雷达散射截面的算术平均值。
3)舰船雷达散射截面概率值(众数):一定测量舷角范围内测量的雷达散射截面(依次从小到大排列)占一定百分比点数中的最大值,其中50%概率值又称中值。
2.2 代表RCS离散程度的统计量
当桅杆的RCS分布越不稳定,其各角度的RCS计算结果的离散程度越大,这些RCS数据的可靠性就越差。
1)最大值、最小值和极差:在评估角域内的舰船RCS的极大值σmax和极小值σmin分别定义为
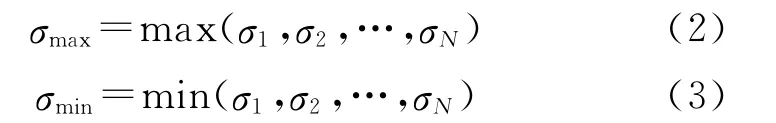
最大值σmax反映的是舰船处于最不利探测角度时产生回波强度。评估区域各角度下的RCS最大值与最小值的差值称为极差σL,它表示这个评估区域内RCS的取值范围:

2)标准差:可反映个体间的离散程度,其中某一角区段的RCS标准差定义为

标准差还可应用于回归分析、正态分布检于、误差分析、评价RCS精度、求取偏度系数和峰度系数等。
2.3 代表RCS分布形态的统计量
RCS序列总体密度函数的图形特征可用偏度系数和峰值系数来描述,对于长度为N、均值和标准差分别为和的RCS序列(i=1,…,N),其偏度系数g1和峰度系数g2定义如下

偏度系数g1反映的是RCS序列密度函数的偏斜程度,其中g1<0、g1=0和g1>0所对应的分别叫作负偏态(峰值向大于方向偏)、正态和正偏态(峰值向小于方向偏)。峰度系数g2可以表示RCS序列密度函数的曲线峰形的相对高低程度或尖平程度,其中g2>0、g2=0和g2<0分别对应为尖峭峰、正态峰和平阔峰。正的峰度系数说明RCS序列更集中,有比正态分布更长的尾部。
3 桅杆电磁散射模型计算设定
3.1 桅杆电磁散射缩比模型
雷达散射截面既与桅杆的几何和材料参数有关,又与雷达波的频率、极化方向和波形等有关[8]。在对这两类桅杆进行电磁反射计算之前,对桅杆进行相应简化,只考虑桅杆主体及雷达承载平台,不考虑雷达天线、信号灯及喇叭等结构的影响。简化后的这两类桅杆模型如图2~图7所示,缩比后这两个桅杆电磁模型高度均为1m。在进行桅杆雷达RCS计算时,暂不考虑隐身涂层影响,桅杆可能布置有频率选择材料FSS,将FSS假定为全反射,即假定桅杆模型均由理想导体PEC材料组成。

图2 桁架式桅杆几何模型

图3 封闭式桅杆几何模型
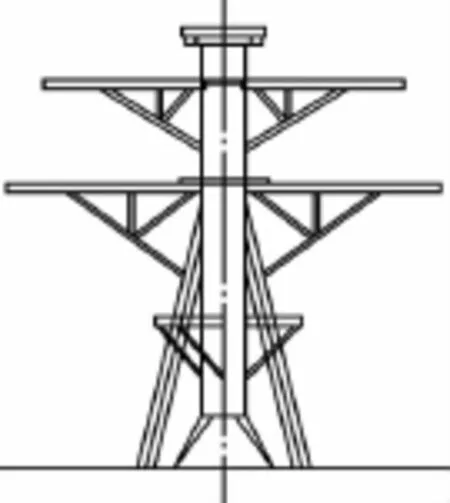
图4 桁架式桅杆前视图

图5 封闭式桅杆前视图

图6 桁架式桅杆上视图

图7 封闭式桅杆上视图
在测量舰船RCS时,雷达天线中心至舰船水线部分连线与它的海平面投影之间的夹角不超过0.5°。因此本文在进行桅杆RCS评估时只针对沿水平面进行传播的雷达波展开,测量舷角以船头方向为0°角,以逆时针增量为正,角采样间隔为1°。
因此对于舰船来讲,最重要的隐身特性指标就是其单站的RCS分布。对舰船进行探测的雷达多处于S、C、X和Ku波段,本文只针对X频段下的入射波进行桅杆单站RCS计算,取该频段的中心频率对应的波长3cm作为雷达入射波长。
舰船所处自然环境较为复杂,波浪载荷或风载荷将使舰船发生运动,同时海浪引起的海杂波易对雷达的探测产生影响[9],会导致预估RCS值与实际测量存在差别,本文只选取了舰船最普遍的环境条件,即静止在海面这种工况进行了分析。
3.2 桅杆电磁反射计算方法
电大尺寸结构的RCS可通过快速多极算法(FMM)、时域有限差分法(FDTD)、物理光学法(PO)、几何光学法(GO)等方法进行求解。本文在保证计算速度的基础上,为满足精度需求,采用快速多极子算法作为桅杆雷达散射截面的计算方法。快速多极子方法是美国Yale大学的Rokhlin在上世纪80年代末提出的,它是基于矩量法(MoM)的迭代法进行加速的快速计算方法,相对于高频近似法具有更广的应用范围和更佳的计算精度。C.C.Lu和W.C.Chew等人将该方法应用于计算电大复杂目标的电磁散射问题[10]。
快速多极子方法基本原理是:将目标进行离散得到的子目标分组,其中任意两个子目标间的相互耦合根据它们所在组的位置关系采用不同的处理方法。自身组和相邻组采用直接矩量法计算,非相邻组采用聚合-转移-配置方法计算。所有源散射体i对场散射体j的贡献用快速多极子方法表达为

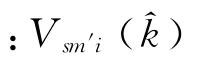
4 桅杆多极化RCS统计结果分析
在波长为0.03m,采用交叉极化VH与共极化(HH或VV)三种极化方式的雷达波照射下,利用快速多极子方法求得的两种桅杆缩比模型RCS随着姿态角的变化曲线如图8所示,其横坐标代表为方位角,其他参数如图8所示。
从图8中可以看出,对于这两类桅杆,在三种极化方式下RCS均随雷达波入射姿态角有较大起伏。同时对于这两类桅杆,交叉极化VH与共极化(HH或 VV)相比,明显较低,相差约有5dB~20dB,很明显以交叉极化方式进行工作的雷达并不能很好地对桅杆一类的目标进行探测。因此在对桅杆的RCS进行数值计算时,可以忽略交叉极化这种工况。

图8 桅杆模型的RCS分布曲线
对于桁架式桅杆,在四个特征值角度0°、90°、180°和270°附近,HH极化方式有明显的四个较突出的高峰值点,而相应的VV极化方式则相对较弱。对于封闭式桅杆,共极化分量(HH和VV)的RCS特性是基本一致的,RCS在峰值点的位置和大小上基本相同。
表1为桁架式和封闭式桅杆缩比模型在共极化方式下的RCS统计结果,从表中可以看出:
对于不同的极化方式,桁架式桅杆RCS的平均值和总RCS值均大于封闭式桅杆,其中桁架式桅杆总RCS值约为封闭式桅杆的两倍,可见封闭式桅杆的整体的隐身效果更好。
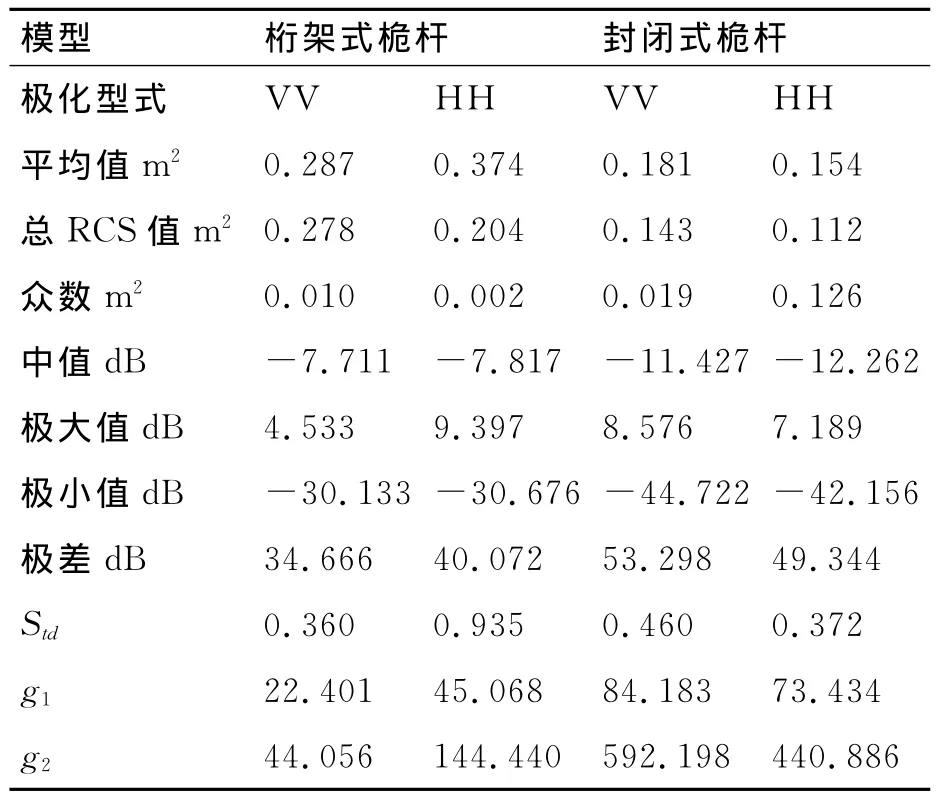
表1 桅杆模型的RCS统计参数
对于桁架式桅杆,其在HH极化方式下RCS平均值比VV极化时的RCS平均值较大,而封闭式桅杆则不同,VV极化方式下RCS平均值和总RCS值均较大于HH极化方式。可见在不同极化方式下两种桅杆的RCS分布均存在差异,在进行桅杆隐身设计不能只考评单个极化方式。
总雷达反射截面普遍比平均值要低,尤其是对于HH极化工况下的桁架式桅杆,总雷达反射截面接近于平均值的二分之一,可见对于这两类桅杆模型四个特征方向±4.5°内的RCS值相对于其他区域的RCS相对较高,在进行RCS评估分析时应重点或单独分析。
除封闭式桅杆HH极化工况,其他工况下桅杆RCS数据的众数均较低0.02m2,同时这两类桅杆在各极化方式下的RCS数据中值较低,这说明在大数角度情况下这两类桅杆RCS数据的水平比较低。
封闭式桅杆在评估区域内的极大值并没不一定小于相同极化下的桁架式桅杆,在当舰船处于最不利角度时封闭式桅杆的隐身效果并不一定占优。在共极化方式下,这两类桅杆RCS数据的极差σL均大于30dB,可见这两类桅杆RCS随观察角变化的幅值是十分大的。封闭式桅杆在HH极化工况下的标准差(0.935)相对于其他工况下桅杆的标准差(均在0.3~0.5之间)较大,可见该工况下的各角度下的RCS离散程度比其他工况较高。
这两类桅杆在各极化方式下,偏度系数g1均大于0,数据分布不对称性,为正偏态,RCS序列密度峰值向低于平均值方向偏,这与概率值和中值分析得到大数角度情况下这两类桅杆RCS相对比较低的结论相似。从表中可以看出,这两类桅杆在各极化方式下峰度系数g2均相对较大于0,说明RCS序列密度函数的曲线峰形尖锐,RCS分布区域比较集中,有比正态分布更长的尾部。
下面分析VV极化方式和HH极化方式下的RCS比值,这两类桅杆在各角度下σVV/σHH结果如图9所示,统计结果如表2所示。

图9 VV和HH极化方式下的RCS比值
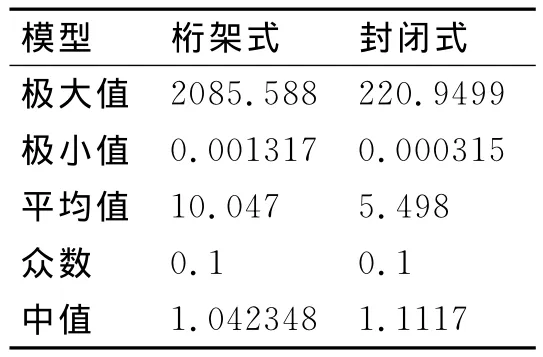
表2 RCS比值统计参数
从图中可以看出这两类桅杆的σVV/σHH随着姿态角变换剧烈。这两类桅杆在评估区域内σVV/σHH的中值接近1,说明在大多数角度情况下两类桅杆在两种同极化工况下的反射能量相差不大。
当雷达沿水平方位角为0°或180°附近传播时,即探测雷达处于桅杆的正前方和正后方,这两类桅杆在两个方向的σVV/σHH均小于1,且σVV/σHH在评估区域内的众数为0.1,可见在该电波入射下,水平极化更有利于舰船桅杆前向或后向散射情况下的目标分类识别,在进行桅杆隐身设计时应针对其进行改善。
5 结语
本文首先对舰船RCS基本统计量进行归类和分析,然后针对桁架式和封闭式桅杆缩比模型为研究对象,基于快速多极子方法,对其在不同极化情况下的RCS计算结果进行统计和分析,具体结论如下:
1)将RCS统计参数分为三类,即代表RCS集中趋势的统计量、代表RCS离散程度的统计量和代表RCS分布形态的统计量,每一类统计量表示不同的RCS统计特征。
2)桁架式和封闭式桅杆的RCS均随雷达波入射姿态角有较多的起伏,且幅值较大。在进行桅杆的隐身性能评估时,可以忽略交叉极化这种工况。封闭式桅杆比桁架式桅杆的整体的隐身效果更好,但在当舰船处于最不利角度时封闭式桅杆的隐身效果并不一定占优。
3)与VV极化相比,HH极化下的桁架式桅杆缩比模型在特征值角度方向有明显的高峰值点,而封闭式桅杆并不存在这一现象。在不同极化方式下两种桅杆的RCS分布均存在差异,在进行桅杆隐身设计或分类识别时应不能只考评单个极化方式。
4)在大数角度情况下这两类桅杆在两种同极化工况下的反射能量相差不大,RCS数据的一般水平比较低。但在部分角度上,尤其是四个特征方向附近,这两类桅杆的RCS值较高,RCS序列密度峰值向低于平均值¯σ方向偏,且曲线峰形尖锐。本文的研究对实际桅杆的隐身设计及优化具有参考意义。
[1]林忆宁.21世纪水面战舰设计的新攻略-隐身性和战斗力兼优[J].船舶工程,2004,26(5):1-7.
[2]吕明云,黄敏杰,武哲.封闭式隐身桅杆的初步设计与效果评估[J].电波科学学报,2010,25(5):833-838.
[3]吴启华.角度、频率因素对隐身桅杆RCS测量结果影响研究[J].舰船工程研究,2007(4):40-45.
[4]李晓良,胡程,曾涛.多极化前向散射RCS分析及其对目标分类识别的影响[J].电子与信息学报,2010,32(9):2191-2196.
[5]匡磊,吴先良.不同极化方式下复杂目标高频区的RCS计算[J].安徽大学学报,2004,28(3):43-49.
[6]胡瑞卿,韩允.极化方式及其在电子对抗中的选择运用[J].现代电子技术,2010(22):120-122.
[7]刘勇.动态目标极化特性测量与极化雷达抗干扰新方法研究[D].长沙:国防科学技术大学,2011:4-8.
[8]程子君,吴启华.隐身桅杆与主船体耦合RCS特性研究[J].中国舰船研究,2011,6(3):45-48.
[9]Alan B,Bill D,Alan W.Radar and arpa manual[M].Second Edition.UK:Butterworth Heinemann,2005:172-180.
[10]J M Song,W C Chew.Fast multipole solution of three dimension integral equation[J].IEEE Trans.On Antennas and Propagation,2005,53(2):793-99.
