基于现场监控量测数据的反分析法确定隧道二衬支护时机

2014-11-27李宝平高诗明

铁道建筑 2014年8期

李宝平，高诗明，王睿，秦威

(西安工业大学建筑工程学院，陕西西安 710032)

隧道工程二次衬砌支护时间直接影响隧道结构的安全与稳定［1-3］，如何确定合理的二次衬砌施作时机始终是隧道工程的热点问题［4-6］。对于浅埋、软弱围岩隧道等围岩条件较差的隧道，适时地施作二次衬砌尤为重要。倘若二次衬砌施作过早，围岩应力不能得到有效释放，结构容易遭受破坏;施作太晚，可能会因为初期支护不能抑制隧道变形，从而导致围岩丧失自承能力，最终导致隧道坍塌。

现阶段国内外许多专家学者主要应用基于现场实测分析的经验法以及基于现场监控量测数据的反分析法，或基于力学理论的数学计算解析法、数值模拟法研究隧道二衬支护的时机。本文基于西施坡高速公路隧道工程实例，采用对现场监控量测数据的反分析，利用变形速率准则和极限位移准则分别确定隧道二衬支护的时机，结合最小支护抗力原则，最终确定隧道二次衬砌支护的最佳时机。

1 工程概况

西施坡隧道位于商洛市商州区北面，为双向4车道分离式隧道。左洞起止里程:ZK4+514—ZK5+062，长548 m，起止点高程分别为776.269，769.568 m;右洞起止里程:YK4+498—YK5+053，长555 m，起止点高程分别为775.990，767.665 m。隧道为直线单向纵坡隧道，左洞隧道纵坡设计为－1.22%，右线隧道纵坡设计为－1.50%。隧道最大埋深左线约为86 m，右线约为87 m。洞身有几处埋深较浅，最小埋深约为14 m。隧址区植被发育。左洞入口段、右洞出口段地形较陡，为残积土和强风化砂岩、泥岩互层。残积土疏松杂乱，大部分基岩裸露，坡体风化强烈，岩石产状约为180°∠20°。右洞入口、左洞出口处地形较缓，部分基岩裸露，山坡倾向东，岩体为中风化泥岩、砂岩互层。岩体小裂隙发育，岩体较破碎，坡角约为20°～30°，岩石产状约为220°∠30°。

2 基于现场监控量测数据的反分析法对隧道二衬支护时机的确定

通过对现场实测数据进行回归分析，确定同时满足变形速率准则和极限位移准则的二衬施作时机，结合最小支护抗力原则，确定隧道二次衬砌最佳支护时机。

2.1 变形速率准则和极限位移准则

变形速率准则:根据《公路隧道施工技术规范》(JTG F60—2009)规定，当拱顶下沉速率＜0.07～0.15 mm/d时，隧道适合施作二衬支护。隧道初期支护后，隧道岩土体的变形量随时间而逐渐变大，经过一定的时间，当时间为t1时刻，隧道变形量趋于某一定值y1。此后，随时间推移，变形速率减小，直至变形速率趋于0。拱顶的变形速率基本稳定在0.07～0.15 mm/d范围内，根据变形速率准则可以确定t1时刻为二衬支护时机。隧道变形时程曲线［7］如图1所示。

以YK4+532为例，根据变形速率准则，并结合西施坡隧道现场监测数据，拱顶下沉速率＜0.07～0.15 mm/d时，该隧道断面二衬支护时机为25 d，距掌子面63 m(见表1)。基于变形速率准则，ZK4+586，YK4+532，YK5+012，ZK5+034 断面分别在27，25，22，21 d后适合施作二衬支护，故隧道二衬支护时机为21～27 d，距掌子面距离为52～68 m。

表1 隧道支护时机

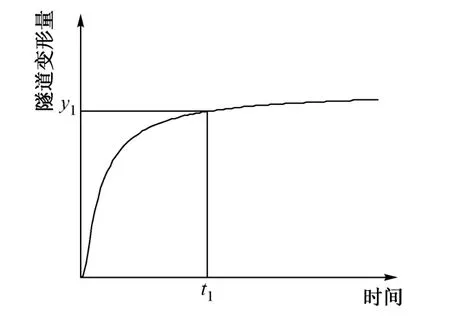
图1 隧道变形时程曲线

极限位移准则:根据《锚杆喷射混凝土支护技术规范》(GB 50086—2009)规定，已产生的各项位移达到各项预计位移总量的80% ～90%(根据现场监测情况综合分析，当实测位移为0.8倍的极限位移时，施作二次衬砌比较合理)时，隧道适合施作二衬支护。

根据隧道实测拱顶沉降数值，通过MATLAB软件对变形测试数据进行统计、回归分析后，采用指数函数y=A e－B/x对拱顶沉降曲线进行拟合分析，求得位移回归方程。对西施坡隧道ZK4+586，YK4+532，YK5+012，ZK5+034断面拱顶位移监测数据利用MATLAB软件进行回归分析，结果如图2所示。

以ZK4+586为例，MATLAB分析拱顶沉降的极限位移公式为:y=93.02 e－5.18/x。当x趋向无穷时，极限位移值为93.02 mm，其中拟合相关系数R=0.91。该断面二衬支护时机为隧道开挖后第23 d，距掌子面58 m，具体见表1。

根据隧道极限位移准则，ZK4+586，YK4+532，YK5+012，ZK5+034 断面分别在23，21，26，19 d 后满足二衬支护条件，故二衬支护时机为19～26 d，距掌子面距离为47～66 m。

图2 断面拱顶沉降拟合曲线

建议取两种准则下的时间交集作为二次衬砌支护时机，即二次衬砌最佳支护时机为初期支护后21～26 d，距掌子面距离52～66 m。

2.2 最小支护抗力准则

如果隧道在开挖后，围岩不发生破坏(即隧道围岩本身有很强的稳定性)，则隧道无需进行二衬支护。倘若对隧道进行支护，那么支护结构也仅仅起安全储备作用。正常情况下隧道开挖后，围岩会发生不同程度的破坏，继而涉及的问题是至少需要有多大的抗力，支护结构才能阻止围岩破坏，这个抗力就是最小支护抗力。只要知道最小支护抗力，就可以选择合理的二衬支护时机。

在取得支护抗力数值比较困难的情况下，假设可以利用隧道拱顶有效应力研究二次衬砌，替代阻止围岩破坏的支护抗力。通过分析隧道拱顶有效应力，将支护抗力最小的时机作为二次衬砌施作时机。

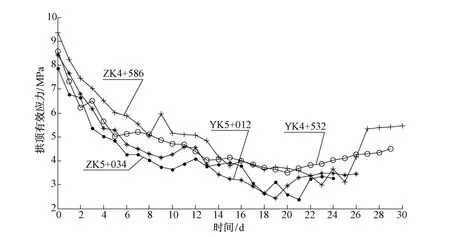
图3 拱顶有效应力随时间变化曲线

围岩拱顶有效应力随时间变化趋势如图3所示。以YK5+012断面为例，拱顶有效应力随隧道的开挖快速变小，在隧道初期支护结束后第9 d，有效应力减小为4.13 MPa。之后其值小幅度反弹，紧接着减小，到初期支护结束后第19 d，拱顶有效应力减小到最小值2.43 MPa。随时间推移，有效应力以很小的速率逐渐增大，25 d后近似趋于3.62 MPa。根据隧道支护抗力最小准则，ZK4+586，YK4+532，YK5+012，ZK5+034断面分别在23，20，19，21 d后满足二衬支护条件，故二衬支护时机为19～23 d，距掌子面距离为47～58 m。

从拱顶围岩受力情况分析，考虑有效应力时，二次衬砌最佳支护时机为开挖后19～23 d，略小于基于变形速率准则和极限位移准则确定的二次衬砌初期支护完成后21～26 d的支护时机，这主要是因为隧道开挖过程中应力释放速度远远大于位移发展速度。综合考虑应力释放速度和位移速度的影响，建议二次衬砌最佳支护时机为开挖后约21～23 d，与拱顶位移发展分析所得基本一致，证明了可以采用拱顶有效应力替代支护抗力研究隧道衬砌。