铁路小半径大跨度曲线连续刚构桥设计分析

文 强

(中铁第一勘察设计院集团有限公司，陕西西安 710043)

1 工程概况

兰州至中川铁路于兰州市西固区石岗镇附近跨越黄河干流，桥址处主河槽宽约300 m。主流靠左岸，左岸为陡峻山崖，相对高差30 m左右，右岸滩地宽阔平坦，高出主河道约8 m。河道常年流水，平时水深4～6 m左右。桥址处黄河流域面积约220 000 km2，设计流量采用:Q1%=6 500 m3/s，Q0.33%=7 340 m3/s。线路法线与黄河主槽中泓线夹角2°，主桥采用(80+2×120+80)m预应力混凝土连续刚构，位于R=800 m的圆曲线上，主桥总体布置如图1所示。设计标准为双线客货共线铁路，时速160 km/h，活载等级为“中—活载”。桥址地震动峰值加速度为0.238g(相当于地震基本烈度八度)，地震动反应谱特征周期0.45 s。桥址主要地层为:第四系全新统杂填土、冲积粉土、砂质黄土、粉砂、细砂、粗圆砾土、卵石土，基底为第三系中新统泥岩夹砂岩、砂岩夹泥岩局部夹有砾岩。

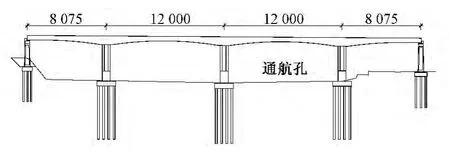
图1 西固黄河特大桥主桥总体布置(单位:cm)

2 主桥结构构造

2.1 主梁［1-3］

主桥位于半径800 m曲线上，主梁采用曲梁曲做法，梁端线与线路法向平行。箱梁采用单箱单室变高度变截面结构，箱梁顶宽11.4 m，底宽6.7 m。主梁计算跨径(80+2×120+80)m，梁全长401.5 m。梁高按2次抛物线变化，中支点处梁高8.8 m，跨中及梁端梁高4.6 m，边支座中心线至梁端0.75 m。箱梁顶板厚0.40～0.65 m，底板厚0.5～1.2 m，腹板厚0.5～1.0 m，悬臂端部厚0.25 m，根部厚0.65 m。为了提高曲线箱梁的截面抗扭能力，在箱梁腹板顶、底部分别设0.9 m×0.3 m及0.6 m×0.3 m倒角，并在支点、刚构墩顶及主跨跨中处设置横隔墙。主梁横截面如图2所示。

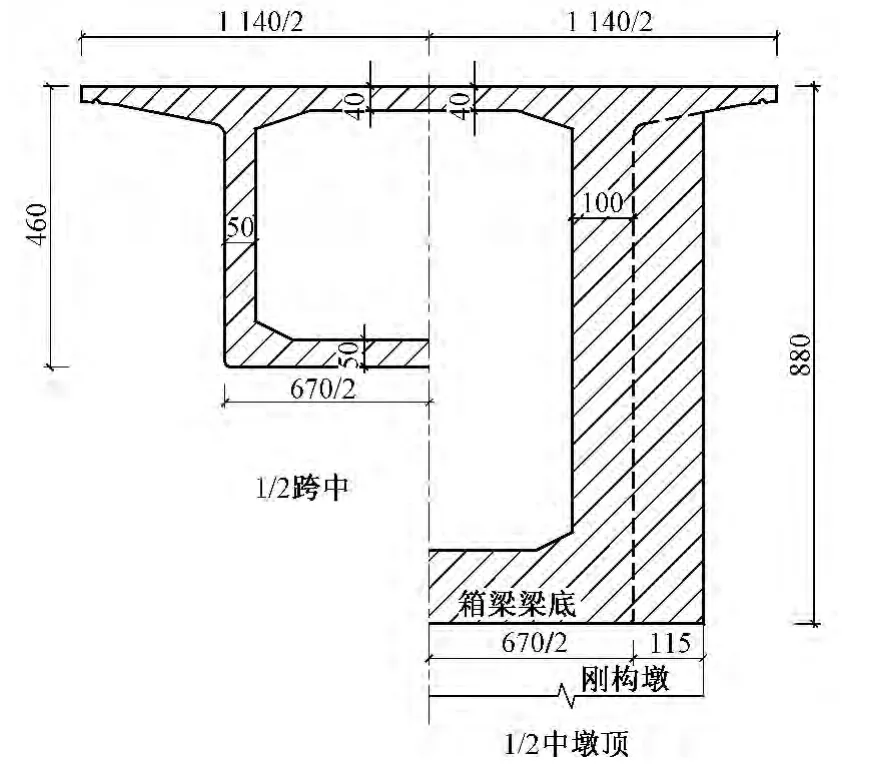
图2 主梁横截面(单位:cm)

主梁按纵、横、竖三向预应力体系设计，纵向按全预应力设计。主梁采用悬臂灌注施工法。

2.2 桥墩及基础［4］

主桥中间3个桥墩均为刚构墩，高度依次为37.0，38.0，36.5 m。如采用圆端空心桥墩，则纵向刚度过大，地震作用随刚度增大相应增大，墩身配筋困难，浪费材料且造型笨重。因此，刚构墩采用板式双壁墩，壁厚2.2 m，双肢中心距6 m。墩底高出百年水位2 m以下部分采用带弧形尖角的实体墩，以满足破冰及防撞要求。桥墩造型轻巧美观，且节约材料、受力合理，如图3所示。边墩采用圆端形空心桥墩。

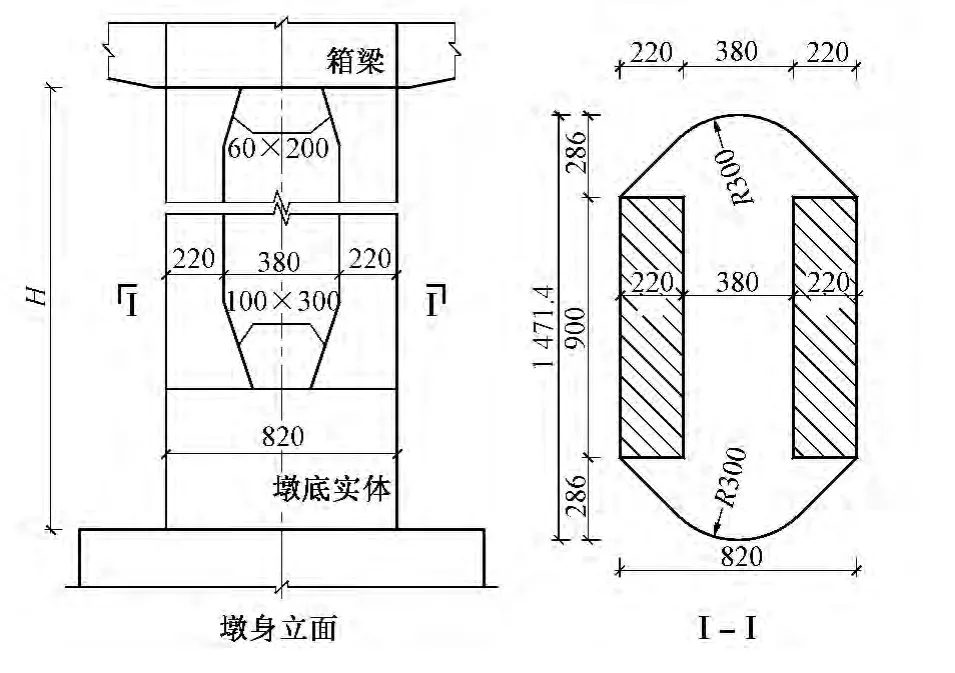
图3 刚构墩构造(单位:cm)

基础均采用钻孔灌注桩基础，中墩(刚构墩)采用16根直径2 m桩，边墩采用12根直径1.5 m桩。

3 主桥结构分析

3.1 曲线梁特点

对于直线双线铁路桥梁，在恒载及预应力作用下，由于截面及荷载在横向均对称，对箱梁不会产生扭矩及扭转变形，仅在单线活载作用下有扭转效应。根据以往设计经验，铁路箱梁截面较大，且箱形截面自身抗扭能力较强，一般直线梁在活载下的扭转可忽略。大曲率半径的曲线梁扭转效应较小，一般也可按直线梁设计。但对于半径较小的曲线梁，在恒载、预应力及活载作用下均产生扭转效应，且随半径减小而更加显著，鉴于小半径曲线梁受力的复杂性，其扭转效应不容忽视［5］。

目前对于曲线梁桥的计算理论研究较多，但多数解析方法公式推导太过繁复，不利于掌握，更不利于实际曲线梁桥设计使用，其中梁格系理论较易于理解和使用，计算精度一般能够满足工程需求，故应用较广泛，但需进行扭转修正。本文采用有限元分析方法，针对(80+2×120+80)m预应力混凝土连续刚构桥，分别建立直线、曲线单梁模型及曲线梁格模型，进行对比分析［6-7］。

3.2 静力分析

3.2.1 计算模型

采用MIDAS有限元软件，建立各种计算模型如图4所示。

图4 有限元计算模型

3.2.2 静力计算结果［8-9］

1)运营阶段支反力

对于边支座，在恒载(含预应力次内力及混凝土收缩徐变)作用下，直线梁横向两个支座支反力相等;而对于曲线梁，支座横向按对称布置，则曲线外侧支反力大于内侧，内外侧支反力差值约为其平均值的40%。在主力(恒+活)作用下，内外侧最大支反力差值约为平均值的30%，虽然不会出现受拉，但在选择支座时，如内外侧按相同吨位选择，则需考虑留有足够的富余量，以防止外侧支座承载力不足。

2)刚构墩内力

刚构墩采用钢筋混凝土结构，配筋控制截面为墩顶、墩底截面。表1为不同计算模型在恒载作用下刚构墩墩底内力。

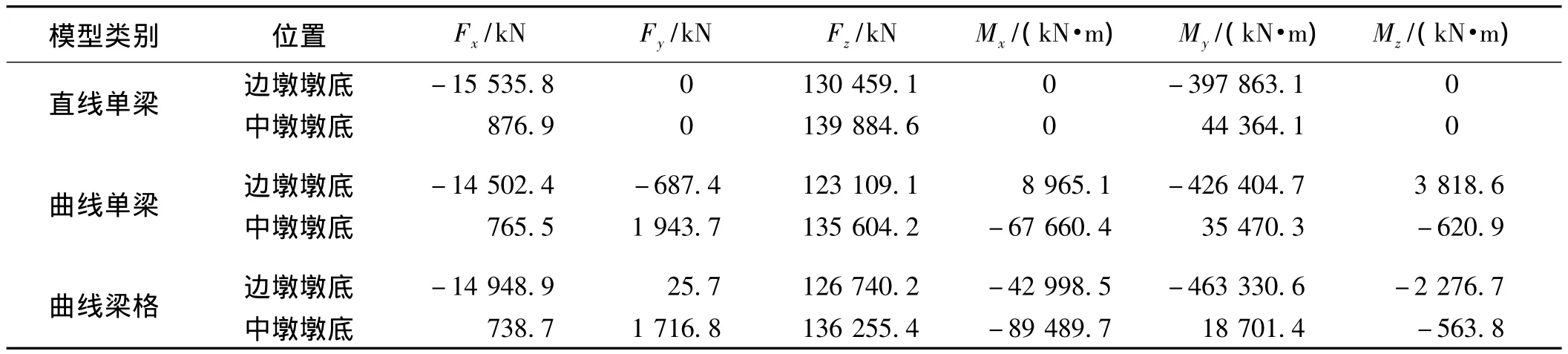
表1 刚构墩墩底截面恒载内力(x，y，z分别代表纵、横、竖向)

从表1中可以看出刚构墩墩底截面上曲线梁有较大的横向弯矩Mx，对于纵向弯矩My，边墩曲线梁较直线梁大，而中墩则略小，曲线梁有扭转效应(Mz)但数值不大，对于竖向压力，则直线梁较曲线梁略大。

3)梁体内力

对于纵向弯矩直、曲线梁在恒载作用下沿梁轴线变化规律一致，负弯矩均在刚构边墩墩顶处达到最大。但最大负弯矩直线梁比曲线梁大10%左右，而中跨跨中弯矩图则基本重合，边跨跨中直线梁略大，如图5所示。活载弯矩包络图直、曲线梁变化规律相同，数值差别不大。故纵向预应力设计按直线梁考虑偏安全。

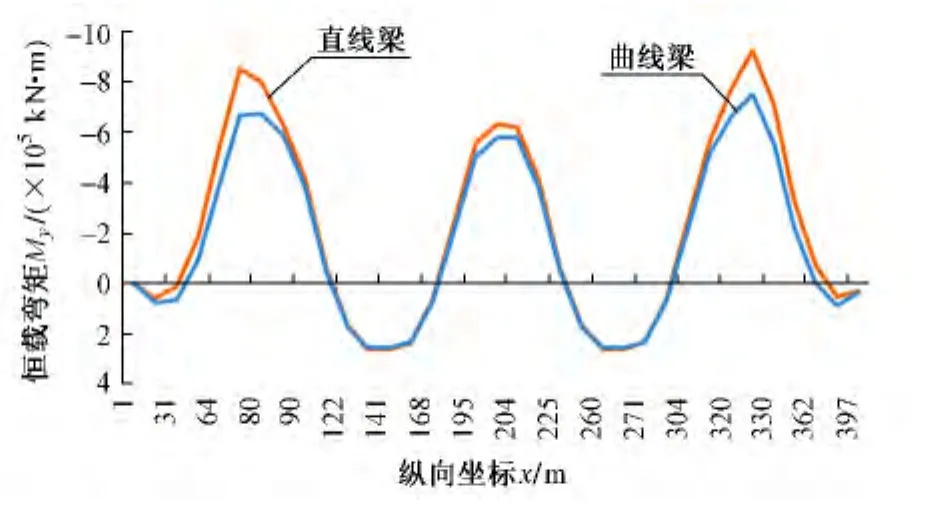
图5 恒载作用下梁体弯矩

对于扭矩，直线梁在恒载作用下无扭矩，而曲线梁在恒载作用下扭矩图在纵向呈反对称形态，在支点处最大，中跨跨中为0，见图6。图7为直、曲线梁在中活载作用下扭矩最大值(正方向)包络图，从图中可以看出，活载作用下直、曲线梁扭矩最大值变化规律基本一致，但直线梁扭矩较曲线梁大，支点处直线梁约为曲线梁的1.5倍。恒载+活载作用下，直、曲线梁轴力相差不大，剪力则支点处直线梁较曲线梁大。可见对于一般的曲线梁，纵向按直线梁计算是可以满足要求且偏于安全的。

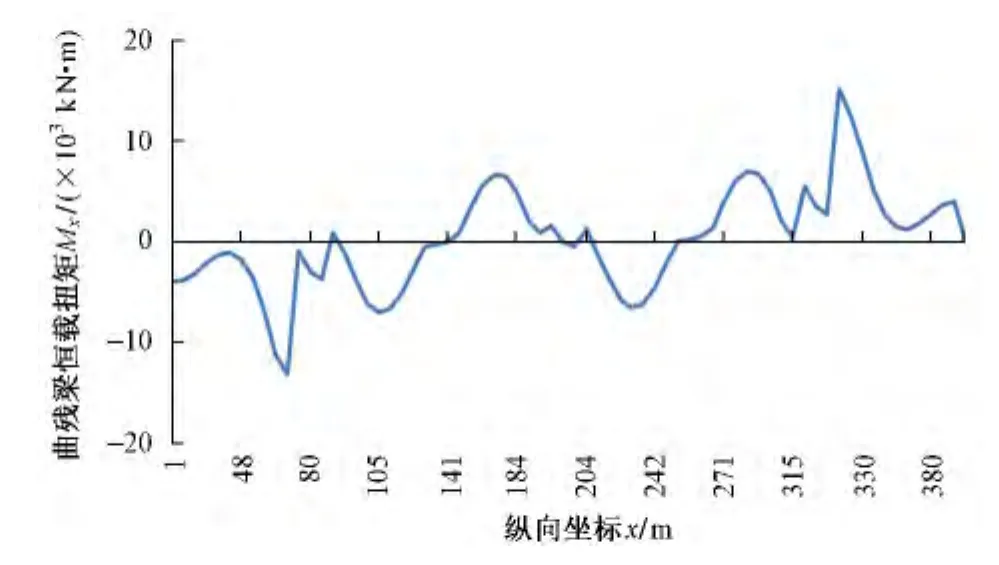
图6 曲线梁恒载作用下梁体扭矩

4)梁体变形

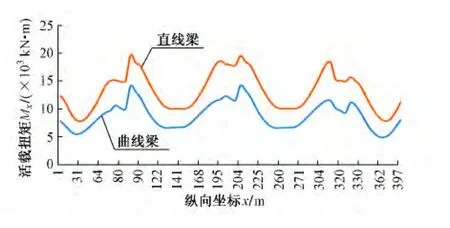
图7 中活载作用下梁体扭矩

分别对直、曲线梁在荷载作用下的竖向、横向及转角等位移分量进行了对比。活载作用下，直、曲线梁竖向最大位移形状及数值基本相当，最大值均出现于中跨跨中，数值约为跨度的1/3 400。对于恒载位移，其最大值均出现在边跨约1/4跨处，直线梁略大。曲线梁在恒、活载作用下，均有横向位移及转角。

5)预应力损失

分别对直、曲线梁的各项预应力损失进行了对比。对于管道摩阻损失，曲线梁由于钢束平弯影响，其损失值比直线梁大，但差值很小，在10 MPa以内;锚具变形及预应力钢束松弛损失，直、曲线梁几乎无差别;弹性压缩及混凝土收缩徐变引起的预应力损失，直线梁大于曲线梁。扣除各项损失后，除顶板合龙束外，其他钢束的有效预应力曲线梁均略大于直线梁。由此可见，对于一般的曲线梁，纵向按直线梁计算是可以满足要求的，且偏于安全。

3.2.3 动力特性［10］

对直、曲线梁建立梁单元模型，考虑实际桩基础刚度，将桥面二期恒载转化为质量，采用迭代法算得主桥前5阶振型如表2。可以看出，直、曲线梁自振周期差别不大，曲线梁略大，振型形状类似。

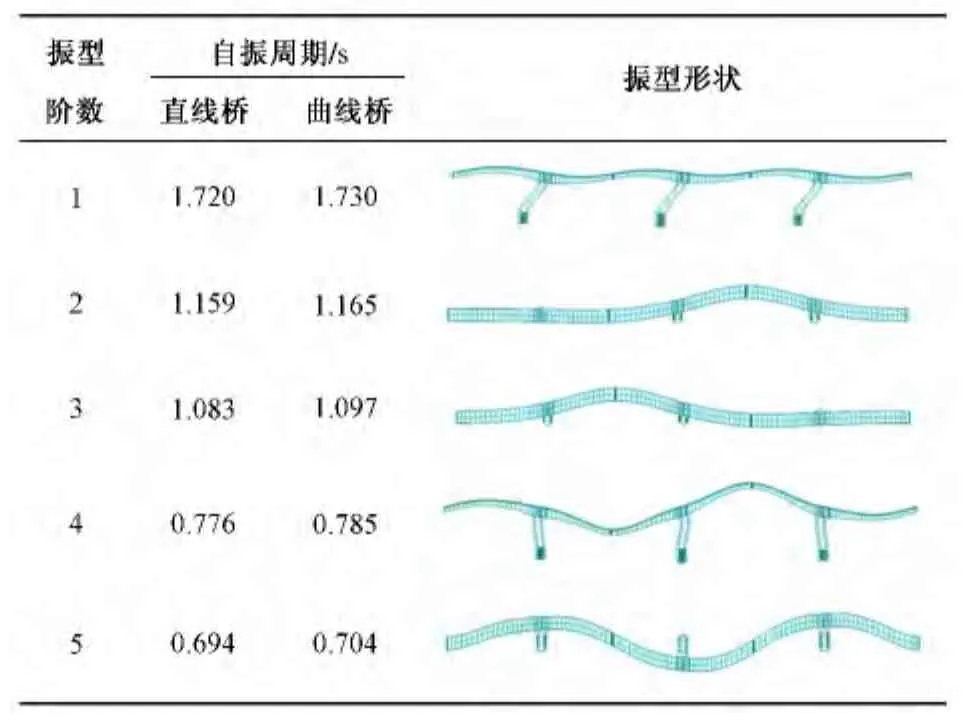
表2 主桥前5阶振型

4 结语

曲线梁桥受力复杂，虽然理论研究较多，但多不便于实际应用，不像直线桥易于理解。且不同的有限元软件计算结果也有较大差异，实际设计中对于较大半径的曲线梁一般按直线梁设计，从以上分析及以往类似工程经验，一般可以满足要求且偏于保守。但对于半径过小的曲线梁，其影响因素较多。有研究表明，圆心角＞30°的曲线梁非线性效应明显。另外，对于曲线梁的温度效应及地震影响分析，由于曲线桥自身结构的复杂性，目前的研究还不够完善，对于曲线桥的深入认识，还有待进一步的研究。

［1］郑健.中国高速铁路桥梁［M］.北京:高等教育出版社，2008.

［2］中华人民共和国铁道部.2000—2010中国铁路大桥资料选编［Z］.北京:铁道部工程设计鉴定中心，2011.

［3］金勇.大跨度铁路连续刚构桥动力特性分析［J］.铁道建筑，2013(11):16-18.

［4］全开华，冯卫军，李云.连续刚构桥梁的延性地震响应分析与应用［J］.铁道建筑，2011(11):23-25.

［5］臧立秋.小半径、大跨度曲线刚构—连续组合箱梁设计研究［J］.铁道标准设计，2012(3):9-12.

［6］邹荣光，夏淦.混凝土弯梁桥［M］.北京:人民交通出版社，1994.

［7］单德山，李乔.高速铁路曲线梁桥的支座布置形式初探［J］.重庆交通学院学报，2001(2):2-5.

［8］中华人民共和国铁道部.TB 10002.1—2005 铁路桥涵设计基本规范［S］.北京:中国铁道出版社，2005.

［9］中华人民共和国铁道部.TB 10002.3—2005 铁路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京:中国铁道出版社，2005.

［10］中华人民共和国建设部，中华人民共和国国家质量监督检验检疫总局.GB 50111—2006 铁路工程抗震设计规范［S］.北京:中国计划出版社，2009.