基于S函数实现的参数自整定模糊PID控制器

2014-11-25鲁改凤卢东伟

华北水利水电大学学报(自然科学版) 2014年4期

鲁改凤，卢东伟，孟波，王佳，鞠阳

(华北水利水电大学，河南郑州450045)

自计算机进入控制领域以来，尤其是数字计算机取代模拟计算机调节器成为计算机控制系统的主要部分以来，不仅实现了软件的PID 控制算法，而且可以采用计算机本身自有的逻辑功能，使数字PID控制技术的应用更加灵活，更加有实用价值. 数字PID 控制技术是日常生产过程中比较普遍采用的一种基本的控制算法，其控制系统在机电、冶金、机械、化工等行业中获得了广泛的应用. 数字式计算机技术结合先进的智能控制理论，二者的综合发展为复杂动态不确定系统的控制提供了一种新的解决途径.利用先进的数字智能控制技术，不仅可以设计出先进的智能PID 控制，而且可以对PID 的参数进行智能整定.自整定的模糊PID 参数控制系统能在控制过程中对不确定的条件、参数、延迟和干扰等因素进行在线的检测后进行确定性的分析，采用模糊推理的方法实现PID 参数KP，KI和KD的在线自整定.此方法不仅保持了一般PID 控制系统对PID 控制参数调节简单、使用方便、鲁棒性强等优点，而且具有比较大的调节灵活性以及适应性，对控制系统中各参数的控制精度比较好，是目前较常采用的一种比较先进的控制系统.

利用MATLAB 方法对模糊自整定的PID 控制系统的参数进行数字仿真，可快速方便地实现多种控制规则，控制参数精度高，使模糊自整定的PID 控制系统的参数控制效率以及准确性得到大大提高［1］.

1 参数自整定模糊PID 控制系统的结构设计

1.1 参数自整定模糊PID 控制系统的结构

参数自整定模糊PID 控制系统的结构主要由2部分组成:一是参数可变的PID 控制器，二是模糊控制系统.其结构如图1所示.

图1 自整定模糊PID 参数控制系统框图

误差e 和误差的变化率de/dt 送入模糊控制器，经过模糊化及模糊运算，得到输出的模糊控制变量，再通过解模糊，得到PID 控制器的3 个控制参数KP，KI，KD，这3 个参数再输入到PID 控制器中，然后再应用于控制对象.

应用模糊集合理论建立控制器参数KP，KI，KD与系统误差绝对值e 和误差变化率绝对值de/dt 之间的二元连续函数关系，通过模糊控制器根据不同的e 和de/dt 在线自整定来确定PID 的3 个参数.以满足不同e 和de/dt 对控制参数的不同要求，从而使被控对象达到良好的性能要求.

1.2 PID 参数整定原则

常规PID 控制算法的离散形式为［3］:

式中:k 为采样序号，k = 1，2，…;u(k)为第k 次采样时刻控制器的输出值;e(k)为第k 次采样时刻的输入偏差值;e(k－1)为第k－1 次采样时刻的输入偏差值;KI为积分系数，KI= KPT/TI;KD为微分系数，KD= KPTD/T.

1)当e 的绝对值较大时，若使PID 控制系统具有较良好的跟踪性能，这时取较大的KP，以及较小的KD，同时为避免控制系统响应出现超调大，这时应对积分的控制作用加以限制，通常取KI= 0.

2)当e 的绝对值处于中间大小时，为使控制系统响应超调较小，此时KP的值应取较小值. 在此种情形下，控制系统中KD的值响应较大，KI的取值应适当.

3)当e 的绝对值较小时，为了使当前控制系统有比较良好的稳定性，KP和KI均应取大值，同时为避免控制系统在预先设定的初值附近出现比较大的振荡，当de/dt 值较大时KD取较小值，通常KD为中等大小.

1.3 各变量在模糊控制器中隶属度函数的确定

由PID 控制系统参数的在线自整定原则可以确定e，de/dt，KP，KI，KD的隶属度函数.PID 参数控制的模糊控制器的输入是2 输入，而输出为3 输出.在控制器中以e 的绝对值和de/dt 的绝对值为输入参数变量，以KP，KI，KD为输出参数变量. 模糊控制器的各个参数变量的基本论域为误差绝对值e = {0，E1，E2，E3}.误差变化率绝对值

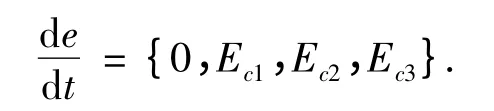
输出KP= {0，UP1，UP2，UP3};

输出KI= {0，UI1，UI2，UI3};

输出KD= {0，UD1，UD2，UD3}.

变量e，de/dt 和KP，KI，KD的论域取值大(B)，中(M)，小(S)，零(Z)，其中Z 采用zmf 隶属度函数，B 采用smf 隶属度函数，S，M 则采用trimf 隶属度函数［4］.

误差比例系数和误差变化率比例系数对模糊控制器的影响也很重要［5］.若误差的基本论域为［－e，e］，误差变化率的基本论域为［－ ec，ec］，误差模糊状态的基本论域为［－ n，n］，误差变化率的模糊状态的基本论域为［－ m，m］，则误差比例系数Ce和误差变化比例系数Cec可由下列公式决定:

参数可变PID 控制器的结构如图2所示.

图2 参数可变PID 控制器结构图

2 大时间延迟系统的参数自整定模糊PID 控制仿真

该次仿真的大时间延迟系统的数学模型为exp(－200 s)×3/(7 000 s +1)，该系统为带有纯滞后的一阶惯性环节.

先在MATLAB 中利用次最优降阶法对该系统进行近似，然后再用Ziegler－Nichols［6］经验公式得到PID 的3 个相关参数KP，KI和KD，即KP=0.485 1，KI= KP/ti= 0.242 5，KD= KPtd= 2.425，然后利用此3 参数构成的连续PID 控制器对exp(－200 s)×3/(7 000 s + 1)这一对象仿真. 经过多次仿真发现KP，KI，KD这3 个参数分别整定在14，0.001，1 600时，系统的性能比较好. 其实现过程有如下3 种:①设定误差的模糊状态的基本论域为［0，10］，设定误差变化率的模糊状态的基本论域为［－ 3，3］;②设定误差的模糊状态的基本论域为［0，3］，设定误差的模糊状态的基本论域为［0，0.003］;③设定误差的模糊状态的基本论域为［0，300］，设定误差的模糊状态的基本论域为［0，0.000 03］.

设定在3 个不同的基本论域并反复调试，假设Ce= 1/50，Cec= 5，KP的作用因子为2，KI的作用因子为1，KD的作用因子为2，然后根据参数整定原则写出模糊控制规则表.

同时为了缩短系统响应时间，在e ＞200 时采用PD 控制，使KI= 0，在e ≤200 时模糊控制器的输出才起作用.

2.1 利用S 函数构建模糊控制器的方法

交互式的模型输入与仿真环境SIMULINK 工具箱是MATLAB 仿真软件的扩展，是一个用来对动态系统进行建模、仿真和分析的软件包，其中S 函数(S-Function)是SIMULINK 提供的内置模块，是SIMULINK 模块的计算机语言描述，用户可以在S函数中编程实现算法.

在利用S 函数构建模糊控制器的过程中，要用Flag = 0，Flag = 2，Flag = 3 这3 种情况.其中Flag =0，调用初始化函数，对该S 函数进行初始化;Flag =2，调用离散状态的更新函数，模糊规则表的建立，各种模糊控制量的建立，都是在该离散状态的更新函数中完成;Flag = 3，输出解模糊后的KP，KI和KD.