基于改进PSO算法的光伏发电系统控制室的选址

穆科磊，李金珏，钱俊良，靳玉凯

(1.华北水利水电大学，河南 郑州450045;2.华能澜沧江水电有限公司 小湾水电厂，云南 昆明675702)

目前，我国在建设光伏发电系统时，主要考虑供电的质量和供电的可靠性，而对控制室选址的经济性考虑较少.控制室的下一级直接针对的是用电负荷，所以，为实现控制室选址的经济性，首先需考虑低压系统的输送能力，控制室要尽可能靠近各个负荷点，并满足从控制室分配出的电能到达用户端的压降不高于其额定电压的5%，以保证用电设备正常工作.控制室的位置还要根据各用电负荷大小的权重来决定.在以往的光伏发电站建设过程中，对于控制室的选择基本不考虑这两个因素，大部分都是在供电地区内寻找方便施工的场所进行建设. 这样不仅浪费了配电线路，增大了投资，并且电能输送距离太远导致用户电压达不到使用要求［1－2］. 笔者基于改进PSO 算法对光伏发电系统控制室的选址模型进行寻优，为确定控制室最佳建设位置提供参考.

1 控制室选址的数学模型

对于控制室的选址问题主要考虑下面3 个因素:①控制室分配给各个用电负荷点的电能大小，它决定着配电系统路径以及相应的电力线材和设备的选择;②控制室到各个负荷点的输电距离，它直接影响到建设的成本和用户所使用电能的质量;③低压配电系统供电半径不超过500 m 的输送能力(实际工程中，供电半径超出500 m，需要进行压降计算，并通过增大相应的导线半径来满足压降的要求，以保证用户的电能质量)［3］.

在一个区域内，控制室内输出的电能供给n 个负荷点，已知每个负荷点i 的位置坐标为(xi，yi)，每个供电负荷点的输送电量为εi，最大允许配电距离为Di，确定控制室的地址坐标为(X，Y)，在满足用户最大输送距离的条件下，总的输送电量最低. 于是，建立光伏发电系统控制室选址的数学模型.

目标函数为

约束条件为

2 改进的PSO 优化算法

在整个优化寻解的过程中，PSO 初始化为一群随机粒子，其最优解通过几轮的迭代求得.在每次的迭代过程中，每一个粒子通过2 个因素进行自我更新，即每个粒子通过取得新的速度而取得新的位置.其中，一个因素是粒子自身寻解过程中个体最优值pbest，往往和算法的局部搜索性能有很大的关系;另一个因素是整个群体所找到的全局最优解gbest，在速度更新中它能带领整个群体向问题的全局最优靠拢.粒子在找到上述2 个最优解之后，分别通过下面的公式来进行自身速度和位置的迭代更新.

式中:Vid为粒子速度;ppresent为粒子当前的位置;c1和c2分别为学习因子或加速常量;φ1和φ2为(0，1)区间内的2 个随机正整数.这样，粒子通过式(3)和式(4)进行不断更新学习，在个体和群体的共同协作下算法可以取得最优解.

粒子群算法同遗传算法类似，都属于随机迭代优化工具类算法，适用于求解大量非线性、多峰值以及不可微的复杂优化问题.然而，基本的粒子群算法存在一定的局限性，尤其在解决复杂的优化问题时，很容易陷入局部收敛［4－6］. 同遗传算法及其他全局算法一样，PSO 应用于高维复杂问题优化时，存在早熟收敛的问题.也就是说，种群在搜索全局最优解的过程中，很容易聚集到一点停滞不动.

为了改善基本粒子群算法的收敛性能，引入惯性权重ω，并对粒子群算法的速度方程(式(3))进行改进，即

粒子群在实际的搜索过程中，惯性权重ω 的大小应随着进化速度的粒子聚集程度而改变，也就是说ω 是h 和s 的函数，即

式中:h 为进化加速因子;s 为粒子的聚集度因子.

粒子群进化速度因子

h 越小，粒子群进化速度越快.如果通过一定的迭代次数后，h 值始终保持为1，这样算法就停滞或者已经搜寻到最优解.

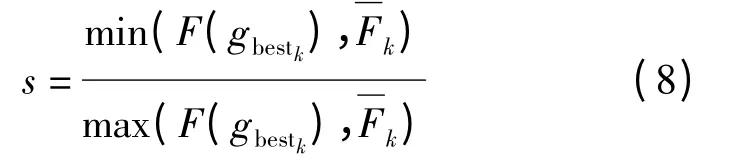
s 取值越大，粒子的聚集程度也越大，其多样性越小.若s=1 时，表示所有的粒子具有同一性，一旦粒子陷入局部最优，搜寻的结果就很难跳出局部极值，算法就会停滞.

在整个粒子群寻优的过程中，进化速度比较快时，即h 比较小，PSO 算法会在较大的搜索空间内持续搜索，粒子就可保持大范围的寻优，当粒子群进化速度变慢时，可以通过减小ω 的值，使其搜寻在小空间的范围内进行，以便更快找到最优解.

综上所述，惯性权重因子ω 应该随进化速度的降低而减小，随粒子聚集程度的增加而增大，这样式(6)可以进一步表示为

式中ωini为惯性权重的初始值，一般取ωini=1.

3 惩罚函数法求解算法

目前，对于优化问题的求解已经提出了很多方法，文中利用惩罚函数法将优化问题的约束条件进行处理来寻求最优选址结果. 对于带有约束条件的优化问题的一般形式可以描述为

由式(10)可以看出，目标函数存在着约束条件，并且其约束条件有可能是非线性的.所以在实现目标函数的求解过程中，在满足约束条件的前提下，需使求解的目标函数最小.这样，可以建立一个包含目标函数和约束条件的辅助函数，即惩罚函数

式中σ 为惩罚因子，一般选取一个很大的正数.

这样，对于x 在可行域内的点，惩罚项为0，则F(x，σ)=f(x)，对于可行域以外的x 点，惩罚项是一个极大的正数，由于问题是求解最小值，所以这些点就会在迭代过程中被舍弃.因此，惩罚项引入可以保证在求解过程中，迫使迭代点靠近可行域或者一直保持在可行域内移动，从而得到问题的结果.也就是说通过惩罚函数，对违反约束条件的点进行惩罚，使得在满足约束条件的前提下对目标函数寻优，其中惩罚因子σ 越大，惩罚的力度也就越大［7－10］.

综上所述，通过惩罚函数法处理的优化问题，实际是将有约束条件的目标函数转化成无约束条件的函数来进行最优化求解.

现根据光伏发电系统的控制室选址模型的目标函数和约束条件，通过上述构造惩罚函数的方法，转化为一个没有约束条件的辅助函数F(x，σ). 由于选址模型的目标函数没有等式约束条件，所以

这样式(12)就是一个带有惩罚项的没有约束条件的函数，再对其求解最小值即可得到最初所要搜寻优化问题的最佳结果.

4 算法实例

以某县所需建设的独立光伏电站为例，对其控制室选址进行优化设计. 该县光伏发电供电区域内各个负荷点的坐标以及用电量需求见表1.

表1 供电负荷点坐标和用电量

利用惩罚函数法将式(1)和式(2)进行处理，构造辅助函数

式中xi，yi和εi的值见表1.

这样控制室选址模型优化问题转化成无约束条件的辅助函数求解最小值的优化问题. 首先设置惯性权重的参数:置初始状态下h1=0，s1=0，ωini=1，这样ω1=ωini=1.分别设ωs=0.05 和ωh=0.5，然后按照一般原则，定义粒子的个数为n =20，维数为2，迭代次数bm=500，c1=c2=2.

按照算法流程在MATLAB 软件中进行编程，分别赋予惩罚因子σ 不同的数值，可以得到相应的控制室地理坐标值和优化目标函数结果，见表2.算法流程如图1所示.

表2 优化算法的结果值

续表

图1 改进PSO 算法的流程图

最后根据优化结果生成取不同惩罚因子σ 时供电负荷点与控制室之间距离的关系曲线，分别如图2—4 所示.

图2 σ=0 时控制室与各负荷点之间的距离

图3 σ=10 时控制室与各负荷点之间的距离

图4 σ=109 时控制室与各负荷点之间的距离

从上面3 个图中可以看出，选取σ=0 和σ=10时不满足不超过500 m 的选址条件.而σ=109时控制坐标(X9=353.929 2，Y9=491.309 1)到各负荷点的距离均小于供电半径R=500 m，而且目标函数的优化结果比惩罚因子σ 在其他取值时的优化结果都要小.所以，可以确定σ =109时对应控制室的坐标为其最优解.

通过对上述结果的分析可知，惩罚因子的选取对于实际问题的优化过程是有较大影响的，如果惩罚因子较小，惩罚力度不够，所惩罚函数的极小值点就远离约束优化问题的最优解，计算效率较低.

5 结 语

控制室的选址是光伏发电系统建设中非常重要的一个环节.文中基于改进的粒子群算法，利用惩罚函数法对控制室选址的数学模型进行优化，最后通过MATLAB 计算仿真.仿真结果表明，基于改进的粒子群算法在求解光伏发电控制室选址问题时可以得到最佳的选址结果，能够满足实际需要，其理论研究可为解决光伏发电系统建设中的相关问题提供依据.

［1］王平，周冲.基于粒子群算法的光伏电池MPPT 控制策略［J］.可再生能源，2013，31(5):26－28.

［2］王玺，周步祥.基于改进粒子群算法的风光互补发电系统经济运行研究［J］. 电源技术应用，2012(12):168－170.

［3］吴海涛，孙以泽，孟婥. 粒子群优化模糊控制器在光伏发电系统最大功率跟踪中的应用［J］.中国电机工程学报，2011，31(6):52－56.

［4］郑凌蔚，刘士荣，徐青鹤. 基于非线性扩散粒子群算法的光伏微网并网点恒定潮流控制［J］.电网技术，2010，34(10):152－155.

［5］张耀明.中国太阳能光伏发电产业的现状与前景［J］.能源研究与利用，2007(1):1－6.

［6］雷一，赵争鸣.大容量光伏发电关键技术与并网影响综述［J］.电力电子，2010(3):16－18.

［7］唐征岐，虞辉.太阳能光伏发电系统应用技术［J］.上海电力，2008(2):111－114.

［8］赵朝会.光伏发电技术的研究现状和应用前景［J］. 上海电机学院学报，2008，11(2):104－108.

［9］刘佳.含分布式电源的配电网保护技术研究［D］.郑州:华北水利水电大学，2013.

［10］姜彤，贾艳昌，刘怀强，等. 从投资和安全角度设计与优化淤地坝空间布局［J］.华北水利水电大学学报:自然科学版，2014，35(2):47－49.