粒子群优化自适应小波神经网络在带电局放信号识别中的应用
2014-11-25牛海清来立永沈杨杨
罗 新 牛海清 来立永 沈杨杨 吴 倩
(1.华南理工大学电力学院 广州 510641 2.广州供电局有限公司 广州 510620 3.南方电网超高压输电公司 广州 510620)
1 引言
局部放电(Partial Discharge,PD)在线检测中,各高压设备均处于带电运行状态,对电缆PD 信号的检测造成很大干扰,检测到的放电脉冲可能来自电缆本体、电缆终端头,也可能来自与其连接的其他设备(如开关柜等)。由于不同来源的PD 信号,对设备的危害不同,其判断标准也有所不同,所以对PD 信号的识别就显得尤为重要。
人工神经网络是由大量的功能和形式比较简单的神经元互相连接而构成的复杂网络系统,网络可以看作是从输入到输出的一个非线性映射。其作为一种成功的模式识别技术已在很多智能领域得到运用[1,2]。作为傅里叶变换的重要发展,小波变换不仅具有时-频窗口可自适应变化的特点,而且具有良好的局部化特性,已在PD 信号处理领域得到了广泛的应用[3-5,16,17]。如何将神经网络与小波变换的优势结合起来,一直是人们关注的问题[6-8]。传统的方法是用小波变换对信号进行预处理,即以小波空间作为模式识别的特征空间。文献[6]对不同故障工况下采集的故障电流信号进行多小波包分解,计算各频带的系数熵作为神经网络的输入进行识别取得了良好的效果。文献[7]利用小波变换提取出不同尺度下的能量特征作为神经网络的输入,成功对励磁涌流进行识别。但在这些应用中,小波变换与神经网络之间完全独立,并没有将二者有机的结合起来,小波参数一经给定就不做任何修正,即神经网络的输入是预先给定的时频特征。
Szu H 最早提出了自适应小波神经网络的概念,并将其应用在语音、声纳的识别中[9,10]。自适应小波神经网络在理论上将小波变换与神经网络进行了有机的结合,神经网络的隐含层传递函数由传统的Sigmoid 函数变为小波函数,小波的尺度因子与平移因子在神经网络的训练过程中自适应的调整,能够最大限度的对待分类信号进行特征提取[11-13]。文献[11]将自适应小波神经网络用于心电信号分类取得了良好的效果。文献[12]引入自适应小波神经网络对励磁涌流进行识别,识别率达到100%。但自适应小波神经网络在电气设备PD 识别中的应用却未见报到。本文引入自适应小波神经网络对XLPE 电缆在线检测中的检测到的PD 信号进行分类,并提出使用粒子群优化算法与BP 算法相结合对自适应小波神经网络进行训练。
2 局部放电试验
在配电电缆PD 在线检测中,电缆终端与开关柜相连接,所检测到的PD 脉冲信号可能来自电缆也可能来自开关柜。这些脉冲可以分为几种典型模式:电缆本体PD、电缆终端头PD、开关柜中的电晕放电、开关柜中的表面放电。英国HVPD 公司对不同来源的PD 信号进行了大量研究,获取了各种类型PD 的大量样本数据。各种典型的放电波形如图1所示,PD 检测时的采样频率为100MHz,每个波形的时域长度为1 500个采样点。
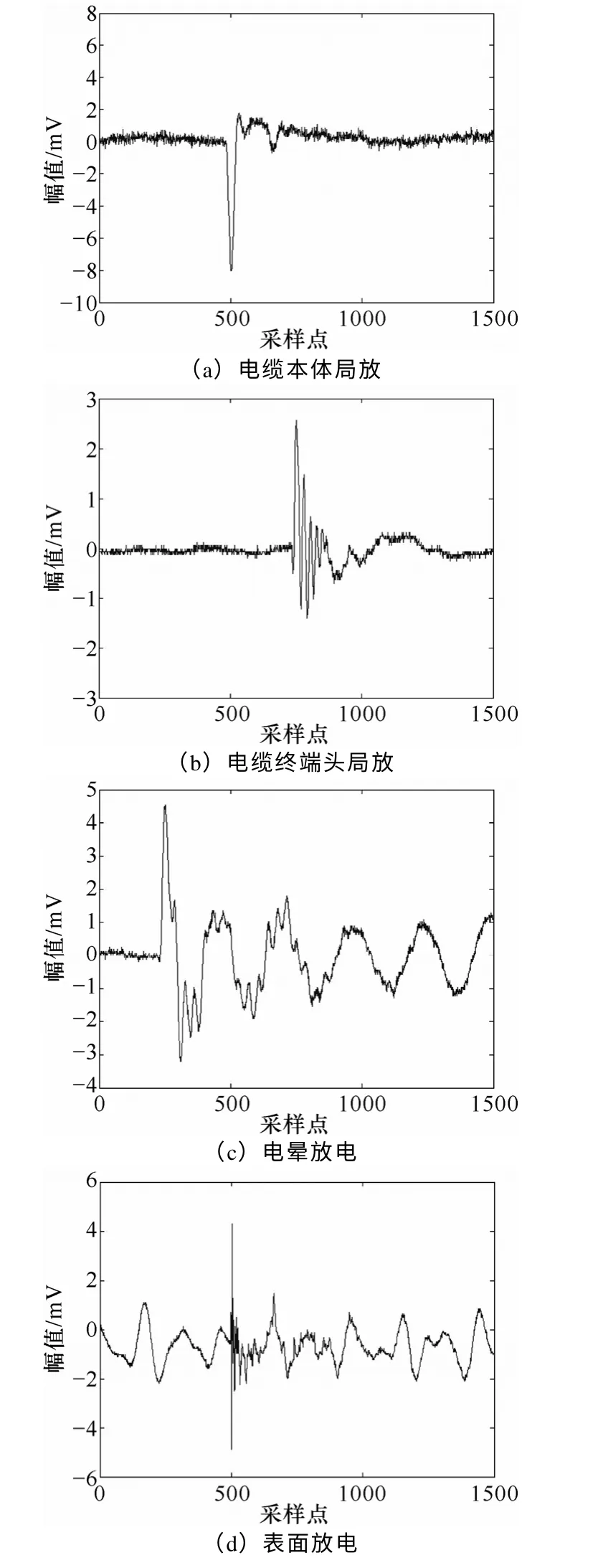
图1 各种典型放电波形Fig.1 Typical discharge waveforms
3 自适应小波神经网络模型
3.1 小波变换
在函数空间 L2(R)中,选择一个母小波函数ψ(x),使其满足约束条件
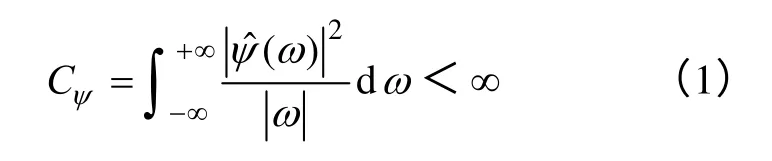
对 ψ(x)作伸缩、平移变换得到小波函数族{ψa,b(x)}。
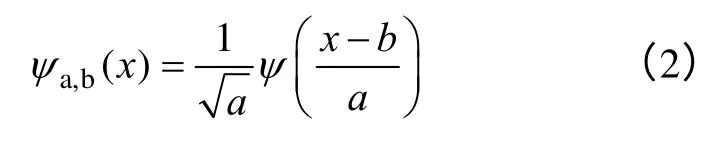
式中,a是尺度因子;b是平移因子。
对任意f(x)∈L2(R),其连续小波变换定义为
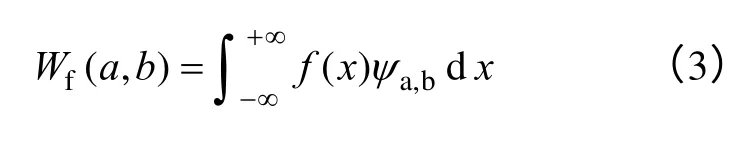
3.2 自适应小波神经网络
本文使用的模型是在Szu H 模型上的推广,即在输入和输出层之间加入一隐含层。这一结构能用于处理更为复杂的信号分类问题,收敛及泛化性能得到增强[12]。图2 给出了自适应神经网络结构图。
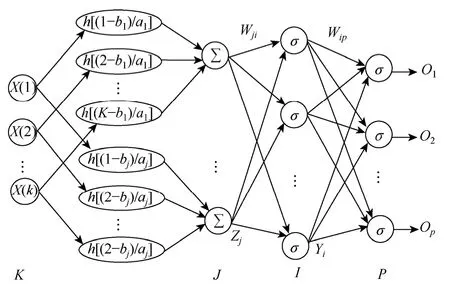
图2 自适应小波神经网络拓扑结构Fig.2 Structure of adaptive wavelet neural network
网络由两部分组成,第一部分为用于特征提取的小波层,第二部分是一个前馈神经网络,用于对信号的分类。其中x(k)为输入层第k个输入值,Zj为小波层第j个输出值,Yi为隐含层第i个输出值,Op为输出层第p个输出值,Wji为连接小波层节点j和隐含层节点i 的权重,Wip为连接隐含层节点i 和输出层节点p 的权重,aj和bj分别为小波层第j个节点的尺度因子和位移因子;K为输入层节点数,J为小波层节点数,I为隐含层节点数,P为输出层节点数。小波层采用母小波函数h(x),网络的输出层、隐含层传递函数均采用Sigmoid 函数σ(x)。网络输出O为
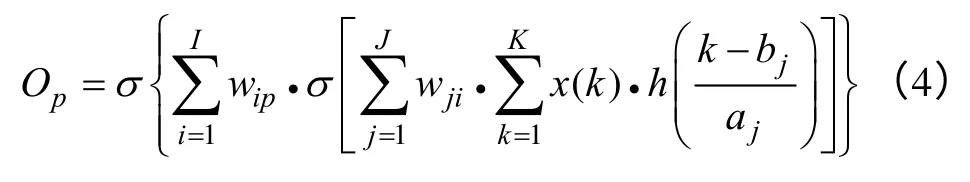
3.3 学习算法
传统的小波神经网络采用BP 学习算法,但BP算法在面对庞大网络及处理大样本数据时易出现陷入局部最小值,收敛速度慢甚至不收敛等问题。本文的研究对象为采集到的时域波形,其数据窗为1 500,即输入层有1 500个神经元,网络结构复杂,故不宜直接采用BP 算法。研究表明群智能算法对于保证收敛至全局最优有着良好的效果[13,14]。粒子群(Particle Swarm Optimization,PSO)算法是由Kennedy 和Eberhart 模仿鸟类集群飞行觅食提出的,PSO 算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解,群体中每个粒子的位置向量代表解空间的一组解向量,粒子在搜索空间以一定的速度飞行寻找最优解,飞行速度依据飞行经验动态调整。
PSO 算法首先初始化一群随机粒子(随机解)。假设d 维搜索空间中有m个粒子组成1个群体,第 i个粒子的位置(即解向量)和速度分别为Xi=(xi1,xi2,…,xid)和Vi=(vi1,vi2,… ,vid)。通过迭代来寻找最优解,在每一次迭代中,粒子通过跟踪2个最优解来更新自己:第1个是个体极值Qbset,即粒子本身所找到的最优解,另一个是全局极值Qgbest,即整个群体当前的最优解。本文选用PSO 算法与BP 算法相结合的方式对网络进行训练,具体步骤如下[15]:
(1)初始化粒子群,即为每一组连接权值、尺度因子、平移因子赋初值如式(5)。
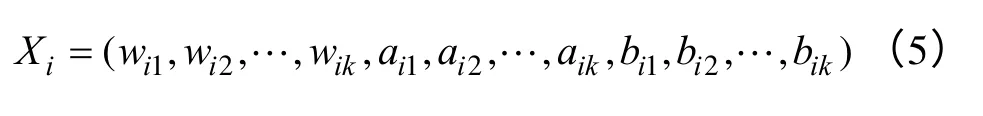
(2)将网络的输出误差定义为粒子的适应度函数如式(6)。计算各粒子的适应度
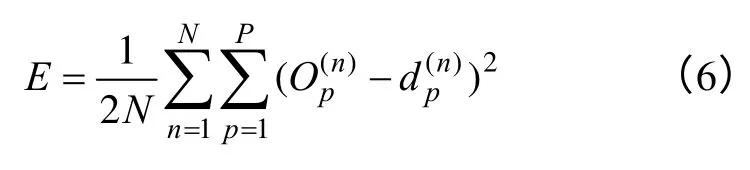
式中,N为样本数;P为输出维数;O为网络输出;d为目标输出。
(3)比较当前粒子的适应度与先前的最佳适应度,将二者中的较小值设为当前粒子的局部极值。
(4)选择所有粒子适应度中最好的一个,作为全局极值。
(5)按式(7)更新粒子速度。
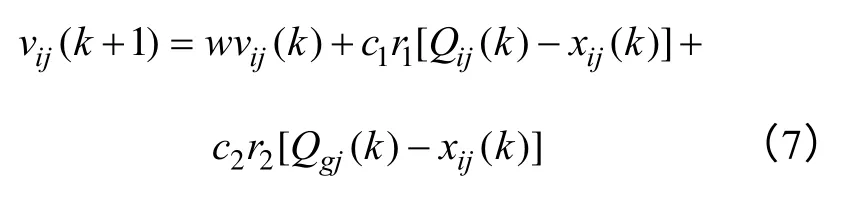
式中,w为惯性因子,它使粒子保持运动惯性;c1、c2为加速因子;r1、r2为两随机数,取值区间为[0 1];vij∈[-vmax,vmax]为第i个粒子第j 维空间的速度,vmax为允许移动的最大速度;xij∈[-xmax,xmax]为第i个粒子第j 维空间的位置,xmax为允许的最大空间位置;Qij为第i个粒子第j 维空间的局部极值,Qgj为第j为空间的全局极值。
(6)按式(8)更新粒子的位置。
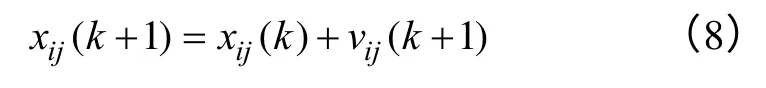
(7)如果算法满足误差精度或达到最大迭代次数,则退出PSO 算法,否则返回步骤(2)。
(8)将PSO 算法得到的各权值、尺度因子、平移因子作为初值,继续使用BP 算法进行二次优化,由于PSO 训练已接近全局最优,此处BP 算法学习效率应尽可能小。若训练结果优于PSO 训练结果,则输出BP 训练的网络,否则输出 PSO 训练的网络。基于BP 算法的自适应小波神经网络的各权值及小波参数的修正值为
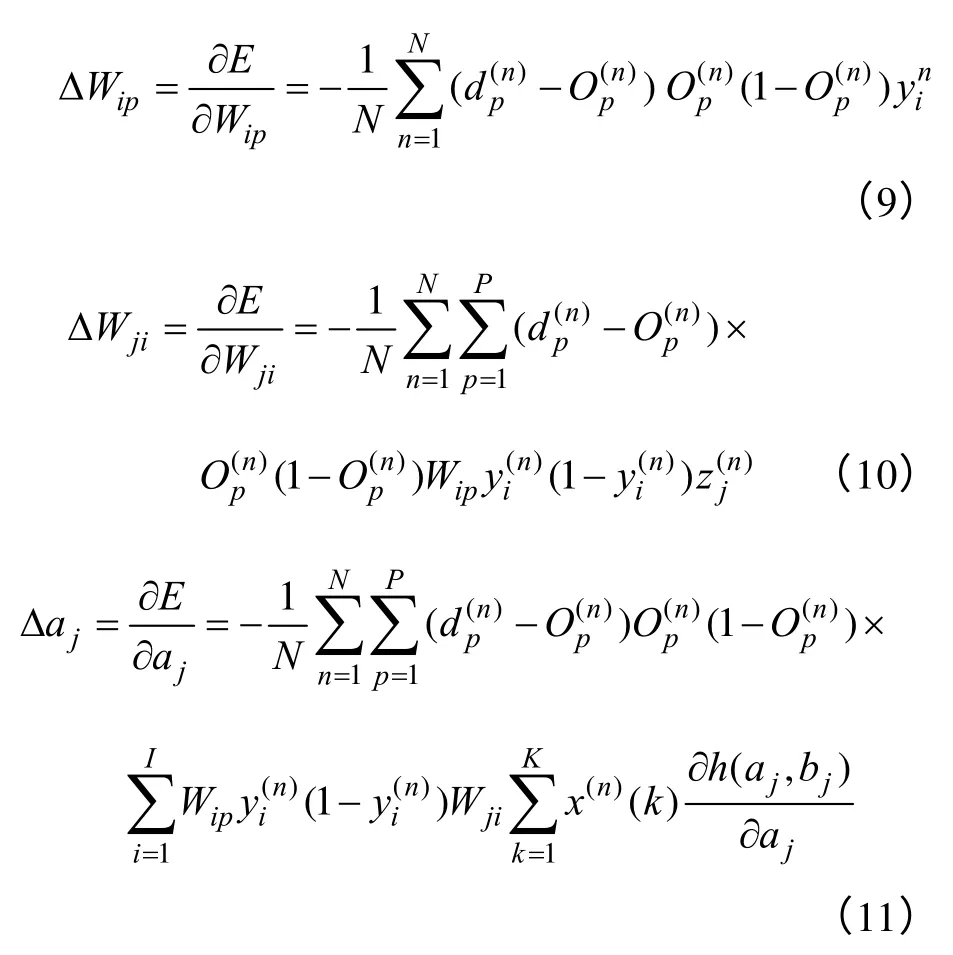
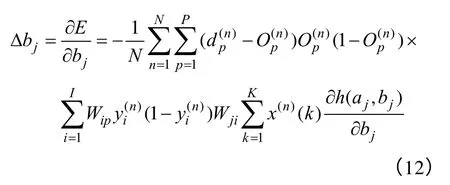
4 网络的构建
网络的待识别对象为采集到的时域波形,每个波形15μs,采样频率为100MHz,即数据窗长度为1 500,由此确定网络的输入神经元个数为1 500。网络的输出为4 种待识别信号的编码,电缆本体局放、电缆终端头局放、表面放电、电晕放电分别对应00,01,10,11。故网络的输出神经元个数确定为2。
小波神经网络小波层及隐层的确定是使用网络的关键,包括小波函数的选取、小波层神经元个数及隐层神经元个数的确定以及小波参数的初始化。
小波函数的性质往往是相互制约的,不可能同时达到最佳,而利用自适应小波神经网络对PD 信号进行识别,实质上是通过尺度和位移因子的自适应选取,来寻找一组最适合表征待分类信号特征的小波。故对于小波函数的特性并没有严格要求,但小波函数必须有时域解析式[12,13,16]。Morlet 小波具有良好的时频局部化特性,时域解析式简洁,本文选择中心频率为10rad 的Morlet 小波作为自适应小波神经网络的母小波,式(13)为Morlet 小波对应的小波族。
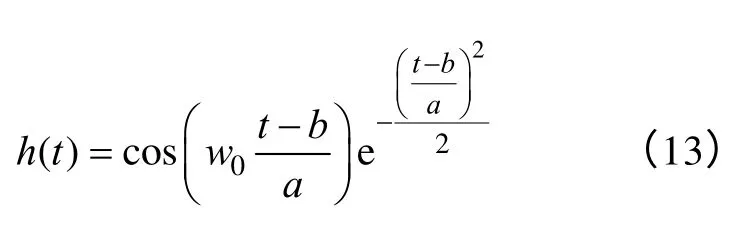
图3为中心频率 w0=10 时Morlet 小波的时域波形。小波层神经元个数与所选择的小波函数及待分类信号的时频特性有关,一个小波层神经元个数对应一个时频窗,选择小波层神经元个数的实质就是要用多少个时频窗能够最大限度的表征PD 信号的特征。个数过少无法充分表征信号,过多则造成信息冗余影响网络的泛化性能。本文采用的方法是试错法,即先用样本数据对网络进行训练,再采用检验样本对训练好的网络的泛化能力进行检验以确定小波层神经元数。经反复调试本文选择小波层神经元个数为20。关于隐层神经元个数的确定,文献[11]指出当隐层神经元个数等于小波层神经元个数时,网络的分类效果最好,故本文选择隐层神经元个数为20。至此确定的自适应小波神经网络的结构为1 500-20-20-2。
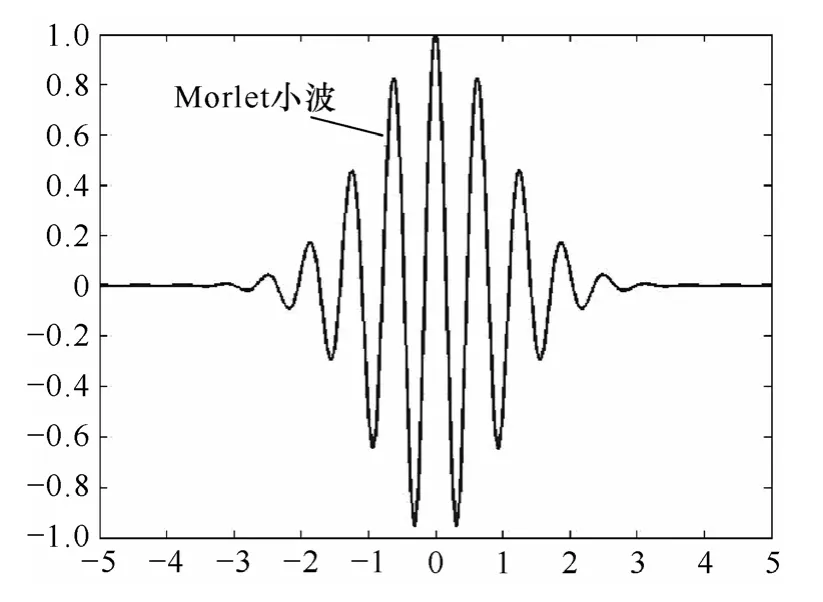
图3 Morlet 小波时域波形Fig.3 Morlet wavelet in time domain
虽然网络的参数在训练过程中会自适应的调整,但网络参数的初始值对于网络的收敛速度有着很大的影响。由奈奎斯特采样定理知,要使幅频响应不出现混迭现象必须满足
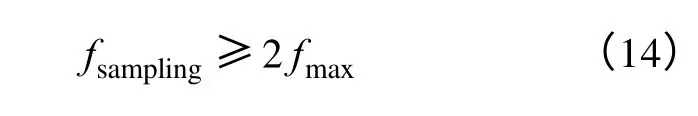
式中,fsampling为采样频率,Morlet 小波的采样频率等效于 1Hz;fmax为小波函数的最高频率,Morlet小波可取则由式(14)可得a≥2.5。当数据窗长度给定时(本文为1 500),a 与数据窗长度又有如下关系

式中,K为数据窗长度,Δt为Morlet 小波的时窗宽度,本文取8,得到a≤187.375。故对a 的初始化即生成一组2.5 至187.375 之间的随机数。
平移因子b 按式(16)选取。

式中,J为小波层神经元个数。连接权值的初始值为一组0 至1 之间的随机数。
5 样本处理
5.1 波形去噪
在线检测中,各高压设备均处于带电运行状态,对电缆PD 信号造成很大干扰,因此去噪是特征提取的首要任务。本文使用波形数据的噪声干扰主要是白噪声,利用小波包降噪的算法流程如图4 所示。小波包变换可以将原始信号分解为一系列近似分量和细节分量,白噪声信号集中表现在细节分量上。使用一定的阈值处理细节分量,即将小于阈值的小波系数置0,再经小波包重构即可以得到平滑的信号。

图4 小波包去噪流程Fig.4 Denoising process using wavelet packet
显然,阈值的选择关系到整体去噪的效果。Daubechies 系列小波正交、紧支撑,对不规则信号敏感,故本文选用db4 小波进行小波变换。利用db4小波对长度为1 500个采样点的波形进行4 层小波分解,先对各类信号进行默认阈值去噪,重构信号,再根据去噪效果调整阈值,反复操作直至去噪效果满意为止。图5为一个典型电缆本体PD 信号的去噪效果。更详细的说明及研究将另文撰写。
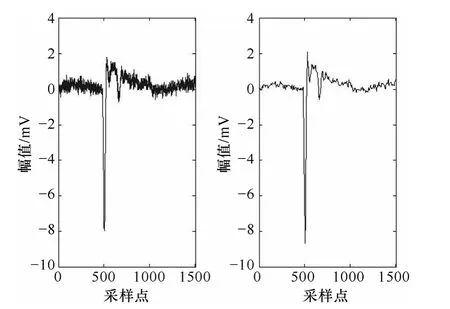
图5 去噪效果Fig.5 Denosing results
经去噪处理后,重构百分比(即处理后信号剩余的能量百分比)为97.2%;零系数所占比例为85.5%。由图可见重构波形与原始波形基本相似,保留了绝大部分信息,对白噪声起到了很好的抑制作用。
5.2 数据归一化
不同类型PD 信号的峰值不同,对同一类型的PD,考虑到放电的分散性,PD 峰值也会有波动。为使得样本数据更适合于神经网络处理,必须对PD以峰值为基准进行归一化处理。这种归一化可分为全局归一化和内部归一化。全局归一化是以测得的全部PD 信号中的最大峰值为基准。这种方法的优点是将所有PD 信号在同一尺度下比较,相异性明显,利于识别,但缺点是小信号会被“淹没”并且同一类型的PD 信号由于分散性也可能被判断为不同类型的PD;内部归一化是以各个PD 信号本身的峰值为基准进行数据归一化,它克服了全局归一化的缺点,但也可能削弱不同类型PD 之间的相异性。本文采用内部归一化处理,如式(17)。
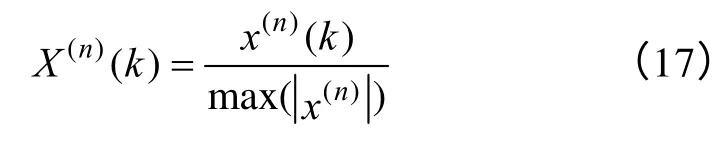
式中,X(k)为归一化之后的第k个采样值。
6 试验结果
本文使用HVPD 公司试验获得的4 种典型放电的波形数据各50 组作为样本,从样本中各随机挑选25 组共100 组作为训练样本,另外100 组作为检验样本。对样本进行去噪及归一化之后,使用训练样本对自适应小波神经网络进行训练。误差精度定为0.01,PSO 算法迭代次数定为500。网络训练误差曲线如图6 中实线所示。
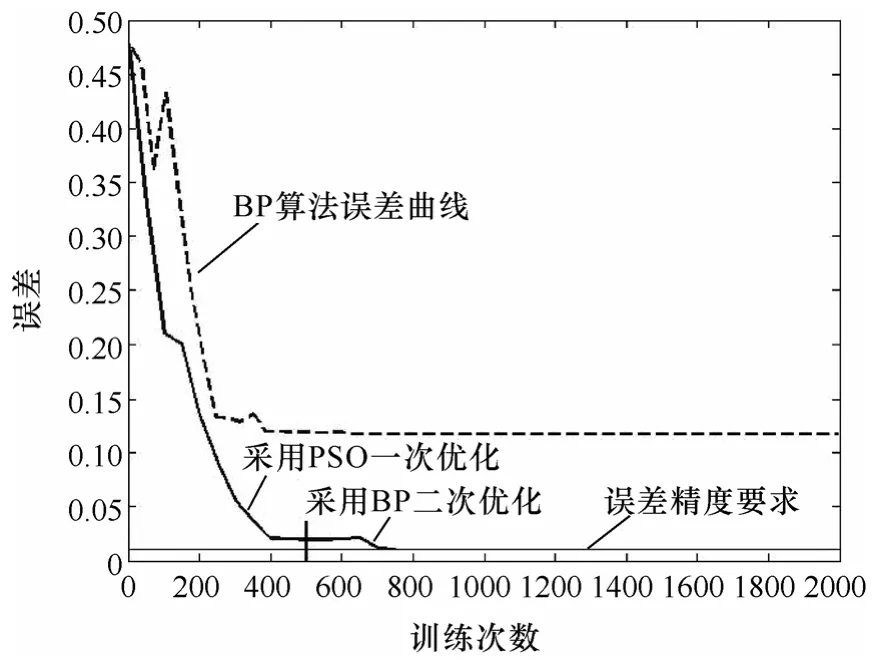
图6 学习过程误差曲线Fig.6 Errors during learning process
使用PSO 算法对网络参数进行一次优化后网络误差达到0.019 5,再使用BP 算法对参数进行二次优化。由于BP 算法仅作为二次优化,此处使用小学习效率,设为0.01。训练756次后误差达到目标精度。图6 中虚线为网络参数采用相同初值,单独使用BP 算法对网络进行训练的误差曲线,训练2 000次后仍无法达到目标精度。比较可见,PSO 与BP 算法结合对自适应神经网络进行训练,训练效果要优于单独使用BP 算法。使用检验样本对网络进行检验,网络的输出可以看成是某类PD 的隶属度,即带有模糊评判性质,与人的思维习惯相符。对输出做四舍五入处理,识别效果如表1 所示。由表1可知,使用自适应小波神经网络对各种类型的PD信号进行识别是可行的,使用PSO 与BP 结合算法训练网络,网络的识别率达到100%。
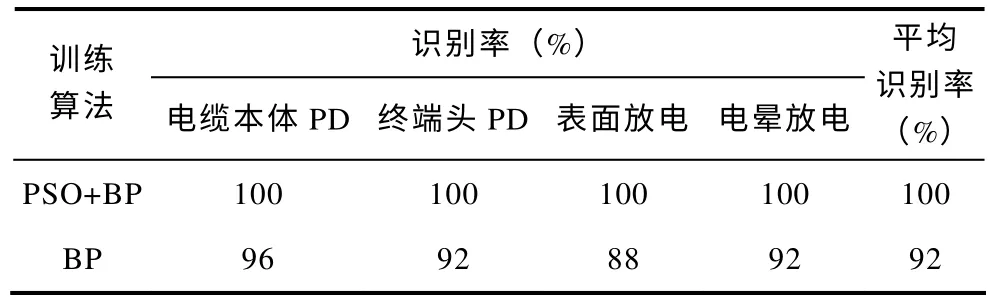
表1 自适应小波神经网络识别效果Tab.1 Recognition rate of adaptive WNN
为进一步比较网络结构不同对网络性能的影响,笔者改变网络小波层及隐含层神经元个数,同样使用PSO 与BP 结合算法对网络进行训练,PSO 训练次数定为500,总最大训练次数为1 000。使用检验样本进行检验,网络识别效果如表2 所示。
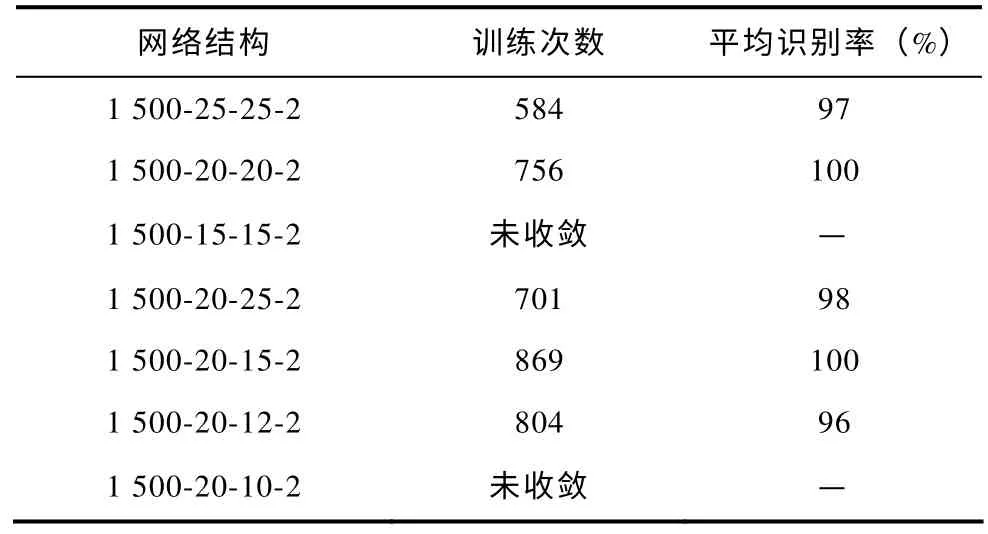
表2 不同结构网络识别效果比较Tab.2 Comparison of adaptive WNN with different structures
小波层神经元个数为20 时,能够充分提取信号特征,网络的泛化性能最好。改变隐含层神经元的个数,当隐层神经元个数为25,20,15 时均能很好的对PD 信号进行识别,当隐层神经元个数降为12 时,识别率为96%,泛化性能开始下降,可见小波神经网络的隐含层神经元个数接近小波层神经元个数时网络性能最优,与文献[11]中结论一致。
讨论采用不同小波函数时对网络性能的影响。常用具有时域解析式的小波函数除Morlet 小波外,还有Marr 小波以及Shannon 小波,其时域波形如图7 所示。
图7 常用小波函数Fig.7 Wavelet function used commonly
网络结构选择1 500-20-20-2,使用相同的初值对采用三种不同小波的自适应神经网络进行训练,使用检验样本对网络进行检验,网络识别效果如表3 所示。可以看出,小波层使用Morlet,Marr 及Shannon 小波函数都能很好地对PD 信号进行特征提取,最终的识别率都在95%以上。使用Marr 小波及Shannon 小波在收敛速度上要明显优于Morlet小波,但识别率略有下降。在实际应用中可根据具体需要选择不同的小波函数。

表3 不同小波函数识别效果比较Tab.3 Comparision of adaptive WNN with different wavelet function
7 结论
本文引入自适应小波神经网络对XLPE 电缆在线检测中的4 种PD 信号进行识别,使用PSO 算法与BP 算法相结合对网络进行训练,得到以下结论:
(1)采用PSO 与BP 结合算法对网络进行训练,训练效果明显优于单独使用BP 算法对网络进行训练。前者在训练756次后达到目标精度,识别率达到100%。后者训练2 000次尚未收敛。
(2)对于本文待分类的PD 信号,小波层神经元个数取20 能够充分对信号进行特征提取,且不影响网络的泛化性能。隐层神经元个数接近小波层神经元个数时,网络的性能最优。
(3)比较了小波层采用不同小波函数时网络的性能。使用Marr 小波及Shannon 小波在收敛速度上要优于使用Morlet 小波,但识别率略有下降。实际应用中可根据具体需要选择不同的小波函数。
[1]淡文刚,陈祥训,郑健超.采用小波分析与神经网络技术的局部放电统计识别方法[J].中国电机工程学报,2002,22(9):1-5.Dan Wengang,Chen Xiangxun,Zheng Jianchao.Classification of partial discharge distribution using wavelet transform and neural network[J].Proceedings of the CSEE,2002,22(9):1-5.
[2]姜磊,朱德恒,李福祺,等.基于人工神经网络的变压器绝缘模型放电识别的研究[J].中国电机工程学报,2001,21(1):21-24.Jiang Lei,Zhu Deheng,Li Fuqi,et al.ANN based discharge pattern recognition of insulation models of electrical transformers[J].Proceedings of the CSEE,2001,21(1):21-24.
[3]何正友,蔡玉梅,钱清泉.小波熵理论及其在电力系统故障检测中的应用[J].中国电机工程学报,2005,25(5):38-43.He Zhengyou,Cai Yumei,Qian Qingquan.A study of wavelet entropy theory and its application in electric power system fault detection[J].Proceedings of the CSE,2005,25(5):38-43.
[4]钱勇,黄成军,陈陈,等.多小波消噪算法在局部放电检测中的应用[J].中国电机工程学报,2007,27(6):89-95.Qian Yong,Huang Chengjun,Chen Chen,et al.Application of multiwavelet based on denoising algorithm in partial discharge detection[J].Proceedings of the CSEE,2007,27(6):89-95.
[5]张静远,张冰,蒋兴舟.基于小波变换的特征提取方法分析[J].信号处理,2000,16(2):156-162.Zhang Jingyuan,Zhang Bing,Jiang Xingzhou.Analyses of feature extraction methods based on wavelet transform[J].Signal Processing,2000,16(2):156-162.
[6]李东敏,刘志刚,蔡军,等.基于多小波包系数熵和人工神经网络的输电线路故障类型识别方法[J].电网技术,2008,32(24):65-69.Li Dongmin,Liu Zhigang,Cai Jun,et al.Transmission lines fault recognition method based on multi-wavelet packet coefficient entropy and artificial neural network[J].Power System Technology,2008,32(24):65-69.
[7]Mao P L,Aggarwal R K.A novel approach to the classification of the transient phenomena in power transformer using combined wavelet transform and neural network[J].IEEE Transactions on Power Delivery,2001,16(4):654-660.
[8]张举,王兴国,李志雷.小波包能量熵神经网络在电力系统故障诊断中的应用[J].电网技术,2006,30(5):72-76.Zhang Ju,Wang Xingguo,Li Zhilei.Application of neural network based on wavelet packet-energy entropy in power system fault diagnosis[J].Power System Technology,2006,30(5):72-76.
[9]Szu H H,Telfer B,Kadambe S.Neural network adaptive wavelets for signal representation and classification[J].Opt.Eng.,1992,31(9):1907-1916.
[10]Telfer B A,Szu H H,Dobeck G J,et al.Adaptive wavelet classification of acoustic backscatter and imagery[J].Optical Engineering,1994,33(7):2190-2203.
[11]刘春玲,王旭.基于改进的自适应小波神经网络的心电信号分类[J].系统仿真学报,2007,19(14):3281-3284.Liu Chunling,Wang Xu.New adaptive wavelet neural network for ECG recognition[J].Journal of System Simulation,2007,19(14):3281-3284.
[12]李海锋.王钢.李晓华,等.电力变压器励磁涌流判别的自适应小波神经网络方法[J].中国电机工程学报,2005,25(7):144-150.Li Haifeng,Wang Gang,Li Xiaohua,et al.Distinguish between inrush and internal fault of transformer based on adaptive wavelet neural network[J].Proceedings of the CSEE,2005,25(7):144-150.
[13]阳国庆 郑殿春 孙学勇.基于小波神经网络局部放电模式识别方法的实验研究[J].哈尔滨理工大学学报,2005,10(5):98-101.Yang Guoqing,Zheng Dianchun,Sun Xueyong.An experiment study of partial discharge pattern recognition method based on wavelet neural networks[J].Journal of Harbin University of Science and Technology,2005,10(5):98-101.
[14]Lahiri S K,Ghanta K C.Development of a hybrid artificial neural network and genetic algorithm model for regime identification of slurry transport in pipelines[J].Chemical Product and Process Modeling,2009,4(1):1-32.
[15]马修元,段钰锋,刘猛,等.基于PSO-BP 神经网络的水焦浆管道压降预测[J].中国电机工程学报,2012,32(5):54-60.Ma Xiuyuan,Duan Yufeng,Liu Meng,et al.Prediction of pressure drop of coke water slurry flowing in pipeline by PSO-BP neural network[J].Proceedings of the CSEE,2012,32(5):54-60.
[16]徐长发,李国宽.实用小波方法[M].武汉:华中科技大学出版社,2001.
[17]周力行.变压器局部放电检测中的小波包去噪算法[J].高电压技术,2001,27(1):19-21.Zhou Lixing.Wavelet packet de-noising arithmetic in PD detecting transformer[J].High Voltage Engineering,2001,27(1):19-21.
