变速风力发电系统统一功率控制策略研究

陈 杰 陈家伟 龚春英

（南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016）

1 引言

考虑到中小型风力发电机组功率等级较低（一般在100kW 以下），其通常采用定桨距永磁直驱结构并以变速方式运行以提高机组发电效率和降低成本[1,2]。为此，本文将变速定桨永磁直驱风力发电机组作为研究对象。

为提高机组捕获到的风能，需要在全风速范围内对机组实施功率优化控制，即控制机组按图1 中所示的最佳功率曲线运行[3]。主要包含三部分：低风速区的最大功率跟踪（MPPT）运行以及高风速区的限转速和限功率运行。

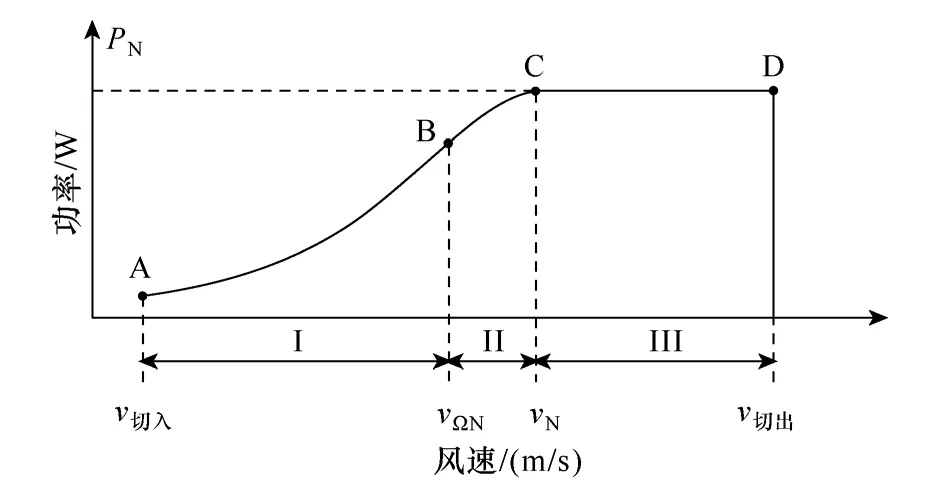
图1 理想运行曲线Fig.1 Ideal operation curve

对于低风速区的最大功率跟踪控制运行，目前已有的MPPT 控制策略主要分为三类：①最佳叶尖速比法；②扰动观察法（爬山法）；③基于最佳关系曲线的功率反馈法。最佳叶尖速比法通过测量风速和机组的转速信号，直接将机组运行的叶尖速比控制在最佳位置，从而实现机组的MPPT 运行[4]。然而，该方法因需测量风速，控制精度低，成本高，较少采用[5]。爬山法通过扰动机组的转速，观察由此引起的功率变化从而控制机组向最大功率点方向靠近[6,7]。该方法不需测量风速且不需预知机组的气动特性曲线，具有成本低和通用性强等特点。但该方法也存在两个主要缺点：一是运行中始终存在功率脉动，增加了传动链载荷；二是对转动惯量较大的机组，跟踪速度慢，且在风速变化较快时易出现跟踪失败现象。因此，该方法适合用于转动惯量较小的小功率（几百瓦到几千瓦）机组。对于转动惯量较大的中等功率（几十千瓦及以上）机组，具有较快跟踪速度的功率反馈MPPT 控制方法则更为适用[8-10]。但该方法需预知风力机的气动特性曲线，通用性差。

此外，机组在高风速区运行时，为保证机组的安全运行，需对机组的转速和功率进行限制。因定桨距机组桨距角固定不可调节，机组在高风速区的恒功率控制相比变桨距机组困难。目前国内外对变速定桨机组在高风速区的功率限制控制策略的相关报道较少。文献[11]提出在高风速区采用恒转速失速方法来限制机组的输出功率，一方面实现了对机组在高风速区运行转速的限制；另一方面因转速恒定，风速增加时风能利用系数下降，达到了减小机组捕获能量的作用。然而，随着风速增大，机组的输出功率仍将继续增大，发电机和变换器的容量需随之增大。文献[12]提出一种高风速区的恒输出功率失速控制策略，指出在额定风速以上通过增大机组的输出功率，迫使机组进入失速区运行，以减小机组捕获的功率。然而，考虑到该方法中又希望输出功率被控制为恒定输出，即实现恒输出功率运行，因此该控制策略存在严重的稳定性问题。为保证机组运行稳定，需要在控制环路中引入时间常数大于机组转动惯量的低通滤波器，这严重影响了机组在额定风速以下MPPT 运行速度。

综上所述，本文首先在低风速区将爬山法和功率反馈MPPT 方法相结合，提出一种改进型MPPT控制策略。该策略首先运用爬山法寻求到机组的最大功率运行点。一旦控制策略寻求到一个最佳功率点，控制系统将转入功率反馈MPPT 控制模式以提高机组的跟踪速度，并消除爬山法跟踪过程中的功率脉动。所提出的方法不需要预知风力机的气动特性，具有很好的通用性。之后，为在全风速运行范围内对机组实施功率优化控制，本文在所提出的改进型 MPPT 控制策略基础上引入气动功率控制外环，当机组功率超过额定功率后，通过功率外环的作用降低机组运行的转速，迫使机组进入失速区运行，从而实现了对机组在高风速区的恒功率运行控制。此外，本文提出方法可实现无传感器（风速和转速传感器）控制，大大降低了系统成本。最后，为验证本文提出控制策略的正确性，将所提出的方法运用到不同风力发电系统中进行实验研究，结果验证了所提出方法的正确性和可行性。

2 系统结构及统一功率控制策略

本文研究的变速定桨风力发电系统具有如图2所示的结构。定桨距风轮与永磁同步发电机采用刚性连接方式。发电机输出的三相交流电经过二极管整流后变为直流电，通过Boost 变换器升压后接入直流母线。机组按是否接入电网可分为并网或离网形式。然而，采用不同形式的接法时机组的直流母线电压Vl通常都被控制为恒定值，可等效为一个电压源，并网的功率（蓄电池充电功率）则通过控制并网电流（充电电流）进行控制。因此，机组结构形式对系统功率控制策略无影响，均通过控制Boost变换器实现。本文采用离网风力发电系统结构。图2 还给出了本文提出的统一功率控制策略原理框图，主要由改进的MPPT 控制策略、转速环调节器（PI）以及恒功率环调节器（PI1）组成。下面对统一功率控制策略的运行机理进行详细分析。

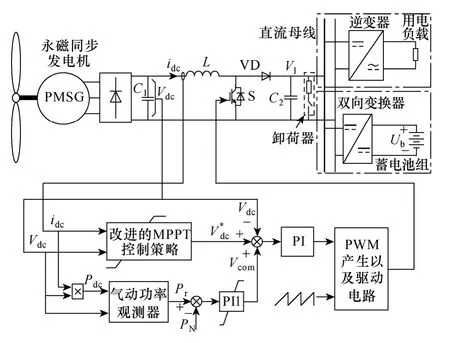
图2 所研究的机组结构形式和提出控制策略框图Fig.2 Turbine structure under consideration and the block diagram of the proposed control strategy

3 控制策略工作原理分析

3.1 最佳MPPT 控制关系导出

由空气动力学原理可知，定桨距风力机捕获的气动功率可表示为

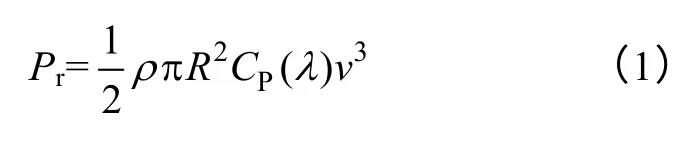
式中，Pr为气动功率；ρ为空气密度；v为风速；R为风轮旋转平面半径；CP为风力机的风能利用系数，对于定桨距机组，其值仅为叶尖速比λ 的函数，且λ 可表示为机组转速ω 和风速v 的关系

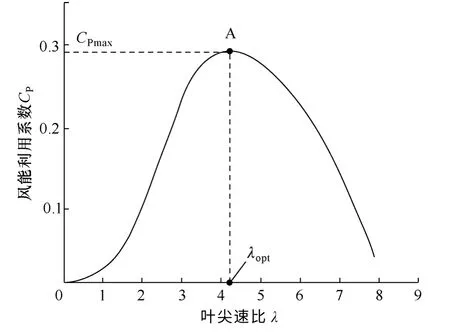
图3 1.2kW 风力机CP-λ 曲线Fig.3 CP-λ curve of a 1.2kW wind turbine

图3 所示为一台额定功率为1.2kW 的定桨距风轮的CP-λ 曲线。若能控制机组的转速时刻跟随风速变化，使机组始终工作在最佳叶尖速比λopt，可使机组捕获最大的功率系数CPmax，此时机组运行于最佳运行功率Prmax处

式中，ωopt为最佳转速；kopt为最佳功率系数，且有

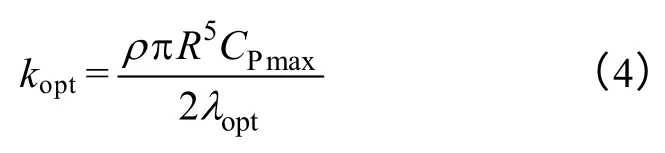
对于永磁同步发电机，其产生的反电动势E满足

式中，Ke为电动势系数；Ф为永磁磁通。由此可得电机输出相电压V

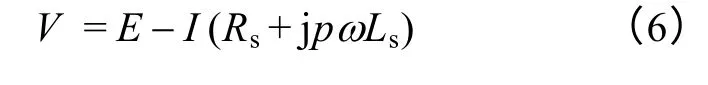
式中，I为相电流；Rs为相绕组电阻；p为极对数；Ls为定子电感。

当电机输出采用二极管整流时，整流后的电压（即图2 中直流侧电压）Vdc可表示为

由式（5）～式（7）可得

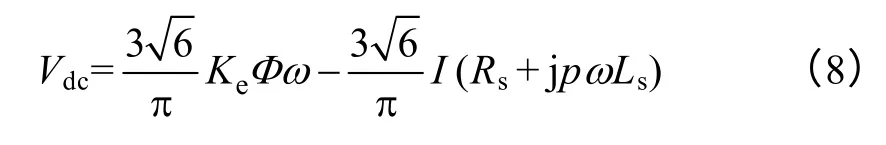
由式（8）可知，因电机相绕组电阻Rs和定子电感Ls的影响，永磁同步电机输出直流侧电压Vdc与转速ω 呈非线性关系。然而，对于采用永磁同步发电机的中小功率风力发电机组，为简化机组功率控制，可对电机的整流电压Vdc与其转速ω 之间的关系进行线性化近似，从而实现机组的无转速传感器控制[13]。本文中采用的线性化近似方法为使线性化后的Vdc-ω 曲线更加接近机组在高风速（也即高转速）运行时Vdc-ω 的关系曲线。这样虽然在风速较低时会因Vdc-ω 关系的近似偏差使机组无法运行于最大功率点，但由于此时机组发出功率较小，机组长期运行时因近似而产生的低风速区的功率丢失所占比例较小。近似后Vdc与ω 呈线性关系为

式中，kv为电压转速系数。

注意到机组运行于最大点时有

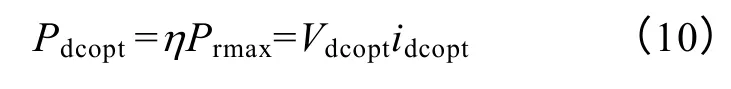
式中，Pdcopt、Vdcopt与idcopt分别为机组最大功率运行时的输出功率、直流侧电压和直流侧电流；η为机组效率。因此，联立式（3）、式（9）与式（10）可知，机组运行于最大功率点时直流侧电压和电流满足关系

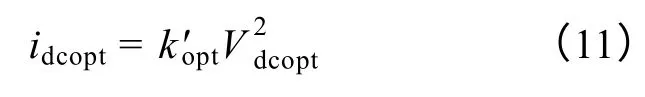
式（11）为本文所采用的实现MPPT 策略的最佳关系。由该式可知，只要能在任意风速下得到机组的一个最大功率跟踪运行点（Vdcopt，idcopt），则可计算出最佳关系系数。之后，可基于所得的最佳关系，通过检测直流侧的电压和电流信号实现机组在额定风速以下的MPPT 控制。综上，本文提出的MPPT 策略实现可分为两个步骤：①采用扰动观察法找到机组的最佳关系系数（定义为训练模式）；②运用式（11）对机组实施基于最佳关系曲线的MPPT 控制（定义为应用模式）。

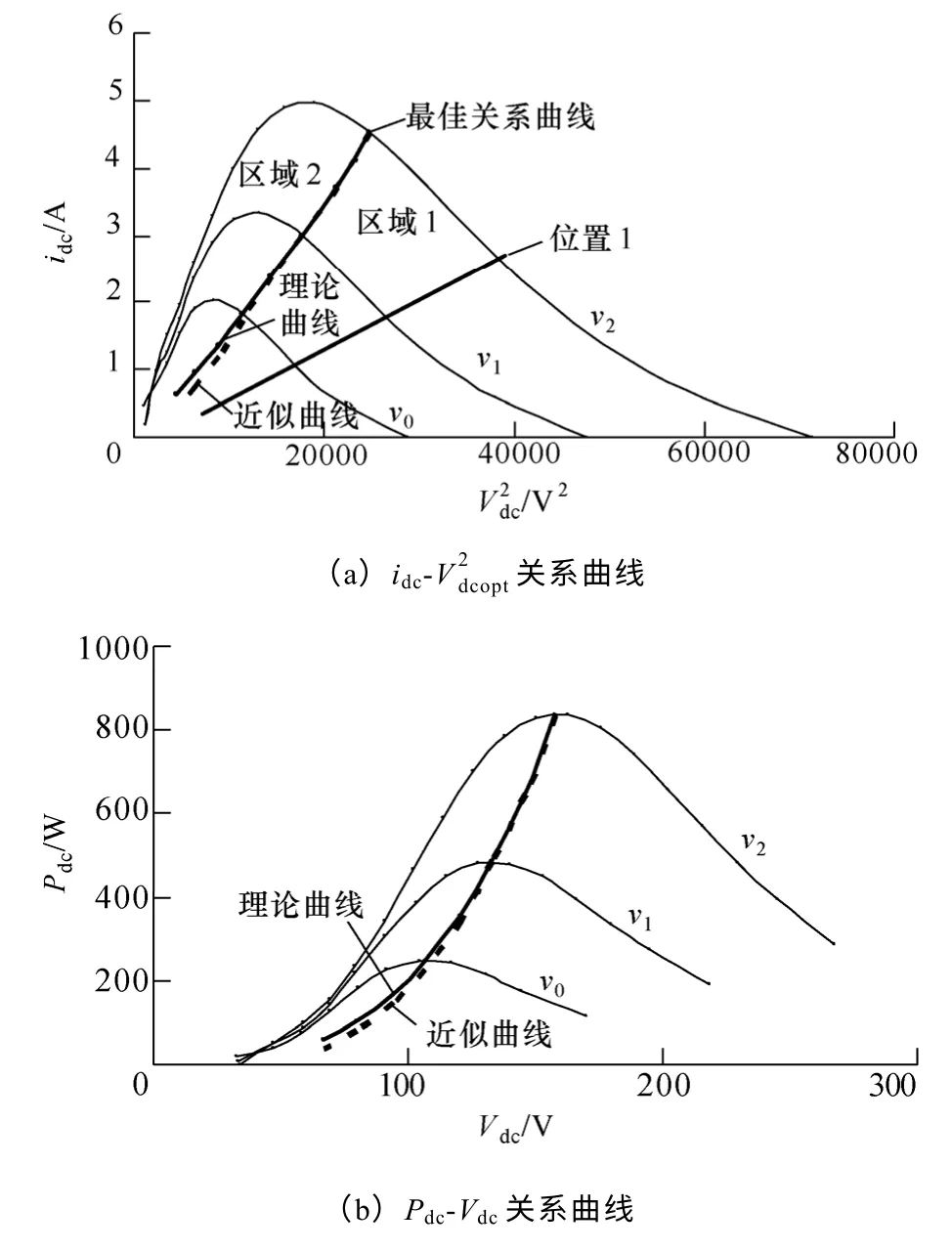
图4 所用风力机CP-λ 曲线Fig.4 CP-λ curve of the adopted wind turbine

此外，考虑到式（11）所示结论是在直流侧电压与电机转速近似呈线性关系的条件下推导得出的。图4 给出了具有图3 所示气动特性曲线的风力机在不同风速下近似最佳关系曲线与理论曲线的对比图。从图4a 可看出，本文采用的近似关系只在较低风速区与理论曲线出现较小偏差。而由图4b 可知，因机组在低风速区运行时功率较小，本文因近似而产生的功率丢失甚小，可忽略不计。因此，本文采用的近似关系具有较好的精度，可用于对机组进行MPPT 控制。

3.2 统一MPPT 控制策略的实现

由图4b 可知，机组输出功率也具有单峰特性，据此可得

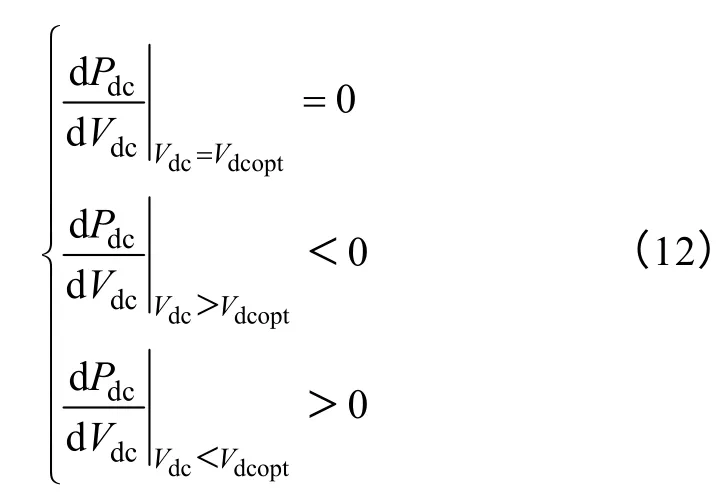
式中，Pdc为机组输出功率。

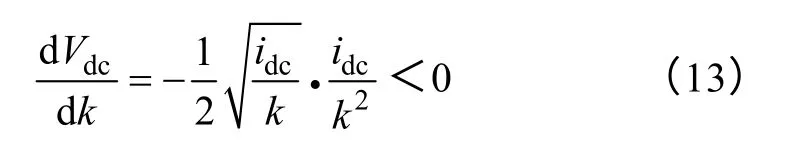
联立式（12）和式（13）可得

且满足关系

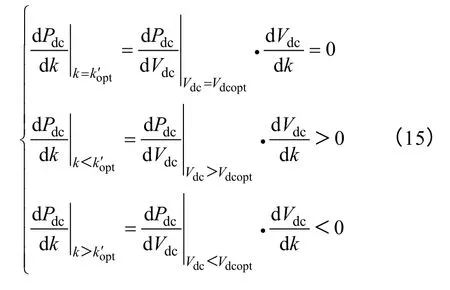
由式（15）可知，Pdc(k)也呈现单峰值特性，因此，可通过扰动关系k 实现机组的MPPT 运行。且一旦找到一个最大功率运行点，即，则MPPT 模式转为基于最佳关系的应用模式。图5 所示为改进型MPPT 控制训练模式和应用模式实现的原理框图。图6 所示为MPPT 策略的流程图，图5所示的MPPT 实现的最佳关系即由图6 所示方法寻求得出。

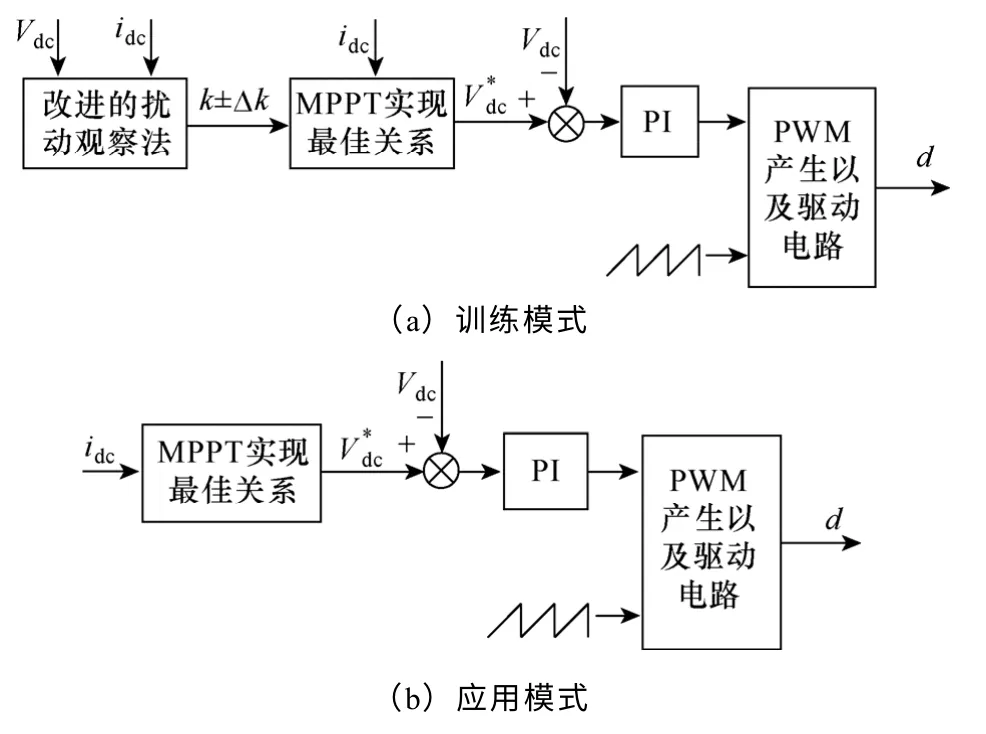
图5 MPPT 控制策略原理框图Fig.5 Block diagram of the proposed MPPT strategy

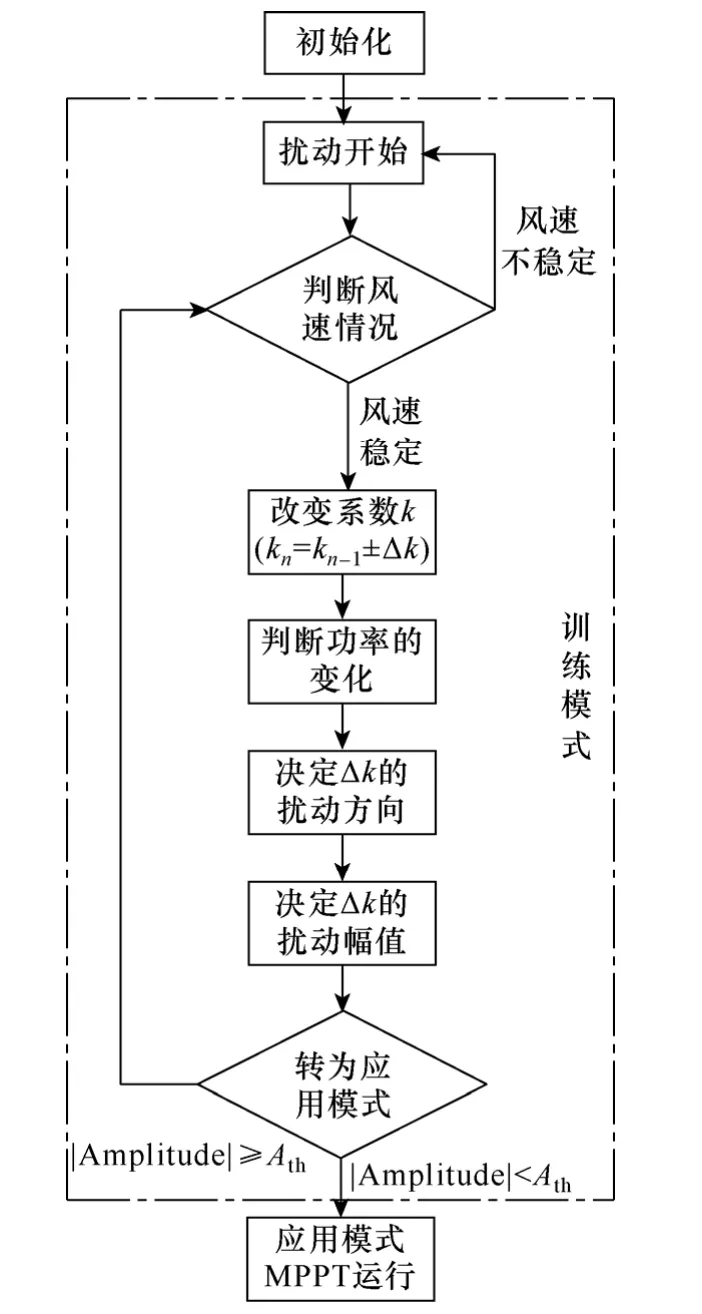
图6 改进MPPT 策略控制流程图Fig.6 Proposed MPPT strategy control flow chart

对图6 所示的控制流程图中几个关键模块进行分析如下：

（1）判断风速情况。为避免传统扰动观察法扰动过程中因风速变化带来误判断导致跟踪失败的问题[14]，本文提出的改进型扰动观察法每次扰动系数k 的前提为当前风速情况稳定。这样虽然导致跟踪速度变慢，但由于训练模式只执行一次，一旦找到最佳系数，控制方式转为应用模式。因此，训练模式中关注的重点为保证机组正确追踪到最佳点，本文通过对比相邻两次检测到的功率变化ΔPdc占发出功率Pdc的比值来进行判断，即满足

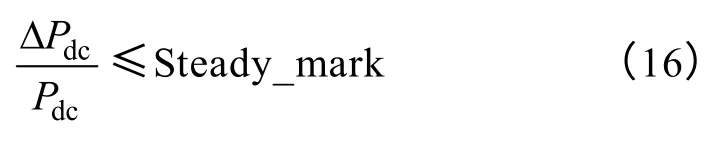
时，认为风速稳定。之后，可改变系数k，进行扰动寻优。

（2）决定Δk 的扰动方向。对系数k 进行扰动时，如Δk＞0，检测到机组的输出功率变化ΔPdc＞0，则继续增大k；反之，则减小k，使Δk＜0。在风速保持不变时，该扰动策略可保证机组追踪到最大功率点。然而，在扰动发生时，风速突变，如风速掉落，Δk＞0 的扰动可能会导致ΔPdc＜0，从而导致扰动策略做出改变k 扰动方向的决策，使得跟踪失败。

为解决此问题，本文对扰动策略进行了改进。由图4a 可知，若关系曲线处于区域1，如位置1，则在k 扰动到最佳系数之前，不管风速增大或减小，均应增加k，以保证k 沿正确方向扰动；而当关系曲线处于区域2 时，则应减小k。因此，为保证扰动更加趋向于沿正确方向进行，改进的扰动策略对历史的扰动方向进行了记录，即设置一个n维的数组sign[n]对前n次扰动方向进行纪录（n=0表示为当前扰动方向，n 取值为偶数以保证扰动方向标志总和为基数），且sign=+1，表示扰动方向为Δk＞0，sign=-1 表示Δk＜0，即

扰动方向的和N 可表示为

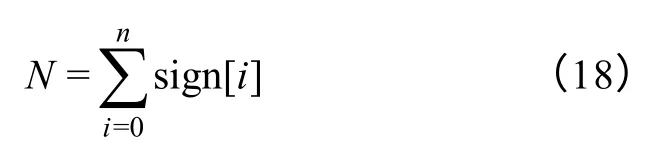
如果N＞0，则说明超过一半的扰动为Δk＞0的扰动，关系曲线k 最有可能处于区域1。因此，不论风速如何变化，下一次将继续保持Δk＞0。当关系曲线k 扰动到区域2 时，随着扰动次数增多，当方向标志超过一半为负时，N＜0，则说明关系曲线k 最有可能已处于区域2，则扰动方向反向为Δk＜0。运用本方法后，可有效避免扰动过程中因风速变化带来的影响。

（3）决定Δk 的扰动幅值。当最佳关系曲线扰动到接近最佳位置时，Δk 开始出现振荡。为消除功率脉动，且使k 更接近，此时应逐渐减小Δk 的扰动幅值。扰动幅值的减小策略采用了类似扰动方向确定的方法，采用一个m 维数组Amp[m]用于记录机组前m次所处的区域。m=0 用于表示k 当前状态，且 Amp[0]=+1，表示 k 当前处于区域 1，Amp[0]=-1，表示k 当前处于区域2。式（19）给出了数学表述

至此，扰动幅值Amplitude 的更新规则为

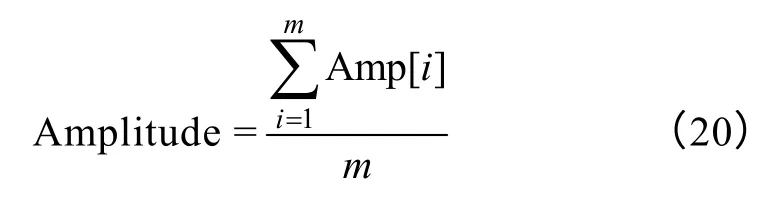
因此，当k 在最佳位置振荡时，即在区域1 与区域2 之间切换时，Amp[m]将随k 所处的区域逐渐更新为+1 及-1。由式（20）决定的扰动幅值将逐渐减小，当小于设定的门限Ath时，可认为k 扰动到最优值。至此，训练模式停止，MPPT 转为采用基于式（11）所示最佳关系曲线的应用模式。

3.3 转速限制的实现

随着风速的增加，机组的转速继续增大。当达到额定转速后，为防止机组因过速而损坏，需对机组的转速进行限制。本文采用对机组直流侧电压进行限制的方法来实现对机组转速的限制。当由式（14）决定的实现机组MPPT 运行的直流侧电压基准超过其额定值VdcN时，对其进行限幅。此后，当风速继续增加时，由于电压基准始终限制为额定值，机组转速也将保持恒定，从而实现了转速的限制。该模态的等效控制原理框图可简化为图7。

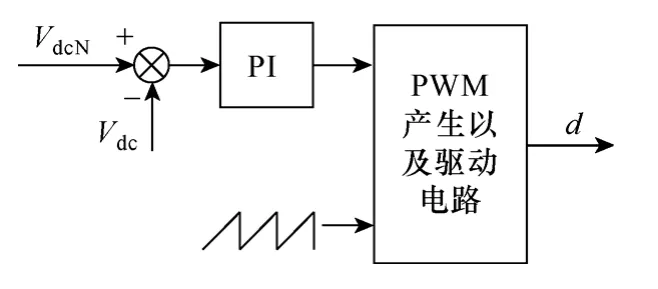
图7 恒转速控制框图Fig.7 Constant speed control block diagram

3.4 功率限制的实现

当风速达到额定风速vN后，机组功率达到额定功率。为防止机组在额定风速以上过功率损坏，需对机组实施恒功率控制。本文所提出的控制策略通过在高风速区增大机组的输出功率，迫使机组进入失速区运行，通过减小机组的风能利用系数实现对机组输出功率的限定。由图2 中所述控制策略可知，在额定风速vN以上，由式（11）决定的直流侧电压基准仍高于额定值，其输出仍被限定为VdcN。但由于机组功率到达了额定值PN，PI1 开始退出饱和，此时直流侧电压的实际参考给定为VdcN减去PI1 的输出值Vcom，电压基准降低。经调节器PI 作用后，机组直流侧电压下降，意味着机组运行转速降低，机组进入失速区运行，达到了限制机组功率的目的。该模态对应的等效控制框图如图8 所示。

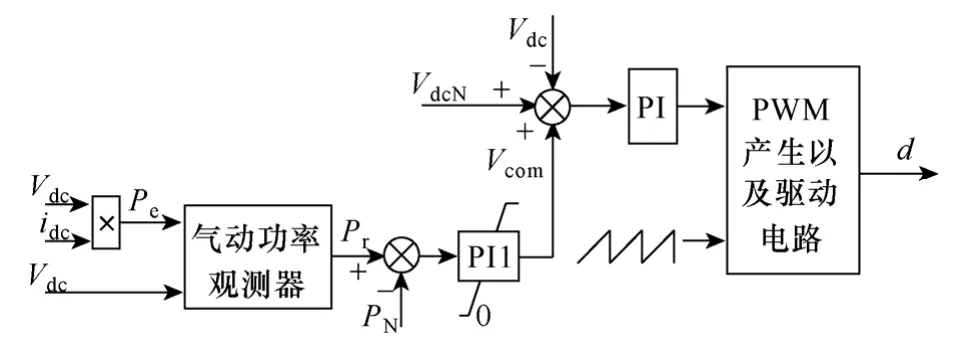
图8 恒功率控制框图Fig.8 Constant power control block diagram

此外，图8 所示的气动功率观测器为基于文献[15]中提出的气动转矩观测器的改进，如图9 所示。图中Trobs、Probs、ωobs、Vdcobs分别为气动转矩、气动功率、机组转速以及直流侧电压的观测值，J为机组的转动惯量。该观测器可较好地观测机组的气动功率，其原理可参考文献[15]分析，此处不赘述。

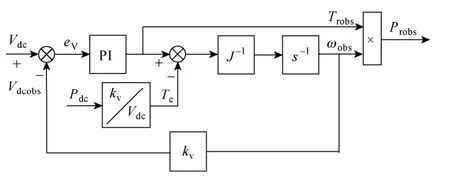
图9 气动功率观测器Fig.9 Aerodynamic dynamic power observer

4 实验验证

为验证本文提出的全风速范围统一功率控制策略的正确性和有效性，将所研究的统一功率控制器分别用于两台具有不同参数的风力发电机组进行控制。两台机组均采用图2 中风力发电系统结构（机组为离网形式），两台机组的参数见表1 和表2，风轮的气动特性曲线分别如图3 和图10 所示。为使实验方便，实验中采用风力机模拟系统来模拟真实风轮的动静态特性，风力机模拟系统不仅方便了在实验室中进行系统实验，而且可方便地模拟不同种类的风况。其工作原理和正确性在前期的研究中已进行了详细分析和验证，这里不再详述，请参见参考文献[16]。实验中所采用的系统控制参数见表3，其中1.2kW 机组输出蓄电池为两节12V/100A·h 的电池串联，端电压24V；10kW 机组输出蓄电池为20节12V/100A·h 的电池串联，端电压240V。此外，为方便监控及记录机组的运行状态（包含系统中关键点数据和相关波形），基于LABView 建立了一套良好的运行状态监控系统，界面如图11 所示。

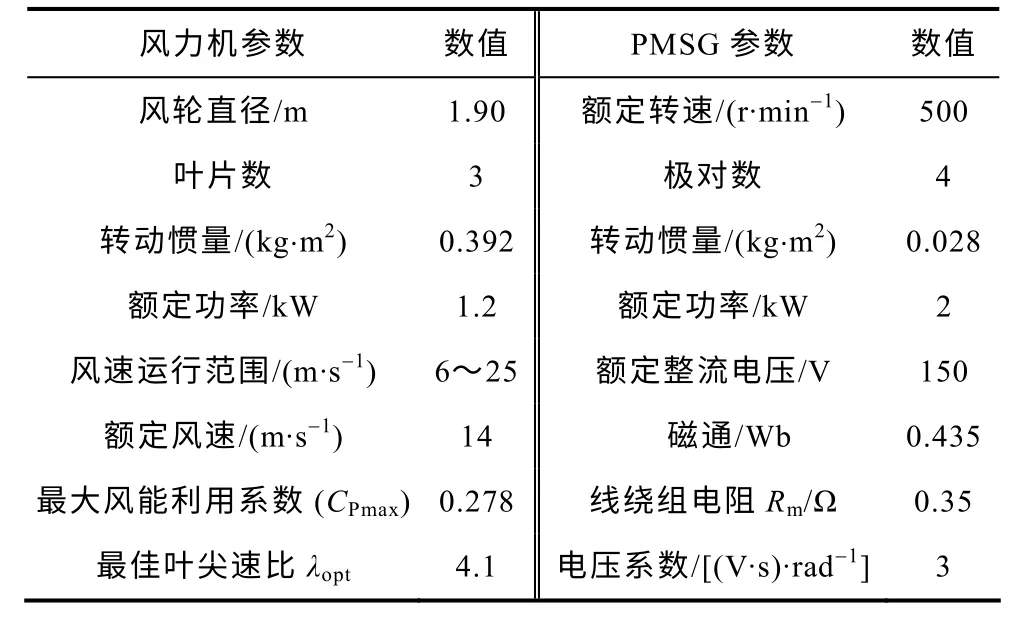
表1 1.2kW 风力发电机组参数Tab.1 Parameters of the 1.2kW WECS

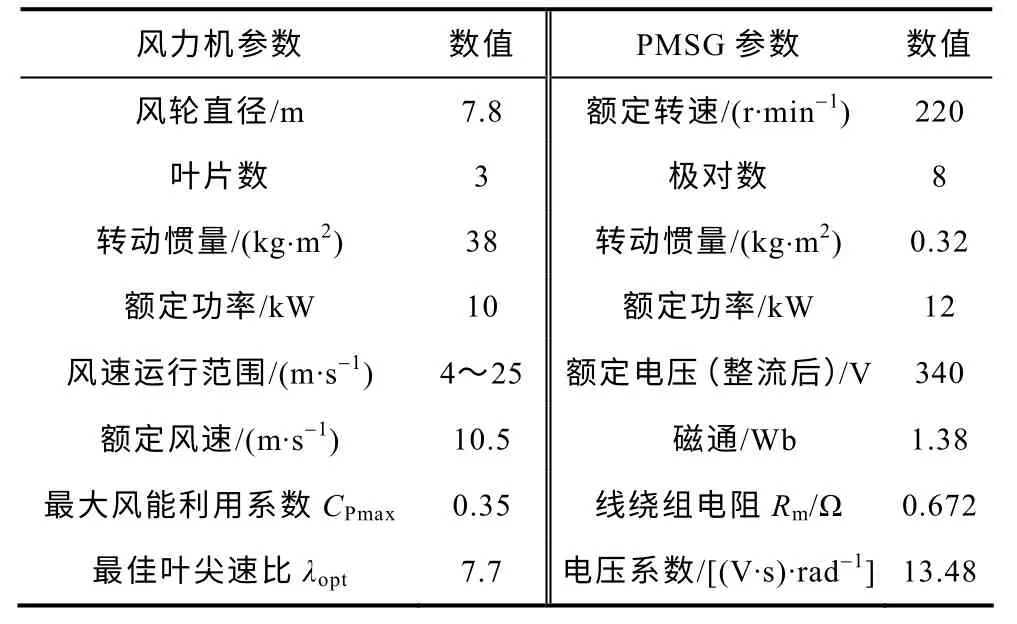
表2 10kW 风力发电机组参数Tab.2 Parameters of the 10kW WECS

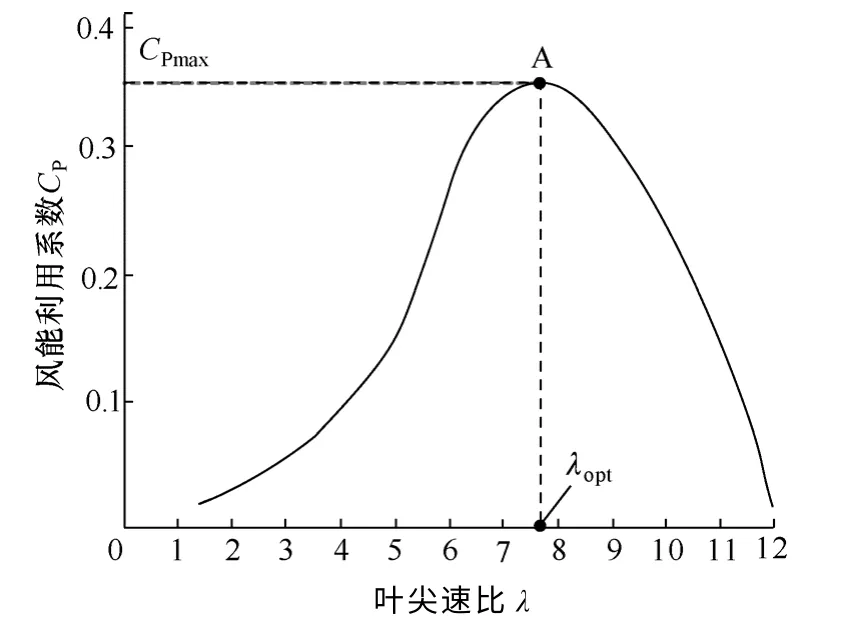
图10 10kW 风力机CP-λ 曲线Fig.10 CP-λ curve of a 10kW wind turbine

表3 实验中采用参数Tab.3 Parameters used in experiments

图11 离网风力发电系统状态监控界面Fig.11 Datum detecting system of the stand-alone WECS

图12、图13 给出了两台机组采用本文提出的统一功率控制策略时在阶跃风速下的实验曲线。从图中可看出，控制系统经过约30s 的训练模式寻优后，k 寻找到最佳关系并保持不变，如图12d、图13d 所示。由图12b、图13b 所示的风能利用系数变化可看出：当风速在额定风速以下变化时，机组首先经过训练模式寻求到CPmax，之后进入应用模式运行以提高机组MPPT 速度，风速在额定风速以下变化时机组始终保持最佳风能利用系数，实现了MPPT 运行。此外，注意到在时间10～15s 区间，风速出现掉落时，本文控制系统仍保持原来的扰动方向不变，直到确定风速确实出现了掉落后才改变扰动方向，从而保证了风速变化时扰动方向的正确性，使机组更快地接近最佳点运行。而随着风速的提高，当直流侧电压达到额定值时（如图12 中90～120s 区段，图13 中50～90s 区段），也即机组转速达到额定转速，控制系统对机组实施恒转速控制，直流侧电压保持额定值恒定不变，如图12c、图13c所示。而当风速超过额定风速后（如图12 中120～150s 区段，图13 中100～150s 区段），为保证机组的安全运行，控制策略通过降低机组的转速（或直流侧电压）迫使机组进入失速区运行，从而减小了机组的风能利用系数，进而减小机组捕获的功率，实现恒功率运行。图12、图13 的实验结果验证了所提出的统一功率控制策略在全风速范围内控制的有效性和通用性。

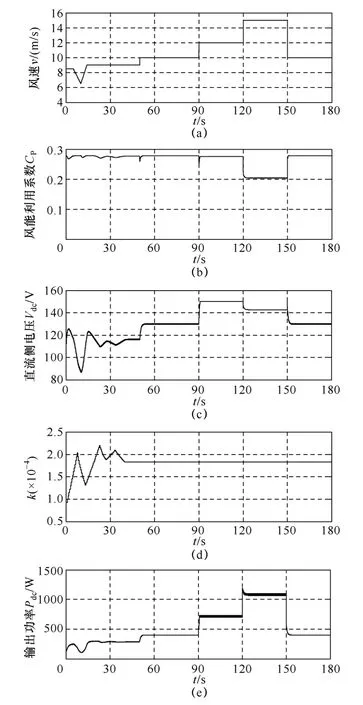
图12 1.2kW 机组实验结果Fig.12 Experimental results performed by 1.2kW turbine under step-changing wind velocity

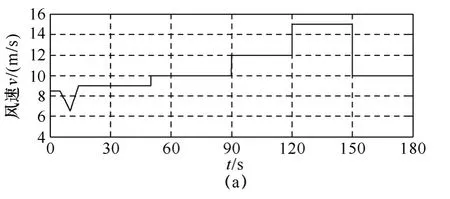
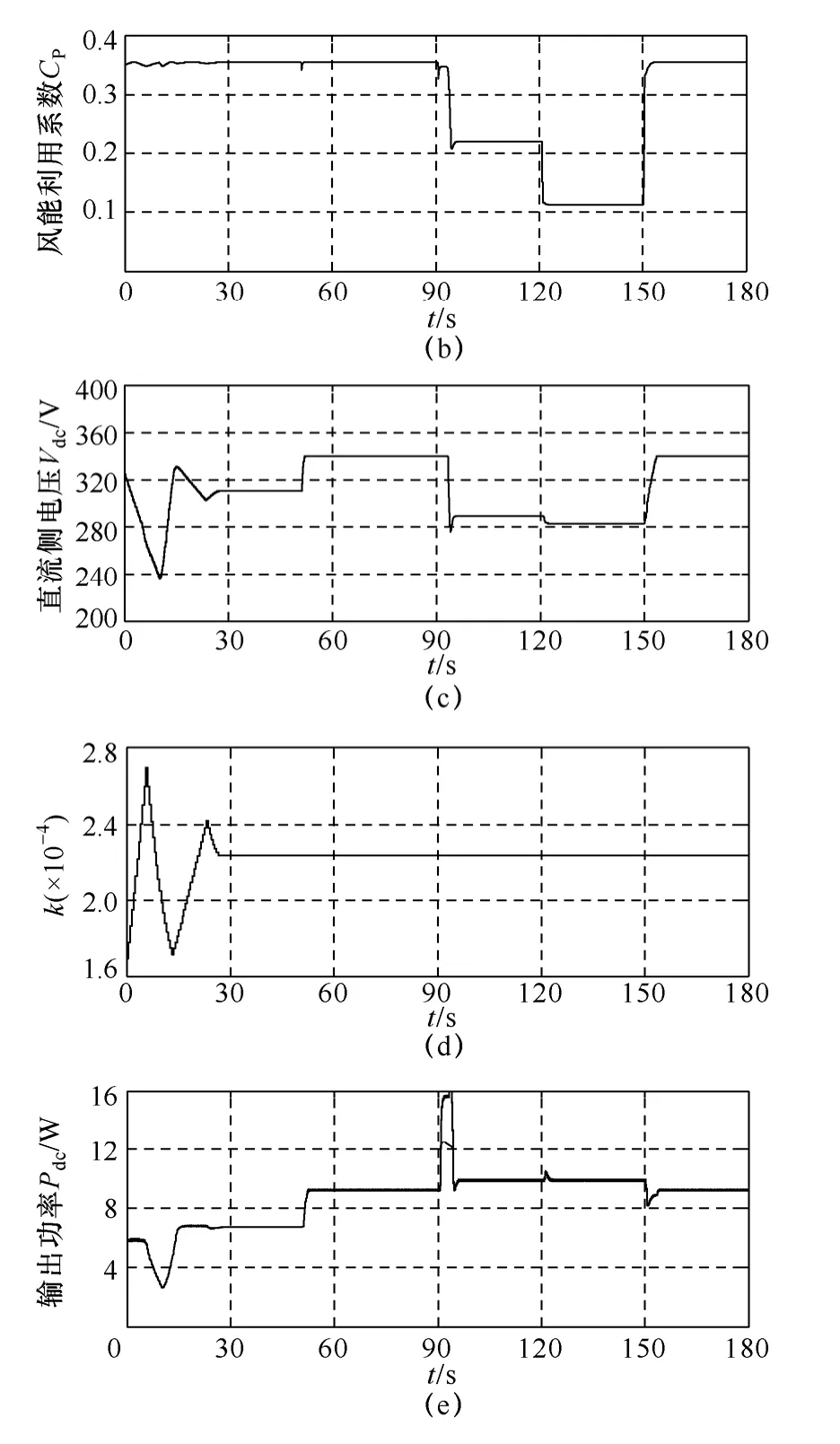
图13 10kW 机组实验结果Fig.13 Experimental results performed by 10kW turbine under step-changing wind velocity

为进一步验证本文控制策略的正确性，对1.2kW 机组在随机风下进行了实验，结果如图 14所示。在0～30s 区间，控制策略运行于训练模式，以寻求最大功率运行点；在30s 时刻，控制策略寻求到机组的最大功率点。此后，控制转换为应用模式运行，当风速小于额定风速时，机组始终保持在最大功率点运行，如30～60s 区间，机组最大风能利用系数始终保持最大值，如图14b 所示。而随着风速增大，机组转速随之增加，当达到额定转速时，控制策略采用恒转速控制，机组转速保持不变，如图14c 中60～70s 区段，机组直流侧电压保持恒定。而当风速超过额定风速后，机组输出功率达到额定值，为防止机组因过功率损坏，本文对机组在额定风速以上实施恒功率控制。如图14 中120～130s区段，该运行区段中风速大于额定风速，控制策略通过降低机组运行的转速（直流侧电压，如图14c所示）使风能利用系数降低（如图14b 所示），从而实现对功率的限制，如图14e 所示。

图14 1.2kW 风力机随机风作用下实验结果Fig.14 Experimental results of the 1.2kW turbine under random wind velocity

5 结论

本文提出一种适用于变速风力发电机组的统一功率控制策略。该控制策略不需要预知风力机的气动特性曲线就可实现机组低风速区的最大功率跟踪控制、高风速区的限转速和限功率控制，具有统一的功率控制性能。此外，控制策略不需检测风速和机组的转速信号，实现了无传感器控制，大大降低了控制的成本。为验证本文提出方法的正确性，将控制策略应用到两台不同的机组进行实验研究，实验结果证明了本文提出方法的正确性和可行性。

[1]尹明,李庚银,张建成,等.直驱式永磁同步风力发电机组建模及其控制策略[J].电网技术,2007,31(15):61-65.Yin Ming,Li Gengyin,Zhang Jiancheng,et al.Modeling and control strategies of directly driven wind turbine with permanent magnet synchronous generator[J].Power System Technology,2007,31(15):61-65.

[2]Geng Hua,Xu Dewei,Wu Bin,et al.Active damping for PMSG-based WECS with DC-link current estimation[J].IEEE Transactions on Industrial Electronics,2011,58(4):1110-1119.

[3]Haniotis A E,Soutis K S,Kladas K G,et al.Grid connected variable speed wind turbine modeling,dynamic performance and control[C].Power Systems Conference and Exposition,New York,2004,2:759-764.

[4]Thiringer T,Linders J.Control by variable rotor speed of a fixed-pitch wind turbine operating in a wide speed range[J].IEEE Transactions on Energy Conversion,1993,8(3):520-526.

[5]Sadre M.Electro-mechanical converters associated to wind turbines and their control[J].Solar Energy,1997,61(2):119-125.

[6]Kazmi M R,Goto H,Guo H,et al.A novel algorithm for fast and efficient speed-sensorless maximum power point tracking in wind energy conversion systems[J].IEEE Transactions on Industrial Electronics,2011,58(1):29-36.

[7]Pucci M,Cirrincione M.Neural MPPT control of wind generators with induction machines without speed sensors[J].IEEE Transactions on Industrial Electronics,2011,58(1):37-47.

[8]赵仁德,王永军,张加胜.直驱式永磁同步风力发电系统最大功率追踪控制[J].中国电机工程学报,2009,29(27):106-111.Zhao Rende,Wang Yongjun,Zhang Jiasheng.Maximum power point tracking control of the wind energy generation system with direct-driven permanent magnet synchronous generators[J].Proceedings of the CSEE,2009,29(27):106-111.

[9]刘其辉,贺益康,赵仁德.变速恒频风力发电系统最大风能追踪控制[J].电力系统及其自动化,2003,27(20):62-67.Liu Qihui,He Yikang,Zhao Rende.The maximal wind-energy tracking control of a variable-speed constant-frequency wind-power generation system[J].Automation of Electric Power Systems,2003,27(20):62-67.

[10]Koutroulis E,Kalaitzakis K.Design of a maximum power tracking system for wind-energy-conversion application[J].IEEE Transactions on Industrial Electronics,2006,53(2):486-494.

[11]Miller A,Muljadi E,Zinger D S.A variable speed wind turbine power control[J].IEEE Transactions on Energy Conversion,1997,12(2):181-187.

[12]Ashraf Ahamed,Li Ran,Jim R.Bumby,New constant electrical power soft-stalling control for small-scale VAWTs[J].IEEE Transactions on Energy Conversion,2010,25(4):1152-1161.

[13]Knight Andrew M,Peters Glenn E.Simple wind energy controller for an expanded operating range[J].IEEE Transactions on Energy Conversion,2005,20(2):459-466.

[14]Haque M E,Kashem M N,Muttaqi M.A novel control strategy for a variable-speed wind turbine with a permanent-magnet synchronous generator[J].IEEE Transaction on Industrial Applications,2010,46(1):331-339.

[15]Hoffmann Rolf.A comparison of control concepts for wind turbines in terms of energy capture[D].Darmstadt:Darmstadt University of Technology,2002.

[16]陈杰,陈家伟,陈冉,等.基于永磁同步电机的风力机动静态特性模拟[J].中国电机工程学报,2011,31(15):40-46.Chen Jie,Chen Jiawei,Chen Ran,et al.Static and dynamic behaviour simulation of wind turbine based on PMSM[J].Proceedings of the CSEE,2011,31(15):40-46.