基于电流闭环和死区补偿的变频驱动调速系统低频振荡抑制

乔鸣忠 夏益辉 朱 鹏 梁京辉 曾海燕

（海军工程大学电气工程学院 武汉 430033）

1 引言

变频器驱动感应电机调速系统在低频（低速）轻载（空载）时经常会出现振荡现象，这种低频振荡引起的过电流轻者使系统跳闸保护，重者烧毁设备。在通用变频调速系统中为了避免低频振荡常采取跳频的方法，即在电机运行过程中避开振荡频率段。近年来，随着电力电子技术的快速发展和各种现代控制方法的提出，交流调速系统在工业领域的应用不断增加，很多场合的变频器工作在低频段，如船用推进变频器工作频率在0～30Hz 之间，传统跳频方法已无法适用。为此，对低频振荡制定相应的抑制策略，已成为当前急需解决的问题。

对于系统低频振荡问题产生的根源，相关的研究文献已很多。文献[1]指出，系统的低频振荡是由滤波元件与电机磁场、转子之间的能量交换引起的，作者建立了变频器驱动感应电机调速系统的小信号模型，并以此为基础，分析了电机参数和滤波器参数对系统稳定性的影响。文献[2]充分考虑了逆变器死区和滤波器的作用，建立了整个系统的小扰动数学模型，指出低频振荡是由电机参数和逆变器参数共同作用的结果。文献[3]对正弦供电感应电机的稳定性进行了研究，对电机的小信号模型采用根轨迹法分析其稳定性，得出感应电机受其参数影响，存在固有不稳定的工作点。文献[4,5]提出一种低频振荡的判断方法，并指出电机参数匹配性和逆变器死区时间是其产生的主要原因。此外，文献[6-11]也对低频振荡产生的原因进行了分析，其结果与前面文献观点基本一致。

尽管低频振荡产生的具体原因不是很明确，但学者们仍提出了几种可以减弱或抑制系统低频振荡的方法。文献[12]提出采用调节定子频率的方法，当电机升速时，将输入频率降低，减少输入功率；而当电机开始降速时，提高输入频率，增加输入功率，使系统的低频振荡得到抑制。其不足之处在于不同电机或同一台电机不同负载，控制环需采用不同的参数。文献[13]采用DPWM 调制策略有效抑制了系统在额定频率一半处出现的不稳定振荡现象，但是应用DPWM 调制策略并不能在整个低频范围内对系统的振荡起到有效的抑制。此外，文献[14,15]采用死区补偿方法减弱了低频振荡的程度，但效果有限。由此可知，提出一种具有应用范围广、性能优异的低频振荡抑制方法显得尤为重要。

本文首先建立了变频驱动调速系统的数学模型，分别对感应电机的小信号模型和逆变器死区对整个系统的影响进行了分析；其次，针对低频振荡现象的特点和逆变器死区时间对系统稳定性的影响，提出了基于电流闭环和死区补偿相结合的低频振荡抑制策略；最后，对基于电流闭环和死区补偿结合的低频振荡抑制策略进行了仿真研究和实验验证，仿真和实验结果表明所提抑制策略是正确可行的。

2 变频驱动调速系统数学模型

2.1 感应电机数学模型

三相感应电机在d-q 旋转坐标系下的数学模型见式（1）、式（2）。

式中rs，rr——定、转子电阻；

Lm，Ls，Lr——励磁电感、定子电感、转子电感；

ωe，ωr——定子旋转角频率和转子旋转角频率。

令式（1）中p=0，可得稳态时电机的状态变量值，即式（2）中下标带“0”的各变量值，求解方程组即可得isd0、isq0、ird0、irq0和Δωr0。

在稳态工作点施加小扰动信号，系统中各变量在稳态点附近会产生一定的增益（这里用Δ表示），忽略Δ2项，整理后可以得到三相感应电机小信号状态方程为

式中，A见下式。

2.2 变频驱动调速系统的小信号模型

死区时间对于变频器的作用，相当于在定子侧串联电阻rdeq，表达式如下[2]：

式中td——死区时间；

fc——开关频率；

Udc——直流侧电压。

由此可知，整个变频驱动调速系统的小信号模型状态方程为

式中，x，B，u均不变，'A见下式。

2.3 变频驱动调速系统稳定性分析

对变频驱动调速系统的小扰动状态方程式（5），采用根轨迹分析方法[1,3]，对实验室的一套变频驱动调速系统进行分析，系统各参数见后文，分别采用仿真分析与解析计算的方法，绘制了系统不稳定区域，如图1 所示，仿真分析所得不稳定区域与解析计算结果基本一致。

由图1 可以看出，系统在恒v/f调速时，低频段系统是不稳定的，说明该系统存在低频振荡现象。

图1 电机空载时系统不稳定区域Fig.1 The unstable area of induction motor fed by inverter without load

3 基于电流闭环和死区补偿相结合的低频振荡抑制策略

3.1 死区补偿方法抑制低频振荡

由文献[2]可知，增大定子电阻会降低系统的稳定性，而死区时间相当于在定子侧串联一个电阻。为此，对逆变器死区时间进行补偿，将有利于系统的稳定。下面针对三种主要的死区补偿方法进行分析。

3.1.1 电流反馈型死区补偿

电流反馈型死区补偿法，通过检测变频器的三相输出电流的极性来确定补偿电压，其表达式如下：

td——死区时间；

fc——开关频率。

usk、分别表示逆变器输出死区补偿前第k相参考电压、死区补偿后第k相参考电压；isk表示第k相检测电流。

该方法由于受死区时间及电流幅值和频率的影响，电流过零点一般存在一定程度的模糊性，因而电流极性的检测精度受到一定的影响。

3.1.2 电压反馈型死区补偿

电压反馈型死区补偿法，是将各相的PWM 输出检测出来，同给定的PWM 波进行比较，得到实际的偏差电压，然后将偏差电压同给定的PWM 波叠加，得到新的给定。其表达式如下：

3.1.3 基于脉冲的死区补偿

由死区形成机理可知[16]，当相电流大于零时，死区时间引起的死区效应使实际脉冲上升沿滞后理想脉冲上升沿td；当相电流小于零时，死区时间引起的死区效应使实际脉冲下降沿滞后理想脉冲下降沿td。

采用基于脉冲的死区补偿方法原则为：当相电流大于零时，在超前理想脉冲上升td时间，加入补偿脉冲至实际脉冲上升沿；当相电流小于零时，在超前理想脉冲下降沿td时间，加入补偿脉冲至实际脉冲下降沿。通过以上方式，使得开关管实际触发脉冲与理想脉冲一致，具体原理如图2 所示。该补偿方法与系统运行频率、载波频率及负载无关，只需检测各相电流的极性，以软件方式实现对死区时间精确的补偿，效果比前两种方式要好。但缺点是，对控制芯片的要求较高，要求在一个PWM 载波周期内进行2 次采样（对脉冲进行不对称采样）。同时，由于采集的电流为当前时刻电流，补偿也存在一定的滞后性（与A-D 采样频率有关）。

图2 基于脉冲的死区补偿方法Fig.2 The dead-time compensated method based on pulse

综上所述，相比于其他两种死区补偿方法，电流反馈型死区补偿方法，具有定子电流易于测量、计算简单、易于实现等优点，但是存在电流过零点难于准确测量的问题。

3.2 基于电流闭环和死区补偿方法相结合的抑制策略

死区补偿方法能有效减弱或抑制受逆变器死区时间主导的调速系统低频振荡，而对于受电机本体参数影响的低频振荡并不是十分有效。由文献[3]可知，即使在正弦供电情况下，感应电机仍有可能存在固有不稳定区域，此时死区补偿是无法采用的。

通过对大量系统低频振荡现象的分析得知，低频振荡的主要特点表现为定子电流和定子线电压的周期性幅值变化。为此，针对低频振荡现象的特点和逆变器死区时间对系统稳定性的影响，提出基于电流闭环和死区补偿相结合的抑制策略。

考虑到逆变器带电机负载，采用SVPWM 方法能更好地通过控制 PWM 电压来跟踪圆形旋转磁场，从而达到更好的控制效果，因此对于逆变器输出电压采用SVPWM 调制策略。

3.2.1 电流闭环和死区补偿相结合的抑制策略

图3 为基于电流闭环和死区补偿相结合的低频振荡抑制原理图。将采集的三相定子电流经过坐标变换至d-q 坐标系中，得到isd、isq分量，这两个分量与相应各轴参考电流的误差，经PI 调节器得到电压，再将这两个分量变换至静止坐标中，计及死区补偿电压，得到参考电压，最后由SVPWM 调制产生参考电压。该方法由于无转子速度闭环，只有简单的两个电流环，其本质上仍是一种开环调速方法，易于实现。

图3 基于电流闭环和死区补偿抑制策略原理图Fig.3 The principle chart of the restrain method based on current close-loop and dead-time compensation

3.2.2 电流闭环控制

在电机工作前已经预知电机未来的工作状态，此时通过电机的稳态数学模型，计算出其稳态时在旋转坐标下的定子电流，将其作为输入电流参考值，定子电流采样值旋转变换后作为反馈，电流误差信号经过PI 控制后输出参考指令电压如式（8），将其变换到两相静止坐标后，得到死区补偿前空间矢量调制的参考电压。

3.2.3 基于电流反馈的死区误差电压补偿

三相自然坐标系下误差电压见式（6），经坐标变换至α-β 静止坐标系下，可以表示为

在两相静止坐标系中，误差电压矢量可以用图4 表示。误差电压取决于电流矢量角，根据α=0、，可将电流矢量平面划分为I～VI 扇区，分别对应isa，isb，isc极性的6 种组合。这6 个扇区，对应逆变器的6 个输出电压误差矢量ΔUs（001～110），这6 个误差电压矢量的方向与6 个非零空间电压矢量的方向完全一致。

图4 电流极性与死区误差电压Fig.4 The current polarity and dead-time error voltage

根据电流矢量所在的扇区，将输出的电压矢量补偿为一个与死区误差电压矢量ΔUs极性相反、大小相等的量，即可抵消死区效应。表给出了三相定子电流isa、isb、isc极性与电压矢量ΔUs和输出误差电压Δusa，Δusb，Δusc之间的关系。

其中，电流矢量扇区判断方式如下：

表 电流矢量与误差电压矢量的关系Tab.The relationship between current vector and error voltage vector

由表可知，为获得补偿电压，必须准确判断三相定子电流的极性。如果用直接检测方法来判断电流极性，在零点附近会有较大误差，容易造成错误补偿。为了避免这一问题，这里采用一种坐标变换和低通滤波相结合的方法，图5 为其原理框图。将检测的三相电流，经过旋转变换至d-q 坐标系中，将得到的isd、isq分量并进行低通滤波后，得到定子电流直流分量isdf、isqf，再将isdf、isqf反变换至自然坐标系下，得到滤波后的各相电流isaf、isbf、iscf，最后，根据滤波后的电流极性来补偿死区时间引起的输出误差电压。

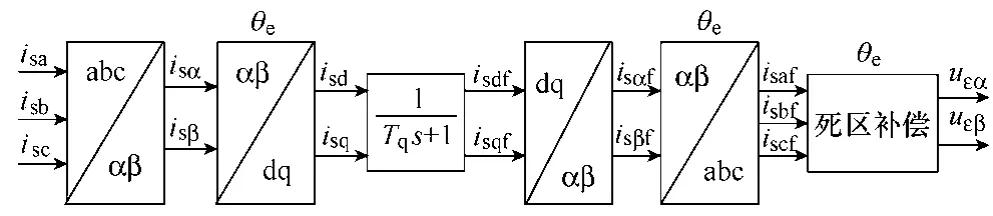
图5 电流极性判别原理框图Fig.5 The principle chart of identifying current direction

将计算得到的死区误差电压补偿量与电流闭环控制在静止坐标系下输出的参考指令电压量相加，得到空间矢量调制最终的参考电压。

4 仿真研究与实验验证

为了验证所提低频振荡抑制策略的正确性，对自行设计的一台130kW 三相感应电机进行了仿真研究和实验验证。电机参数为：额定电压450V，额定频率50Hz，定子电阻0.009Ω，转子电阻0.013 1Ω，定子电感0.034 773H，转子电感0.034 478H，励磁电感0.037 8H，转动惯量15.25kg·m2，极对数2；逆变器参数：直流电容5 000μF，开关频率2kHz，直流侧电压700V，死区时间10μs。

4.1 仿真研究

图6a、6b 为电机空载情况下电机电压、电流和转速波形；图7a、7b 电机带载情况下电机电压、电流和转速波形。

图6 采用所提抑制策略前后电机空载稳态运行结果Fig.6 The static results of induction motor before and after using proposed restrain method without load

图7 采用所提抑制策略前后电机带载稳态运行结果Fig.7 The static results of induction motor before and after using proposed restrain method with load

由图6a、图7a 可以看出，由于定子相电流和定子线电压存在畸变，幅值均发生不规则运动，导致转速波动比较大，系统调速性能差，但带载时系统振荡有所减小，这是由于负载转矩改变了电机的等效参数，通过对其稳态等效电路分析可知，负载的引入相当于减小定子电阻和增大定子漏感，增强了系统的稳定性。图6b、图7b 为采用抑制策略后的电压电流波形，从图中可以看出，定子线电压较好地跟踪了参考线电压；定子相电流波动非常小，基本稳定在期望值附近且接近正弦，转速波动很小，电机平稳运行，低频振荡现象明显得到抑制，整个系统调速性能得到改善，说明采用所提方法抑制低频振荡是切实可行的。

4.2 实验验证

图8 为变频器驱动感应电机调速系统的实验现场，图中电机为自行设计的130kW 三相感应电机，负载为水力测功机。

图8 感应电机实验现场Fig.8 The induction motor experimental location

图9a、9b 为电机空载情况下电机电压、电流和转速波形；图10a、10b 电机带载情况下电机电压、电流和转速波形。由图9a、图10a 中可以看出，系统在定子电流频率fe=10Hz 时发生振荡，定子电流和定子线电压出现周期性波动，测功机界面显示电机转速波动比较大，说明系统发生了低频振荡。由图9b、图10b 中可以看出，采用文中提出的策略后定子电流和定子线电压幅值基本没有变化，水力测功机界面显示电机转速波动比较小，电机运行平稳，所提方法有效地抑制了系统低频振荡，实验结果证明了该方法的正确性。

5 结论

针对感应电机变频调速系统在低频段易出现振荡的问题，本文从系统扰动模型、变频器死区补偿、振荡抑制策略等方面进行了研究，主要结论如下：

图9 采用所提抑制策略前后电机空载稳态运行结果Fig.9 The static results of induction motor before and after using proposed restrain method without load

图10 采用所提抑制策略前后电机带载稳态运行结果Fig.10 The static results of induction motor before and after using proposed restrain method with load

（1）建立了电机及其变频调速系统的小扰动数学模型，采用根轨迹分析方法，绘制了调速系统的不稳定区域，仿真分析所得不稳定区域与理论计算结果基本一致。

（2）分析了多种变频器死区补偿的方法，相比于其他方法，电流反馈型死区补偿方法具有定子电流易于测量，计算简单，易于实现等优点。

（3）提出了基于电流闭环和死区补偿相结合的低频振荡抑制策略。其中电流环用以抑制电机定子电流的波动，使其稳定在期望频率工作点的电流值处；死区补偿用以抵消逆变器死区时间对系统稳定性的影响。仿真与实验结果证明了所提抑制策略是正确可行的。

[1]Lipo T A,Krause P C.Stability analysis of a rectifierinverter induction motor drive[J].IEEE Transactions on Power Apparatus and Systems,1969,86(1):55-66.

[2]郭云珺,王东,刘德志,等.变频驱动感应电机系统稳定性的数学推导与分析[J].电工技术学报,2010,25(9):47-55.Guo Yunjun,Wang Dong,Liu Dezhi,et al.Mathematical deduction and stability analysis of inverter-fed three-phase induction motor drive systems[J].Transactions of China Electrotechnical Society,2010,25(9):47-55.

[3]Nelson R H,Lipo T A,Krause P C.Stability analysis of a symmertrical induction machine[J].IEEE Transactions on Power Application System,1969,86(1):1710-1717.

[4]Koga K,Ueda R,Sonoda T.Stability problem in induction motor drive system[C].IEEE Industry Application Society Annual Conference Record,1988:129-136.

[5]Ueda R,Sonoda T,Koga K,et al.Stability analysis in induction motor driven by V/f controlled generalpurpose inverter[J].IEEE Transactions on Industry Application,1992,28(2):472-481.

[6]Fallside F,Wortley A T.Steady-state oscillation and stabilization of variable-frequency inverter-fed induction motor drives[J].Proceedings of the Institution of Electrical Ehgineeres,1969,116(6):991-999.

[7]Ahmed M M,Sc M,Ph D,et al.Electrical instability in a voltage source inverter-fed induction motor drive at constant speed[J].Proceedings of the Institution of Electrical Ehgineeres,1986,133(4):299-307.

[8]Ueda R,Sonoda T,Koga K.Experimental results and their simplified analysis on instability problem in PWM inverter induction motor drives[J].IEEE Transactions on Industry Application,1989,25(1):86-95.

[9]Lockwood M.Simulation of unstable oscillation in PWM variable-speed drives[J].IEEE Transaction on Industry Application,1988,24(1):137-141.

[10]Colly Roy S,Simlot Anil K,Hallouda Mohab A.Simplified model and corrective measures for induction motor instability caused by PWM inverter blanking time[C].21st Power Electronics Specialists Conference,1990:678-683.

[11]李红梅,李忠杰,刘良成.逆变器供电下异步电动机低频振荡现象的研究[J].电工技术学报,2000,15(3):18-19.Li Hongmei,Li Zhongjie,Liu Liangcheng.Analysis low frequency oscillation of inverter fed asynchronous motor[J].Transactions of China Electrotechnical Society,2000,15(3):18-19.

[12]Mutoh N,Ueda A,Sakai K,et al.Stabilizing control method for suppressing oscillations of induction motors driven by PWM inverters[J].IEEE Transactions on Industrial Electronics,1990,37(1):48-56.

[13]李红梅,孙昌志,李忠杰.采用 DPWM3 调制策略抑制异步电机系统的低频振荡[J].系统仿真学报,2004,16(5):1041-1043.Li Hongmei,Sun Changzhi,Li Zhongjie.Suppression of low frequency oscillation of an induction motor system by DPWM3 modulation strategy[J].Journal of System Simulation,2004,16(5):1041-1043.

[14]Colby R S,Simlot A K,Hallouda M A.Simplified model and corrective measure for induction motor instability caused by PWM inverter blanking time[C].IEEE PESE,1990:678-683.

[15]David Leggate,Kerkman R J.Pulse-based dead-time compensation for PWM voltage inverters[J].IEEE Transactions on Industrial Electronics,1997,44(2):191-197.