电动汽车驱动用内置式永磁同步电机直交轴电感参数计算与实验研究

符 荣 窦满峰

（西北工业大学自动化学院 西安 710072）

1 引言

电动汽车以电能为动力能源，具有零排放、低噪声和节能等优点，目前受到世界各国的青睐。内置式永磁同步电机（IPMSM）以其高效率、高功率密度、高转矩电流比以及更宽的调速区间等优点在电动汽车驱动电机方面获得了广泛的应用[1,2]。

为了获得较高的功率密度，电动汽车驱动用IPMSM 磁路一般设计得比较饱和，使得IPMSM是一个多变量、强耦合、非线性的时变参数系统。而由于IPMSM 转子永磁体的单轴性和凸极效应，使其ABC 轴系下的电机数学模型非常复杂，为了简化电机数学模型，提高电动汽车电驱动控制系统的控制精度，基于d-q 轴系下的直、交轴电感参数Ld、Lq的精确计算显得非常重要[3-6]。

采用有限元法对永磁同步电机参数进行准确计算已被广泛应用[7-10]。文献[11]对电动汽车用双三相永磁同步电机饱和电感特性进行了深入分析，但研究对象是表面式永磁同步电机；文献[12]对考虑交叉饱和影响的永磁同步电机稳态电感参数进行了有限元分析，可文献中负载饱和磁场的有限元分析是针对异步自起动永磁同步电机完成的；文献[13]采用改进的矢量图法对异步自起动永磁同步电机的稳态电感参数进行了有限元计算。由于异步自起动永磁同步电机转子结构上有笼型条，可以直接采用有限元对电机带额定负载起动进行计算，即电机可以从零转速直接自起动进入稳态同步运行状态。

而电动汽车驱动用内置式永磁同步电机转子上无自起动笼型条，有限元带载起动计算困难，本文通过确定带额定负载起动时转子初始位置，实现了30kW 样机有限元带额定负载起动以及负载饱和磁场计算，为样机负载工作点电感参数准确求解提供计算基础。在内置式永磁同步电机电感计算理论的基础上，分别采用忽略交叉饱和影响的有限元法以及冻结磁导率法计算了样机电感参数。并对30kW样机电感参数采用静态交流实验法进行了实验测量。通过对样机实测结果与两种不同有限元计算结果对比表明：忽略交叉饱和影响有限元法可以准确计算样机的静态不饱和电感参数，但负载时样机磁路交叉饱和效应严重，此时采用考虑交叉饱和影响的冻结磁导率法计算样机电感参数更为准确。

2 永磁同步电机电感计算理论

为提高驱动用内置式永磁同步电机有效空间的利用率，电机磁路一般都设计的比较饱和，而内置式永磁同步电机由于转子上永磁体的存在，以及定子绕组磁动势在不同工况下相互作用，引起电机磁路的饱和程度与交叉饱和程度的变化，导致内置式永磁同步电机定转子自感与互感不再是常数[14]。

与电励磁凸极同步电机不同，内置式永磁同步电机的交轴同步电感Lq大于直轴同步电感Ld。根据文献[3]中理想凸极同步电机的A相轴线的气隙磁导表达式，可将内置式永磁同步电机A相轴线的气隙磁导表示为

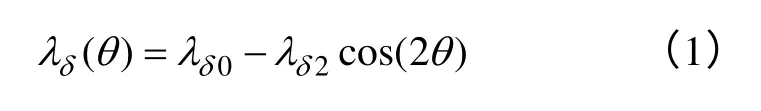
式中0δλ——比磁导的平均值；

λδ2——比磁导的二次谐波幅值；

θ——内置式永磁同步电机转子永磁体 d轴与定子A相轴线间的夹角[3]。

根据文献[3]中理想凸极式同步电机定子绕组电感系数的计算公式，可将内置式永磁同步电机在ABC 坐标系下三相定子绕组自感系数表示为

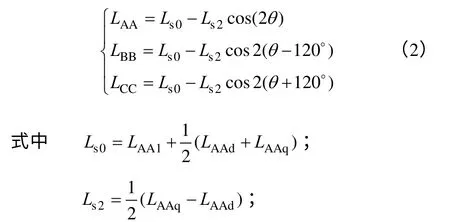
LAA1——永磁同步电机定子A相绕组漏感；

LAAd，LAAq——A相绕组等效直、交轴电感。

同理，根据文献[3]，将内置式永磁同步电机在ABC 坐标系下三相定子绕组间互感系数表示为

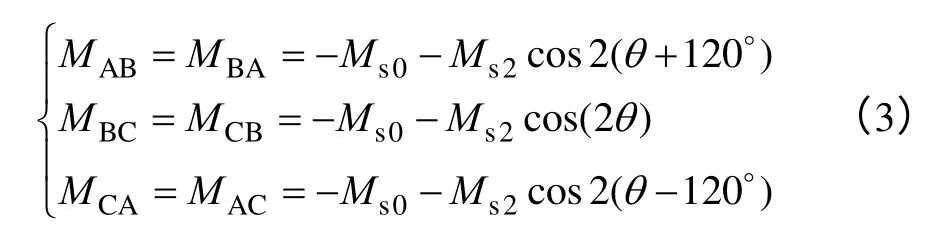
式中 Mσ——两相绕组间的互漏感；

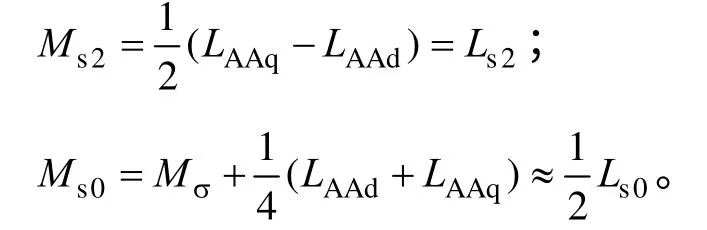
由式（2）与式（3）可知，内置式永磁同步电机定子绕组的自感系数LAA、LBB、LCC，以及定子绕组间的互感系数MAB、MBA、MBC、MCB、MCA、MAC都与转子位置有关，即自感系数与互感系数都是转子位置θ 的函数。

为实现对电动汽车驱动用内置式永磁同步电机的高精度控制，准确计算内置式永磁同步电机直交轴电感参数Ld、Lq非常关键。根据派克变换方程[3]

式中

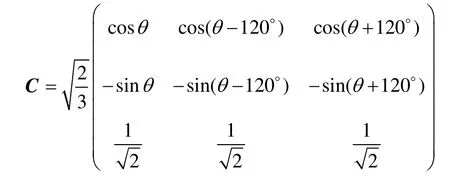
将式（2）、式（3）代入式（4），计算出内置式永磁同步电机在dq 轴系的电感方程为

3 直交轴电感参数的有限元计算方法

有限元数值计算方法不仅考虑了非线性、饱和等因素，而且能够方便地计算出电机内磁场的分布，计算精度高，因此被广泛地应用于永磁同步电机直、交轴电感参数计算中[4-6]。采用3D 有限元计算永磁同步电机直、交轴电感参数时，虽然考虑了电机的端部电感，但在求解3D 有限元模型时，不仅对计算机硬件配置要求高，而且计算量非常大，需要耗费大量时间[12]。因此通常采用2D 有限元模型对电机的直、交轴电感参数进行计算。对2D 有限元模型所忽略的端部电感采用磁路解析法进行计算，以保证永磁同步电机直、交轴电感参数的计算精度[13]。

3.1 忽略交叉饱和影响的直交轴电感有限元计算

根据派克变换方程可知，当永磁同步电机的A相绕组轴线与轴重合时，根据磁链法，电机直轴电枢反应电感Lad可通过式（6）进行计算

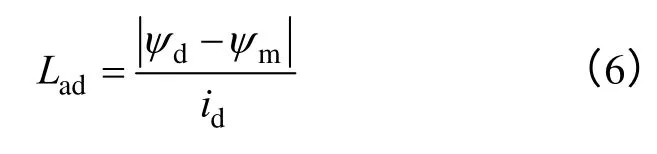
当永磁同步电机的A相绕组轴线与q 重合时，根据磁链法，电机交轴电枢反应电感Laq可通过式（7）进行计算

再利用解析法计算出被忽略的端部电感Lσ1，则内置式永磁同步电机忽略交叉饱和影响的直轴同步电感参数 Ld=Lσ1+Lad，以及交轴同步电感参数Lq=Lσ1+Laq。但上述计算过程是基于静态2D 有限元法对永磁同步电机直、交轴电感参数进行计算，因此，采用该方法计算得到电感参数无法真实反映出在不同负载工况下直、交轴电感参数受交叉饱和的影响所发生的变化。

3.2 冻结磁导率法的直交轴电感有限元计算

冻结磁导率法（FPM）[10]是对电机负载饱和磁场进行有限元计算后，将每个单元的磁导率进行保存，再分别对永磁体单独激励以及定子电流单独激励分别进行线性有限元计算。采用该方法可将不同负载工况下电机的总磁链线性分解为永磁体磁链与定子磁链两部分，从而提高了在不同负载工况下考虑交叉饱和影响的直、交轴电感参数的计算精度[10]。

4 样机计算

4.1 样机参数

本文对所研制的纯电动汽车驱动用30kW 内置式永磁同步电机进行了具体计算，样机截面图如图1 所示，其主要参数见下表。

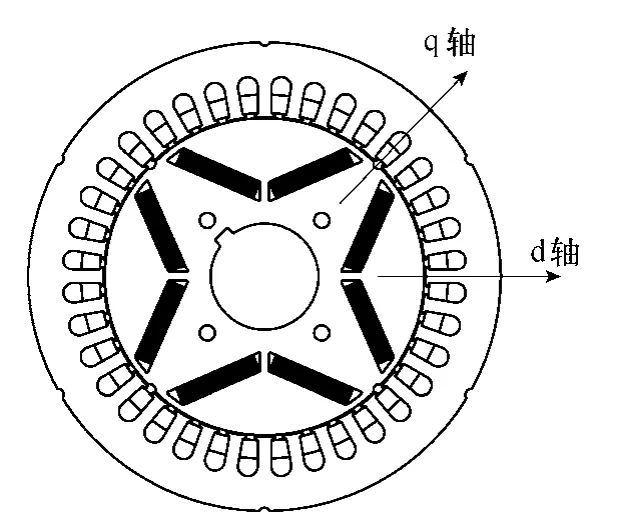
图1 样机截面图Fig.1 Cross section of prototype motor

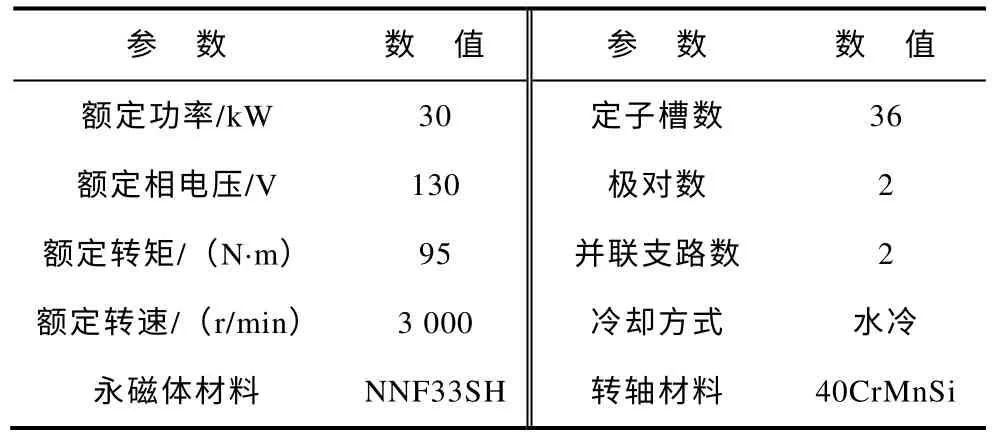
表 样机的主要参数Tab. Main design parameters of prototype motor

4.2 转子初始位置的确定

文献[12,13]所研究的内置式永磁同步电机转子结构上都有笼型条，这种结构永磁同步电机具有异步自起动能力。采用2D 有限元瞬态求解器对异步自起动永磁同步电机负载饱和磁场进行计算时，只要给电机加上对称三相交流电源，再设定负载驱动方式，很容易实现电机带额定负载起动的瞬态有限元计算，即无需外加变频驱动电路，异步自起动永磁同步电机就能够实现从零转速自起动进入稳态同步运行状态。

而本文所研究的电动汽车驱动用30kW 样机转子结构中无自起动笼型条，如图1 所示。导致样机带负载有限元计算比较困难。为了实现对30kW 样机带额定负载起动有限元计算。本文通过确定样机带额定负载时转子初始位置，即对样机模型在不同转子位置的电磁转矩进行参数化求解，确定出样机的矩角特性曲线，进而得到带额定负载时样机对应转子的初始位置为-30°；再设定样机的初始转速为额定转速3 000r/min，加额定负载95N·m，给样机加频率为fN的三相交流电压源，对样机进行了带额定负载起动2D 有限元计算。

通过计算得到30kW 样机带额定负载起动有限元仿真结果，如图2 所示。其中图2a为样机带负载起动时的定子相电流波形。并给出了样机带额定负载稳态运行时样机定子相电压波形与定子相电流波形图，如图2b 所示。

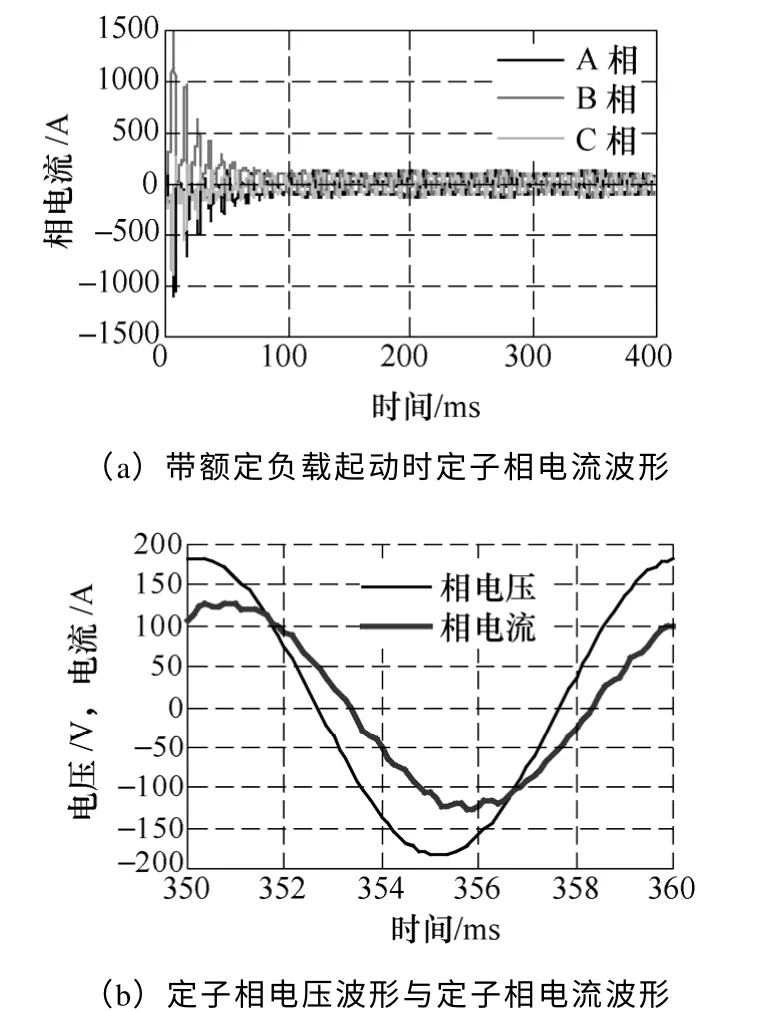
图2 样机带额定负载起动有限元仿真结果Fig.2 Prototype with rated load starting simulation results

4.3 负载饱和磁场计算

通过对30kW 样机额定负载饱和磁场的有限元计算，提取出样机额定负载时气隙磁通密度波形，如图3 所示。在定子电枢磁场与永磁体励磁磁场的共同作用下，样机带额定负载时气隙磁通密度波形明显发生了畸变。

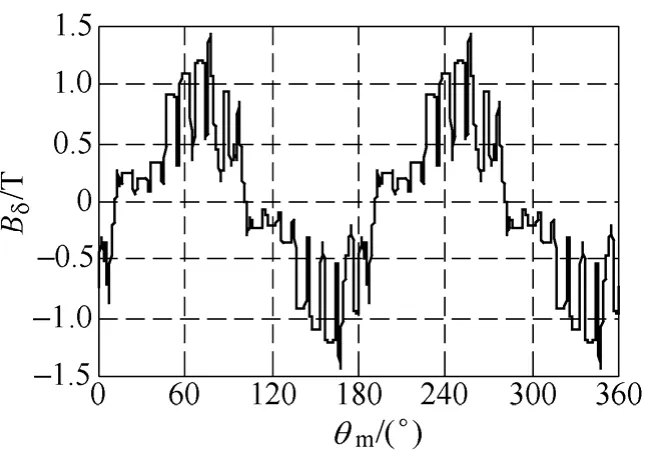
图3 额定负载时样机的气隙磁通密度波形Fig.3 Air-gap flux density of prototype motor at rated-load state

额定负载时样机的磁力线分布图与磁场饱和分布云图，如图4 所示。由于负载电枢反应对永磁体励磁磁场的影响，导致样机额定负载时的磁力线走向不再严格按照d 轴对称，偏向了+q 方向，如图4a 所示。图4b为样机负载磁场饱和分布云图。通过对比图4a 和图4b 发现：在样机磁力线分布密集的区域，磁场饱和程度明显加强，反之，在样机磁力线分布较为稀疏的区域，磁场饱和程度明显减弱。

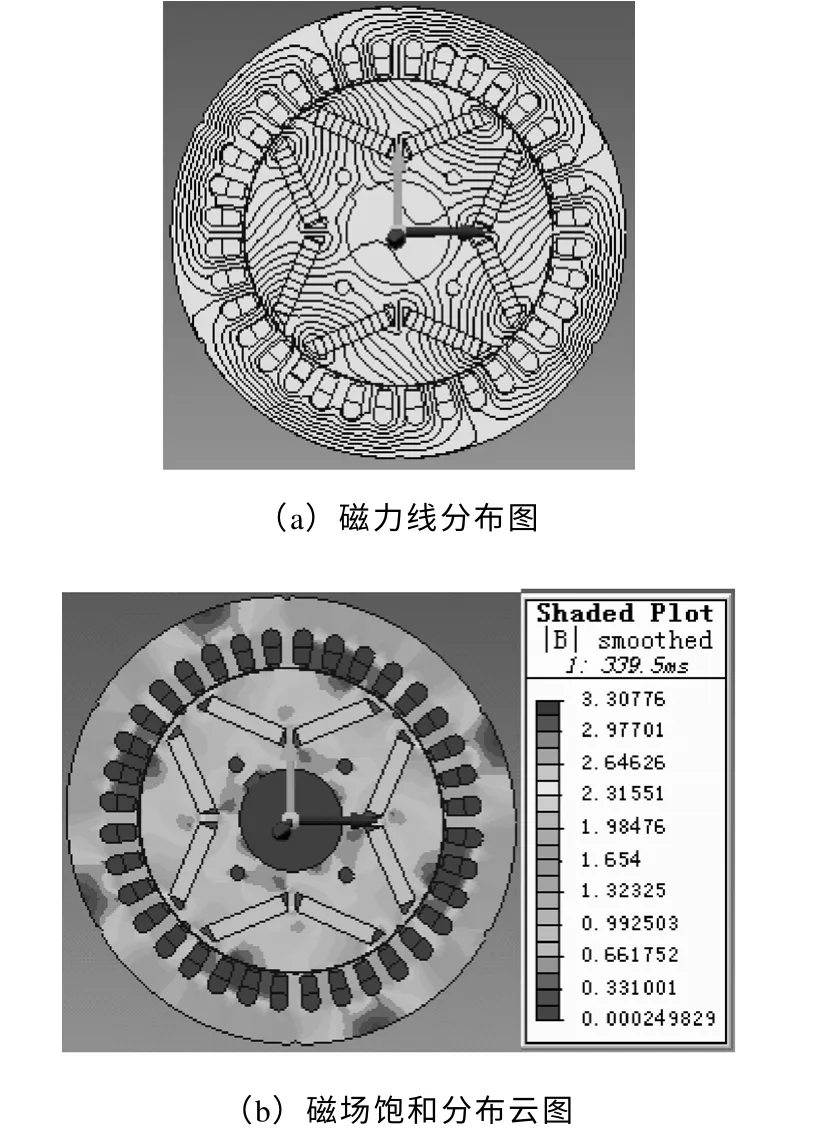
图4 额定负载时的磁力线分布图与磁场饱和分布云图Fig.4 Flux and saturation field contour at rated-load state

4.4 直、交轴电枢反应电感Lad、Laq有限元计算

通过对样机带额定负载稳态运行时负载饱和磁场的计算，结合图2b 所示样机带额定负载稳态运行时的定子相电流波形，计算出样机带额定负载时定子的相电流为80A；再根据样机带额定负载时对应的额定转矩角，分别计算出样机在额定负载点对应的直轴电流Id=-33.8A，交轴电流Iq=72.5A。

为了对30kW 样机直、交轴电感参数从不饱和磁场到负载饱和磁场整个运行区间内的变化情况进行深入研究，结合样机带额定负载时对应的直、交轴电流Id、Iq分别为-33.8A、72.5A，确定出样机的直、交轴电流的变化范围为[-100A,100A]。

本文将分别采用忽略交叉饱和影响的有限元法以及考虑交叉饱和影响的冻结磁导率法，对样机在不同负载工况下的直、交轴电枢反应电感参数Lad、Laq进行计算。

4.4.1 忽略交叉饱和影响的2D 有限元计算结果

根据3.1 节所述忽略交叉饱和影响的有限元计算方法，计算出不同负载工况下忽略交叉饱和影响的样机直、交轴电枢反应电感参数Lad、Laq的变化曲线，如图5 所示。

图5 忽略交叉饱和影响的直、交轴电感有限元计算结果Fig.5 Calculated results of d-and q-axis inductance by FEM ignoring cross-saturation effect

当交轴电流Iq=0，直轴电流Id在[-100A,100A]范围内变化时，计算出样机在不同负载工况下忽略交叉饱和影响的直轴电枢反应电感参数Lad的变化曲线，如图5a 所示。根据样机额定负载点对应的直轴电流Id=-33.8A，由图5a 可以看出，样机在额定负载点对应的直轴电枢反应电感值为0.64mH。样机在额定负载点运行时直轴电流Id为去磁性质，随去磁电流的增大，样机直轴电枢反应电感Lad从Id=-10A 的不饱和磁场对应的0.58mH 增加到Id=-33.8A 的额定负载饱和磁场对应的0.64mH，但由于直轴磁路上永磁体的存在，使得忽略交叉饱和影响的直轴电枢反应电感Lad仅增加了9.3%。

当直轴电流Id=0，交轴电流Iq在[-100A,100A]范围内变化时，计算出样机在不同负载工况下忽略交叉饱和影响的交轴电枢反应电感参数Laq的变化曲线，如图5b 所示。根据样机额定负载点对应的交轴电流Iq=72.5A，由图5b 可看出，样机在额定负载点对应的交轴电枢反应电感值为2.18mH。随着交轴电流Iq的增大，从图5b 可知，样机的交轴电枢反应电感Laq从Iq=10A 的不饱和磁场对应的3.32mH下降到Iq=72.5A 的额定负载饱和磁场对应的2.18mH，交轴电枢反应电感Laq下降了34.3%。说明样机忽略交叉饱和影响的交轴电枢反应电感参数Laq随磁路饱和程度的增加而下降。

4.4.2 冻结磁导率法的2D 有限元计算结果

根据3.2 节所述考虑交叉饱和影响的冻结磁导率法有限元计算方法，计算出不同负载工况下考虑交叉饱和影响的样机直、交轴电枢反应电感参数Lad、Laq的变化曲线，如图6 所示。

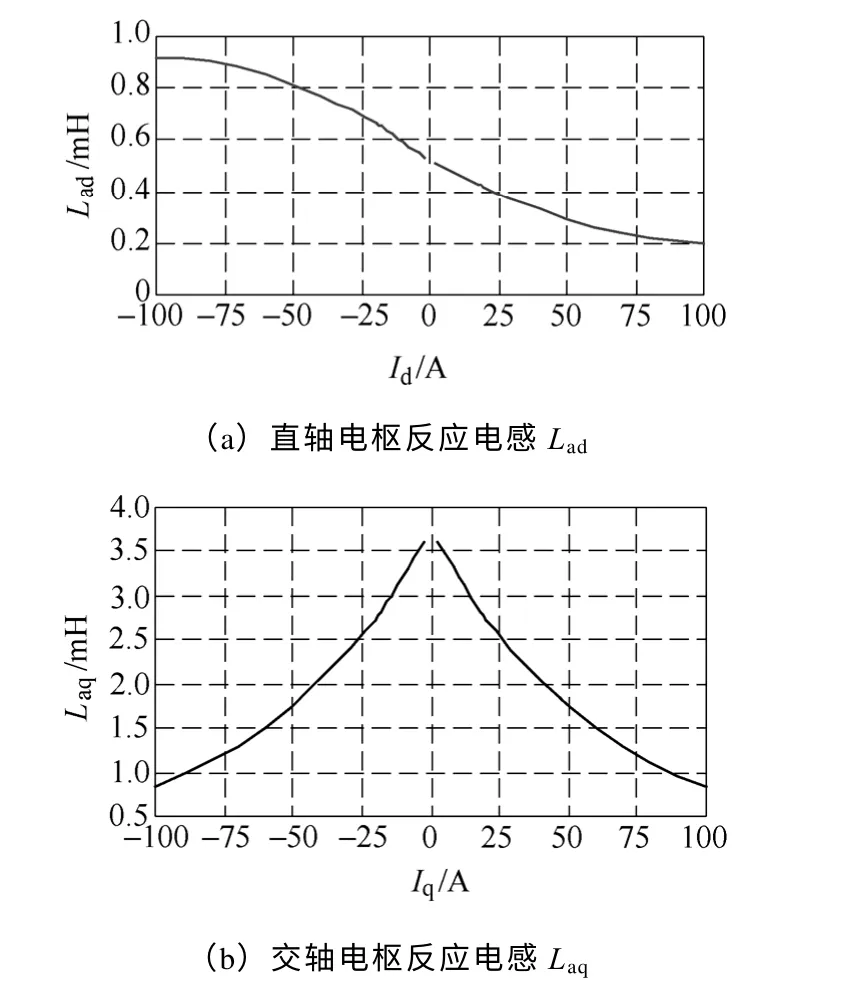
图6 直、交轴电感冻结磁导率法计算结果Fig.6 Calculated results of d-and q-axis inductance by fixed permeability method

根据样机在额定负载点对应的直轴电流 Id=-33.8A，从图6a 可以看出，采用考虑交叉饱和影响的冻结磁导率法计算出样机在额定负载点的直轴电枢反应电感值为0.75mH，与忽略交叉饱和影响的样机在负载额定点的直轴电枢反应电感值0.64mH相比，增大了17%。通过对比图5a 与图6a 可以看出：随着直轴去磁电流Id的增大，受交叉饱和的影响的直轴电枢反应电感参数值Lad比忽略交叉饱和影响的直轴电枢反应电感参数值Lad增加的明显。

根据样机在额定负载点对应的交轴电流 Iq为72.5A，从图6b 可以看出，采用考虑交叉饱和影响的冻结磁导法计算出样机在额定负载点的交轴电枢反应电感值为1.55mH，与忽略交叉饱和影响的样机在负载额定点的交轴电枢反应电感值2.18mH相比，减小了28.89%。通过对比图5b 与图6b 可知，随着交轴电流Iq的增大，样机考虑交叉饱和影响的交轴电枢反应电感Laq比忽略交叉饱和影响的交轴电枢反应电感Laq下降明显，证明了样机交轴电枢反应电感Laq受交叉饱和的影响比较显著。

采用交流电机磁路等效解析法对样机的端部漏感Lσ1进行计算，得到样机端部电感值为0.155mH。再结合以上两种有限元法计算得到的样机在额定负载点的直、交轴电枢反应电感参数Lad、Laq，分别计算出：忽略交叉饱和影响的有限元计算出样机在额定负载点的直轴同步电感Ld=0.795mH、交轴同步电感Lq=2.335mH；考虑交叉饱和影响的冻结磁导率法计算出样机在额定负载点直轴同步电感Ld=0.905mH、交轴同步电感Lq=1.705mH。

对比采用两种有限元方法对样机直、交轴同步电感参数的计算结果发现：负载时样机磁路交叉饱和效应影响严重，使得两种有限元方法计算得到电感参数明显不同；对比图5 与图6 可知：交轴同步电感参数Lq变化的幅度比直轴同步电感参数Ld变化的幅度要明显。

5 实验对比

电动汽车驱动用永磁同步电机电感参数的测试方法主要分为两类：在线辨识法[15]与离线实验室测量法。目前，在线辨识法主要针对表面式永磁同步电机的研究较多，但对内置永磁同步电机电感参数的在线辨识的应用较少。实验室测量法[16]比较常用的有交流静止法、电压积分法、电流衰减法、矢量图法等。针对常用的电感参数实验室测量方法都存在无法在额定负载工况下对电机的电感参数进行精确测试的不足。因此，在样机设计阶段，一般采用静态交流法，加不饱和电流对电机的静态直、交轴电感参数进行实际测试，再与考虑交叉饱和影响的有限元计算结果进行对比分析，最终确定样机在额定负载工况下的直、交轴电感参数。

本文采用静态交流法对30kW 内置式永磁同步样机的电感参数进行实验测量。样机电感实验原理如图7 所示。

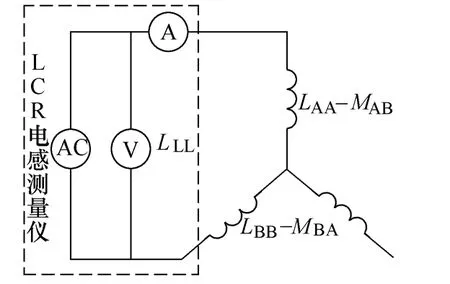
图7 电感实验原理图Fig.7 Inductance experimental schematic diagram

按照图7 对样机定子绕组进行连接，采用LCR电感测量仪对样机的线电感LLL进行测量。为了提高测量精度，采用高精度步进电机来控制样机的转子位置，如图8 所示，测试样机线电感LLL的样机实验平台。

图8 样机实验平台Fig.8 Prototype experiment platform

本文给样机加10A 的不饱和电流对样机线电感参数LLL在不同转子位置下进行了实验测量。根据实测结果给出了样机线电感LLL随转子位置变化曲线图，如图9 所示。

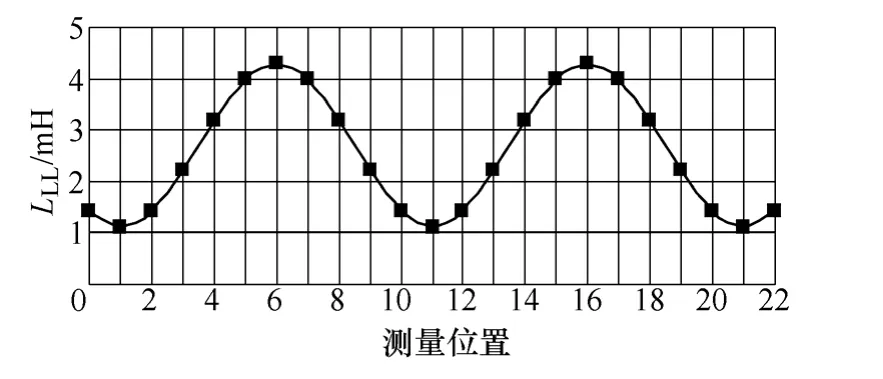
图9 样机线电感LLL测量结果Fig.9 Prototype line inductance LLLmeasurement results

从图9 可以看出，样机线电感LLL随转子位置的变化而变化，而实测得到的样机线电感LLL曲线上对应的最小值 LLLmin=1.12mH、对应的最大值LLLmax=4.29mH。

根据样机的电感实验原理图7 所示，可将样机的线电感LLL表示为

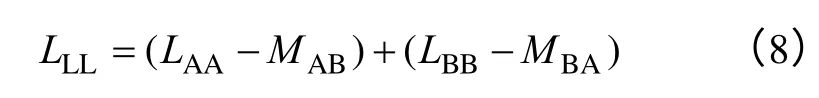
将式（2）、式（3）代入式（8），可得

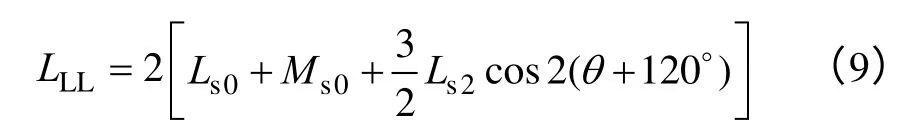
由式（9）得，当θ=-30◦时

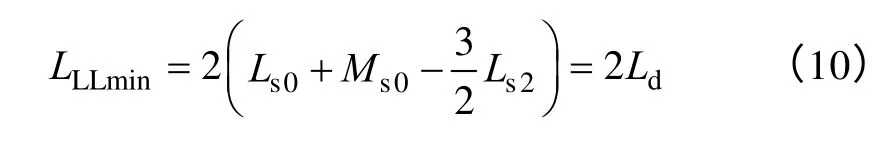
当θ=60◦或θ=-120◦时

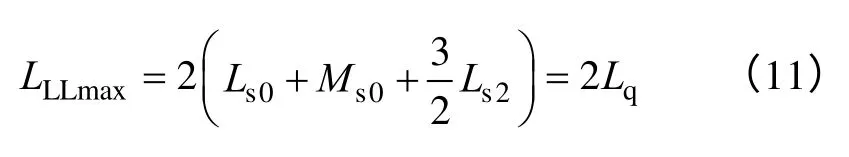
根据式（10）、式（11），以及实测得到的样机线电感对应的最小值 LLLmin为 1.12mH、最大值LLLmax为4.29mH，可计算出样机在10A 不饱和电流作用下的静态直轴同步电感Ld=0.56mH，以及静态交轴同步电感Lq=2.145mH。

对样机静态直、交轴电感参数进行测量时，只给样机加了10A 的不饱和电流值，而对样机直、交轴电感参数采用两种不同有限元法是在[-100,100]A 整个工况下进行计算的。其中，采用忽略交叉饱和影响的有限元法计算出样机在额定负载点直、交轴同步电感值分别为0.795mH、2.335mH；采用考虑交叉饱和影响的冻结磁导率法计算出样机在额定负载点直、交轴同步电感值分别为 0.905mH、1.705mH。

将样机静态不饱和电感参数实测值与两种不同有限元法的额定负载点计算结果进行比较发现：忽略交叉饱和影响的电感参数计算值与静态实测电感值相吻合，采用冻结磁导率法计算的额定负载点q轴电感值比静态实测q 轴电感值减小了20.5%，冻结磁导率法计算的额定负载点d 轴电感值比静态实测d 轴电感值增大了38.1%。说明采用忽略交叉饱和影响有限元法可以准确计算样机的静态不饱和电感参数，但负载时样机磁路交叉饱和效应严重，此时采用考虑交叉饱和影响的冻结磁导率法计算样机电感参数更为准确。

6 结论

（1）本文通过确定转子上无自起动笼型导条的电动汽车驱动用30kW 内置式永磁同步电机带额定负载起动时转子初始位置，实现了30kW 样机有限元带额定负载起动以及负载饱和磁场计算。为样机在不同负载工况下直、交轴同步电感参数的精确求解提供了计算基础。

（2）本文分别采用忽略交叉饱和影响的有限元法以及考虑交叉饱和影响的冻结磁导率法对30kW样机的交、直轴电感参数进行计算；并对样机采用静态交流实验法进行了实验测量。通过样机的两种有限元法电感参数计算结果与样机静态不饱和电感参数实测值对比分析表明：采用忽略交叉饱和影响的有限元法可以准确计算出样机静态不饱和电感参数值，但负载时样机磁路交叉饱和效应严重，此时采用考虑交叉饱和影响的冻结磁导率法计算样机电感参数更为准确。

[1]Zhu Z Q,Howe D.Electrical machines and drives for electric,hybrid,and fuel cell vehicles[J].IEEE Proceedings,2007,95(4):746-765.

[2]Chau K T,Chan C C,Liu Chunhua.Overview of permanent magnet brushless drives for electric and hybrid electric vehicles[J].IEEE Transactions on Industrial Electronics,2006,55(6):2246-2257.

[3]汤蕴璆,张奕黄,范瑜.交流电机动态分析[M].北京:机械工业出版社,2005.

[4]Zhou Ping,Lin Dingsheng,Georg W.Determination of d-q axis parameters of interior permanent magnet machine[J].IEEE Transactions on Magnetics,2010,46(8):3125-3128.

[5]Nee Hans Peter,Lefevre L.Determination of d and q reactance of permanent-magnet synchronous motors without measurements of the rotor position[J].IEEE Transactions on Industry Applications,2000,36(5):1330-1335.

[6]Yamamoto Shu,Kano Takashi,Yamaguchi Yoshihiro,et al.A method to determine direct-and quadratureaxis inductances of permanent magnet synchronous motors[J].Electrical Engineering in Japan,2010,171(3):41-50.

[7]白玉成,唐小琦,吴功平.内置式永磁同步电机弱磁调速控制[J].电工技术学报,2011,26(9):54-59.Bai Yucheng,Tang Xiaoqi,Wu Gongping.Speed control of flux weakening on interior permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2011,26(9):54-59.

[8]程树康,李春艳,寇宝泉.具有变磁阻励磁回路的永磁同步电动机电感参数[J].电工技术学报,2008,23(2):6-10.Cheng Shukang,Li Chunyan,Kou Baoquan.Research on inductance of PMSM with variable magnetic reluctance in exciting circuit[J].Transactions of China Electrotechnical Society,2008,23(2):6-10.

[9]汤蕴璆,梁艳萍.电机电磁场的分析与计算[M].北京:机械工业出版社,2010.

[10]Kwak Sang Yeop,Kim Jae Kwang.Characteristic analysis of multilayer-buried magnet synchronous motor using fixed permeability method[J].IEEE Transactions on Energy Conversion,2005,20(3):549-555.

[11]郑萍,王勃,吴帆.电动汽车用双三相永磁同步电机饱和电感特性分析及计算方法[J].电工技术学报,2013,28(7):19-25.Zheng Ping,Wang Bo,Wu Fan.Analysis and calculation method of saturated inductance of a dual-three phase permanent-magnet synchronous machine for electric vehicles[J].Transactions of China Electrotechnical Society,2013,28(7):19-25.

[12]李和明,张健,罗应立.考虑交叉饱和影响的永磁同步电机稳态参数有限元分析[J].中国电机工程学报,2012,32(12):104-110.Li Heming,Zhang Jian,Luo Yingli.Finite element analysis of PMSM steady state parameters considering cross-saturation effect[J].Proceedings of the CSEE,2012,29(18):104-110.

[13]李和明,张健,刘明基.基于时步有限元的永磁同步电机稳态参数改进计算方法[J].电工技术学报,2012,27(4):35-41.Li Heming Zhang Jian,Liu Mingji.An improved calculation method for steady-state parameters of PMSM with T-S FEM[J].Transactions of China Electrotechnical Society,2012,27(4):35-41.

[14]任雷,崔芮华,王宗培,等.永磁同步电机绕组电感的饱和效应[J].电工技术学报,2000,15(1):21-25.Ren Lei,Cui Ruihua,Wang Zongpei,et al.Saturation effect of PMSM windings inductance[J].Transactions of China Electrotechnical Society,2000,15(1):21-25.

[15]石晶合.永磁同步电机非线性及谐波参数的闭环辨识系统研究[D].哈尔滨:哈尔滨工业大学,2010.

[16]宫海龙,柴凤,程树康.高转矩永磁轮毂电机电感参数研究[J].中国电机工程学报,2010,30(21):61-66.Gong Hailong,Chai Feng,Cheng Shukang.Research on inductance parameters of high torque permanent magnet in-wheel motor[J].Proceedings of the CSEE,2010,30(21):61-66.