基于反推控制的永磁同步电动机速度的模糊控制

刘栋良 崔言飞 赵晓丹 陈镁斌

（1.杭州电子科技大学自动化学院 杭州 310018 2.卧龙电气集团有限公司 上虞 312300）

1 引言

永磁同步电机具有结构简单、运行可靠、体积小、效率高、容易维护等优点，在伺服系统中得到了广泛地应用。但是由于永磁同步电动机中转速和电流的非线性耦合，使用一般线性控制方法难于达到控制性能的要求。为了实现对其有效控制，当前主要采用非线性控制方法有变结构控制[1,2]、微分几何[3]和无源控制[4]等。但这些非线性控制的设计方法比较复杂，不易实现。

反推控制理论的提出在电机控制领域得到了广泛的关注，并被应用于永磁同步电机伺服控制系统中[5]。反推控制是一种有效的非线性控制设计方法，它不但能够实现永磁同步电动机系统的完全解耦，而且设计过程简单。近年来，反推控制在永磁同步电动机系统中的应用取得了一些成果[6-8]。文献[9]把反推控制策略应用于永磁同步电动机速度的跟踪系统中，简化了一般系统设计过程，减少了系统控制中的调节参数数目，保证了系统具有全局稳定性，并实现了良好的速度跟踪，但它没有考虑系统中参数的变化对系统性能带来的影响。文献[10]采用自适应控制与状态反馈精确线性化控制相结合，所给出的控制器设计是建立在电机角速度与电流乘积项基础上，使控制器的设计难度大大增加。文献[11]提出了自适应控制与反推控制相结合应用于具有不确定参数的永磁同步电机速度跟踪系统中，该方法针对控制系统中电阻和负载的实时估计，在一定程度上实现了对扰动的抑制，但它没有考虑系统的速度和电流反推调节器中反推参数对系统性能的影响。由于系统设计中参数的选取对系统稳定性和动态性能有很大影响，因此永磁同步电动机调速系统中，反推调节器中速度和电流的反推参数的选取十分重要。

针对上述问题，本文提出了把模糊反推控制应用于永磁同步电动机的速度控制系统中，通过模糊原理设计出模糊控制器，根据设定的模糊规则对反推参数进行实时调节，优化参数。采用模糊反推控制不但实现了永磁同步电动机系统的完全解耦，而且能够增强系统抗干扰性，实现快速的速度跟踪。Matlab 仿真和实验结果表明，通过模糊控制器对反推控制参数的在线修正，大大提高了系统的静态和动态性能，保证了系统的全局的稳定性，并使系统具有较强的鲁棒性。

2 永磁同步电机数学模型

基于同步旋转转子dq 坐标下的表面式的永磁同步电动机的定子电压[12]如下：（其交直轴电感近似相等，即Ld=Lq=L）

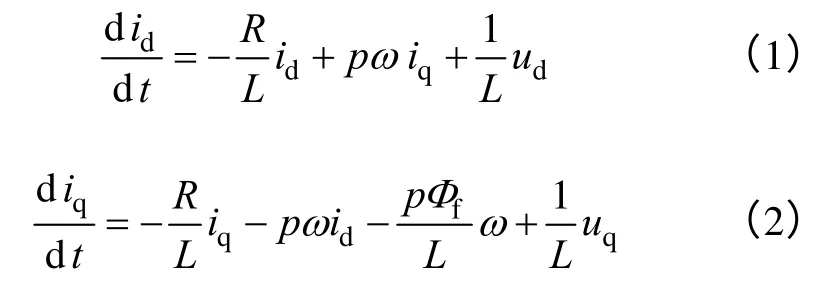
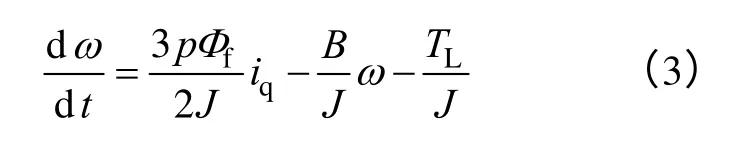
式中 ud，uq——d、q 轴定子电压；

id，iq——d、q 轴定子电流；

R——定子电阻；

Φf——永磁磁通；

L——定子电感；

p——极对数；

J——转动惯量；

B——粘滞摩擦系数；

TL——负载转矩；

ω——转子机械角速度。

3 系统控制的设计

3.1 反推控制设计

反推设计过程是逐步递推的设计过程。该过程中引进了虚拟状态和虚拟控制函数，前面的子系统必须通过后面子系统的虚拟控制才能达到目的。它是通过从原系统方程中选取状态构造新的子系统，并构造Lyapunov 函数，设计虚拟控制函数，使子系统稳定，然后逐步设计，直到得到系统实际控制，保证整个系统稳定[13]。

在永磁同步电动机控制系统中，为了实现电机实际转速跟踪期望的参考转速，需要利用反推控制理论，设计反推控制器。反推控制器的设计过程参考文献[9]。

在设计过程中，首先，选择速度的跟踪误差e为系统的状态变量，为了实现速度的全局渐进跟踪，构造Lyapunov 函数，并根Lyapunov 据稳定判据，引入了虚拟电流控制函数为

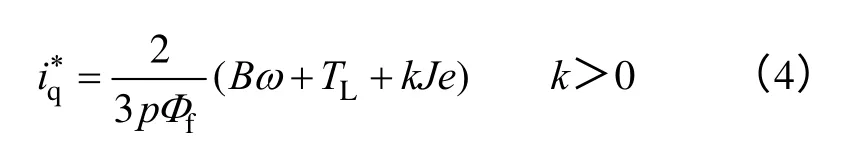
然后，为了实现对虚拟参考电流的跟踪，选择电流跟踪误差ed、eq为虚拟误差变量

由e、ed、eq构成新的子系统，为了实现电流对参考电流的跟踪，构造新的子系统的Lyapunov 函数，并由稳定判据，得到系统实际控制量uq和ud为

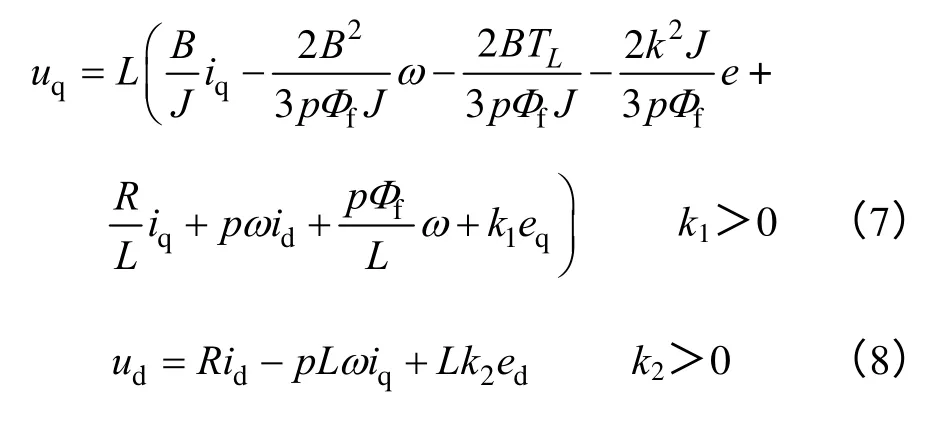
通过式（7）和式（8）便得到了系统的实际控制量。

由式（4）设计的速度环的反推控制器，式（7）和式（8）设计的电流环的反推控制器，不但能够使得永磁同步电动机系统达到速度的渐近跟踪，同时电流的稳定跟踪能够使得系统具有快速的响应速度。

3.2 模糊控制器的设计

根据反推控制器的设计，可知永磁同步电动机系统的反推控制调节参数有三个，即速度ω 调节参数k，转矩电流iq的调节参数k1和磁通电流id调节参数k2。为了使系统达到快速的速度跟踪和较强的鲁棒性，不但要求反推控制参数k＞0，k1＞0，k2＞0，还需要根据系统不同运行状态调节k，k1，k2数值。通过大量仿真证明k2的取值变化对系统运行状态影响极小，其变化可以不考虑，因此只需要保证满足系统稳定条件，即k2＞0。所以本控制系统只需要调节的参数只有k 和k1。本文通过模糊控制器的设计[14-16]，对反推控制参数进行优化处理，使系统实现较强的伺服性能。

系统设计的模糊控制器是以速度偏差e 和偏差变化率ec为输入量，反推参数修正值Δk、Δk1为输出量。先找出参数k、k1与e 和ec之间的模糊关系，在运行中不断检测e 和ec，再根据模糊控制原理对参数k、k1进行在线修改，以满足在不同e 和ec时对参数k 和k1的不同要求。

通过大量测试，得出在不同e 和ec下被控过程对参数k、k1的整定要求，总结以下规律：

（1）当|e|较大时，为了使系统有较好的可快速跟踪性能，应取较大k 和较小的k1。

（2）当|e|中等时，为了减小系统超调，应取较小k 和较大的k1。

（3）当|e|较小时，为了使系统有较好的稳态性能和抗干扰能力，应取较大的k 和适当的k1。

设计模糊控制器时，首先需要确定输入与输出变量的模糊子集合的论域和隶属函数。由于模糊控制器的输入、输出变量都是精确量，而模糊推理是针对模糊量进行的，所以需要先对输入变量进行模糊化。定义输入变量e、ec和输出变量Δk、Δk1的模糊集论域均为[-4 4]，输入、输出变量模糊子集均为{NB NS ZO PS PB}，且其隶属函数采用三角形函数，如图1 所示，由此可得到模糊子集的隶属度。

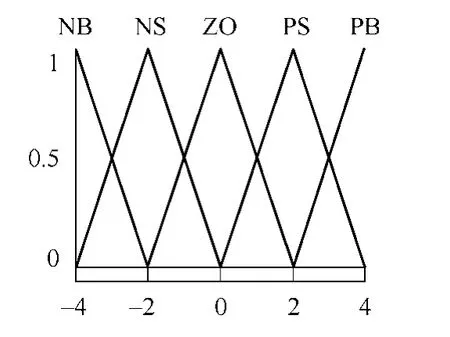
图1 输入和输出隶属函数图Fig.1 Input and output membership functions diagram

模糊控制器根据被控对象的状态自动调整输出变量Δk、Δk1的值，并对反推参数进行在线校正，计算公式为

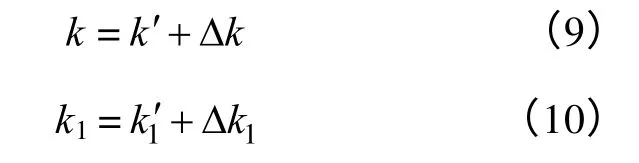
根据应用经验和前面总结规律，确定两个输出量与输入量的模糊控制规则分别见表1 和表2。模糊推理采用Mandani 型模糊推理算法。

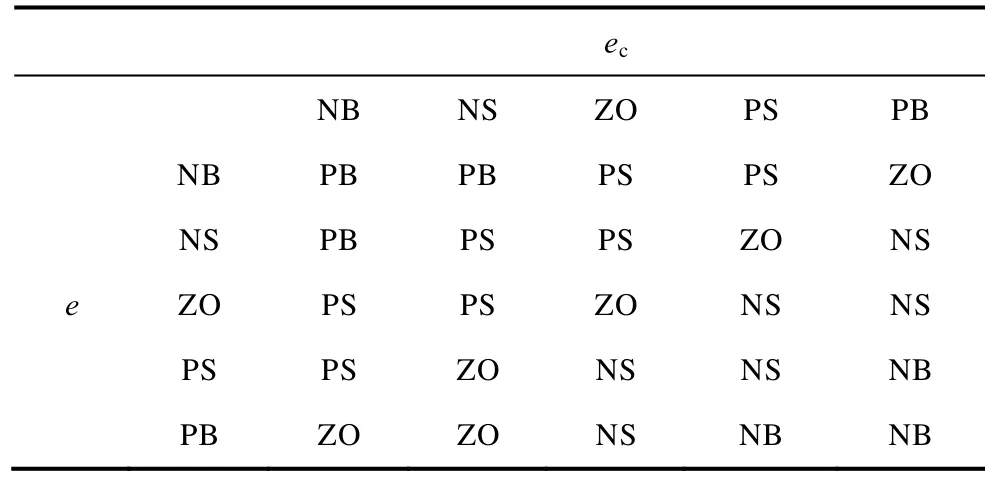
表1 Δk 的模糊规则表Tab.1 Fuzzy rule table of Δk

表2 Δk1的模糊规则表Tab.2 Fuzzy rule table of Δk1

根据Mandani 模糊推理方法，模糊控制的输出曲面如图2 和图3 所示。

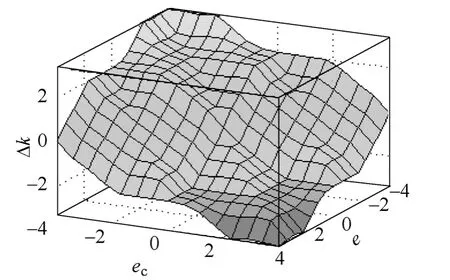
图2 Δk 的模糊推理输出曲面Fig.2 Fuzzy reasoning output surface of Δk

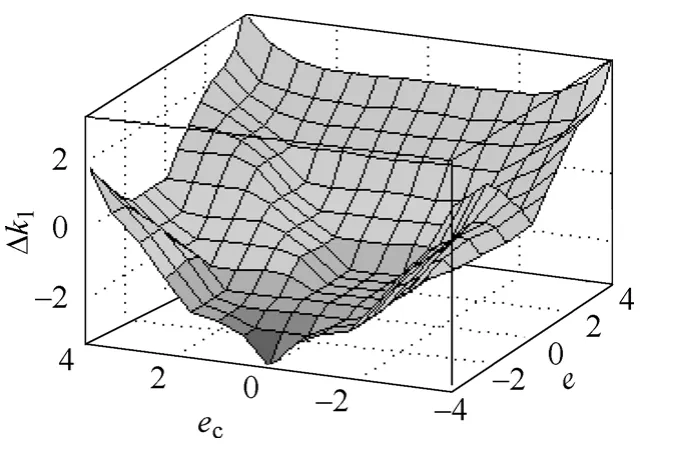
图3 Δk1的模糊推理输出曲面Fig.3 Fuzzy reasoning output surface of Δk1

经模糊推理后，模糊控制输出为模糊量，不能直接用于控制对象，还需对模糊量要进行去模糊化，并将其转换到控制对象所能接受的基本论域中去，去模糊化处理采用重心法。

4 系统仿真与实验结果

4.1 仿真实验

图4 所示为永磁同步电动机系统的模糊反推控制结构框图。用于仿真的1kW 的永磁同步电动机参数为：极对数p=4，转动惯量J=0.001kg·m2，永磁磁通Φf=0.8Wb，粘滞摩擦系数B=0.000 1，定子电感L=0.006H，定子电阻R=2Ω。

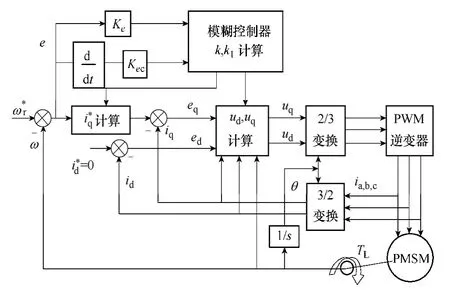
图4 PMSM 的模糊反推控制系统框图Fig.4 Fuzzy backstepping control diagram of PMSM

设定电动机的初始跟踪速度为300r/min，初始负载为零，在0.4s 时突加负载5N·m，在0.7s 时负载降为0N·m。仿真中反推参数初始值取为：

当电动机给定参数发生变化时，在没有模糊控制环节的情况下，反推控制系统仿真结果如图5所示，图5a为转速变化波形，图5b为转矩变化波形，图5c为三相定子电流变化波形。模糊反推控制系统仿真结果如图6 所示，图6a为转速变化波形，图6b为转矩变化波形，图6c为三相定子电流变化波形。

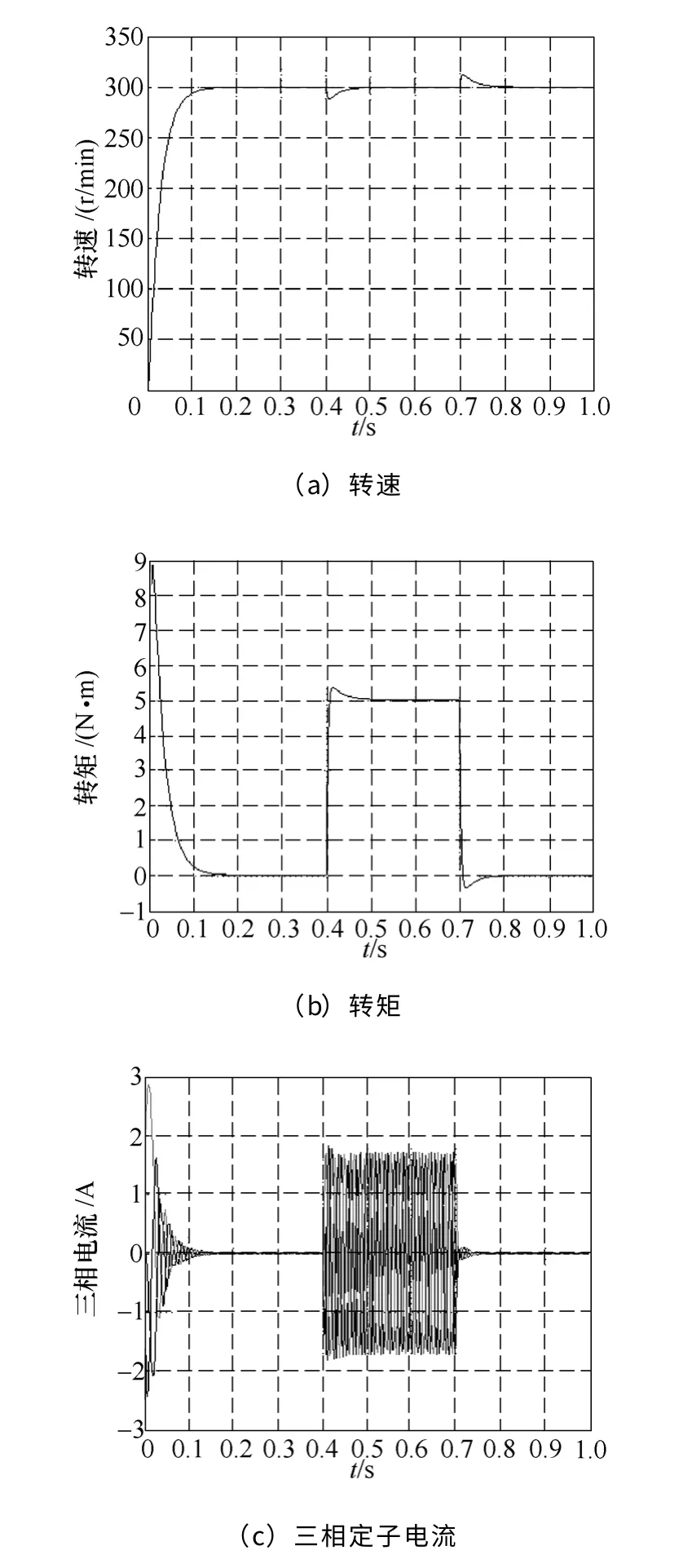
图5 反推控制的仿真结果Fig.5 Transient responses with backstepping control by simulation

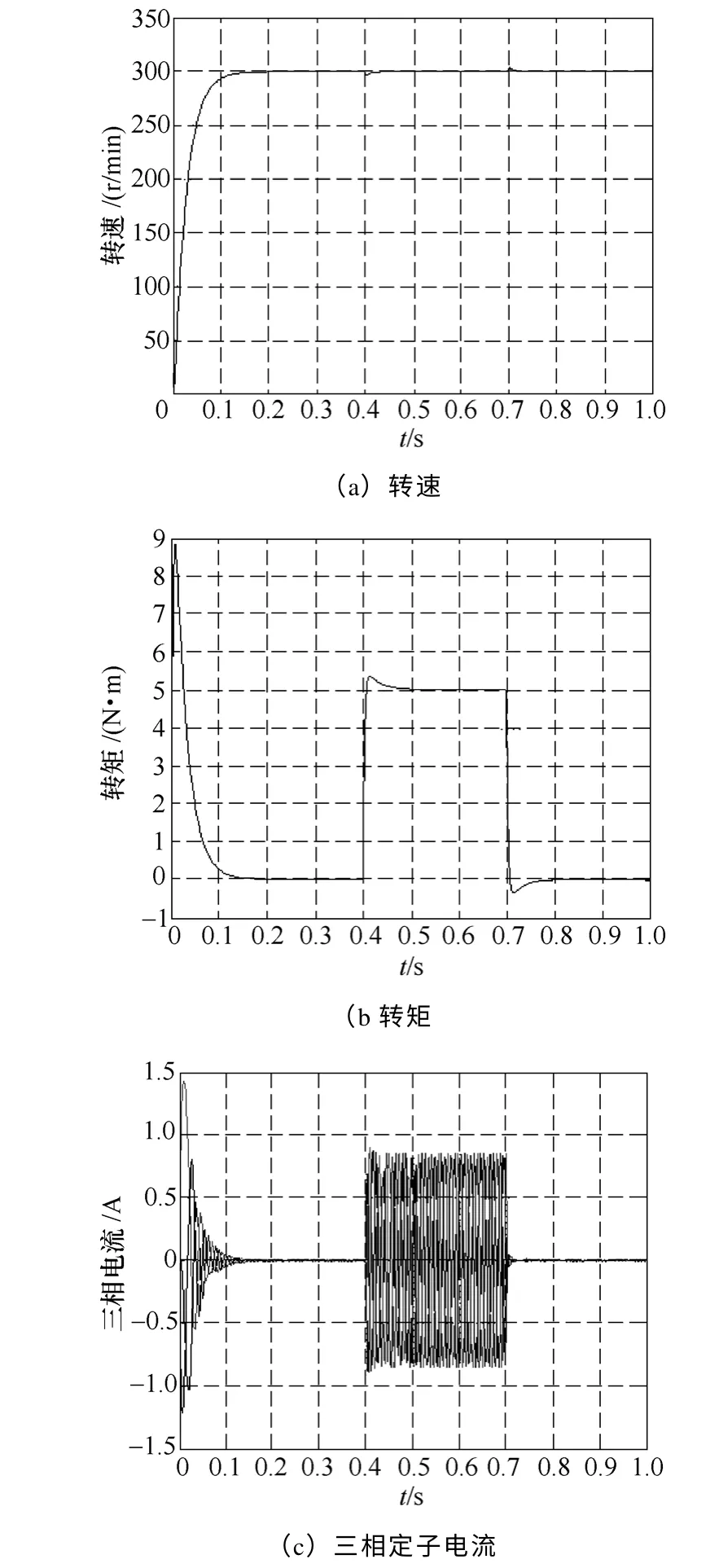
图6 模糊反推控制仿真结果Fig.6 Transient responses with fuzzy backstepping control by simulation

由仿真结果可以看出，当系统负载发生变化时，与反推控制策略相比，模糊反推控制策略通过模糊控制器对反推参数k、k1的实时调节，使速度的超调量与调整时间明显降低，三相电流波动减小，系统响应快速平稳。使系统具有快速的速度跟踪和抗干扰能力强的特性，动、静态性能都要优于反推控制。

4.2 实验结果

为了验证所提控制策略的有效性和可行性，在交流伺服系统的实验平台上进行了实验研究。实验系统采用TI 公司的TMS320F28034 芯片为核心，采用磁粉制动器给定电机负载，电机转速值通过D-A数模转换过来，并通过Tektronix TDS 2014B 示波器显示，实验装置如图7 所示。

图7 实验平台Fig.7 Experiment system

实验是通过系统负载变动，对采用反推控制和模糊反推控制两种控制策略的系统响应进行对比。图8 所示为无模糊控制的反推控制策略下的转速和定子电流波形，电机转速设定为300r/min，空载起动运行至稳定，实验中电动机首先突加5N·m 负载然后突卸5N·m 负载，图8a是转速波形，突加和突卸负载时转速波动值对应速度为12.4r/min，负载变动过程中转速出现最大误差为4.1%；图8b为此过程中三相电流波形，如图中标注圆，在突加负载和突卸负载过程中时有明显的波动。图9是相同实验条件下，采用模糊反推控制策略的速度和定子电流波形，图9a是转速波形，负载变动中转速最大波动值对应速度为3.9r/min，误差为1.3%；图9b为此过程中三相电流波形，如图中标注圆，在突加负载和突卸负载时没有明显波动。

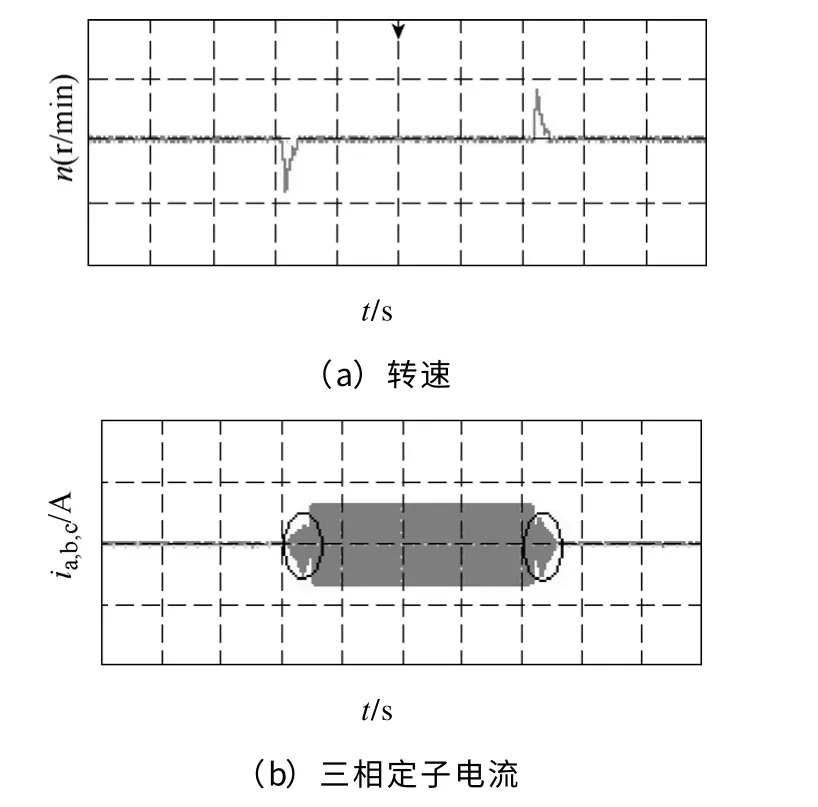
图8 无模糊反推控制实验结果Fig.8 Experimental results with backstepping control

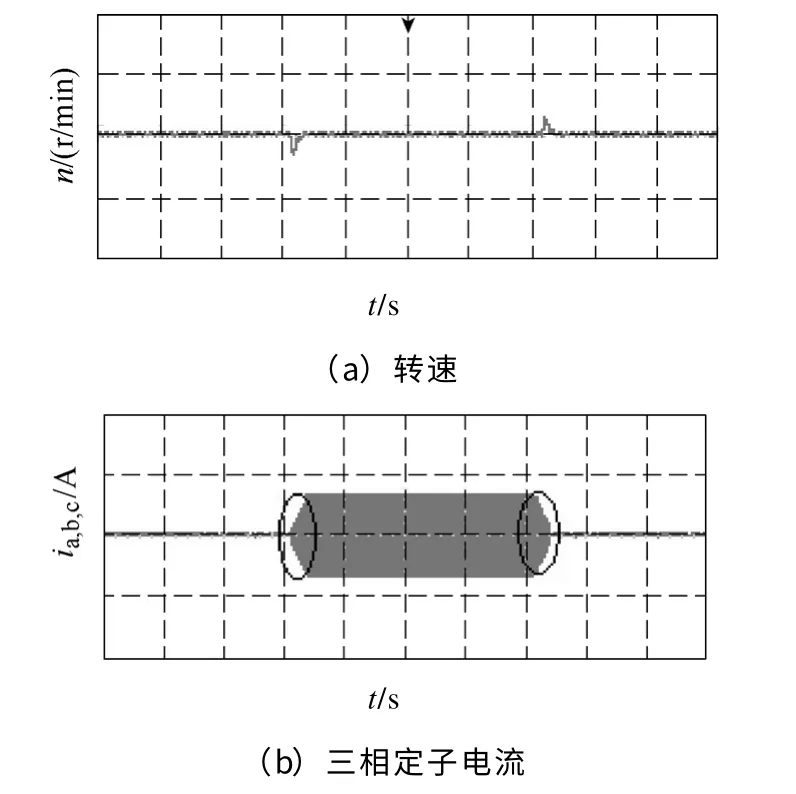
图9 模糊反推控制实验结果Fig.9 Experimental results with fuzzy backstepping control

由图8a 和图9a 可以看出，系统在两种控制策略下，当负载转矩发生变化时，选择模糊反推控制其转速波动小、调节时间短，速度跟踪效果更好，速度实验波形与仿真图5a、图6a 波形结果基本一致。由图8b 和图9b 可以看出，选择模糊反推控制在突加和突卸负载时，其电流变化平稳，基本没有调节过程，表明系统对转矩扰动有明显的抑制作用。

5 结论

本文把模糊控制和反推控制相结合应用于永磁同步电动机速度跟踪中。该方法通过模糊控制器对反推参数的在线调节，在保证系统全局渐近稳定的同时，实现了速度的快速跟踪性和较强的鲁棒性，使系统在动态和稳态时都能达到较高的控制精度。仿真和实验结果表明了该方法是有效性，把模糊反推控制应用于交流伺服系统中，能够实现良好的伺服性能。

[1]Baik I,Kin K,Youn M.Robust nonlinear speed control of PM synchronous motor using boundary layer integral sliding mode control technique[J].IEEE Transactions on Control Systems Technology,2000,8(1):47-54.

[2]张晓光,赵克,孙力,等.永磁同步电动机滑模变结构调速系统新型趋近率控制[J].中国电机工程学报,2011,31(24):77-82.Zhang Xiaoguang,Zhao Ke,Sun Li,et al.A PMSM sliding mode control system based on a novel reaching law[J].Proceedings of the CSEE,2011,31(24):77-82.

[3]任元,孙玉坤,刘叶飞,等.基于微分几何方法的永磁同步电动机变结构控制[J].微特电机,2006,34(11):33-35,39.Ren Yuan,Sun Yukun,Liu Yefei,et al.Variable structure control in permanent magnet synchronous motor based on the differential geometry method[J].Small &Special Electrical Machines,2006,34(11):33-35,39.

[4]Orgega R,Nicklasson P J,Espinosa G.Passivitybased control of the general rotating electrical machines[C].Proceedings of IEEE Conference on Decision and Control,1994:4018-4023.

[5]刘栋良,王家军,赵光宙,等.永磁同步电动机调速中的反推控制[J].电气传动,2005,35(6):39-41.Liu Dongliang,Wang Jiajun,Zhao Guangzhou,et al.Backstepping control and its application of PMSM[J].Electric Drive,2005,35(6):39-41.

[6]Hu Jianhui,Xu Yongxiang,Zou Jibin.Design and implementation of adaptive backstepping speed control for permanent magnet synchronous motor[C].Proceedings of the 6th World Congress on Intelligent Control and Automation,2006:2011-2015.

[7]王家军,王建中,马国进.感应电动机系统的变结构反推控制研究[J].中国电机工程学报,2007,27(6):35-38.Wang Jiajun,Wang Jianzhong,Ma Guojin.Variable structure control with backstepping of induction motor system[J].Proceedings of the CSEE,2007,27(6):35-38.

[8]刘栋良,郑谢辉,崔丽丽.无速度传感器永磁同步电机反推控制[J].电工技术学报,2011,26(9):67-72.Liu Dongliang,Zheng Xiehui,Cui Lili.Backstepping control of speed sensorless permanent magnet synchronous motor[J].Transactions of China Electrotechnical Society,2011,26(9):67-72.

[9]王家军,赵光宙,齐冬莲.反推式控制在永磁同步电动机速度跟踪控制中的应用[J].中国电机工程学报,2004,24(8):95-98.Wang Jiajun,Zhao Guangzhou,Qi Donglian.Speed tracking control of permanent magnet synchronous motor with backstepping[J].Proceedings of the CSEE,2004,24(8):95-98.

[10]高春能,纪志成.永磁同步电机的模型参考模糊自适应控制[J].系统仿真学报,2008,20(7):1817-1820.Gao Chunneng,Ji Zhicheng.Model reference fuzzy adaptive control of permanent magnet synchronous motor[J].Journal of System Simulation,2008,20(7):1817-1820.

[11]刘栋良,王家军,崔丽丽.永磁同步电机参数自适应调速控制[J].电工技术学报,2011,26(8):159-165.Liu Dongliang,Wang Jiajun,Cui Lili.Speed tracking control of permanent synchronous motors with adaptive parameters[J].Transactions of China Electrotechnical Society,2011,26(8):159-165.

[12]Pragasen Pillay,Krishnan R.Modeling of permanent magnet motor drives[J].IEEE Transactions on Industry Electronics,1988,35(4):537-541.

[13]Wang J J,Zhao G Z,Qiu J,et al.Position tracking control of permanent magnet synchronous motor servo system[C].Proceedings of the 5th World Congress on Intelligent Control and Automation,Hangzhou,2004:4512-4515.

[14]Sun Hua,Yuehong Dai.Fuzzy PID control and simulation experiment on permanent magnet linear synchronous motors[C].Electrical and Control Engineering,2010:1047-1049.

[15]Yu Junzhi,Hu Xiaolei,Ding Rui.Fuzzy logic PID based control design for permanent magnet synchronous motor servo system[J].Intelligent Computation Technology and Automation,2009,2(2):728-731.

[16]曾光齐,胡均安,王东,等.模糊控制理论与工程应用[M].武汉:华中科技大学出版社,2006.