挤塑聚苯乙烯泡沫板压缩强度控制研究

费梅花，恽 晨

（南京法宁格节能科技有限公司，江苏 南京211132）

0 前言

XPS泡沫板是以PS为主要加工原料生产的闭孔蜂窝结构的泡沫塑料，由于其具有极低吸水性、低导热系数、高抗压性、抗老化性等高性能指标，在2010年及2011年一度成为建筑行业的保温材料首选。XPS在美国发展了近70年才传入中国，虽然国内发展的15年时间，吸引了大量的资金，促进了国内XPS行业经历了蓬勃发展的十载历程，但由于大量投入的资本多用于购置生产设备、生产原料，而忽略了相配套的人才与技术的引入，导致行业内高水平技术几乎均掌控在外资企业手中。

目前，国内生产的XPS泡沫板已经广泛应用于墙体保温、铁路路基、公路路基、渠道河床等领域［1］。而国内关于XPS的理论研究多集中在阻燃技术、墙体保温系统中的应用等方面，对于生产过程的控制涉及较少，而在实际的生产过程中却常出现产品的压缩强度长时间浮动在订单要求的区间之外的现象，由此造成了生产的成本的大幅提高。

1 实验部分

1.1 主要原料

GPPS新料，535N，熔体流动速率3.7g／10min，维卡软化点温度为98.3℃，宁波台化塑料有限公司；

GPPS回收料，熔体流动速率6～30g／10min，市售；

成核剂，WF-101，江苏群鑫粉体材料有限公司；

氟利昂，R22／R1426（40／60混配），浙江蓝天环保氟材料有限公司；

液态CO2，南京吉恩化工有限公司。

1.2 主要设备及仪器

XPS泡沫板生产线，FS75T／200C，CO2生产线，1号机（双螺杆挤出机，螺杆直径为75mm，长径比32∶1），2号机（单螺杆挤出机，螺杆直径为200mm，长径比36∶1），南京法宁格节能科技有限公司。

2 基于多元线性回归的因素分析

2.1 建立多元回归方程

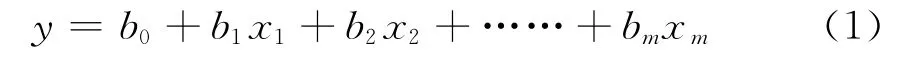
式中 y——因变量，A产品的下线抗压

b0、b1、…bm——常量及自变量的待定系数

xi——影响XPS泡沫板的最终抗压的可量化统计的自变量

本次测算待定系数采用最小二乘法确定，本文研究选用了7个预报因子，因此m＝7。

2.1.1 变量的选取与说明

XPS泡沫板内部为连续均匀的闭孔式蜂窝结构，其压缩强度主要由A产品的泡孔直径、泡孔密度、泡孔壁强度等3个因素决定［2］。泡孔直径主要由发泡剂量、二号机温度、热交换器温度、系统压力等决定，泡孔密度由成核剂量、发泡剂量、系统压力等决定，泡孔壁强度由PS的混合程度、PS的维卡软化温度等决定。本文在构建其压缩强度模型时，共选择分别影响XPS泡沫板泡孔直径、密度及泡孔壁强度等3大类共9个变量，如表1所示。

表1 影响XPS泡沫板压缩强度的变量说明Tab.1 Variable description of the compressive strength of XPS

2.1.2 数据的收集与整理

本文的研究数据来自实际生产统计数据，此处选取5cm厚度的XPS泡沫板生产数据作为研究对象。由于生产时的工艺参数是在各自配方产生的摩擦力及发热量实时调整的结果，导致配方不同，其投料量可能不同。为保证统计数据的可比性，将不同投料量下的工艺参数以500kg／h的投料量作为标准，先换算调整，以保证用于研究的数据在相同的投料量下进行回归研究。

2.2 模型的参数估计以及检验

2.2.1 模型的参数估计

对上述数据运用最小二乘法进行参数估计，通过SPSS 18.0统计软件对整理后的样本数据进行了多元线性回归，运算结果如表2所示。该模型拟合优度检验的可决系数R2＝0.824，修正的拟合可决系数R2＝0.805，这表明相关系数检验通过，说明此次选取的变量建立的线性回归模型能很好的解释该规格XPS泡沫板的压缩强度性能，拟合后的输出结果如表2所示。

根据表2可以确定上述多元线性回归方程为：

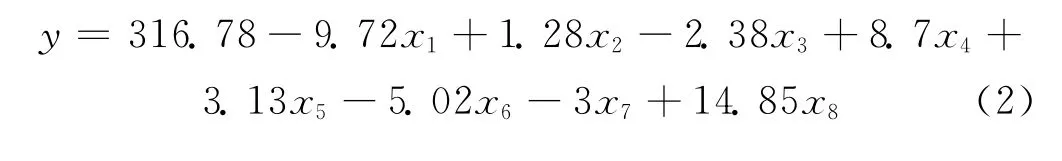
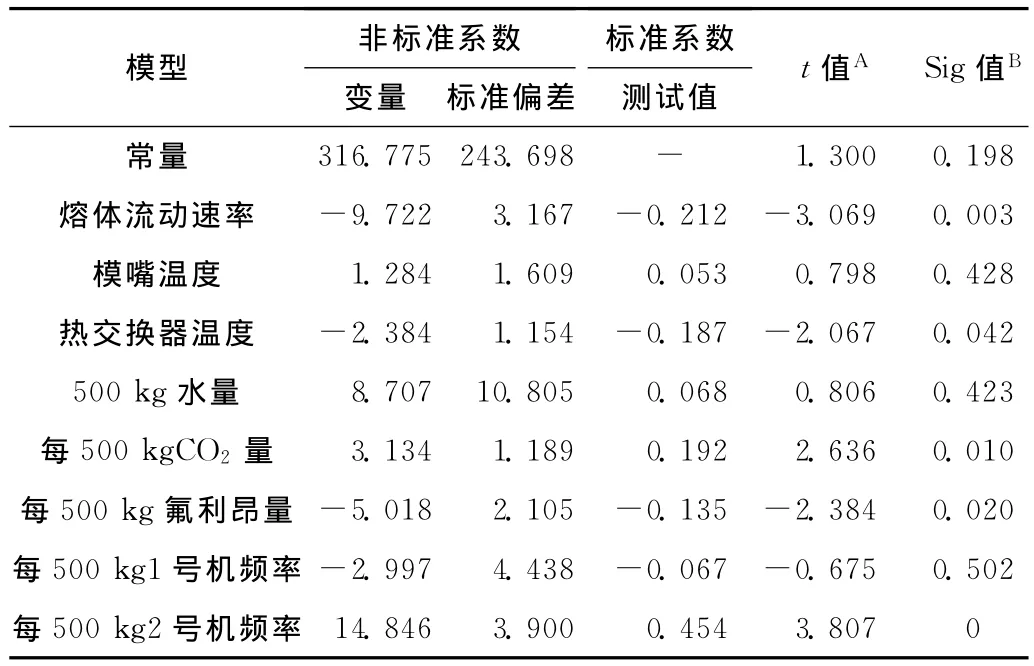
表2 线性回归系数表Tab.2 Coefficient of linear regression

2.2.2 回归模型的评估

为了验证1.2.1小节所建立的多元线性回归方程的可靠性，选取2012年7月份生产5cm厚的10组数据带入（2）式的回归方程中进行检验，获得如表3所示的结果。

在表3中，我们发现，编号1＃～5＃数据记录所预测的压缩强度值与实测的压缩强度值最大差值为31kPa，最小差值仅为0.5kPa，XPS泡沫板在生产过程中其压缩强度可浮动偏差为50kPa，可见预测的回归方程对新料比例在65%及以上的配方的XPS泡沫板抗压具有很好的指导和解释作用。但仍发现编号6＃～10＃中预测差值较大，主要是由于用于生产回收料的原材料品质各不相同，其相对分子质量相差较大，导致了其熔体流动速率在6～30g／10min这一较大范围内波动，但是每次生产前无法对每包回收料进行检测，导致记录的熔体流动速率与实际值有所偏差，对最终的预测结果影响较大。

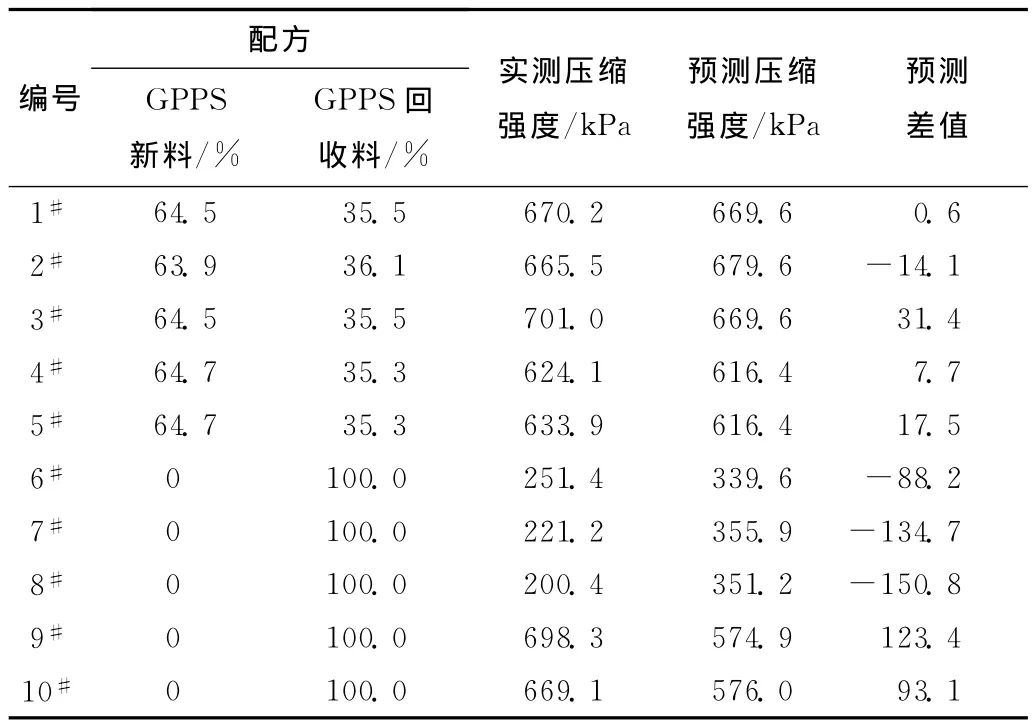
表3 验证回归方程可靠性Tab.2 Regression equation of the reliability

3 压缩强度预测系统

3.1 预测系统的运作流程

行业内大多数企业在生产前所做的工作即为准备原料、发泡剂、检查机器等，却不会在生产前计算该批次订单的工艺参数。由于挤出成型的特殊性，其生产是连续进行，每次开机机器升温需3h，开始投料到产品成型少则需要2h，多则4～5h，由于整个调试的过程均建立在操作人员的个人经验的基础上，其时间的长短一方面为设备原因导致，另一部分与操作人员理论水平有直接的关系。

由于前期没有确定相应订单所使用的工艺参数，即使在产品已经成型时，其物理性能很多时候也无法达到订单的要求，而实验室的物理性能检验还需要至少30min，在检验结果反馈至操作人员后，操作人员再继续调整工艺参数，接着实验室再检测，直至产品性能达到订单的要求，整个过程的长短与完全掌握在操作人员的经验丰富程度上，有时候由于其经验不足，其很多操作的调整反而是往所需要的相反方向调整。

笔者认为在掌握一定量的生产数据之后，完全可以在现有数据的基础上建立回归模型，对配方已经确定的订单使用多元线性回归模型进行压缩强度性能的预测，本小节继续以5cm厚度的XPS泡沫板的压缩强度为例进行仿真预测。

图1是压缩强度预测系统的运作流程，每一个流程都需要运行各自的程序代码来实现。

本系统是建立在SPSS软件对于原有生产数据回归模型的基础上实施预测。由于不同型号产品的系统压力、温度、主机频率、冷却水量等有较大差别，因此对不同型号产品分析时需进入“拟合系数设定系统”设置本次预测模型方程中的常数项及因变量系数。本次预测仿真基于实际生产，由于涉及商业机密的缘故，在预测结果输出中不包含调整方案。但是在实际生产中，应设定预测的期望值，系统输出预测结果时，应给出基于自变量对因变量的影响程度及因子间的对应关系而计算出的调整最佳方案。

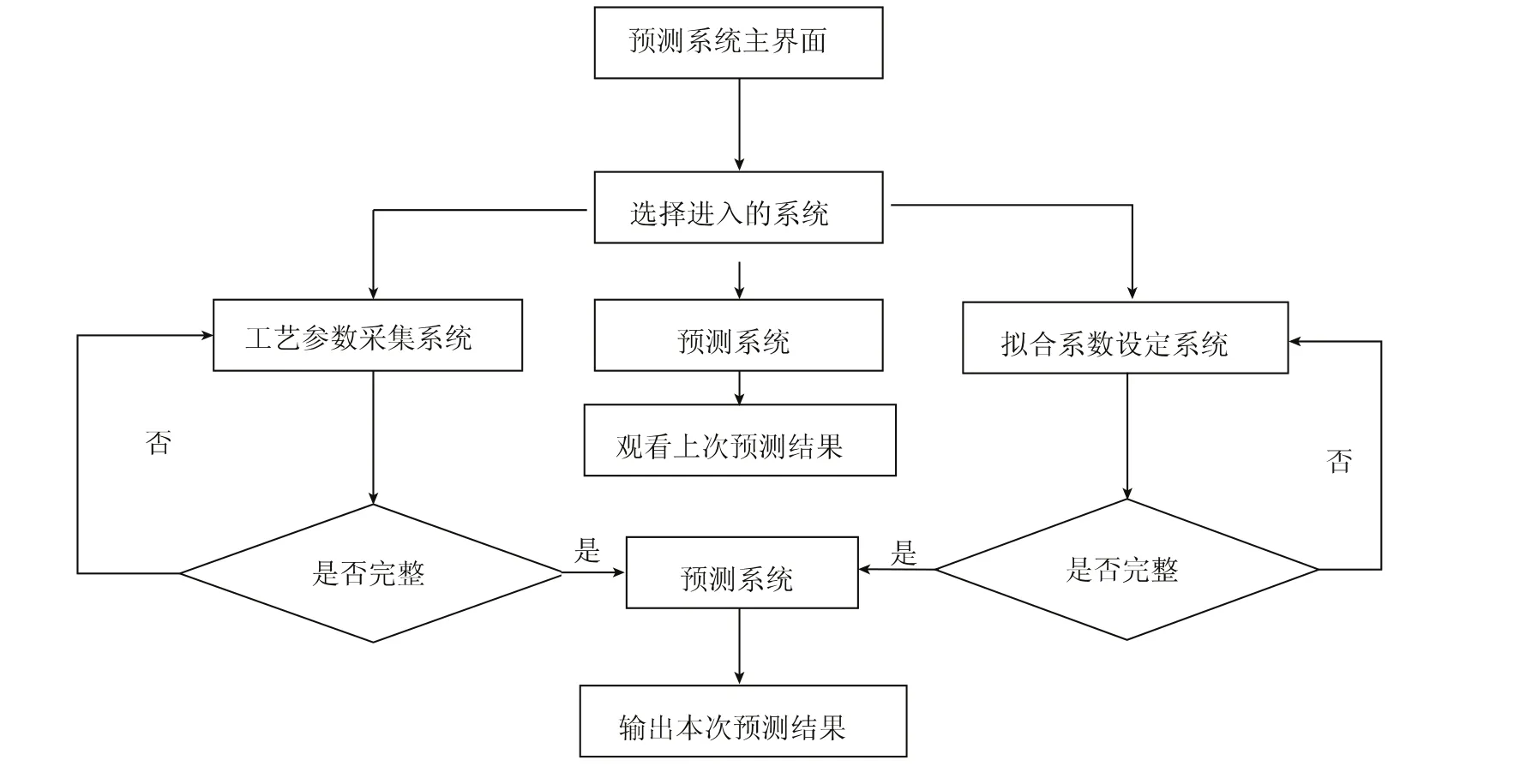
图1 预测模型运作流程Fig.1 Prediction model of the process

3.2 预测系统的实现与效果图

图2为预测系统的主界面，在主界面上分布“工艺参数录入系统”、“方程系数设定系统”及“压缩强度预测系统”，操作人员可以根据不同的需求，分别进入相应的系统内。“预测系统”读取的是数组a［i］［j］中的数据，即从主界面中直接进入时，显示的结果为上次工艺参数或预测模型下的输出结果，当新一组数据从录入系统进入时，预测系统读取数组a［i＋1］［j］中的数据。“方程系数设定系统”采用覆盖式的数据存储方式，即新方程系数输入时，前一个方程的系数值将被覆盖。

图2 压缩强度预测系统Fig.2 Compression strength prediction system

图3为工艺参数采集系统，在本节的仿真中选取熔指、热交换器温度、1号机频率、2号机频率、冷却水量、氟利昂量、CO2量等7个自变量Xi，预测因变量——压缩强度。此外，采集系统中还包括投料量信息的采集，主要是由于生产同一规格产品时由于投料量的不同，造成了工艺参数也有较大的差别。因此在后期的运算过程中，可根据投料量情况，先对工艺参数进行标准化，以减小预测的误差。

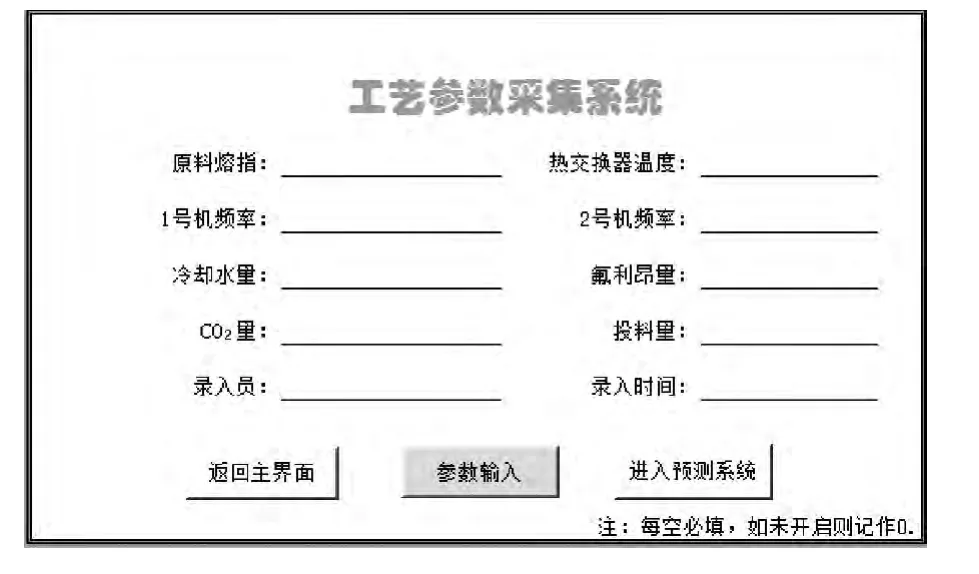
图3 工艺参数采集系统Fig.3 Process parameter acquisition system

图4拟合系数设定系统主要是针对变更不同型号产品时重新设定回归的方程设置，图中界面上的数据值是厚度为5cm的工艺数据回归后所得的常数项及自变量系数。在这里添置拟合系数设定系统主要是考虑到生产同一规格产品时由于气候、设备异常等原因造成工艺参数变化而需要对拟合的模型进行调整。工艺参数采集系统及拟合系数设定系统均采用If...then...函数［3］作为宏命令中的主体运算逻辑。

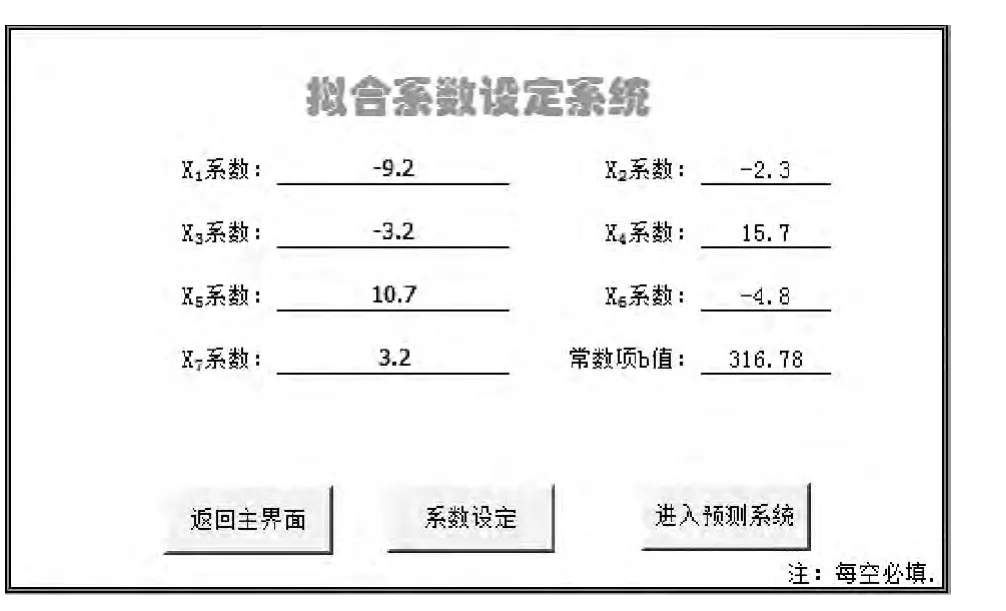
图4 拟合系数设定系统Fig.4 Fitting coefficient setting system

图5为预测系统进行运算后输出的弹窗，“预测系统”通过Sub JS（）宏命令进行触发，利用Range函数、赋值运算等方法调用数据库相应位置的数组值进行标准化运算，并将标准化值带入多元回归方程中求值，最后通过MsgBox函数，向系统外部输出结果。

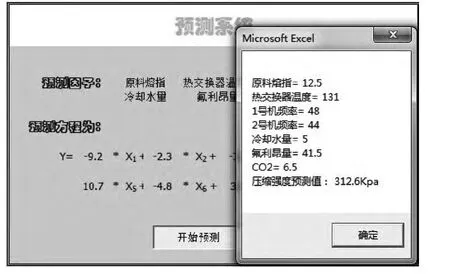
图5 预测结果图Fig.5 The prediction results

在使用该预测模型进行预测时，可先根据不同熔体流动速率的原料在料筒内的阻力值关系，计算投料量范围，再根据发泡剂与PS投料量之间较为稳定的比例关系，计算氟利昂及CO2注入量范围。依据同样的方式，先行确立将要运算的自变量范围，最后再带入该预测模型进行不断的调整。

4 结果与讨论

将多元回归引入挤出成型的生产过程，利用原有生产数据确立多元回归模型，并以拟合的多元回归模型为基础，搭建以Excel软件为平台的预测系统，设计压缩强度预测系统，使得在生产前可以根据订单要求对拟使用的PS原料的生产工艺参数进行测算，另一方面也可以引导开机手由口耳相传的师徒培养模式向科学的理论方向发展。根据表1中变量的预计方向与实际回归结果的偏差可知，仅凭借经验进行生产，有时造成的不仅仅是原材料的浪费，还会带来无头绪的产品品质控制问题。

4.1 参数估计结果评价

（1）2号机频率与压缩强度关系

从我们先期的理论角度对各自变量进行说明时，认为提高2号机频率将会增加螺杆与熔体的剪切热，因而会导致系统内熔体温度的上升，最终降低压缩强度。但是通过回归模型分析发现，1号机的频率与压缩强度呈正比例关系，从设备构造我们可以发现，由于2号机主要作用为冷却发泡，其桶壁包覆着冷却水套，循环冷却水在冷却水套中不停的循环以带走一部分热量，在提高螺杆转速时可以充分将熔体温度传递至桶壁以提高冷却水的作用，在这里我们可以得到这样的结论：冷却水带走的热量比螺杆频率提升产生的剪切热量要高。

（2）发泡剂（氟利昂）量与压缩强度关系

在生产过程中，我们通常认为增加发泡剂的注入量一方面可以降低熔体温度，另一方面可以提高系统压力，以提高产品的压缩强度。但是通过回归模型分析发现，氟利昂与压缩强度存在反比例关系，由于在生产时机器对当时使用原料的吃料量是有上限的，在PS量一定时，其氟利昂量也一定，每提高1Hz的注入频率，就将促使熔体内包覆的气体压力继续增加，当从模头释放出来时，熔体所面临的压力降越大，导致了成型后的泡孔也越大，泡孔壁也越薄。另外，由于气泡内压力过高，并泡现象将可能增加，这2个方面的原因均会造成产品的压缩强度下降。

从文中单独对分析结果和预测结果中与因变量相反比例关系的分析中我们可以发现，在产品的生产过程中，由于其受到多个因素的作用，且各因素可能会同时产生正反两种作用。只有在通过大量的数据记录与分析之后才能最终确定该因素对因变量的作用效果，而不能仅凭生产经验或者主观推断来进行生产。

4.2 预测系统总结

本文中Excel软件为平台使用VBA语言进行压缩强度预测的输入界面、数据库、数据分析、导出等的设计，使用该系统，可以对即将投入生产的已知原料的输出压缩强度性能进行预测，便于在生产前先行确定需要生产的工艺参数，为后期生产调整提供一定的参考。

虽然文中已经模拟XPS泡沫板的压缩强度指标的预测系统，但这只是初步的研究工作。挤出成型中需要考虑的因素很多，在后期的研究中应该进一步扩大思考的范围，充分考虑各方面的影响因素，在必要时应先做因子分析等工作，只有提高回归方程的可靠性，才能对生产做出其该有的正确预测和指导。其次在对特性指标进行预测时，还应根据预测期望和预测结果系统自动给出可供参考的修正的意见，理论服务于生产，希望在未来有更多的理论着眼于挤出成型的研究，将国内中小企业迫切需要的技术普及化，全面提高行业的过程品质控制能力及水平。

5 结论

（1）原料、工艺均影响XPS泡沫板压缩强度，其中2号机频率及发泡剂注入量为主要影响因素；

（2）通过SPS软件建立生产数据回归模型基础上对板材压缩强度进行预测，可得到较为准确地预测结果，也可为生产工艺调整提供参考，帮助企业提高生产过程控制。

［1］王 勇.中国挤塑聚苯乙烯泡沫塑料行业现状与发展趋势［J］.中国塑料，2010，24（4）：12-16.Wang Yong.Developing Situation and Trend of China XPS Foam Sector［J］.China Plastics，2010，24（4）：12-16.

［2］王向东，王 勇，郭鑫齐，等.挤塑聚苯乙烯泡沫塑料［M］.北京：化学工业出版社，2011，35-59.

［3］万星新，苏 玲.Visual Basic数据库开发全程指南［M］.北京：电子工业出版社，2008：1-21，225-324.