基于多层次模糊灰色耦合理论的高等级公路养护机械配置方案评价

李秀君， 李春龙， 李梦晨， 严 凌

（1.上海理工大学 环境与建筑学院，上海 200093；2.上海理工大学 管理学院，上海 200093）

高等级公路的养护作业质量、作业效率、经济效益主要取决于养护机械设备的合理配置，而这需要一个科学的配置方案评价方法来实现.一般来讲，高等级公路养护机械配置方案的选择应依据“适用、经济、环保”的原则.配置方案既要满足养护作业的要求，力求节约投资，取得最佳经济效益，同时又要达到质量与环保的要求［1］.并且，高等级公路养护机械配置方案评价问题中评价指标多，有些指标本身存在着不确定性和模糊性.因此，本文针对目前高等级公路养护机械设备配置方案评价的特点，在层次分析法的理论框架建立的基础上，将模糊数学与灰色系统理论相结合，旨在提出基于多层次模糊灰色耦合理论的高等级养护机械配置方案评价模型.该模型按照层次分析法结构将高等级养护机械配置方案评价模型分为4个层次，各层次指标因素运用频数统计法获得相应的权重.各层次指标因素中不确定型和确定型的指标采用不同的方法定量化处理，并将得到的处理结果按照灰色理论中的灰色关联分析法得到最后的总排序结果，该排序就是养护机械配置方案的优劣顺序.

国内学者在高等级公路养护机械配置方案评价方面进行了大量研究.梁平［2］利用层次分析和模糊综合评价的方法，建立了高速公路（沥青路面）养护机械配置方案的评估模型，对高速公路沥青路面养护机械配置进行了研究和探讨.马健萍等［1］运用灰色关联分析和层次分析相结合的方法，建立了高速公路（水泥砼路面）养护机械配置方案评价指标体系，提出了高速公路养护机械灰色关联评价比选模型，并在此基础上得出优选方案.吴永平［3］提出了机械化养护作业的技术经济评价模型：单位折算费用模型、成本效益计算模型和投资回收期计算模型，综合应用3种模型可以较全面地分析评价机械化养护方案的技术经济性.吴彪［4］采用一种基于相似度的决策方法，建立了高速公路养护机械设备配置方案评价指标体系，提出了养护机械设备配置方案综合评价模型.李文慧［5］运用层次分析方法，建立了高等级公路养护机械配置方案层次评价模型.

1 养护机械配置方案的评价指标体系

高等级公路养护机械配置方案评价过程是一个涉及到社会、技术、经济、环境等方面多目标多层次的过程，层次中指标间相互交叉或相互包含［6］.考虑到选取的指标必须具有系统性、可比性、可操作性，并避免指标之间的相关性，因此其方案评价方法属于多层次评价方法.按照层次分析理论中的层次结构，可将养护机械配置最为合理的配置方案放在最上层，通常称为目标层，一般只有一个因素；最下层通常为方案层；中间可有一个或多个层次，通常称为准则层［7］.因此本文以养护机械合理配置方案为目标层，以经济效益P1、社会效益P2、机械化程度P3为准则层，以及投资成本M11、作业安全M22和环境适应度M33等11个指标为指标层建立一个如图1所示的评价指标体系.

图1 养护机械配置方案的评价指标体系Fig.1 Evaluation index system of maintenance machinery configuration scheme

2 高等级公路养护机械配置方案评价模型

基于多层次模糊灰色耦合模型中选用灰色关联度法对高等级养护机械配置方案进行评价，该方法在小样本贫数据的情况下充分利用已有的白化信息，可以考虑到更多的因素，分析更为全面，减少评判误差.但是，灰色关联度易忽视指标之间存在的重要程度的差异［8］，因此，本文给评价体系中各指标因素赋予相应的权重.

2.1 层次指标权重的确定

在模糊决策中，权重反映了各个因素在综合决策过程中所起的作用，直接影响决策的结果，指标权重的确定在评价模型中占有重要的位置.因此，很多专家从不同角度运用不同的方法对权重进行了研究，通常有熵值法、层次分析法（AHP）、专家估测法和频数统计法等.熵值法和AHP 法所得结果较为客观，但计算复杂、工作量较大、可操作性差.专家估测法渗入专家的主观意识较多，难以保持权重的合理性.而频数统计法［9］为问卷调查形式，虽然也是依靠专家主观判断，但评价专家们可在不受外界干扰的情况下根据自身的经验和专业水平对指标进行评价，并对权重分配调查表进行数学处理，避免了专家评价的离散性，使获得的评价结果较为客观，可操作性强.故本文在确定评价指标的权重时采用频数统计法，专家应涉及高等级公路养护管理者、道路施工人员、道路养护理论研究人员以及机械方面的人员.

设因素集U＝｛u1，u2，…，uz｝，邀请q（q＝1，2，…，a；q≥30）位参与公路养护工作多年的管理、施工等方面相关专家，根据权重分配调研表对因素集U中各项因素各自独立地提出自己认为最合适的权重，根据收回的权重分配调查表，对每个因素ul（l＝1，2，…，z）进行单因素的权重统计分析，具体步骤如下：

a.对因素ul在它的权重ale（e＝1，2，…，q）中找出最大值Ml和最小值ml，即

c.计算落在每组内权重的频数ql与频率wl（l＝1，2，…，r）

d.则相应的准则层相对于目标层的权重WP和指标层相对于准则层的权重WM为

所得权重归一化运算为

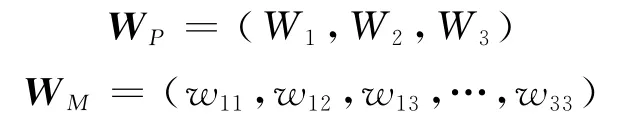
2.2 指标层中指标值的定量化与预处理（无量纲化）

影响目标层的因素中既有定量的又有定性的，因此可以把评价指标体系中的指标分为确定性和不确定性两种.对于确定性指标可用成本型指标（越小越好型）和效益型指标（越大越好型）表示；对于那些难以用数量表示的不确定性指标，利用模糊理论中的模糊语言定性描述指标，获得各个指标相对于每个方案的模糊隶属度评分.本文采用模糊数学方法中5级划分法［10］，即优、良、中、次、差5个等级，相应的隶属度为0.9，0.7，0.5，0.3，0.1.

计算值越小越好型的成本型指标和计算值越大越好型的效益型指标在采用线性变换的规范处理时所采用的基点不同，使变换后最好的效益目标和成本目标有不同的值，缺乏一致性，不便于比较［11］.可以采用数学变换来消除原始指标单位的影响，常用的方法有“功效系数法”、“标准化法”、“极值法”等.本文采用“标准化法”对各指标值进行预处理，把各指标值化为［0，1］区间内的数，以便于比较.

设养护机械评价体系由i个备选方案Ai（i＝1，2，…，n），j个评价指标Aij（j＝1，2，…，m）构成，则各备选方案的指标序列为Ai＝｛Ai1，Ai2，…，Aij，…，Aim｝.

对于成本型指标（越小越好型），即

对于效益型指标（越大越好型），即

式 中，Aj，max和Aj，min分 别 表 示 各 备 选 方 案 第j 项 指标的最大值和最小值.

2.3 灰色关联分析［12］

2.3.1 确定参考数列（又称母序列）与比较数列（又称子序列）

高等级公路养护机械配置方案的参考方案是理想状态下的理想方案，由于前文中各指标经规范化处理后，各指标值的最优值为1，所以参考方案中的指标序列作为参考数列可表示为X0（k）＝

高等级公路养护机械配置方案中各备选方案中的指标序列作为比较数列可表示为Xi（k）＝通过确定参考数据列X0（k）和比较数据列Xi（k）的几何形状相似程度来判断其联系是否紧密.曲线越接近，相应序列之间关联度就越大，反之就越小，反映曲线间的关联程度用关联系数εi表示.

2.3.2 指标层指标关联系数计算

根据灰色理论，参考数列X0（k）和比较数列Xi（k）在指标i处的关联系数为

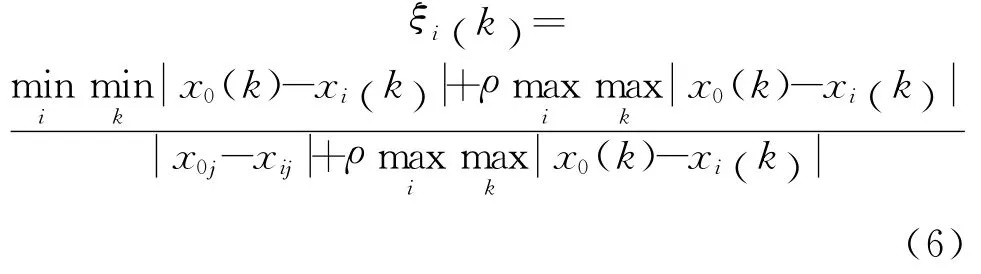
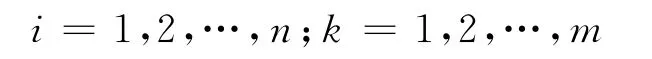
式中，ρ∈（0，∞），称为分辨系数.ρ 越小，分辨力越大，一般ρ的取值区间为（0，1），通常取值ρ＝0.5.

因参考方案指标序列的指标值均为1，故恒有

上式关联系数计算公式可改写为

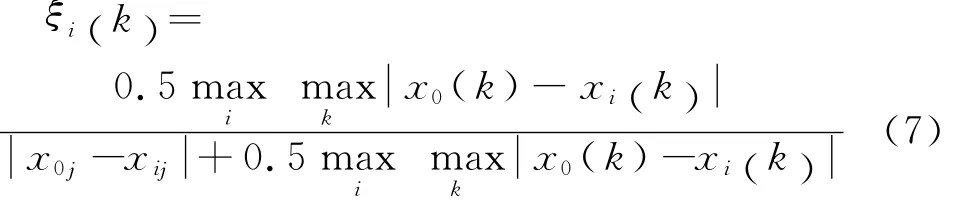
因此，可以得到隶属于准则层Pv（v＝1，2，…，s）某指标因素的指标层Mvj（j＝1，2，…，p）指标的关联系数矩阵为

2.3.3 准则层指标关联系数计算

指标层中各指标对相应准则层中因素的影响作用有所差别，所以在计算关联系数时应按照指标层中各指标重要程度赋予一定的权值.前文分析了指标层各指标隶属于准则层某指标因素的权重为WM，则准则层指标关联系数计算公式为

因为关联系数是参考数列X0（k）和比较数列Xi（k）在各个时刻（即曲线中的各点）的关联程度值，所以它的数不止一个，信息过于分散，不便于比较.为此有必要将各个时刻关联系数集中为一个值，求平均值便是作这种信息集中处理的一种方法，εi关联度公式为

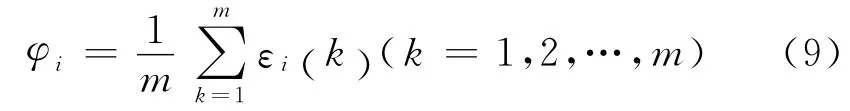
将进行了标准化处理的εi（k）整理，可得到准则层指标的关联度为

2.3.4 综合关联度计算

如前文分析所示，准则层相对于目标层的相对权向量为WP，则可得到准则层中各指标相对于目标层的综合关联度计算公式为

综合关联度反映了备选方案与参考方案的相似程度，备选方案与参考方案的两条曲线越接近，其综合关联度越大，反之越小.因此，综合关联度最大的备选方案为最佳方案.

3 实例分析

以某高速公路养护中心为例，该高速公路养护中心由于养护路段车流量增加而养护任务加重，根据该养护中心养护作业量及现有养护资金拟购置路面综合养护车、清扫车、洒水车、胶轮压路机.经过同一型号养护设备的综合比选，初步选定4个备选方案，本文将根据上文理论对其方案进行合理评价，最终选择出最优方案.

a.根据文中建立的评价指标体系，某高速公路养护中心在现有资金和养护作业量限定条件下由多位专家对各备选方案中单指标因素进行定量与定性的评价，可以得到备选方案各层指标的原始数据，结果见表1.

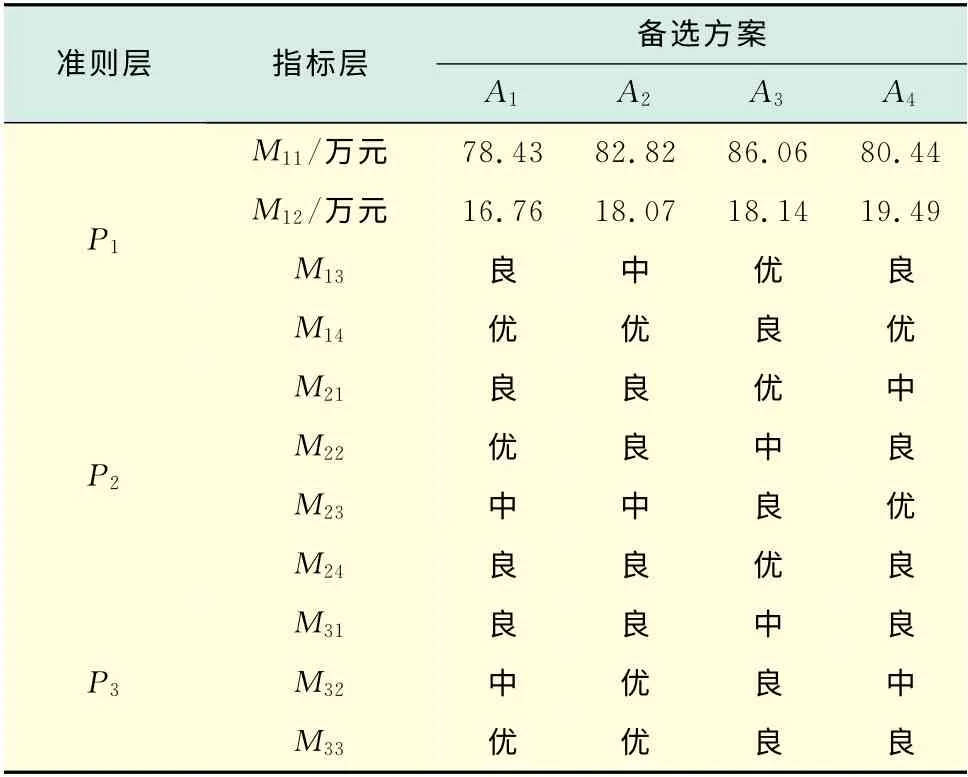
表1 养护机械设备配置方案各层指标原始数据Tab.1 Original data of maintenance machinery and equipment configuration index

b.原始数据的预处理.采用标准化法对表1数据无量纲化，邀请30位参与公路养护工作中管理、施工等方面的相关专家，采用频数统计确定评价体系中的指标权重，结果详见表2及表3.

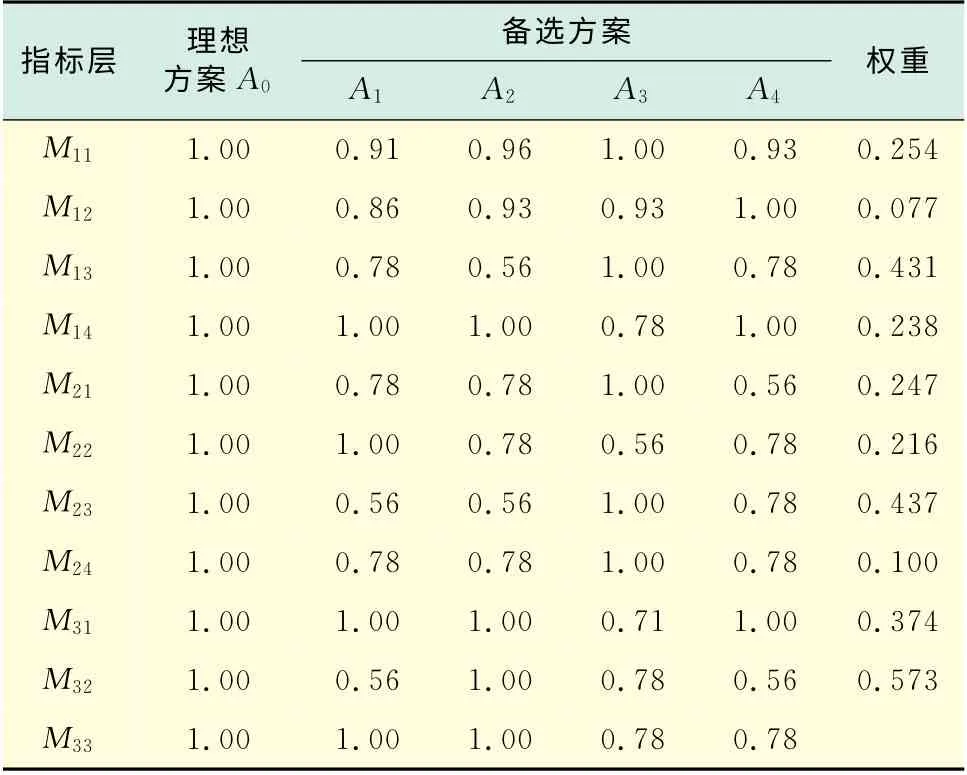
表2 指标层指标值预处理及权重Tab.2 Pretreatment of indicators and weightvalue

表3 准则层指标权重Tab.3 Weight value of criterion level

c.按照式（7），计算指标层的指标关联系数ξi（k），结果见表4.

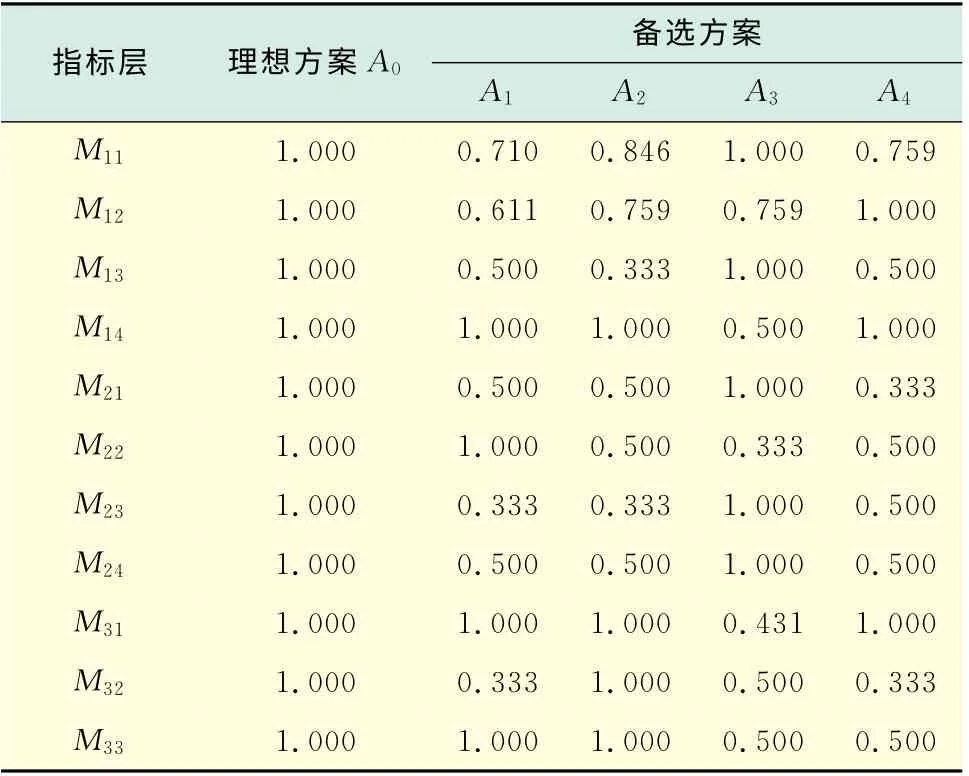
表4 指标层指标关联系数计算值Tab.4 Calculated value of index correlation coefficient of index layer

d.指标层关联度系数加权，即按照式（8）可得到准则层关联系数εi，将得到的准则层关联度系数εi按式（9）进行标准化处理得到准则层关联度φi，结果如表5及表6所示.

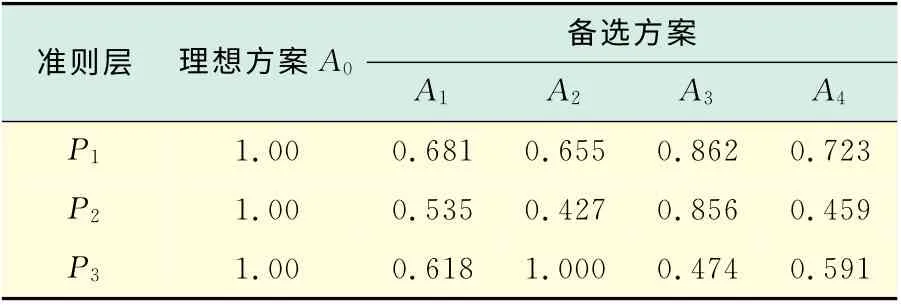
表5 准则层指标关联度计算值Tab.5 Calculeted value of index correlation coefficient of criterion level

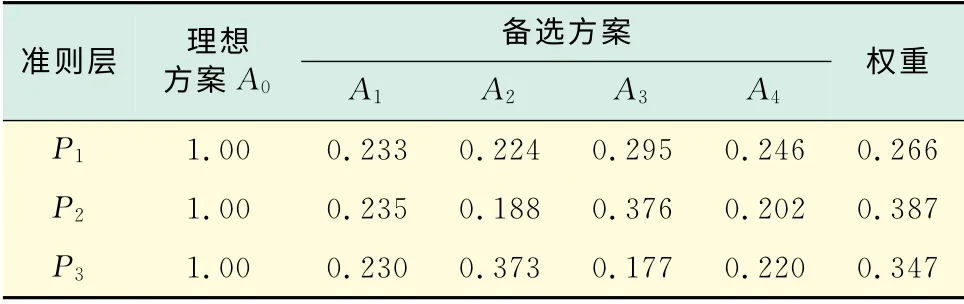
表6 准则层指标关联度（处理后）Tab.6 Index correlation coefficient of criterion level（processed）

e.计算综合关联度

综合关联度由准则层关联度加权得到，可按式（10）计算得到，其计算结果为

由上述计算结果0.285 401＞0.261 771＞0.232 733＞0.219 95可知，4个方案中优劣排序为γ3＞γ2＞γ1＞γ4，即最佳方案为方案3.这个实例与实际情况相符，说明了基于多层次模糊灰色耦合理论的高等级公路养护机械配置方案评价模型是可行的.

4 结 论

基于高速公路养护机械配置方案评价中影响因素的不确定性、模糊性，引入模糊灰色与层次分析思想，以实际调研数据为依托，客观真实地反映出各指标因素在方案评价中的影响作用.本文模型计算中，一个非常重要的环节就是对于权重的确定，采用频数统计法既避免了大量的计算工作又避免了主观的臆测.运用灰色理论中的综合关联度概念作为方案评价这一定性问题的量化标度，通过排列综合关联度大小顺序描述方案的优劣，概念清晰，利于比选.

［1］马健萍，何挺继，吕永雄.高速公路养护机械配置方案综合评估［J］.西安公路交通大学学报，2001，21（1）：99－102.

［2］梁平.高等级公路（沥青路面）养护机械合理配置方法研究［D］.西安：西安公路交通大学，1999.

［3］吴永平.机械化养护作业的技术经济评价模型［J］.长安大学学报（自然科学版），2002，22（5）：59－60.

［4］吴彪.高速公路沥青路面养护机械优化配置与评价体系的研究［D］.西安：长安大学，2004.

［5］李文慧.新疆高等级公路养护机械配置优化方案的研究［D］.新疆：新疆农业大学，2010.

［6］天津系统工程教研室.层次分析法［M］.北京：科学出版社，1986.

［7］杨平.基于模糊综合判断法的公路养护机械配置评价［J］.闽江学院学报，2011，32（2）：79－82.

［8］马超群，王玉萍，陈宽民，等.基于灰色加权关联度的城市轨道线网方案评价［J］.长安大学学报（自然科学版），2007，27（3）：84－87.

［9］谢季坚，刘承平.模糊数学方法及其应用［M］.3 版.武汉：武汉华中科技大学出版社，2006.

［10］王浙明，史惠祥，苏雨生，等.灰色关联模型用于工程方案优化［J］.中国给水排水，2002，18（1）：81－84.

［11］张跃，邹寿平.模糊数学方法及其应用［M］.北京：煤炭工业出版社，1992.

［12］邓聚龙.灰色系统理论教程［M］.武汉：华中理工大学出版社，1990.