基于贝叶斯方法的信息系统整合风险评估研究

袁光辉， 樊重俊， 熊红林， 冉祥来

（1.上海理工大学 管理学院，上海 200093；2.上海万达信息股份有限公司，上海 201112；3.上海机场（集团）有限公司，上海 201106）

贝叶斯方法提供了一种有效的风险预测手段，能够将主观估计与客观估计结合起来，并能随着资料的不断增加而不断进行预测，使得预测更加精确，有利于工程建设项目的动态风险管理［1］.

1988年，加利福尼亚大学计算机系Pearl给出了贝叶斯网络的严格定义并创建贝叶斯网络理论体系，近年来在各个领域都得到了广泛应用［2］.

针对软件项目的特点和软件项目风险定量评估任务，蒋国萍等［3］提出了基于面向对象的贝叶斯网络风险评估方法.该方法通过分析软件项目生命周期中的具体风险与风险因素之间的因果关系，建立面向对象的贝叶斯网络拓扑结构，由专家判断和工程经验确定网络中的概率参数，采用概率推断工具定量估计风险的发生概率.唐爱国等［4］采用贝叶斯网络推理软件项目失败风险发生的概率，用模糊语方评估风险后果与损失.袁健等［5］利用功能点模型和多元回归算法来进行软件项目工作量的预估，以降低对工作量估算的结果偏差，从而降低软件项目的风险.

张福生等［6］针对大型工程建设项目风险评估的实际需求，为对影响进度的风险作好预测，提出一种基于贝叶斯网络的工程项目风险评估模型及推理算法.算法在基于概率传播和更新的贝叶斯网络推理中，引入项目管理中分配给相应角色任务的最早开始时间、最晚结束时间等约束受限资源的风险评价概率因子.

唐爱国等［7］针对软件项目风险评估的应用需求，提出了基于贝叶斯网络方法的多种风险对某种风险后果的组合影响以及单个风险对整体后果的综合影响的度量模型，对软件项目中的风险进行了度量.

从上述研究中可以看出目前软件类的大多数风险研究集中在软件的实施过程及大型项目中的应用，信息系统整合方面的研究较少.由于信息整合特殊性的制约，软件项目的风险评估方法不能直接地在信息系统整合中进行使用.本文借助贝叶斯网络方法，结合信息系统整合的特殊性，对信息系统整合风险进行研究.最后结合算例，得出了在相同置信度情况下，本方法的置信区更为精确，这为决策者在风险评估决策时提供了更好的决策依据.

1 基于贝叶斯网络的信息系统整合风险分析

1.1 贝叶斯网络

贝叶斯网络是概率理论和图论相结合的产物，它是不确定知识表达和推理领域最有效的理论模型之一.贝叶斯网络由网络图结构和条件概率分布组成，Bs＝（V，E）是有向无环图，其中V 是节点集，E是有向边集，边表示节点与节点的依赖关系，依赖程度由条件概率决定.为了便于研究，将Bs细化为Bs＝（V，E，R），其中R 为网络中的关系.

根据贝叶斯网络，对于风险分析中网络中的一组变量X＝｛X1，X2，…，Xn｝，风险分析网络模型为一个二元组：Bn＝（Bs，Bp）.其中，Bp表示风险分析网络的条件概率分布表（CPT）集，任意变量Xi的条件概率分布为P（Xi｜$π（Xi）），其中π（Xi）是Xi的父节点集.另外，节点集V 中每个节点代表一个变量Xi，网络关系R 为产生的风险（后果）与风险因子（起因）的有序对.

风险分析网络中，各个节点关系无后向性，即符合马尔科夫条件（各节点后验结构只与其相邻的前一步结果有关）.其联合分布中的—般条目可使用风险网络节点的CPT 将分析网络中的概率信息计算出来.其中，CPT可以通过学习或者专家指定得到，则

由上式可以看出，X1，X2，…，Xn的联合概率分布的每个条目都可以用CPT 的乘积来表示.

1.2 信息系统整合风险的贝叶斯网络构建

对多个信息系统实现整合时，涉及的影响风险因子众多，用一组变量X＝｛X1，X2，…，Xn｝表示系统整合中的风险因子与产生的风险后果.根据因果关系建立二元有序对（Xi，Xj），其中Xi表示起因；Xj的先验概率为P （Xi），Xj表示后果.同时用带箭头的线将它们联结起来，箭头由Xi指向Xj，用P （Xj｜Xi）表示其联结强度.以此类推，最后可以建立信息系统整合风险的贝叶斯网络分析图与分析模型（见图1）.

图1 贝叶斯风险评估模型Fig.1 Bayesian risk assessment model

以信息系统整合的一些风险因子与风险后果为例作简要说明，组成后果模糊集，后果模糊集主要包含可预估的风险后果.从整合过程角度来分析，根据已有研究风险的理论和其它领域风险案例的成果，结合专家经验建立系统整合风险的贝叶斯网络评估模型［8－9］，如图2所示.将图2中的节点用变量Xi代替，可得到简化的系统整合风险贝叶斯网络图（见图3）.

图2 系统整合风险的贝叶斯网络图Fig.2 Bayesian network diagram of system integration risk

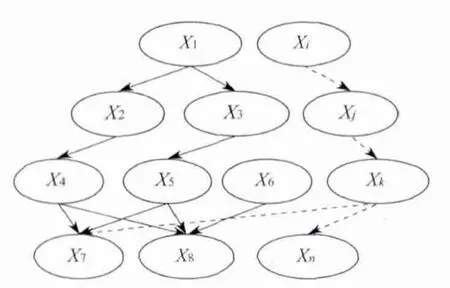
图3 简化系统整合风险的贝叶斯网络图Fig.3 Bayesian network diagram of simplified system integration risk

1.3 基于贝叶斯网络的风险评估

通过建立系统整合风险贝叶斯网络，从图3可知

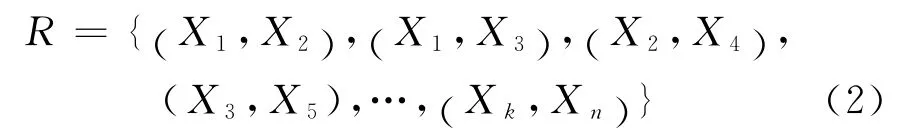
式中，R 表示贝叶斯网中各因素的直接关联结构.根据变量Xi特定的概率P（Xi）和CPT，可以利用贝叶斯网络中各变量的依赖关系，求其联合概率

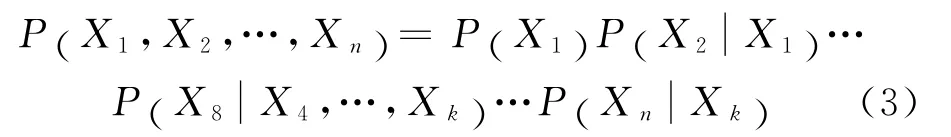
同理，根据风险贝叶斯分析网络结构进行推理，可得出各个风险节点的风险概率，记录每个风险节点的计算结果，以便进行下一步的推理计算，直到推理计算结束为止.

每次分析结束后，将相关数据存入特定的数据库中.随着进行风险分析的实际案例增多以及新信息的获得，历史数据和相关案例经验越来越多，在评估进行过程中，可实时进行网络的传播与更新，这样逐渐形成一个包含诸多独立风险模型的案例库，为以后模型的建立提供参考数据和经验.

2 贝叶斯方法在信息系统整合项目中的应用

2.1 贝叶斯方法的推广

设f（x）为随机变量的正态分布密度函数，μ 为x 的均值，x1，…，xn是x 的随机样本，已知精度ρ为方差σ2的倒数为样本均值.文献［3］根据贝叶斯原理，设x 是随机变量，其均值μ 也是随机变量.假设μ 的先验分布为正态分布，其均值μ′和精度ρ′已知，则μ 的后验分布也是一个正态分布，其均值μ″和精度ρ″分别为

由式（4）可以看出，后验均值μ″是先验均值μ′和样本均值x—的加权平均值，其权重是由ρ′和nρ 决定的；由式（5）可以看出，ρ″与样本观测值xi无关，随着观测次数的增加，μ 的后验分布越来越集中于后验均值的附近，而其均值将取决于观测值xi.

信息系统整合项目比单一的信息系统开发项目要复杂得多，因为系统整合牵涉的用户（user）、用户界面（user interface）、业务逻辑（business logic）、数据服务（data service）众多，而不是单一的，所以在实施系统整合的时候需要考虑的因素也就颇多，毋庸置疑，带来的风险也不容忽视.实际上，只要对风险评估得当，采取有效措施，都可以将风险控制在可以接受的范围内.

任何项目，不管涉及的风险因子有多少，最终都离不开工期、成本（支出费用）、系统整合后的总体性能这三大因子的风险困扰.对于风险分析可实施全方位风险分析计算，亦可对以上3个因素单独分析.

2.2 以成本为例进行风险分析建模

根据数据的可得性及一个具体的信息系统整合项目，成本是业主和集成商直接且首要考虑的因素，下面以信息系统整合成本因素为例，利用贝叶斯方法进行风险评估分析.

以一定时间为单位（周、月、年）构成估计成本序列，考察其预计费用与支出情况以及费用超支与否的次数，建立模型推导费用支出概率分布.系统在设计开发过程中，需要不断和用户沟通，需求可能不断发生变更，产生的费用xi是个随机变量.由于影响因素众多，可以认为xi是个均匀分布的随机变量，那么x1＋x2＋…＋xn的极限分布是正态分布，其均值为μ′，方差为δ2.根据数据确定参数，计算出单位时期的成本预算.

根据贝叶斯方法原理，信息系统整合项目成本支出风险分析步骤如下：

步骤1 统计分析源数据，即采样分析历史数据，计算样本均值x—、方差S2、精度ρ.

步骤2 确定先验概率分布，这个过程中可以让项目组成员（或者行业专家）根据历史经验，主观初步估计成本预算，然后将所得的估计值按权重得到平均值，并计算误差范围，这样就得到了先验的概率分布参数μ1 和精度ρ1.

步骤3 根据先验概率分布，进行后验概率分布推断.

步骤4 拟定置信度1－α，查正态分布表得到uα，则支付费用均值μ′的区间估计可以获得.

步骤5 继续补充新信息，应用上述分析步骤，随着信息量的增加，估计值就越来越趋于实际值.

2.3 实例分析

某公司为信息系统行业的开发商兼集成商，作为集成商根据用户和业务实际需求，对相关信息系统进行整合.在和用户进行沟通交流后，了解了用户的整合需求，同时也得知开发或者整合的风险.在实际系统整合的风险当中，成本和进度风险是考虑的重要对象.现以该公司2010年实施信息系统整合项目的月支付费用中连续10个月的数据为实例进行分析.

该公司事业部在实施某单位的信息系统整合项目时，其中10个月的支出（不包括硬件设备的采购支出）见表1.在项目实施前，为了减少中标后带来的项目成本风险，项目组核心成员对支出费用进行了大致估算，见表2.

表1 某系统整合项目中连续10个月的支出费用Tab.1 Expense in successive ten months of some row in a system integration project

a.根据已知样本计算均值、方差、标准差、精度

表2 某系统整合项目估计月支出费用Tab.2 Estimated monthly expense of some integration system project

b.预算先验均值、方差、标准差、精度

先验标准方差S′＝5.244

先验精度ρ′＝0.036 4

c.后验概率分布推测

d.令α＝0.01，置信度为1－α＝99%，uα＝2.58，则预计支出均值μ 的置信区间为

支出预算落入（34.188，36.798）的可能性是99%.在实际应用中，置信度可以根据需要取值，实际置信度不一定能达到99%，可以根据经验拟定置信度.

e.相似的信息系统整合项目费用支出信息见表3，用于费用风险推理.

根据贝叶斯学习理论，原有的后验信息变为先验信息，根据新增加的信息再次进行后验推测.

表3 项目预算估计Tab.3 Project budget estimate

令α＝0.01，置信度为1－α，uα＝2.58，则预计支出均值μ 的置信区间为（34.315，35.905）.

通过计算发现，通过相似项目信息学习后的计算结果较无相似信息学习的计算结果效果更优.即在置信度相同的情况下，有学习结果在支出估计区间范围较无学习结果有所减小，也就是说置信区间更为集中，估计更接近实际，有利于决策.

由以上实例分析可知，对于信息系统整合项目，可根据已有相关项目确切的数据统计或具有丰富经验的行业专家分析的数据统计，利用本文方法对正在实施的项目进行风险量化评估，以达到发现风险的目的，从而降低施工企业的潜在风险，降低项目施工延期风险，这对施工方及客户均具有实际的价值和意义.显然利用贝叶斯方法评估信息系统整合项目风险损失具有一定优势.

3 结束语

分析了贝叶斯方法理论，基于贝叶斯方法对信息系统整合项目风险评估模型构建整合风险贝叶斯网络图，并根据先验概率或者专家经验，实现对未知风险的量化计算.同时，进行了实际案例推算，计算结果可供决策者进行参考分析.随着添加的历史信息的增多与经验的累积，估算越接近实际值，这样能让决策者在评估风险时减少失误和降低损失.从分析的结果可发现，本方法不仅可在信息系统整合中得到使用，同时可在施工项目的风险评估中使用.

［1］贾焕军.贝叶斯方法在工程建设项目风险分析中的应用［J］.数理统计与管理，2005，24（3）：10－14.

［2］冀俊忠，刘椿年，沙志强.贝叶斯网模型的学习、推理和应用［J］.计算机工程与应用，2003，39（5）：24－27.

［3］蒋国萍，陈英武.基于面向对象贝叶斯网络的软件项目风险评估［J］.系统工程与电子技术，2005，27（2）：353－356.

［4］唐爱国，王如龙.基于贝叶斯网络的软件项目风险评估模型［J］.计算机工程，2008，34（22）：91－93.

［5］袁健，丁岳伟，李海渊.软件项目工作量预估系统的研究与实现［J］.上海理工大学学报，2005，27（6）：547－550.

［6］张福生，王洪泊，杨扬，等.一种基于贝叶斯网络的建设项目风险评估方法［J］.计算机仿真，2010，27（7）：296－298.

［7］唐爱国，王如龙，胡春华.贝叶斯网络在软件项目风险评估中的应用［J］.计算机工程与应用，2010，46（7）：62－67.

［8］王桢珍，姜欣，武小悦，等.信息安全风险概率计算的贝叶斯网络模型［J］.电子学报，2010，38（S1）：18－22.

［9］樊重俊，熊红林，张海英，等.虹桥机场信息化建设项目中的风险管理方法［J］.科技管理研究，2010，30（8）：129－132.