一种新的原子结构模型及其计算机演示
2014-11-22吴国玢FHERRMANN章琢之
吴国玢, FHERRMANN, 章琢之
(1.上海理工大学 能源与动力工程学院,上海 200093;2.卡尔斯鲁厄理工学院 物理系,卡尔斯鲁厄 76128;3.上海教育出版社,上海 200031)
模型是描述、研究和解释物理现象或物理过程的基本方法之一.模型可以帮助人们了解并掌握那些他们难以直接体验或者无法通过直觉认知的物理现象或过程.显然,模型应该是一种人们已经熟悉(最好直接来自日常经验)的因而加以信赖的系统.模型一般不可能也不必要与实际的物理系统处处相似.通常,一个模型只要能够在一定程度上或者部分地为人们描述某个物理系统提供某种方便,那么它就是一种有用的模型.本文作者认为,一个模型是否有效还应看它是否具有某种可操作性(operability),能否用来解决一些实际问题;换言之,一个好的模型不仅应该具有描述或展示的功能,还应该能够以人们所熟悉的方式对它进行操作,以得出一些与事实相符的有用结果或结论.
目前国内外各种物理教科书和科技文献中常用的原子模型理论为:原子由带正电的小而重的原子核和带负电的大而轻的原子壳层所组成.原子壳层则由围绕原子核运动的电子云或点状的粒子电子组成,但电子的位置是不确定的,人们只能给出电子在某一时刻某一空间点附近单位体积内出现的概率.电子虽然绕原子核运动,但并无确定的运行轨道.这种模型与人们的日常经验相去甚远,因为人们从未见过这种既没有确定位置又没有运行轨道的奇特运动物体.不过主要问题还不在于此,而是在于它的可操作性不强,或者说人们不知道应当如何去有效地操作或运用这个模型来说明或解决一些实际问题.本文提出一种基于薛定谔方程的解——波函数的新模型,以试图改善上述状况.
1 电子素模型的建立
以下单电子系统的薛定谔方程是本文讨论的出发点
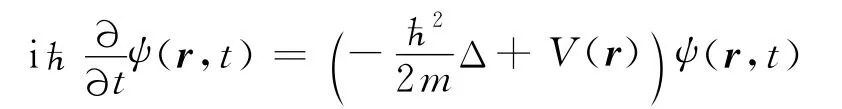
式中,ħ 为普朗克常量;m 为电子质量;V(r)为势函数;r和t分别为电子的空间坐标矢量和时间.现在用波函数ψ(r,t),即薛定谔方程的解来定义以下两个量ρ 和j,即
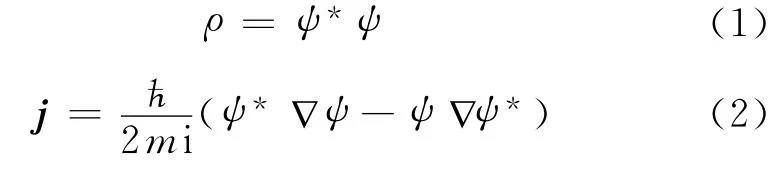
式中,ψ*表示ψ(r,t)的共轭函数.根据上述定义和薛定谔方程,经简单运算后得到[1]
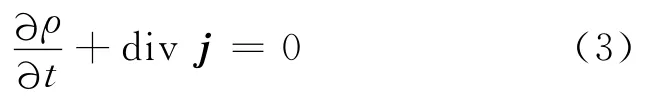
此式具有连续性方程的形式.将上述两个量ρ 和j分别乘以电子电荷e和电子质量m,便可得到
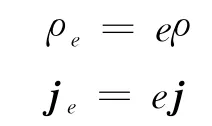
以及
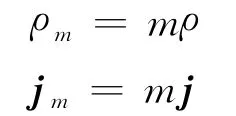
根据式(3),可以立即写出以下两个连续性方程
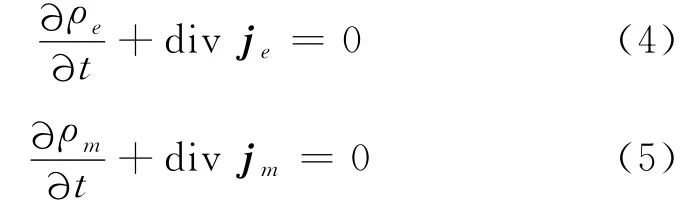
不难看出,式(4)表述了原子壳层内的电荷守恒,式(5)则表述了原子壳层内的质量守恒.这样,人们就有依据将原子壳层想象成是一种由连续地分布在原子核周围的带电流动物质所组成的.这两个方程的具体含义是,若在给定空间内的电荷或质量减少,那么必然有等量的电荷或质量从该空间中流出;反之,若该空间内的电荷或质量增加,则必然有等量的电荷或质量从外界流入该空间.由于在随后的讨论中经常会提及这种想象的“物质”,因此不妨为它起一个专门的名字:电子素(electronium).这样,ρ就是电子素的密度,而j则是电子素的流密度.由于电子素密度的数值取决于波函数,因而它会随着空间位置和时间的变化而变化.在原子核附近,电子素密度最大,距离原子核越远,密度就越小,并无明显边界.为便于表示原子的大小,通常取覆盖90%电子素的半径为原子半径.既然电子是由电子素所组成的,那么电子素这一物质就不能任意连续分割,而是一份一份,有其基本单元的.这个基本单元或粒子实际上就是电子,其质量就是电子质量(10-30kg),其电荷就是电子电荷(-1.6×10-19C).显然,电子素只能以其基本单元(电子)的整倍数离开或进入原子壳层.换句话说,电子素是一种量子化的物质.
2 用电子素模型表示各种原子状态
下面接着来考察一下与各种不同的薛定谔方程的解所对应的电子素密度ρ的分布状况,即原子所处的状态.众所周知,薛定谔方程具有特解
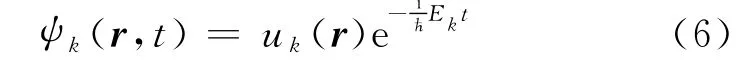
与其各种解所对应的各种粒子状态称为能量本征态.它们用下标k进行编号.每一种解对应于一个特定的能量值Ek,称为能量本征值.容易看出,式(6)中的第一个因子uk(r)只与位置r有关,而第二部分则仅与时间t 有关,也就是说,它们是相互分离的.将它们代入式(1),立即得到处于本征态下的电子素密度表达式
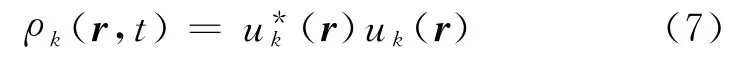
此式表明,由于指数项的乘积为1,电子素密度在本征态下只与位置有关而与时间无关.类似地,电子素流密度在本征态下也与时间无关(但不必为零).这就是为什么本征态也可以称作定态的缘故.利用关系式ρ=ψ*ψ 通过计算,便可绘制出在不同能量本征态下电子素密度分布的二维或三维图形.图1所示为氢原子在各种不同定态(基态和激发态)下的电子素密度,图中,n 为主量子数,s,p,d,f,g则为副量子数l所对应的光谱符号.其中,图1(a)所表示的是电子素密度分布的二维剖面;图1(b)是其中一个定态(210)下电子素密度分布的三维示意图.红色区域为电子素密度最大之处,蓝色则表示密度最小,而黄色所表示的是电子素密度为零的各种表面(节面).上述图形实际上已为大家所熟悉,可见电子素模型同样可以用来形象地表述原子所处的各种状态.
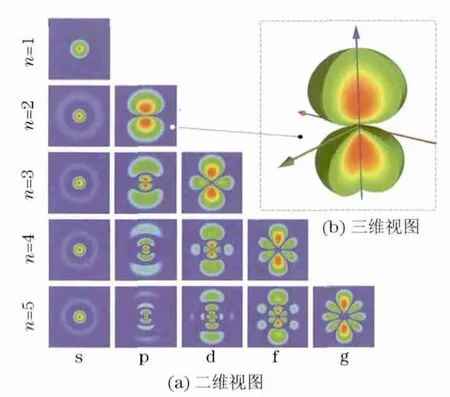
图1 各种定态(m=0)下氢原子内的电子素密度分布Fig.1 Electronium density of hydrogen atom in various states(m=0)
下面进一步讨论所谓的叠加态.由于薛定谔方程是一个线性微分方程,因此作为它的解的波函数满足叠加原理.这就是说,该方程各本征态解的任何线性组合
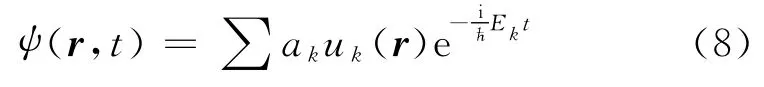
都满足薛定谔方程(其中ak可为任意常数).与之对应的粒子状态所以可称为叠加态.下面讨论一种最简单的叠加态,即由两个本征函数之和所组成的波函数,即
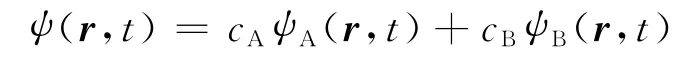
式中,cA和cB为常数系数.将此式代入电子素密度的定义式(1),由于此时各波函数中含有时间变量的指数部分不能相互抵消为零,最后得到的电子素密度具有形式
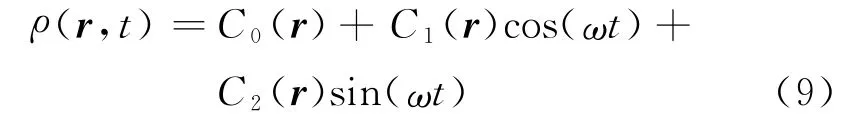
式中,C0,C1和C2分别表示仅与空间位置r有关的项,各个三角函数项则仅与时间t 有关,其中ω=(EA-EB)/ħ,EA和EB分别为两种本征态下的能量本征值.
很明显,电子素密度ρ 在叠加态下与时间有关,即随时间而变化.它由一个只与位置有关的项及其它随时间作简谐振荡的项所组成.流密度j 的情况与此类似.由于叠加态与时间有关,因而也称为非定态.具备了关于电子素的基本知识之后,下面就可以通过几个具体例子来说明如何运用或操作电子素模型.
3 电子素模型的实际应用
3.1 原子的形状
能量本征态通常用3个量子数n,l,m 加以表征.图2所示为氢原子在n=4,l=3以及m=1状态下的电子素密度分布.根据新模型,现在可以将ρ=ψ*ψ 当成是一种分布在原子壳层内的具体物质的密度,而不必抽象地或令人费解地将之解释为电子在某空间内出现的概率的密度.这样,这个图形也就可以顺理成章地理解为原子形状的形象化表述,即直接而且直观地反映出原子的形状.

图2 量子数为n=4,l=3和m=1状态下的氢原子形状Fig.2 Electronium density of hydrogen atom in the state n=4,l=3and m=1
3.2 原子的角动量和磁矩
在m≠0的状态下,电子素围绕着经过原子核的轴线做旋转运动,所有圆形流线(闭合的圆周线)均位于垂直于旋转轴的平行平面内.于是,在原子壳层内同时存在着两种流动:质量流和电荷流.前者具有角动量(angular momentum);后者则表明原子具有磁矩(magnetic moment).就这样,即便运用经典力学和电磁学的概念就能对轨道角动量和磁矩给出令人信服的解释.更进一步,角动量和磁矩的数值也可以运用电子素模型计算出来,所得结果与根据量子力学本征值方程的计算结果相互吻合.图3中的箭头指示出原子中电子素的流动方向.流动方向可以由定义式(2)加以确定,也可以在实验中根据磁矩的方向来确定.

图3 定态(431)下氢原子的电子素密度分布及其流动示意图Fig.3 Electronium density and current of hydrogen atom in the stationary state(431)
3.3 定态下的原子不发生辐射
根据式(7)和前面关于原子定态的讨论,已知道在定态下的电子素密度ρ的分布和流密度j 的分布都只与空间位置有关,而与时间无关,即不随时间而变.电荷分布不随时间而变,意味着它所产生的电场是一个静电场;电流分布也不随时间而变(稳恒电流),则意味着它所激发的磁场也必然是静磁场,不会辐射电磁波,尽管电子素流动本身存在着加速度.由此不难理解,处于定态的原子不会发生任何电磁辐射.实际上从图3 也可以直接得出同样的结论.
大家知道,处于定态的原子不发生电磁辐射是与当时的经典电磁理论相抵触的,因此玻尔提出了经典电磁理论在原子结构中不适用的假设,建立了他的量子轨道模型.玻尔的理论首次打开了人们认识原子结构的大门,取得了很大成功,但是也存在一定的局限性,比如未能给出上述不适用的充分理由.然而,利用电子素模型进行解释,简单明了、令人信服,学生比较容易掌握.
3.4 电子跃迁
电子素模型的另一精彩之处在于它对电子跃迁的描述.要描述电子从一个定态向另一个定态的跃迁只需利用前面讨论的关于叠加态的知识,将相应的初态和终态波函数进行叠加就可以了.电子素密度在电子跃迁过程中随时间的变化可以用前面的公式(9)进行计算,其振荡频率ω=(EA-EB)/ħ,其中EA和EB分别为初态和终态下的能量本征值.这样就可以制作出从一个定态跃迁到另一定态的动画视频,以对电子素密度的振荡进行动态演示.一个典型的跃迁大约持续10-8s.在此期间,电子素密度的振荡次数在107左右.为了使整个跃迁过程能够用肉眼观察,作者采用了一种“频闪(stroboscopic)”技术,将跃迁过程的动画演示由时间间隔比实际间隔长得多的一系列画面所组成.这样,振荡频率可减低到似乎整个跃迁过程只发生十几次或几十次的程度,适合于人们观看.虽然动画无法用书面形式表达,但人们可以从中截取部分图形加以展示.图4所示为氢原子从定态(210)跃迁至定态(100)连续过程的示意图.
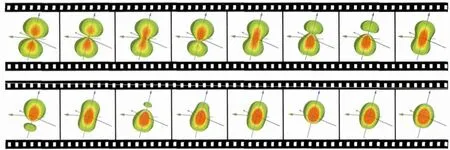
图4 电子素的振荡:氢原子从一个定态(210)跃迁至另一定态(100)Fig.4 Electronium oscillation:the transition of hydrogen atom from state(210)to state(100)
网 站www.physikdidaktik.uni-karlsruhe.de为广大读者提供了一批氢原子跃迁过程的动画短片视频,欢迎观看或下载.
4 历史的回顾
众所周知,爱因斯坦对波函数的概率或统计解释始终不予认同,而且实际上一直持批评态度.他的名言是:“上帝不玩掷骰子的游戏”.电子素模型将波函数抽象的统计概念(概率密度)解释为一种可流动的具体物质的密度,因而能够在一定程度上缓解爱因斯坦的质疑或他与哥本哈根学派之间的争议.
1913年,玻尔以他特有的睿智方式所提出的假设,有效地解决了处于定态的原子不向外辐射能量与经典电磁理论之间的矛盾.整整100年之后,本文又提出一种新的概念来诠释这个矛盾.这似乎有点巧合,但实际上是人类科学技术的发展使然.
另外值得一提的是,在物理学发展史上,其实早就有人提出过类似于电子素的概念,而且这个概念的历史看来几乎与量子力学本身一样长.比如,薛定谔(Schrödinger)[2]、马 德 伦(Madelung)[3]和 多 林(Döring)[4]等人曾分别于1926,1927和1976年对此进行过探讨,并且称之为马德伦流体(Madelung fluid)或电子物质(electron matter).只不过他们因当时科学发展水平和技术条件所限而未能深入研究下去而已.
之前,国内一些出版物[5-6]中曾将electronium一词译为“电素”.本文作者认为,应当将之更改为“电子素”,因为不仅从这个术语的构词,而且从那些物理学大师和前辈们的原意(他们明确指出,电子是由一种分布在原子壳层内的物质所组成的,这种物质可称为“电子物质或电子流体”)来看,它都是一个只直接与电子相关,而并不涉及原子核的概念.此外,电有正、负之分,而电子素实际上只带负电荷,因此电子素这个名称显然要比电素更加准确、贴切.
5 结束语
本文所介绍的电子素模型具有显著的创新特色.由于它将抽象的概率密度处理为具体的“物质”密度,因此不仅易于为广大师生和研究人员所接受和理解,而且还大大增强了模型自身的可操作性.运用或操作这个模型,既可以得出一系列与事实相符的结果或结论,又能使我们对物理学发展史上的某些曲折和争议获得进一步的认识.因此,新模型具有继续深入研究和推广的价值.
致谢:上海理工大学理学院院长顾铮先教授和华东师范大学朱鋐雄教授为本文提供了不少宝贵意见,作者谨在此表示深切的感谢.
[1]Schiff L I.Quantummechanics [M ].New York:McGraw-Hill,1968.
[2]Schrödinger E.Quantisierung als eigenwertproblem[J].Annalen der Physik,1926,384(4):361-376.
[3]Madelung E.Quantentheorie in hydrodynamischer form[J].Zeitschrift für Physik,1927,40(3/4):322-326.
[4]Döring W.Atomphysik und quantenmechanik II.die allgemeinen gesetze [M ]. Berlin: Walter de Gruyter,1976.
[5]Herrmann F.KPK 中学物理(初中版)[M].上海:上海教育出版社,2007.
[6]Herrmann F.KPK 新物理教程(高中版)[M].上海:上海教育出版社,2010.
