一种低复杂度Turbo乘积码自适应Chase译码算法

党小宇 陶 静虞湘宾 杨鹏程

(南京航空航天大学电子信息工程学院 南京 210016)

1 引言

Turbo 乘积码(TPC)是由2维乘积码构成的串行级联码，它是在Turbo码的基础上发展而来的[1,2]，采用行列交织[3]，可以达到与随机交织同样的性能。上个世纪90年代，Pyndiah等人[4,5]在Chase算法的基础上进行修改，提出了TPC的软输入软输出迭代译码算法，这种译码方式采用了Chase译码器的软输出信息取代二进制硬判决信息[6]进行迭代译码，同时，Chase算法的软输出可以看作是对数似然比(LLR)对二进制判决信息的估计值。Chase算法是接近最大似然译码性能的一种次最优的、复杂度较低的译码算法。Chase算法可以分为Chase-I, Chase-II和Chase-III 3类，它们的主要区别是测试序列产生的方式和个数不同。其中， Chase-II是Chase-I和Chase-III算法在译码复杂度和译码性能两方面的折中，因此，Pyndiah选用基于 Chase-II的 TPC迭代译码算法。

在信道编译码中，如何降低译码复杂度[7]，提高译码效率[8,9]和译码性能[10]一直是一个实际问题，很多专家学者都在研究。虽然在1994年，Pyndiah等人[11,12]验证了新的分组 Turbo码可以在误码率性能和复杂度性能之间取得折中，但是在降低复杂度方面，仍然存在提升的空间。在文献[13]和文献[14]中，已经有报道了TPC自适应译码算法，它们在译码过程中，都需要估计SNR的值，根据SNR的估计结果，改变每次迭代码块中不可靠位数(LRB)的值。

本文提出了一种全新的自适应Chase迭代译码算法，其思想是统计译码过程中TPC码块每一行/列代数译码后的序列与接收序列的相同最小欧氏距离的个数，根据统计分析结果自适应地降低译码中最不可靠位数的值，从而成倍降低2p个测试序列的个数和相应的欧式距离求解计算量。与现有的Pyndiah每次迭代译码采用固定不可靠位数值p的算法相比较，本文提出的算法能在译码性能略有降低的代价下，显著减少了译码复杂度。

本文的内容安排如下：第2节，回顾TPC的编码方法和传统的Chase-II迭代译码方式；第3节，重点介绍自适应TPC译码的思想和步骤；第4节，给出不同门限值A的自适应 TPC误码率和复杂度曲线仿真结果，并且分析了其优越的性能；第5节，总结全文，给出结论。

2 TPC编译码方式

2.1 TPC编码原理

Turbo乘积码通常是由两到三个线性系统码组成的块状码。如图1所示，两个系统码和，其中分别表示信息位的数目、码长和最小汉明距离。TPC编码首先将个信息位排列在如图1位置的左上角，然后进行行编码得到矩阵，再进行列编码得到矩阵[15]。编码完成后的TPC码块表示为,C的参数如下，它最多可以纠正个随机错误，体现了TPC码很强的纠错能力。编码的时候，也可以先进行列编码，然后进行行编码，编码效果相同。在通信系统传输过程中，可以逐行传输，也可以逐列传输。通常为了降低编译码的实现复杂度，但又不影响性能分析，Turbo乘积码的两个系统码选择相同，即。

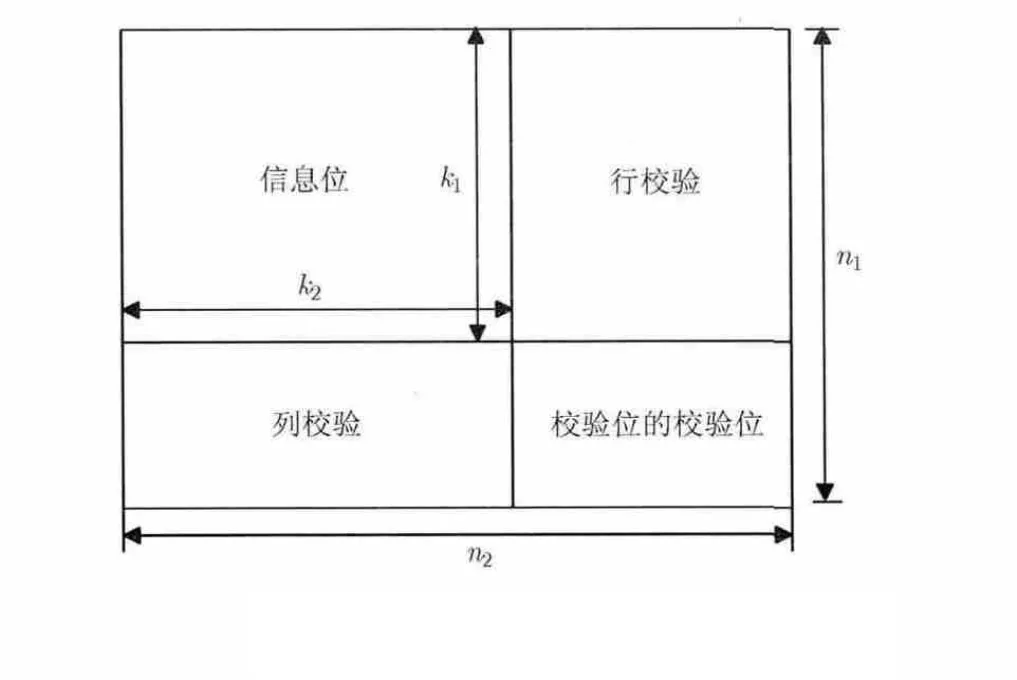
图1 TPC编码结构图

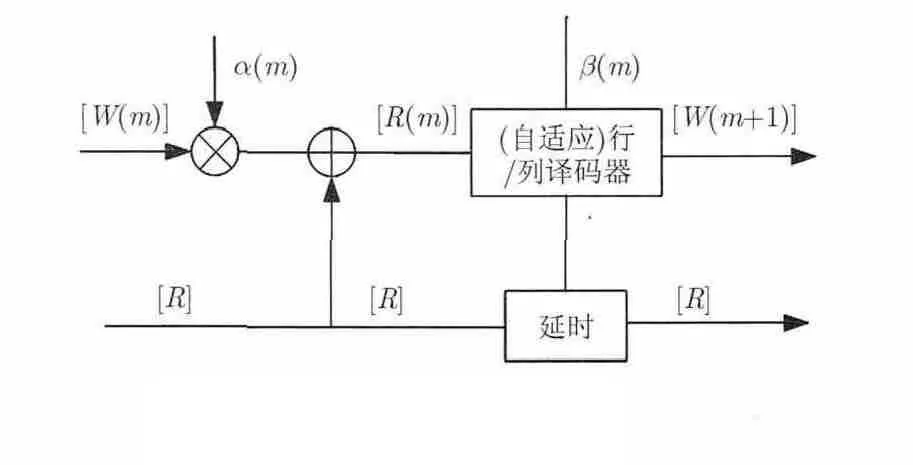
图2 TPC译码流程图

2.2 基于Chase-II的TPC译码原理

传统TPC译码一般采用Chase-II 迭代译码算法，它既可以用于行译码又可以用于列译码。基本原理是：对接收到的信号，利用硬判决译码器，根据不同的试探序列产生候选码字，然后把它们与接收序列对比，选择一个与接收序列有最小软距离的候选码字作为译码器的输出码字。

C的欧氏距离定义为

在迭代译码过程中，Chase译码器产生判决码字D和竞争码字B，用来计算软输出信息[()]R'm 和外信息 []W m，进而产生新的软输入信息 []R m作为下一次迭代的输入信息。其关系可表示如下：

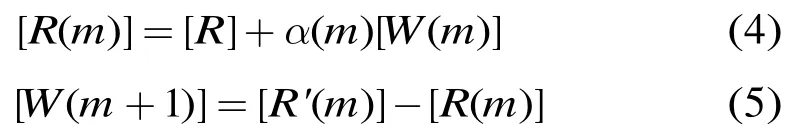
大量仿真和工程实践表明[4,5,11,12]，进行 4次迭代输出最后的判决码字可以达到比较理想的译码性能，同时也可以控制译码的复杂度。因此，为了统一比较标准，在后文的自适应译码仿真中均采用 4次迭代，并且该结果具有一般性。图2为TPC译码流程图，其中译码器复杂度与(自适应)行/列译码器模块密切相关，所以本文采用自适应译码来降低译码复杂度和延迟。是用来调整译码过程中不可靠外信息对译码造成影响的比例因数。当最佳译码序列找不到时，()mβ是预先定义的值，用来表示判决码字D的可靠性。

3 自适应TPC迭代译码算法

本文的自适应TPC译码算法是在Chase-II 迭代译码算法基础上，通过观察分析每次译码过程内部的规律，研究总结后提出的。

3.1 基于Chase II译码算法的结论

为了方便讨论，文中采用扩展汉明码作为TPC的子码，扩展汉明码可以纠正一个随机错误，同时发现两个随机错误。虽然本文的结论和推导证明是在此前提下得到的，但是只需要以此类推，便可以拓展到其它更为一般的子码。

在一个 TPC码块的一次迭代译码过程中，我们通常设定行/列译码的不可靠位数值p,可以产生2p个测试序列，经过代数译码后，产生2p个备选序列。接收序列R和备选序列的相应的欧氏距离记为，并且我们将欧氏距离集合中最小相同欧氏距离的序列个数用sN 来表示。

经过对 TPC码块接收序列错误发生在可靠位和非可靠位的深入分析推导，我们可以得到如下 3个重要的结论：

(1)在行(列)译码过程中，采用最不可靠位数p，可以产生2p个测试序列，经过代数译码后得到2p个备选序列。如果没有错误或者有一个错误发生在p个不可靠位中，则备选序列中存在个相同的序列，它们与接收序列的欧氏距离最小。

(2)如果有一个错误发生在除了p个最不可靠位的其它位，虽然概率比较小，备选序列中只存在一个序列，它与接收序列的欧氏距离最小。

由于篇幅所限，上述3个结论的证明略。

3.2 自适应TPC译码步骤

基于上述重要结论和证明，本文提出了一种全新的自适应TPC迭代译码算法，通过调整不可靠位数的值p来进行自适应Chase译码。

步骤1 对接收到的一个TPC码块进行第1次Chase-II行译码。采用不可靠位数p，每一行译码输出后得到该行软输入数据与代数译码后的序列的2p个欧氏距离。

步骤2 对步骤1中得到的2p个欧氏距离排序，记录下该行的sN 。等到一个码块的所有行译码结束后，统计这个码块中的行数rN，如果，则p值减1，进行第2次行译码；如果，则p值不变。具体门限值A取决于TPC子码的构造(下文仿真中给出A的取值)。

步骤 3 行列交织后对 TPC码块进行第 1次Chase-II列译码。列译码采用已经更新的不可靠位数值p进行译码，按照步骤 1的规则，统计一个码块中的列数，如果，则p值减1进行第2次列译码，如果，则p值不变。

步骤4 按照上述步骤1、步骤2、步骤3的规则进行第2次，第3次，第4次基于Chase-II块译码，并统计相同最小欧氏距离的个数sN ，不可靠位数p驱动下的自适应TPC迭代译码，输出最终译码结果。

图3给出了TPC一个码块在一次迭代过程中，自适应译码与传统Chase-II译码的对比流程图，图中虚线框为自适应TPC译码流程图，可以清楚看到本文自适应译码算法的步骤及其与传统译码算法的区别。上述3个重要的结论和步骤是自适应TPC译码的核心，后文将通过仿真实验验证其误码率和复杂度性能。

4 仿真分析

为了验证本文提出的自适应 TPC译码算法的性能，仿真中选择BPSK调制方式，通过加性高斯白噪声信道传输TPC编码后的信息。其中TPC子码采用相同扩展汉明码(128,120,4)进行行和列编码。

图4和图5分别给出了TPC2(128,120,4)的误码率和复杂度性能仿真曲线。文中的复杂度是指在迭代译码过程中，根据不同的测试序列产生备选序列，平均每个信息块需要采用的实数乘法运算(加法运算可忽略)的次数可以参考文献[9]。需要指出的是，为了方便比较，图5中纵坐标统一表示成归一化后的复杂度。它将标准的Chase-II译码算法4次迭代采用固定的不可靠位数的值计算出来的实数乘法数目，作为复杂度参考值，并归一化为单位 1，本文提出的自适应算法复杂度是在此基础上进行比较并且归一化得到的。

可以看出，误码率和复杂度性能将随着不同门限值A的变化而变化。当门限值A接近子码的长度时，误码率性能将和传统的每次迭代p为固定值的性能几乎相同，但是复杂度大幅度降低。当门限值A比较小时，虽然会损失一些误码性能，但是复杂度却可以更低。

图3 自适应TPC译码流程图

图4和图5中包含了5个不同的门限值 96,A=82,62,42,22，从这两幅仿真图可以清楚地看出性能曲线随着不同门限值的变化关系。例如，当 96 A=时，在误码率处，自适应算法相比传统译码算法每次迭代采用固定不可靠位数的值p，只损失了0.08 dB的性能，但是平均复杂度降低了约40.4%；当 22A= 时，在误码率处，自适应译码的误码性能也只有近0.3 dB的损失，但是平均译码复杂度只有传统译码的64%，约1/3。因此，我们可以选择不同的门限值来满足实际应用需要，在复杂度和误码率性能之间寻求折中。

图4 不同门限值下的TPC误码性能曲线

5 结论

图5 自适应TPC复杂度性能曲线

本文提出了一种全新的低复杂度自适应 TPC迭代译码算法，并且通过仿真验证了本文算法的正确性和可行性。与传统迭代译码采用不可靠位数p为固定值的Chase-II迭代译码算法相比，当采用编码效率为0.879的扩展汉明码时，在误码率为处仅损失约0.08 dB的性能，但是译码平均复杂度可降低约2/5，适用于通信译码实时性需求较高的场合。

[1] 詹明, 周亮. 一种基于对称性的双向双二进制卷积Turbo码译码结构研究[J]. 电子与信息学报, 2012, 34(5): 1179-1184.Zhan Ming and Zhou Liang. A bidireotional decoding architecture for double binary convolutional Turbo code based on symmetry[J]. Journal of Electronic ＆amp; Information Technology, 2012, 34(5): 1179-1184.

[2] 戴利云, 杨鸿文, 尧文元. 改进的Turbo类编码的近似码字错误率公式[J]. 电子与信息学报, 2012, 34(5): 1191-1195.Dai Li-yun, Yang Hong-wen and Rao Wen-yuan. An improved approximate formular for word error rate of Turbo-like codes[J]. Journal of Electronic ＆amp; Information Technology, 2012, 34(5): 1191-1195.

[3] Fonseka J P, Dowling E M, Brown T K, et al.. Constrained interleaving of Turbo product codes[J]. IEEE Communications Letters, 2012, 16(9): 1365-1368.

[4] Pyndiah R, Glavieux A, Picart A, et al.. Near optimum decoding of products codes[C]. IEEE Global Communications Conference, San Francisco, CA, 1994: 339-343.

[5] Pyndiah R. Near-optimum decoding of product codes: block Turbo codes[J]. IEEE Transactions on Communications,1998, 46(8): 1003-1010.

[6] Chase D. Class of algorithms for decoding block codes with channel measurement information[J]. IEEE Transactions on Information Theory, 1972, 18(1): 170-182.

[7] 柳昭, 魏延清, 张晓明. Turbo乘积码译码算法的优化和改进[J]. 计算机应用, 2013, 33(2): 397-399.Liu Zhao, Wei Yan-qing, and Zhang Xiao-ming.Optimization and improvement for Turbo product code decoding algorithm[J]. Journal of Computer Applications,2013, 33(2): 397-399.

[8] Morero D A and Hueda M R . Efficient concatenated coding schemes for error floor reduction of LDPC and turbo product codes[C]. IEEE Global Communications Conference,Anacheim CA, 2012: 2361-2366.

[9] Dave S, Kim J, and Kwatra S C. An efficient decoding algorithm for block turbo codes[J]. IEEE Transactions on Communications, 2001, 49(1): 41-46.

[10] Chen Guo-tai, Cao Lei, and Zheng Hai-feng.Near-Log-MAP decoding for turbo product codes[C].International Conference on Wireless Communications,Networking and Mobile Computing (WiCOM), Wuhan, 2011:1-4.

[11] Pyndiah R. Iterative decoding of product codes: block turbo codes[C]. IEEE International Symposium on Turbo Codes＆amp; Related Topics, Brest, France, 1997: 71-79.

[12] Pyndiah R, Picart A, and Glavieux A. Performance of block turbo coded 16-QAM and 64-QAM modulations[C]. IEEE Global Communications Conference, Singapore, 1995, 2:1039-1043.

[13] Mahran A and Benaissa M. Adaptive Chase algorithm for block turbo codes[J]. Electronic Letters, 2003, 39(7): 617-619.

[14] Liu Xing-cheng, Zhang Wei, Wang Zhong-feng, et al.. An efficient adaptive decoding for block turbo codes[C].International Conference on Wireless Communications,Networking and Mobile Computing (WiCOM), Wuhan, 2006:1-5.

[15] Adde P, Pyndiah R, Raoul O, et al.. Block turbo decoder design[C]. IEEE International Symposium on Turbo Codes ＆amp;Related Topics, Brest, France, 1997: 166-169.

[16] Goalic A and Pyndiah R. Real-time turbo-decoding of product codes on a digital signal processor[C]. IEEE International Symposium on Turbo Codes ＆amp; Related Topics,Brest, France, 1997, 2: 624-628.