RFID多读写器自适应加权功率分配算法

王 帅李书芳

(北京邮电大学信息与通信工程学院 北京 100876)

1 引言

有效抑制RFID读写器间的干扰是RFID技术应用中亟待解决的重要技术问题之一。当有限空间内分布大量RFID读写器时，即使读写器识别范围未发生重叠，由于到达读写器端的标签散射信号比较微弱，仍易受到来自其它读写器信号的干扰而导致信噪比降低，从而使其标称识别半径减小。

针对读写器干扰问题，学界已开展了大量研究，早期研究如 HiQ[1]等多将重点放在减少读写器信号的碰撞概率方面，这些算法的缺陷在于将碰撞的结果简单归结为读取失败，但该假设已被后期的一些实验结果证明并不严谨。文献[2]基于近期的实验结果，认为读写器间即使产生碰撞也只会降低各自的信噪比，识别半径相应减少但一般不会减至零，继而提出了读写器间干扰的统计模型，以及与读写器数量、功率、信道数有关的信噪比表达式。但该文献认为各读写器功率相等，且位置呈均匀分布，这对实际应用来说只是一种理想假设。文献[3-5]对多读写器的干扰模型进行了研究，分析了读写器在干扰环境下的读写距离，给出了路径损耗因子、信噪比和噪声功率等参数对干扰模型的影响大小。文献[6]提出了一种分布式功率分配方案，该方案根据识别距离的期望值，通过检测信噪比不断更新发射功率。文献[7]提出通过检测接收信号强度的方法实时调整发射功率。算法收到标签返回的信号后，先根据其 RSSI(Received Signal Strength Indication)值估计出读写器和标签间的距离，然后根据所估计的距离将发射功率调整到合适的数值。文献[8]根据检测到的信噪比，采用具有回退功能的功率控制算法调整发射功率。与文献[6]相比，该算法通过引入回退功能，有效避免了因各读写器贪婪增大功率导致的功率“死锁”(各个读写器功率已达到最大值，但仍在试图增大功率以致陷入死锁)的情况。上述功率控制算法虽然在一定程度上起到了抑制读写器间干扰的作用，但本质上都属于启发式算法，难以实现多读写器识别性能的全局优化和公平性。

本文分析了在读写器位置随机分布条件下如何分配功率以最大程度抑制读写器间干扰的问题，首先提出了信噪比估计式，并对估计式的性能进行了评估；根据RFID系统的应用需求，将读写器功率分配定义为自适应加权公平问题，并从理论上证明了该问题可以等价为求解指定效用函数的加权优化问题；为使算法在实际应用中更易于实现，设计了分布式功率更新算法，并对其收敛性进行了证明。

2 多读写器应用系统模型

以文献[2]的读写器干扰模型为基础，本文研究的多读写器系统应用场景如图1所示，在半径为D的区域内随机分布若干个读写器，每个读写器功率均可调，且作如下假设和条件设定：

图1 多读写器干扰模型

(1)读写器间距离d大于最小距离 rmin,rmin的设定以保证读写器识别范围不发生重叠为原则，避免标签端读写器碰撞的情形发生。

(2)路径损耗与dγ成比例，其中γ设为2.5。

(3)读写器干扰为非相干的加性干扰，即多读写器对于某位置的干扰等同于单个读写器干扰的叠加。

(4)读写器具有两个状态：活动状态和非活动状态，处于活动状态的概率为，读写器只有处于活动状态时才会产生干扰。

(5)读写器采用跳频通信模式，每次所用信道可在50个信道中随机选择。

(6)每个读写器的标称读写半径均为 Rnom，通过调节发射功率，实际读写半径可以大于或小于Rnom。

读写器周期性发出查询命令，识别处于标称识别半径内(如图 1虚线所示)的标签。当工作区域内读写器数量增加，干扰程度加大时，实际可识别半径 Rreal将低于标称值，可通过合理调节每个读写器的发射功率抑制读写半径的下降。

3 误包率与信噪比估计

3.1 误包率估计

在功率控制算法设计中，设备接收端的信噪比是十分重要的参数，功控算法一般要根据检测到的信噪比和其它参数进行计算和控制。获取信噪比除了硬件测量的方式，也可通过接收数据误包率间接得出，而且，当设备不具备信噪比检测功能时采用这种方法更为实用，因为不用额外增加检测硬件。

读写器与标签间通信采用 TDMA帧时隙方式，每一帧被划分为若干个时隙，读写器通过帧头发出查询命令后，每个标签任意选择一个时隙发送数据，每个时隙有 3种可能状态：空闲(无标签)、成功(仅一个标签)和碰撞(两个或以上标签)[912]-。设当前帧长(即时隙数量)为L，检测到空闲时隙、成功时隙和碰撞时隙的个数分别为1X,2X,3X。由于噪声和干扰的存在，数据包即使未发生碰撞也可能出现接收错误，导致一些成功时隙转化成碰撞时隙(无法正确解码，等同于多标签碰撞的情况)，将处于该时隙的数据包称为错误包。设a为错误包个数，则真正的成功时隙和碰撞时隙的个数应为和。对于每一帧，不同类型的时隙个数组成向量，对应的期望值组成向量，其中和可根据文献[13-15]由式(1)-式(3)给出：

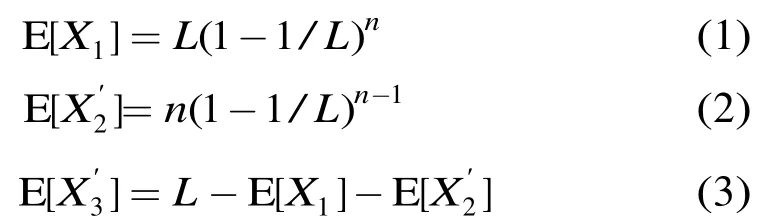
式中n为标签数量。实际中无法获得n和a的真实值，但n和a越接近真实值，观测向量和期望向量E[X']间的相似程度就越高。根据模式识别理论，可以用欧式距离的方法衡量两个向量的相似程度，即寻找使X'与E[X']的欧式距离最小的n和a作为估计值：

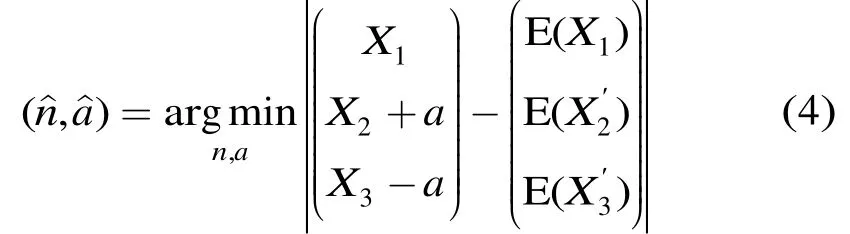
定义 1 已知错误包个数a，设误包率真值为pe，定义误包率估计子为

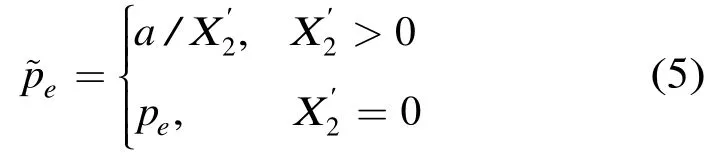
下面分析该估计子的统计特性。

定理 1 令sp表示时隙为成功状态的概率，设各成功时隙误包与否相互独立，则按式(5)定义的误包率估计式为无偏估计。

证明

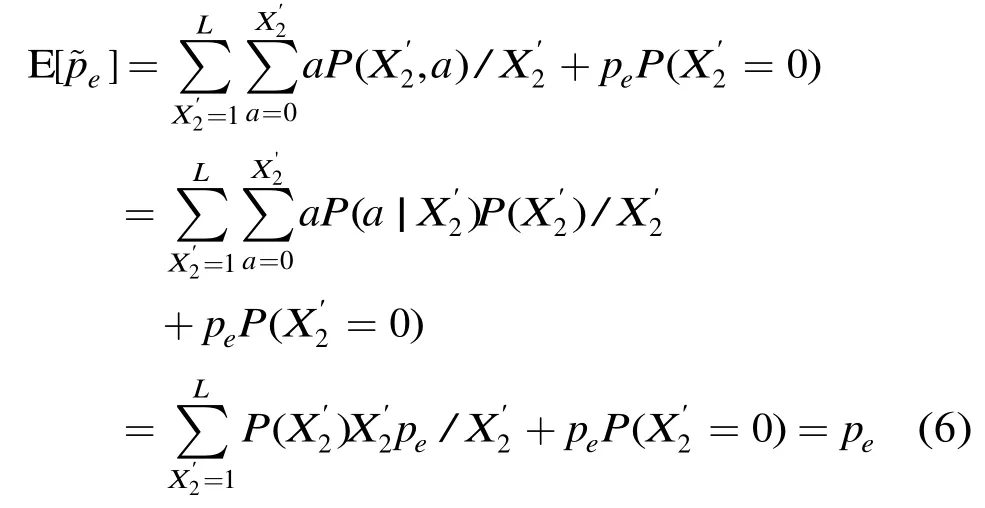
因此，式(5)定义的估计式无偏。 证毕

3.2 信噪比计算

标签信号采用 ASK调制，读写器接收端误比特率为

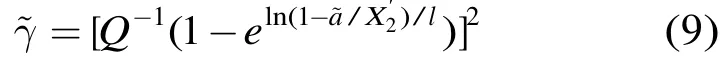
4 功率分配算法

4.1 问题建模

本文研究在多读写器环境下如何通过调节各自的功率以保证各读写器性能(读写半径或接收信噪比)均能保持在标称值附近的问题。提出自适应加权功率分配算法，基本思想是在比例公平算法的基础上，增加自适应权重因子，当某读写器性能趋向低于标称值时，其权重值自动增大，引导资源更多地分配给该读写器。以文献[16]中比例公平问题定义为基础，将本文的问题建模为自适应比例公平问题。

定义 2 向量*x称为自适应比例公平解，如果其为可行解并且对于任意向量x，则式(10)成立

4.2 问题求解

可以将定义2的问题转化为最优化问题以方便求解。考虑式(11)的最优化问题：

其中。

证明 先证充分性。令*x为问题式(11)的解，通过计算可得到

由式(14)和式(15)可知问题式(11)的汉森矩阵负定，因此目标函数式(11)是严格凸函数，存在唯一的最优解。设λ为待定系数，令

问题式(11)最优解*x的Karush-Kuhn-Tucker(KKT)条件为

4.3 分布式功控算法

用读写器信噪比取代问题式(11)中的自变量x，可得到读写器功率控制问题的最终形式：

问题式(21)对于向量P是非凸问题，一般来说求解较为困难。本文采用分布式算法简化运算，其基本思想是将问题式(21)的全局求解问题转化为分布式的局部优化问题，每个读写器利用式(21)只更新自己的功率值。为了减轻信道负荷，每个读写器采用第3节中的方法，周期性地估计当前的信噪比并与标称值比较，只有当信噪比低于标称值时才向外发送功率更新请求及自己的功率值，启动更新过程。以下是分布式算法的具体步骤(不失一般性，设算法运行在读写器s上)：

(1)初始化。将发射功率sP调整为预设值(默认设置在标称值附近)，启动读写器工作；

(2)标签识别和时隙状态采集。发出标签识别命令 query，在标签响应帧中收集空闲、成功和碰撞的时隙个数，用式(9)计算和更新信噪比的估计值；

(3)功率控制。根据信噪比的大小选择相应的控制策略：

上述分布式算法涉及到两个问题：一是算法是否收敛，二是如果收敛，其收敛点是否为问题式(21)的局部最优解。下面围绕这两个问题展开讨论。

不失一般性，考虑读写器s的局部优化问题。

定理 3 对于读写器s，问题式(22)是凸优化问题。

证明 对于读写器s，将式(22)重写为

证毕

每个读写器通过求解式(22)的局部目标函数更新自己的功率值，相应地，式(21)的全局目标函数的值也随之变化。令 ()L t为t时刻式(21)的值，则有：

定理 4 (1)分布式更新算法收敛，即存在*L:；(2)设算法在处取得，则,都不会被更新，且为问题式(21)的KKT点。

证明

5 仿真结果

将本文方案与3个方案进行对比，分别是文献[2]中基于均匀分布假设的固定功率分配方案，文献[16]中的比例公平功率分配方案，以及文献[8]中的功率可回退控制方案 BKPC(BacKoff Power Control)，在比例公平功率分配方案中采用与式(21)类似的形式，并使用相同的效用函数，只是令恒为1。仿真参数按第2节中相应数据设置。

首先将最小信噪比作为衡量算法公平性的指标。从图2可看出随着用户数的增加，读写器间距在不断缩小，相互之间干扰也随之加大，最小信噪比随着用户数的增加有降低的趋势。均匀分布假设下的功率固定分配算法根据工作区域大小和读写器密度参数，功率分配的公平性较差，最小信噪比最低。功率可回退控制方案根据信噪比调节输出功率，性能要好于固定分配方案。比例公平算法考虑了功率分配的公平性，最小信噪比要大于均匀分配算法和功率可回退控制方案，但采用该算法当读写器密度很大时，仍会发生个别读写器信噪比远小于标准信噪比的情况。本文提出的自适应加权算法基于比例公平算法，同时对处于高密度区域的读写器自动增加权重，使处于严重干扰区域下的读写器仍能尽量保证一定的信噪比，最小信噪比高于其它 3种算法。

读写器信噪比标准差是衡量算法公平性的另一个指标。如图3所示，固定功率分配算法以读写器位置均匀分布为假设，不考虑干扰程度随位置变化的因素，方差最大。功率可回退控制方案采用启发式算法，通过回退仅能实现有限的全局优化能力，信噪比仍有较大的方差。比例公平算法将读写器位置信息考虑在内，公平性要比均匀分配和功率回退算法好。本文提出的自适应加权算法除了具有比例公平算法的优点外，还可以根据读写器所处环境状况自动调节权重因子，最大程度地减小读写器密度分布差异对功率分配公平性的影响，方差要低于上述3种算法。

在多读写器应用场景中，各读写器由于所受干扰不同，其数据吞吐量也各不相同。图4显示了多读写器中平均吞吐量的数值和趋势比较，通信数率设为100 bit/s。由图可见，当读写器个数增加时，4种算法的最小吞吐量都逐渐减小，且当数量较多时趋于某固定数值，说明4种功率控制算法都只能在一定读写器数量下发挥作用。由图可见，自适应加权算法性能始终优于其它3种算法，其吞吐量随读写器数量增多而下降的速度也最为缓慢。

图5显示了本文提出的分布式算法收敛性能，给出了分布式算法求得的局部最优解与全局最优解的相对误差，并与等比例分配和BKPC算法的收敛性做了比较。从图中可以看出，随着迭代次数的增加，自适应加权算法的迭代值稳定地收敛，且与全局最优解的相对误差逐渐减小，当迭代次数大于150时，相对误差可控制在3%以内，说明该分布式算法具有良好的收敛性能，且尽管求出的是局部最优解，但满足一定的迭代次数后非常接近全局最优解。等比例分配由于算法流程与自适应加权相同，因此具有相近的收敛特性。BKPC算法基于启发式调整策略，在迭代过程中迭代值波动幅度较大，收敛的速度最慢，当迭代次数大于200时才能稳定地使误差控制在3%以内。

图6比较了算法在时间复杂度方面的性能，其中BKPC，等比例分配，自适应分配方案中更新周期设为0.1 s, BKPC中的回退周期设为0.1~0.5 s。由图中可以看出，由于等比例分配和自适应分配方案的收敛迭代次数小于BKPC算法，达到收敛值消耗的时间也明显少于BKPC。

以上比较了固定场景的算法性能，下面考察移动环境下，即区域内读写器数量和位置发生变化时的性能。图7所示为读写器位置和数量每隔30 s变化一次，其中位置做随机变化，数量变化的方式做如下设定：(1)0~29 s内有 40个读写器共存；(2)30~59 s内新加入 20个读写器，共有 60个；(3)60~89 s内又加入 20个读写器，共有 80个；(4)90 ~120 s内又加入20个读写器，共有100个；(5)120 ~150 s内20个读写器离开，总数恢复到80个。将固定算法分配方案中读写器数量参数设为 70个(因图7平均数量约为70)，BKPC，等比例分配，自适应分配方案中更新周期设为0.1 s, BKPC中的回退周期设为0.1~0.5 s。由图6可看出，当读写器由于移动而使区域内数量改变时，自适应功率分配算法可以很快收敛到最优值(9 s以内)，而且最小吞吐量始终高于其它3种算法，说明算法在移动场景下具有较好的适应能力。

图2 4种方法的最小信噪比

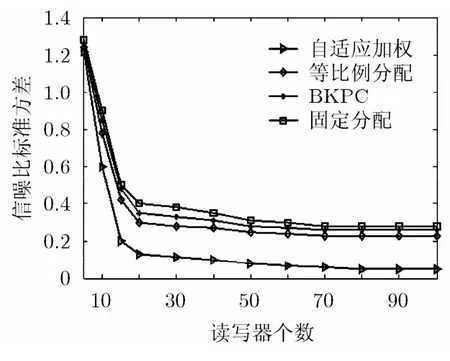
图3 4种方法的信噪比标准方差

图4 4种方法的平均吞吐量比较

图5 3种方法的分布式算法收敛性能

图6 3种算法的时间复杂度比较

图7 4种功控算法的实时性能

6 结束语

读写器间干扰是多读写器应用场景中面临的主要问题。本文提出的自适应权重功率分配算法对低于标称信噪比的读写器自动增加权重因子，使处于不同位置，所受干扰程度不同的读写器识别质量均能尽量接近标称值，满足RFID系统在应用中的实际需求，提出的分布式实现方法进一步提高了算法的实用性。仿真表明，算法在公平性和收敛性方面均表现出良好的性能，是解决RFID读写器干扰问题的有效方法。

[1] Ho J, Engels W, and Sarma S. HiQ: a hierarchical Q-learning algorithm to solve the reader collision problem[C].Proceedings of 2006 International Symposium on Applications and the Internet Workshops, Phoenix, 2006: 88-91.

[2] Kim Do-Yun, Yoon Hyun-Goo, and Jang Byung-Jun. Effects of reader-to-reader interference on the UHF RFID interrogation range[J]. IEEE Transactions on Industrial Electronics, 2009, 56(7): 2337-2346.

[3] Zhang Lin-chao, Ferrero Renato, and Gandino Filippo.Evaluation of single and additive interference models for RFID collisions[J]. Mathematical and Computer Modelling,2013, 52(3): 901-909.

[4] Yojima Hiroyuki, Tanaka Yu, and Umeda Yohtaro. Analysis of read range for UHF passive RFID tags in close proximity with dynamic impedance measurement of tag ICs[C]. IEEE Radio and Wireless Week, Phoenix, 2011: 110-113.

[5] Zhang Lin-chao, Ferrero Renato, and Gandino Filippo. A comparison between single and additive contribution in RFID reader-to-reader interference models[C]. Proceedings of 6th International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing, Palermo, 2012: 177-184.

[6] Dai Hongyue. Research on the distributed power control algorithm for RFID readers[C]. 2010 6th International Conference on Wireless Communications, Networking and Mobile Computing, Chengdu, 2010: 1-4.

[7] Boaventura A S and Carvalho N B. A proposal for dynamic power control in RFID and passive sensor systems based on RSSI[C]. Proceedings of 6th European Conference on Antennas and Propagation, Prague, 2011: 3473-3475.

[8] Wu Li-ming, Chen Tai-wai, and Xiang Ying. RFID anticollision for internet of things based on power control and backoff algorithm[J]. International Journal of Advancements in Computing Technology, 2012, 4(22): 560-566.

[9] Zhen B, Kobayashi M, and Shimizu M. Framed Aloha for multiple RFID objects identi?cation[J]. IEICETransactions on Communications, 2005, 57(8): 991-999.

[10] Kodialam M and Nandagopal T. Fast and reliable estimation schemesin RFID systems[C]. Proceedings of the Annual International Conference on Mobile Computing and Networking, California, 2006: 322-333.

[11] Harald Vogt. Efficient object identification with passive RFID tags[C]. Pervasive Computing, Zürich, Switzerland,2002: 98-113.

[12] Yu Zeng and Yuan Tan. A low-complexity tag number estimate in EFSA protocol for RFID tag anti-collision[J].Lecture Notes in Electrical Engineering, 2011, 102(3):495-502.

[13] Zhou Lin, Li Zhen, and Chen Ying-mei. The research on electronic tag quantity estimate arithmetic based on probability statistics[J]. Communications in Computer and Information Science, 2012, 59(4): 254-261.

[14] Liu Jing and Wu Hai-feng. The tag estimation and frame length determination with capture effect in dynamic frame slotted ALOHA about RFID[J]. Advances in Intelligent and Soft Computing, 2012, 32(6): 117-123.

[15] Deng Der-jiunn. Optimal dynamic framed slotted ALOHA based anti-collision algorithm for RFID systems[J]. Wireless Personal Communications, 2011, 59(1): 109-122.

[16] Kelly Frank. Charging and rate control for elastic traffic[J]. European Transactions on Telecommunications, 1997,8(1): 33-37.